【排序篇3】快速排序、归并排序
目录
- 一、快速排序
- 1.1 递归
- 1.2 非递归
- 二、归并排序
- 2.1 递归
- 2.2 非递归
一、快速排序
1.1 递归
快速排序的递归采用二叉树的前序遍历的思路,单趟排序先确定好一个元素的位置,然后往后递归再确定其他子区域内的某个元素的位置,直到只有一个元素返回。
递归的图示:
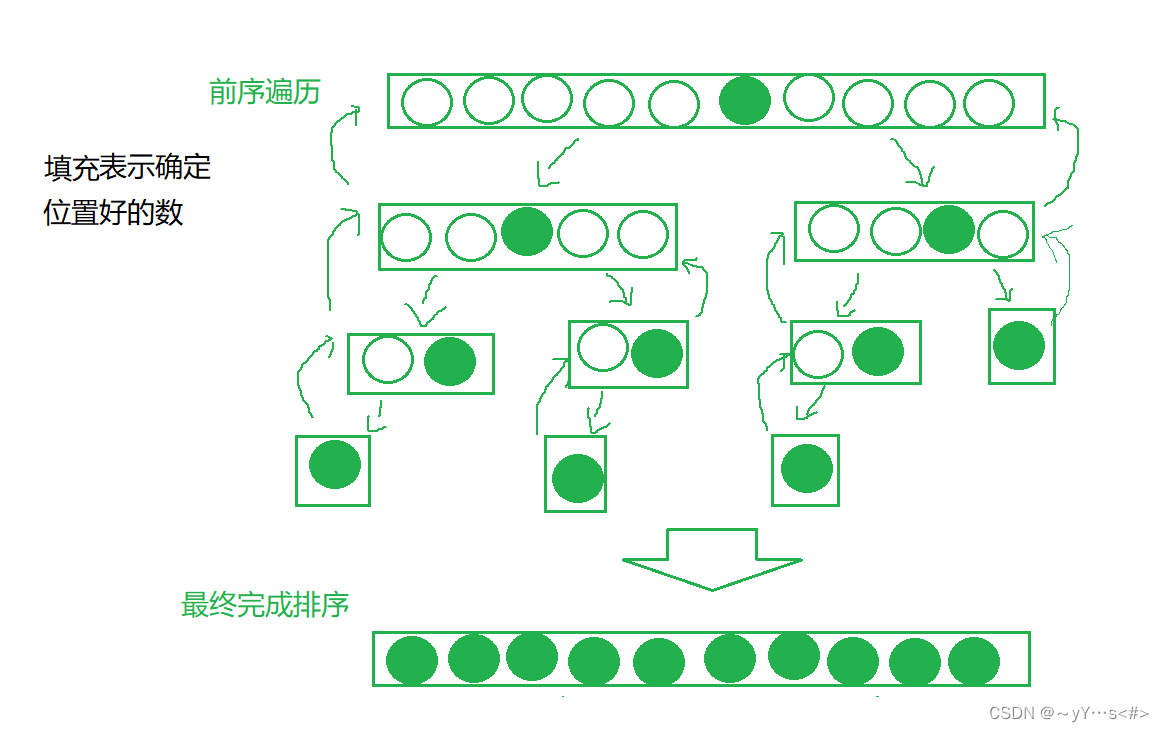
代码:
void QuickSort(int* a, int begin, int end)
{//区间内小于等于1,就返回if (begin >= end){return;}//单趟排序,返回确定位置好的元素下标int ki = partsort1(a, begin, end);//递归 - 区间:[begin, ki-1],[ki+1, end]QuickSort(a, begin, ki - 1);QuickSort(a, ki + 1, end);
}
接下来分析单趟排序的实现。有3种方式:Hoare法、挖坑法、前后指针法。
1️⃣Hoare法
整体思路:
- 通过三数取中获取较靠中间元素的下标mid,然后mid指向的元素与左端的元素进行交换,防止极端情况
- 定义一个变量 ki = left 便于记录左端的值,注意ki是下标
- 先移动右边再移动左边,right指向的元素大于等于ki指向的元素就减1往前走,小于就停下;left指向的元素小于等于ki指向的元素就+1往后走,大于就停下,然后两者停下分别指向的元素进行交换,然后先走右再走左继续移动
- left与right相遇,跳出循环,交换ki指向的元素和left指向的元素,此时left指向的元素就是确定好位置的元素,最后返回下标left
图示:
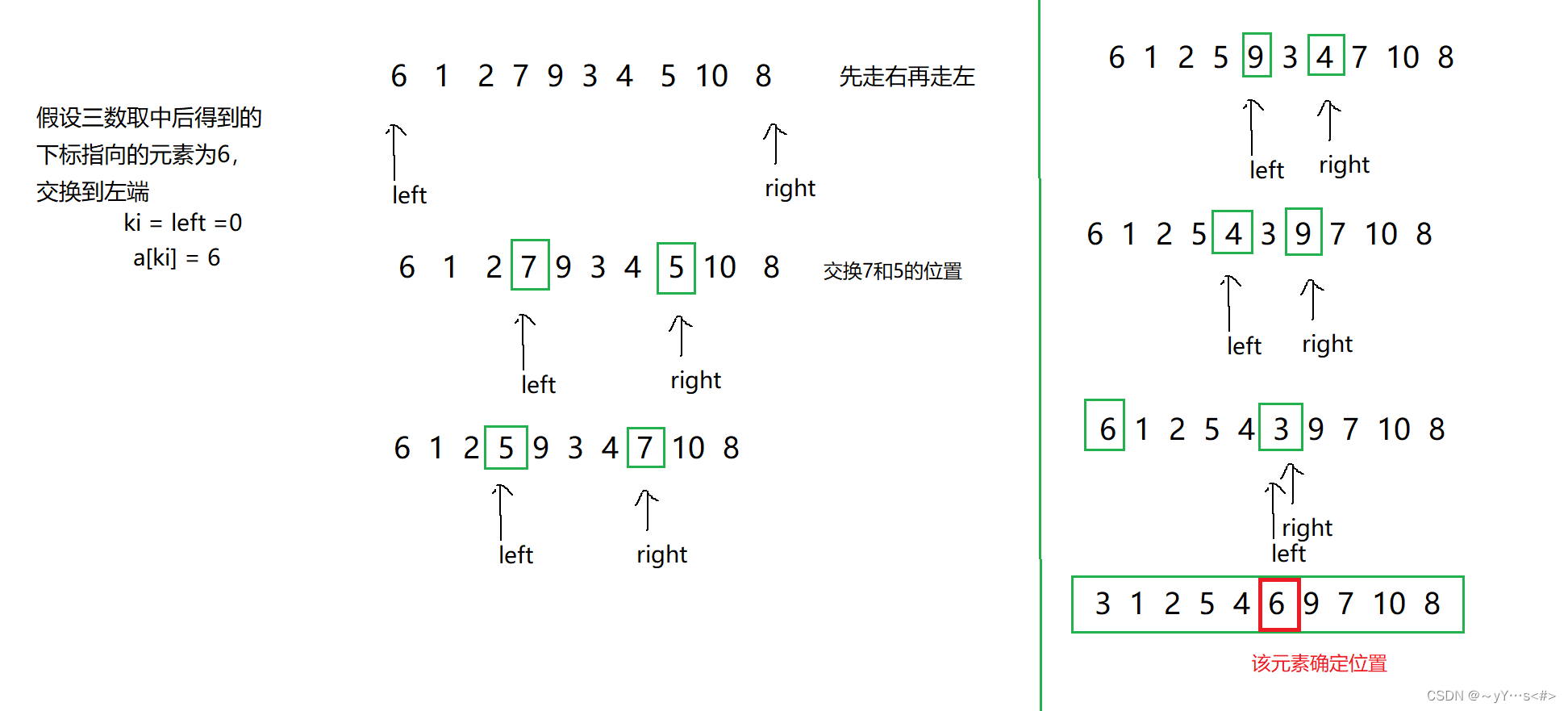
代码:
//Hoare法
int partsort1(int* a, int left, int right)
{//获取较中间的元素的下标int mid = getmid(a, left, right);//三数取中Swap(&a[left], &a[mid]);//与左端交换,防止极端情况int ki = left;//注意ki得到的是下标while (left < right){//先走右再走左while (left < right && a[right] >= a[ki])//是大于等于往前走,小于就停下{ // 防止走的过程中越界right--;}while (left < right && a[left] <= a[ki])//是小于等于往前走,大于就停下{ // 防止走的过程中越界left++;}Swap(&a[left], &a[right]);//交换两个元素}Swap(&a[ki], &a[left]);//把ki指向的元素交换到它最终的位置return left;//返回确定位置的元素的下标
}
问题1:为什么要三数取中
因为三数取中可以防止出现极端情况,该极端情况指:ki指向的元素本来就应该放在左端,比如:
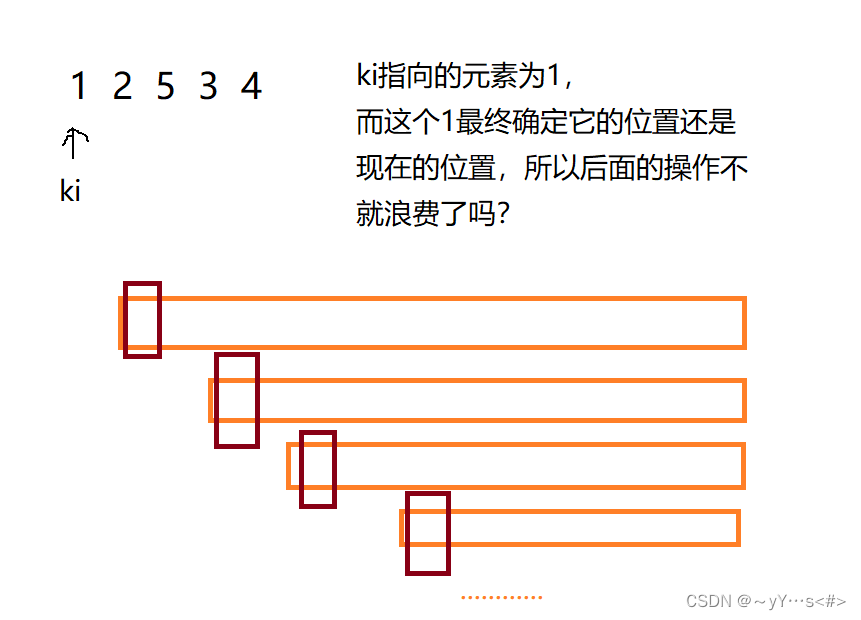
如果大部分是这种最坏情况,导致快速排序的复杂度为O(N ^ 2)
三数取中可以取到较靠中间位置的元素的下标,尽可能避免了以上情况,就算有个别还是在最左端,但是对整体的效率并没有多大影响。所以三数取中对快速排序的优化有很大的帮助。
代码:
//三数取中
int getmid(int* a, int left, int right)
{int mid = (left + right) / 2;if (a[left] < a[mid]){if (a[mid] < a[right])return mid;else if (a[right] < a[left])return left;elsereturn right;}else{if (a[mid] > a[right])return mid;else if (a[right] > a[left])return left;elsereturn right;}
}
问题2:为什么ki取的是下标,不是数组元素
这与最后确定元素位置的交换有关,假设ki是数组元素,交换的是left指向的元素和ki,那么结果是left指向的元素变成了ki这个元素,但是数组左端的元素依旧没变。

ki取的是下标,才能真正交换数组左端和left指向的元素。
问题3:为什么先走右边,再走左边
举个栗子:
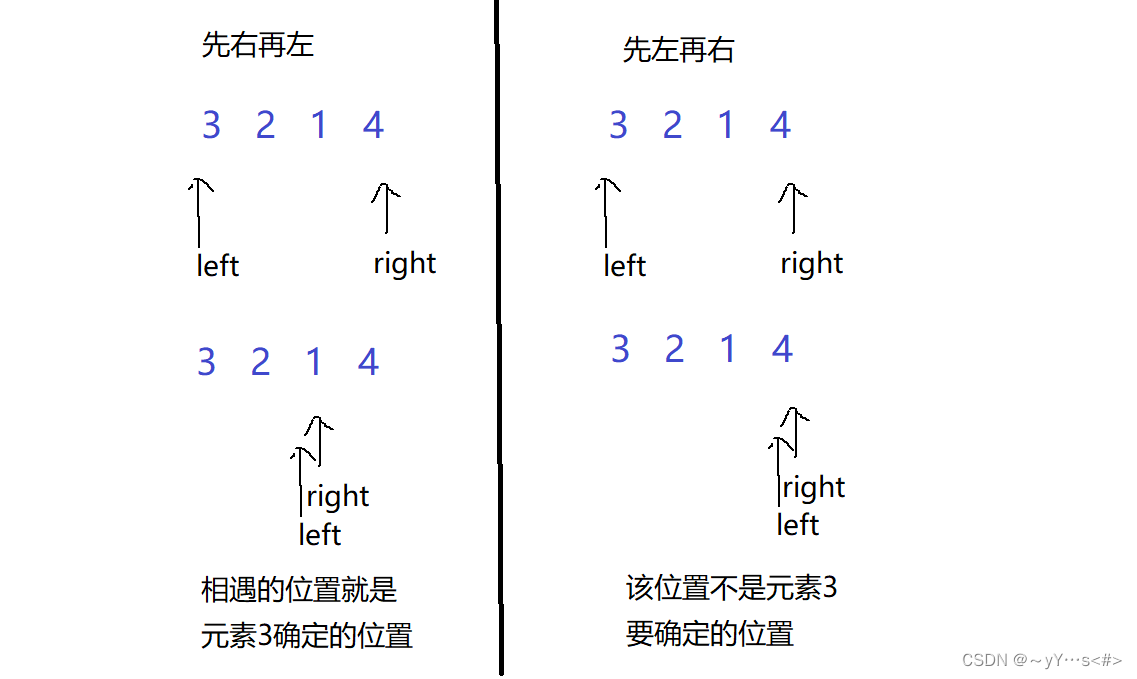
2️⃣挖坑法
整体思路:
- 三数取中,与Hoare法的步骤一样
- ki取的是left指向的元素,为后面的填坑作准备
- 定义一个坑hole = left (是下标)
- 先走右边,停下后,将此时right指向的元素覆盖坑位的元素,然后产生新的坑位,right变成坑
- 再走左边,停下后,将此时left指向的元素覆盖坑位的元素,然后产生新的坑位,left变成坑
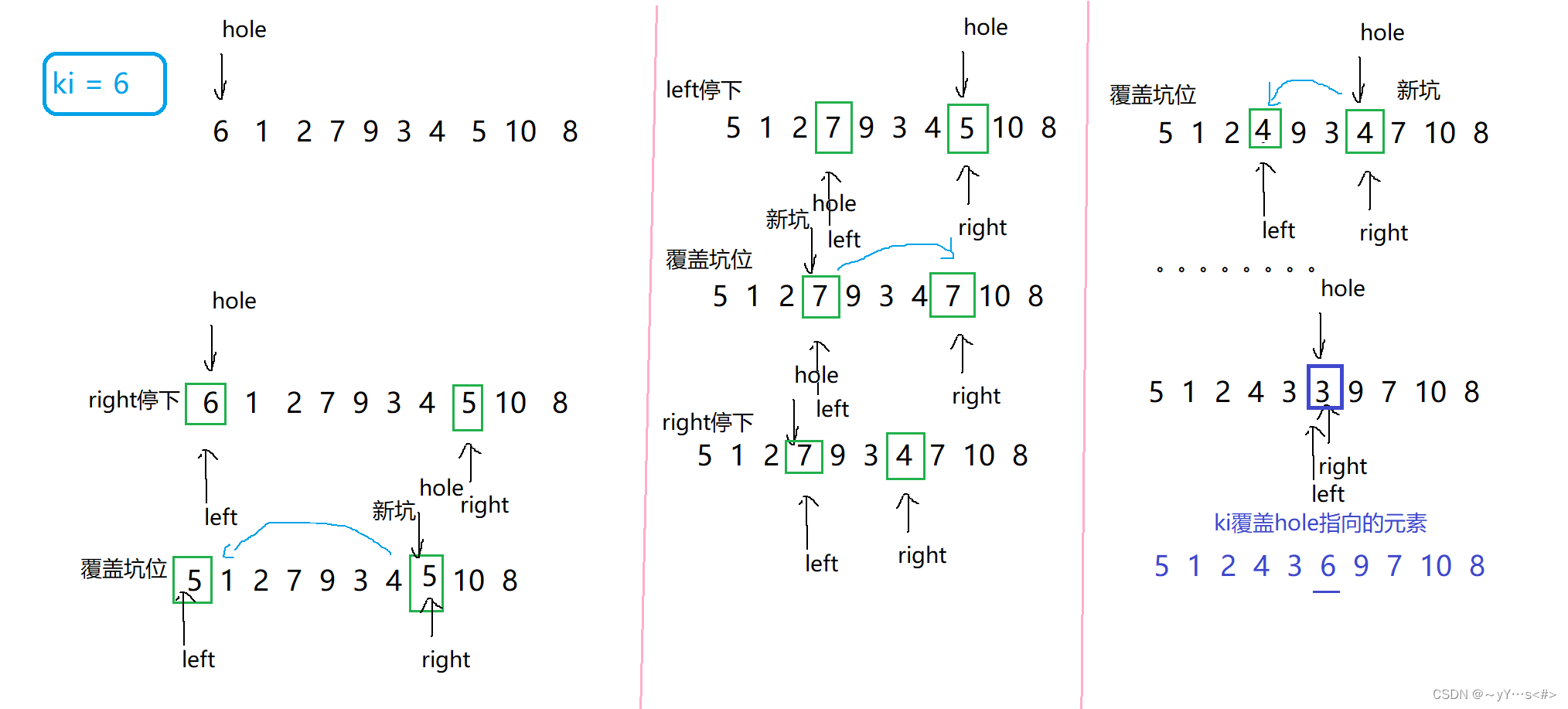
- 循环全部走完后,最终的hole就是ki要确定的位置,覆盖坑位,然后返回hole
图示:
代码:
//挖坑法
int partsort2(int* a, int left, int right)
{//获取较中间的元素的下标int mid = getmid(a, left, right);//三数取中Swap(&a[left], &a[mid]);//与左端交换,防止极端情况int ki = a[left];//注意ki得到的是数组元素int hole = left;//初始的坑的位置while (left < right){//先走右再走左while (left < right && a[right] >= ki)//是大于等于往前走,小于就停下{ // 防止走的过程中越界right--;}a[hole] = a[right];//覆盖坑位的元素hole = right;//产生新的坑位while (left < right && a[left] <= ki)//是小于等于往前走,大于就停下{ // 防止走的过程中越界left++;}a[hole] = a[left];//覆盖坑位的元素hole = left;//产生新的坑位}a[hole] = ki;//确定元素的位置return hole; //返回确定位置的元素的下标
}
3️⃣前后指针法
通过前面的两种方法可以发现:确定好某个元素的位置后,该元素的左右两个区间分别是小于这个元素和大于这个元素(以数组是1,2,3,4,5,6,7,8,9,10为例),也就是说要确定位置的元素是区分两个不同区间的标杆,所以这里可以使用前后指针法,用来区分两块区域。
整体思路:
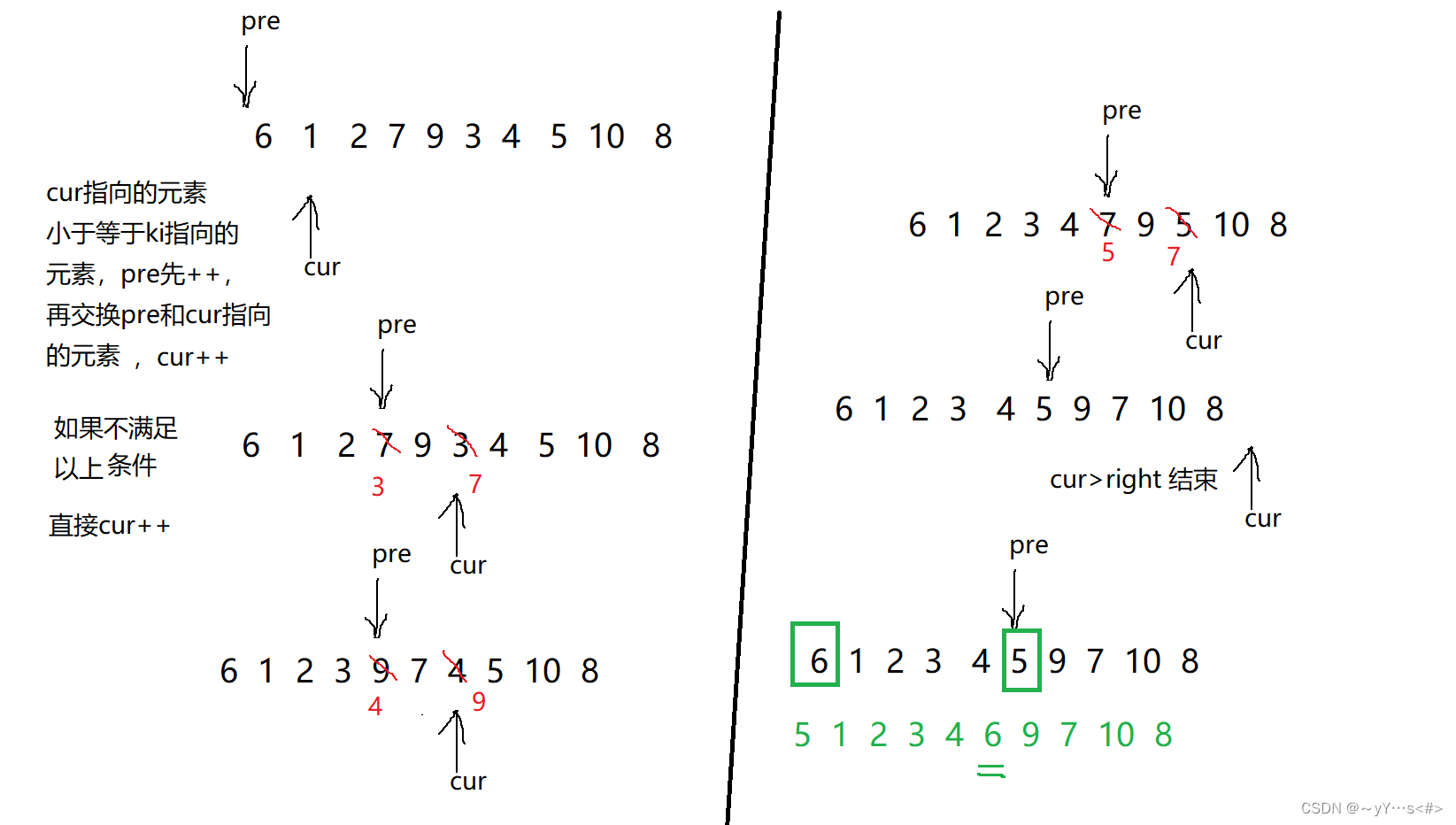
- 定义前后指针,cur=left+1,pre = left
- 如果cur指向的元素小于等于ki指向的元素,pre先加1,再交换pre和cur分别指向的元素,然后cur++
- cur循环完,交换pre和ki分别指向的元素,pre的位置就是确定好的位置,然后返回pre
图示:
代码:
//前后指针法
int partsort3(int* a, int left, int right)
{int mid = getmid(a, left, right);//三数取中Swap(&a[left], &a[mid]);//与左端交换,防止极端情况int ki = left;//注意ki得到的是下标int cur = left + 1, pre = left;//定义前后指针while (cur <= right)//范围限制{if (a[cur] <= a[ki])//如果小于,先++pre再交换分别指向的元素{Swap(&a[++pre], &a[cur]);}cur++;//cur都要往后走}Swap(&a[ki], &a[pre]);//把ki指向的元素交换到它最终的位置return pre;//返回确定位置的元素的下标
}
1.2 非递归
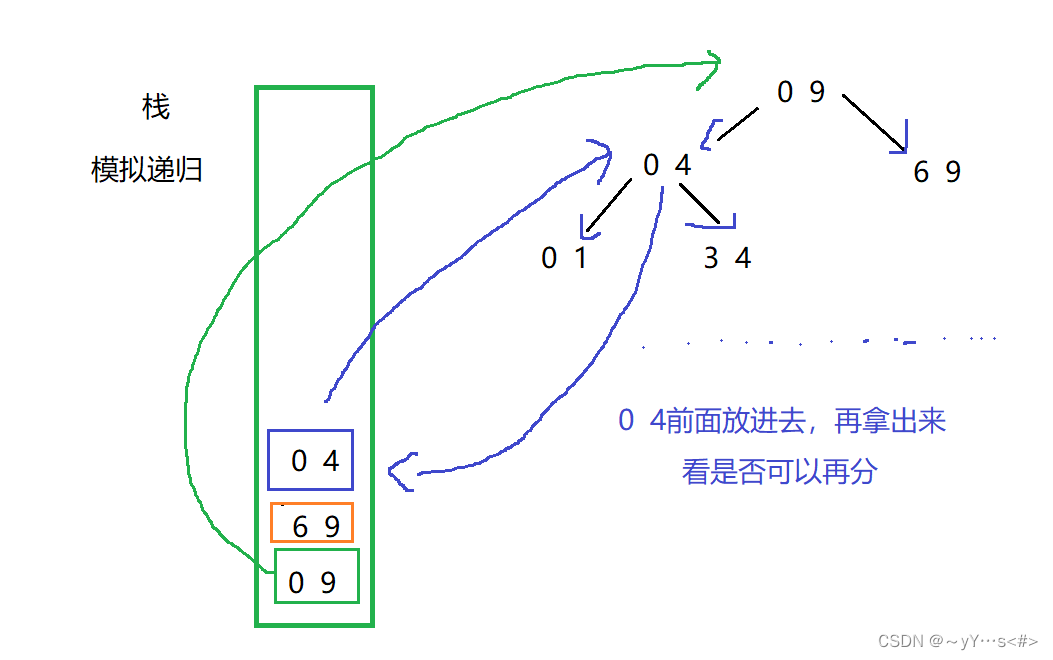
快速排序的非递归是用栈模拟递归来实现的,栈的特点是后进先出,递归是先左边再右边的,所以放入栈的数据应该先放右再放左,这样取数据才是先左再右。
图示:
代码:
//快速排序 - 非递归
void QuickSortNoR(int* a, int begin, int end)
{stack<int> st;//定义一个栈st.push(end);//先放右st.push(begin);//再放左while (!st.empty())//不为空进入循环{int left = st.top();//取左值st.pop();//删除栈顶元素int right = st.top();//取右值st.pop();//删除栈元素int ki = partsort3(a, left, right);//一趟排序确定某个元素的位置,返回该位置if (ki + 1 < right)//整体先放右{st.push(right);//里面先放右st.push(ki + 1);//里面再放左}if (left < ki - 1)//整体再放左{st.push(ki - 1);//里面先放右st.push(left);//里面再放左}}
}
快速排序特性总结:
- 时间复杂度:O(N * logN)
- 空间复杂度:O(logN)
- 不稳定
二、归并排序
2.1 递归
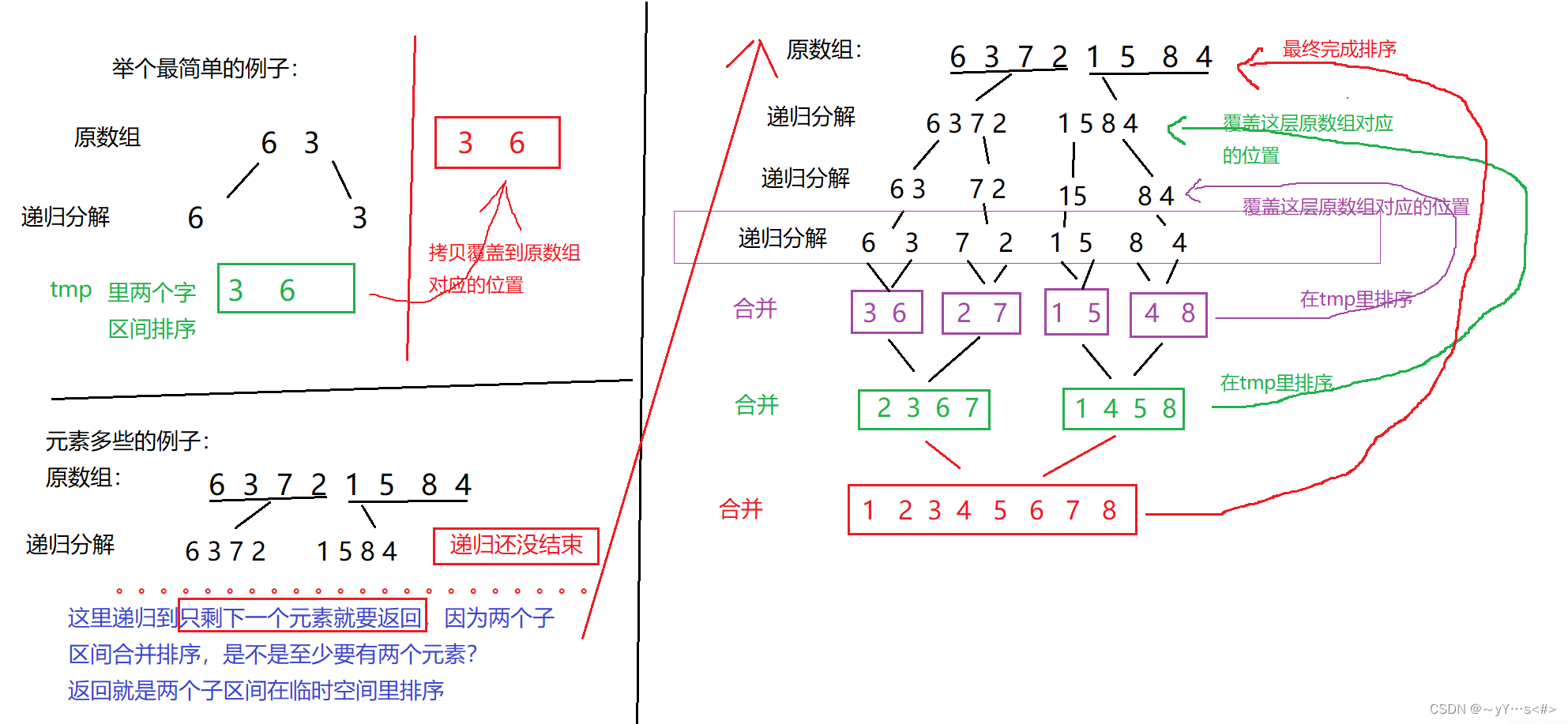
归并排序的递归采用二叉树的后序遍历的思想,先分解成小块区间,然后再合并两个小块空间的同时将这两块子区间的元素进行排序。依次类推。这里还要额外开辟一块临时空间,用来对两个子区间排序,在临时空间排完序后,然后把已经排序的元素的拷贝到原数组对应的位置,最终将整个数组排完序。
图示:
代码:
//归并排序-递归
void MergeSort(int* a, int* tmp, int begin, int end)
{//区间内元素个数小于等于1返回if (begin >= end){return;}int mid = (begin + end) / 2;//取划分区域的下标MergeSort(a, tmp, begin, mid);//递归左边MergeSort(a, tmp, mid + 1, end);//递归右边int begin1 = begin, end1 = mid;//合并的第一块小区间int begin2 = mid + 1, end2 = end;//合并的第二块小区间int k = begin;//注意k为begin当前区域的初始位置while (begin1 <= end1 && begin2 <= end2){ // 谁小谁先放入tmpif (a[begin1] <= a[begin2]){tmp[k++] = a[begin1++];}else{tmp[k++] = a[begin2++];}}// 哪块小区间有剩余,直接放入tmpwhile (begin1 <= end1){tmp[k++] = a[begin1++];}while (begin2 <= end2){tmp[k++] = a[begin2++];}//最后拷贝到原数组对应的位置,完成排序memcpy(a + begin, tmp + begin, sizeof(int) * (end2 - begin + 1));
}
2.2 非递归
归并排序的非递归也是模拟递归的过程,只是没有递,只有归,即只有合并的过程,用for循环控制合并区间的大小和范围即可,也要借助临时空间来排序,最后拷贝给原数组。
图示:
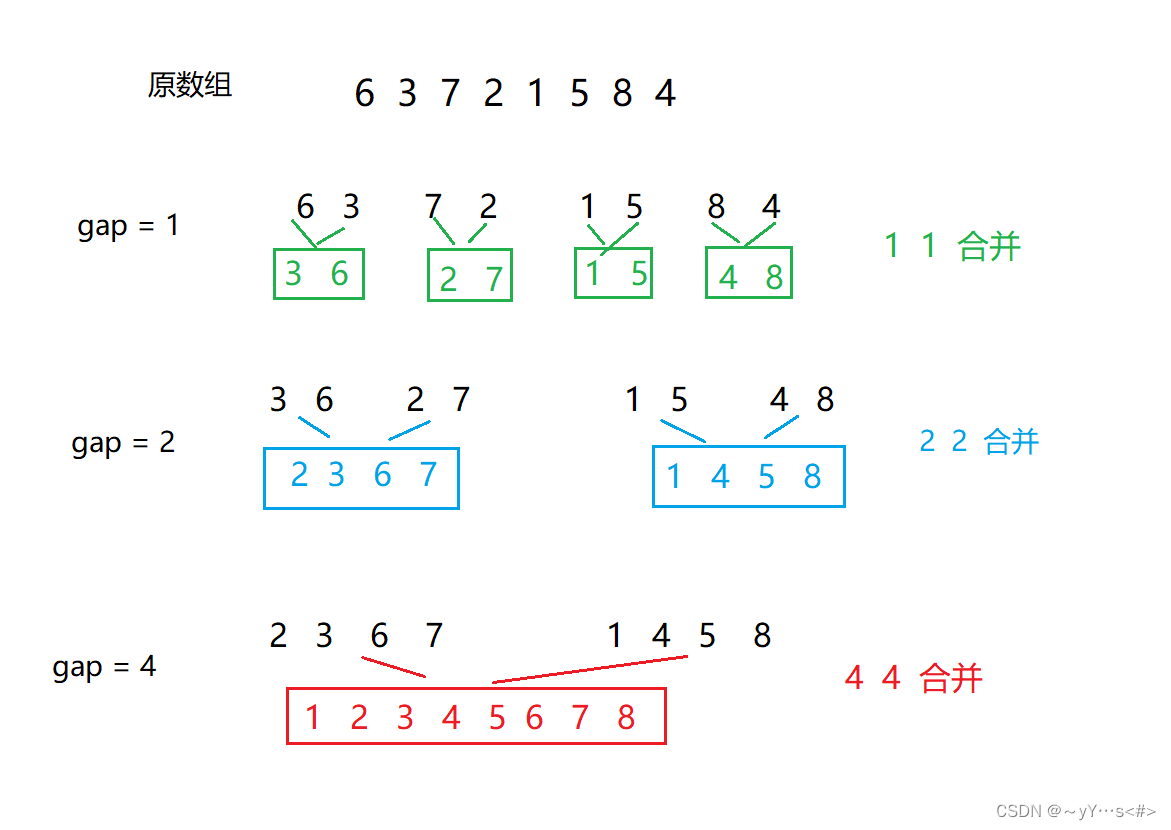
代码:
//归并排序-非递归
void MergeSortNoR(int* a, int* tmp, int n)
{int gap = 1;//初始合并的子区间大小while (gap < n)//范围{for (int i = 0; i < n; i += gap * 2){int begin1 = i, end1 = i + gap - 1;//合并的第一块小区间int begin2 = i + gap, end2 = i + gap * 2 - 1;//合并的第二块小区间int k = i;if (begin2 >= n)//只有第一块小区间,没有第二块小区间{break;//不能合并,跳出}if (end2 >= n)//第二块小区间个数较少,但是不影响合并{end2 = n - 1;//修改end2的值}while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){tmp[k++] = a[begin1++];}else{tmp[k++] = a[begin2++];}}while (begin1 <= end1){tmp[k++] = a[begin1++];}while (begin2 <= end2){tmp[k++] = a[begin2++];}memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));//排序+拷贝回原数组}gap *= 2;//区间增大}
}
注意:
上面的代码有两个特殊处理用于非2的次方个元素的数组,如果begin2大于等于n,说明要合并的两个子区间仅仅只有第一块小区间,没有第二块小区间,这时就不需要合并了(第一块小区间在之前已经合并为有序)。如果end2大于等于n,第二块小区间还是存在的,只是元素个数少些,这时就把end2的指向的位置该成第二块小区间内最后一个元素的位置即可。
归并排序特性总结:
- 归并排序要额外开辟一块空间用来处理排序的问题
- 时间复杂度:O(N * logN)
- 空间复杂度:O(N)
- 稳定
相关文章:

【排序篇3】快速排序、归并排序
目录 一、快速排序1.1 递归1.2 非递归 二、归并排序2.1 递归2.2 非递归 一、快速排序 1.1 递归 快速排序的递归采用二叉树的前序遍历的思路,单趟排序先确定好一个元素的位置,然后往后递归再确定其他子区域内的某个元素的位置,直到只有一个元…...

Python中的@property
在 Python 中,property 是一种装饰器,用于将一个方法转换成只读属性。通过使用 property 装饰器,你可以定义一个类的方法,使其在访问时可以像访问属性一样,而不是通过方法调用。 下面是一个简单的例子来说明 property …...
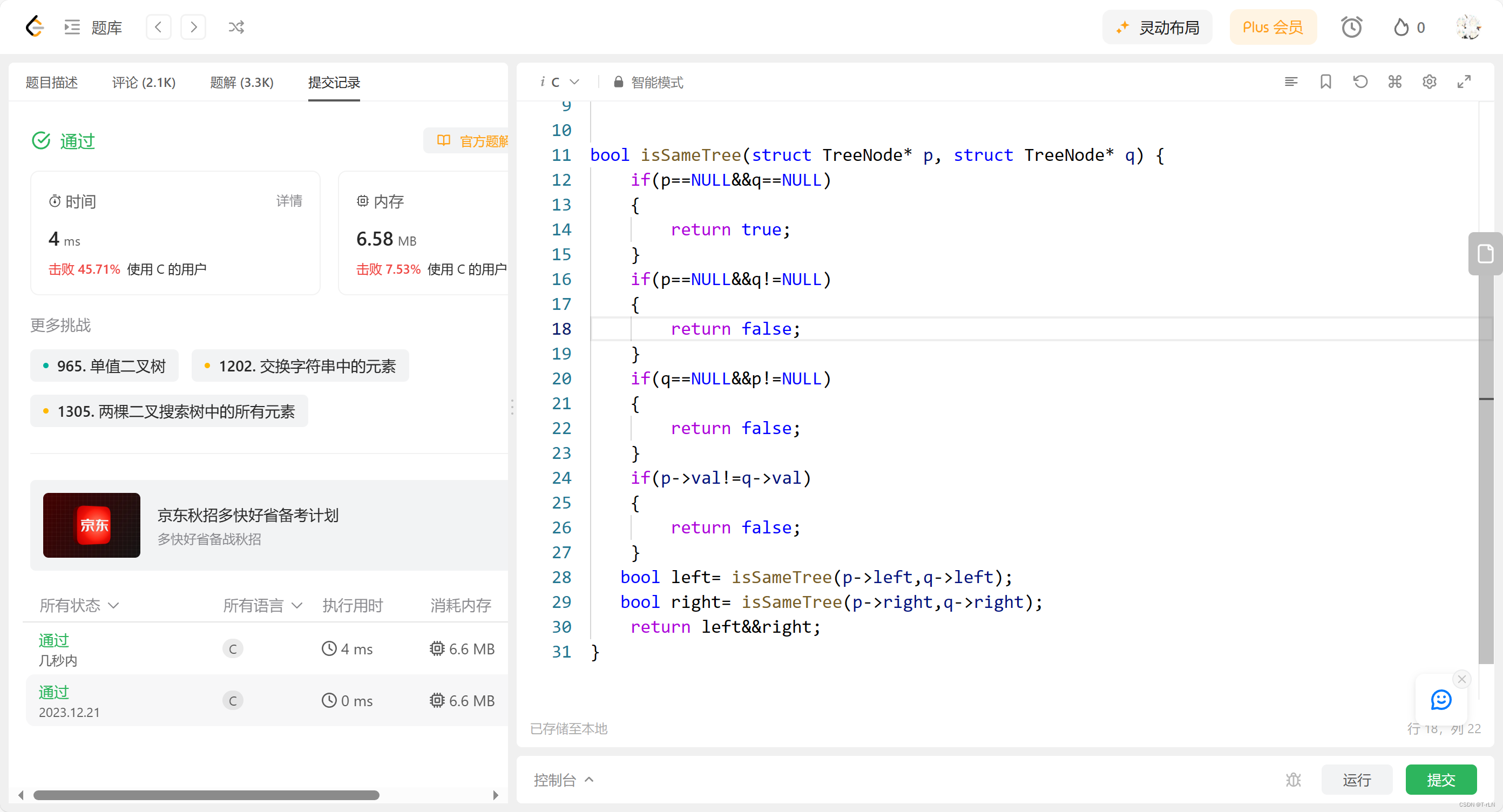
二叉树基础oj练习(单值二叉树、相同的树、二叉树的前序遍历)
讲了这么多数据结构相关的知识(可以看我的数据结构文章专栏): 抓紧刷题巩固一下了 目录 1.单值二叉树 题目描述 思路1 代码1 思路2 代码2 2.相同的树 题目描述 思路 代码 3.二叉树的前序遍历 代码 思路 1.单值二叉树 965. 单值二叉树 - 力扣(LeetCod…...
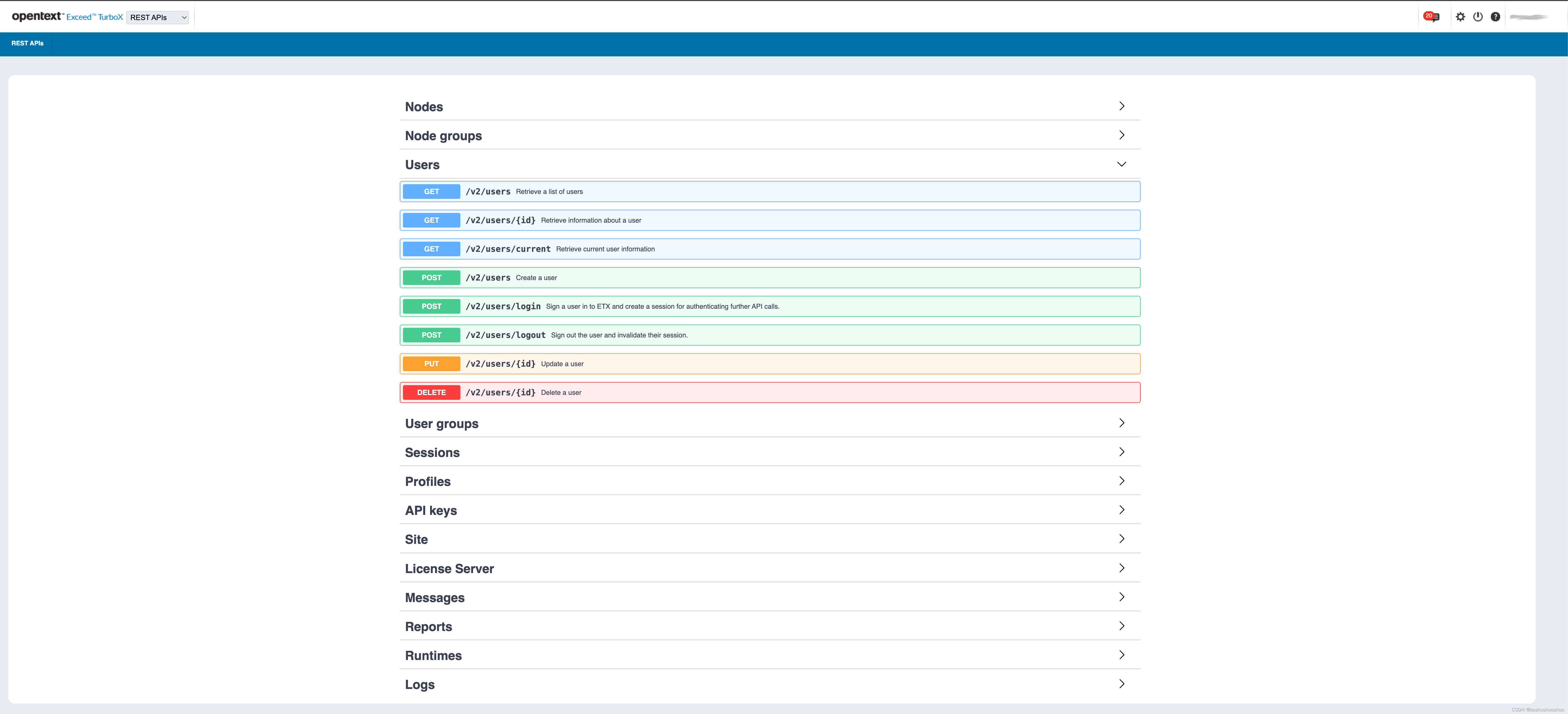
自动化创建ETX用户帐号
在芯片设计行业,ETX是常见的远程访问环境。用户在通过ETX访问远程环境前必须首先加入ETX系统,然后通过profile分配相关的环境的访问权限。 通常这些操作在ETX WEB页面手工操作,如果我们期望实现用户帐号注册全自动化,就需要将以上…...

Android 实现集合去重的方法
方法一:使用HashSet 将集合转换为HashSet。 Set<String> set new HashSet<>(list);将HashSet转换回List。 List<String> uniqueList new ArrayList<>(set);方法二:使用Java 8的Stream API 将列表转换为Stream。 Stream&l…...
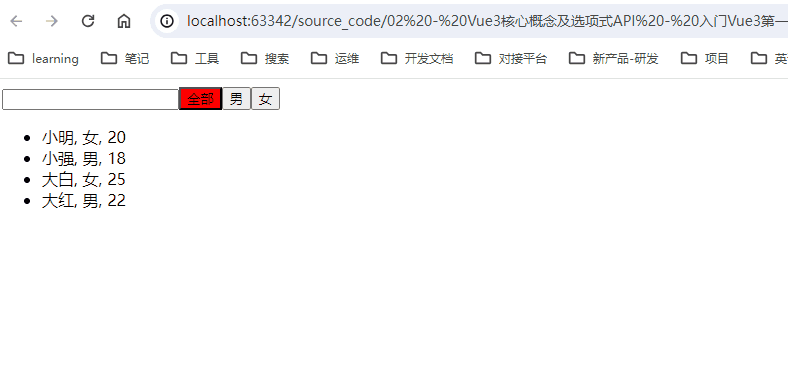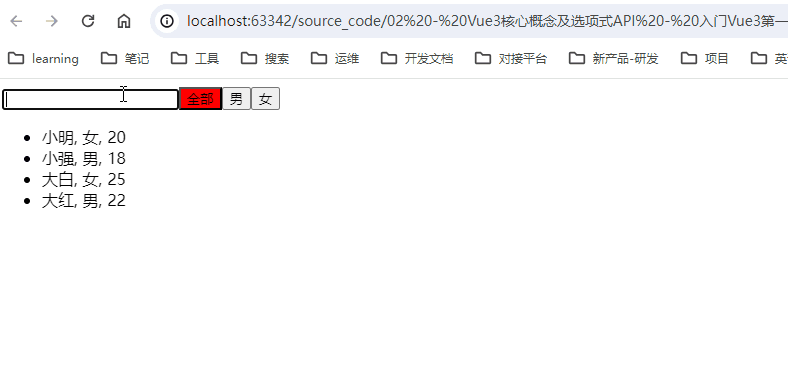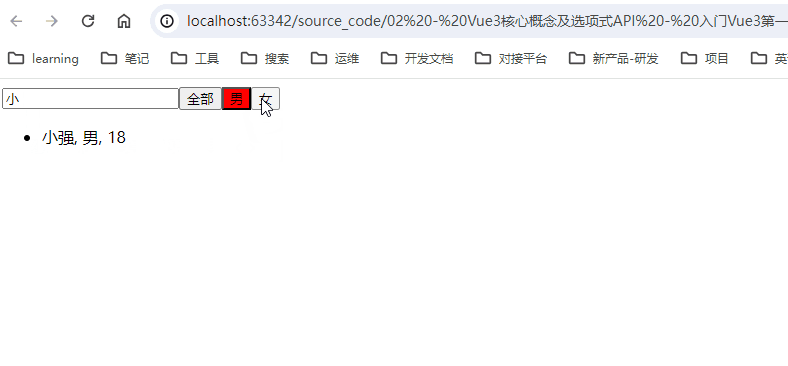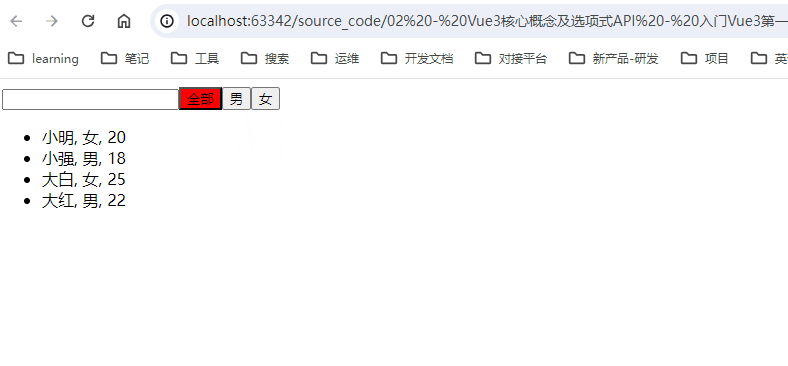
【Vue3】2-12 : 【案例】搜索关键词加筛选条件的综合
本书目录:点击进入 一、【案例】搜索关键词加筛选条件的综合 1.1、逻辑 1.2、效果 1.3、json数据 - 02-data.json 1.4、代码 一、【案例】搜索关键词加筛选条件的综合 1.1、逻辑 计算属性 - 绑定list,并过滤 input 双向绑定 - 当input改变时&…...
unity小程序websocket:nginx配置https (wss)转http (ws)及其他问题解决
目录 前言 实际运用场景 处理流程如下 nginx配置ssl和wss 配置过程中遇到的问题 1、无法连接服务器 2、通过IP可以访问,域名却不行 问题描述 解决 3、如何判断该域名是否备案了 前言 为了服务器网络的通用性,我们在实现移动端的游戏转微信小程序…...

MySql数据库对接Orcal数据库,需要考虑的前提问题
1.主表 从表的表关系;主键id 的关联问题; 2.字段类型的一致性问题(备注:像varchar类型的一点要谨防数据过长抛错); 3.实体类字段两表一致性问题; 4.入表不为空问题,判空尽量在实体…...

K8S的存储卷---数据卷
容器内的目录和宿主机的目录进行挂载 容器在系统上的生命周期是短暂的。delete,K8S用控制器创建的pod,delete相当于重启,容器的状态也会恢复到初始状态。一旦回到初始状态,所有的后天编辑的文件都会消失 容器和节点之间创建一个…...

【量化交易故事】小明开启了量化创业之旅-01
故事开始于2023年的春天,小明是一位对金融市场充满热情的IT工程师。在经历了数次基于主观判断和个人情绪进行投资却收获平平后,他意识到传统交易方式中的人为因素难以避免,而这往往成为影响投资决策稳定性和准确性的关键障碍。在一次偶然的机…...

ffmpeg写YUV420文件碰到阶梯型横线或者条纹状画面的原因和解决办法
版权声明:本文为CSDN博主「文三~」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。 原文链接:https://blog.csdn.net/asdasfdgdhh/article/details/112831581 看到了,转载,留着备份…...
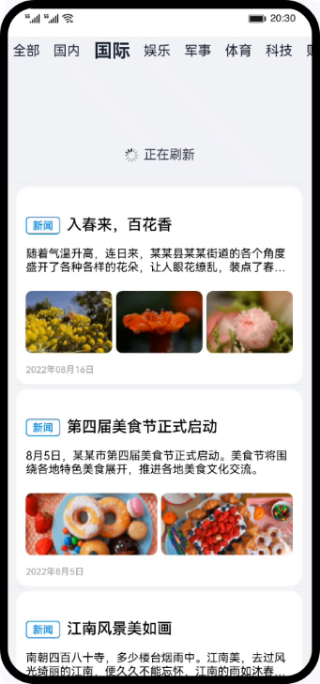
案例:新闻数据加载
文章目录 介绍相关概念相关权限约束与限制完整示例 代码结构解读构建主界面数据请求下拉刷新总结 介绍 本篇Codelab是基于ArkTS的声明式开发范式实现的样例,主要介绍了数据请求和touch事件的使用。包含以下功能: 数据请求。列表下拉刷新。列表上拉加载…...
数学的雨伞下:理解世界的乐趣
这本书没有一个公式,却讲透了数学的本质! 《数学的雨伞下:理解世界的乐趣》。一本足以刷新观念的好书,从超市到对数再到相对论,娓娓道来。对于思维空间也给出了一个更容易理解的角度。 作者:米卡埃尔•洛奈…...
)
补充 vue3用户管理权限(路由控制)
之前有人问我 ,如果是二级路由如何添加,这里我做一个补充吧。直接拿方法去用就行。也不做解释了。稍微看下就能看懂了 假设,后端返回给我们一个数据 [“/defa”,"/defa/defa1"] 这样的一个路由表,我们就需要通过这个路…...
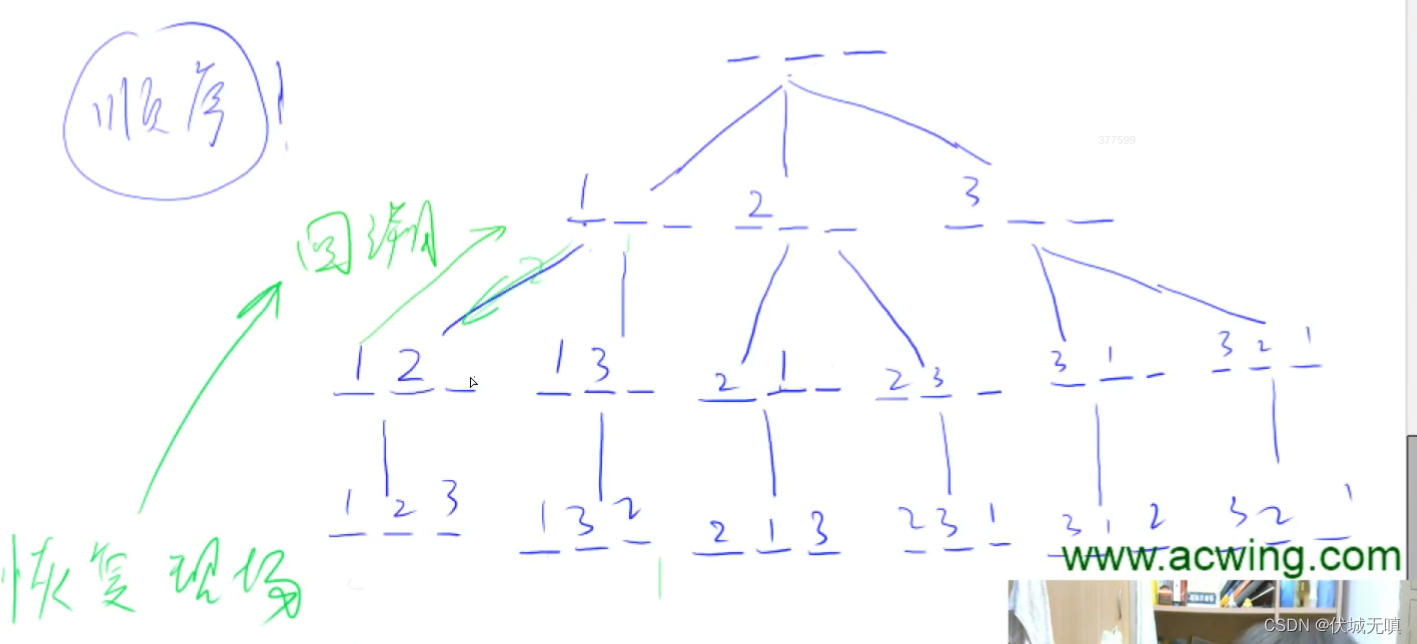
C++ 深度优先搜索DFS || 模版题:排列数字
给定一个整数 n ,将数字 1∼n 排成一排,将会有很多种排列方法。 现在,请你按照字典序将所有的排列方法输出。 输入格式 共一行,包含一个整数 n 。 输出格式 按字典序输出所有排列方案,每个方案占一行。 数据范围 1…...
计算机找不到msvcp120.dll如何解决?总结五个可靠的教程
在计算机使用过程中,遇到“找不到msvcp120.dll”这一问题常常令人困扰。msvcp120.dll作为Windows系统中至关重要的动态链接库文件,对于许多应用程序的正常运行起着不可或缺的作用。那么,究竟是什么原因导致找不到msvcp120.dll呢?又…...

法线变换矩阵的推导
背景 在冯氏光照模型中,其中的漫反射项需要我们对法向量和光线做点乘计算。 从顶点着色器中读入的法向量数据处于模型空间,我们需要将法向量转换到世界空间,然后在世界空间中让法向量和光线做运算。这里便有一个问题,如何将法线…...
React.Children.map 和 js 的 map 有什么区别?
JavaScript 中的 map 不会对为 null 或者 undefined 的数据进行处理,而 React.Children.map 中的 map 可以处理 React.Children 为 null 或者 undefined 的情况。 React 空节点:可以由null、undefined、false、true创建 import React from reactexport …...

13.Kubernetes部署Go应用完整流程:从Dockerfile到Ingress发布完整流程
本文以一个简单的Go应用Demo来演示Kubernetes应用部署的完整流程 1、Dockerfile多阶段构建 Dockerfile多阶段构建 [root@docker github]# git clone https://gitee.com/yxydde/http-dump.git [root@docker github]# cd http-dump/ [root@docker http-dump]# cat Dockerfile …...
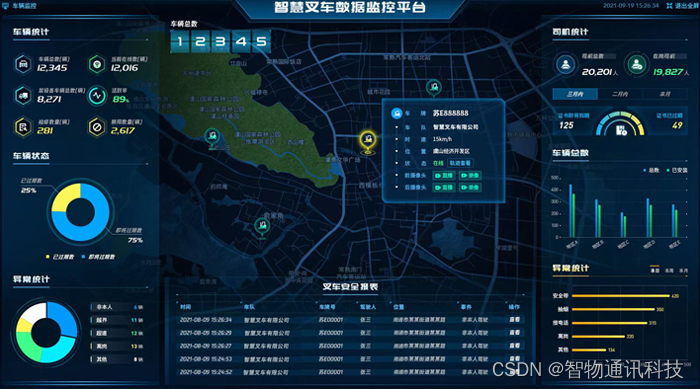
叉车车载终端定制_基于MT6762安卓核心板的车载终端设备方案
叉车车载终端是一款专为叉车车载场景设计的4英寸Android车载平板电脑。它采用了高能低耗的8核ARM架构处理器和交互开放的Android 12操作系统,算力表现强大。此外,该产品还具备丰富的Wi-Fi-5、4G LTE和蓝牙等通讯功能,可选配外部车载蘑菇天线&…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...
