求斐波那契数列矩阵乘法的方法
斐波那契数列
先来简单介绍一下斐波那契数列:
斐波那契数列是指这样一个数列:1,1,2,3,5,8,13,21,34,55,89……这个数列从第3项开始 ,每一项都等于前两项之和。
现在要求斐波那契数列的第n项,如果用Java代码层面来讲就是下面这样。
一个for循环,声明一个变量累加到第n项即可。 O ( N ) O(N) O(N)的时间复杂度。但这并不是最优解,最优解的时间复杂度是 O ( L o g N ) O(LogN) O(LogN)。
最优解怎么得到的?是根据上面斐波那契数列的递推式: F ( n ) = F ( n − 1 ) + F ( n − 2 ) F(n) = F(n - 1) + F(n - 2) F(n)=F(n−1)+F(n−2),
这是一项严格的递推式,在告诉初始值的情况下,如果后面的每一项都按照严格的递推式可以推出来,那都有 O ( L o g N ) O(LogN) O(LogN)的方法。
那什么没有 O ( L o g N ) O(LogN) O(LogN)的方法呢? 比如说有一个左数列。得到这个左数列的第n项。
给定的信息比如有一个 boolean[] b = {T , T , F , F , T , T , T}。 对于左数列来说,第一项是1,第二项也是1,之后的每一项根据是T还是F来进行表达。 如果当前项是 F ,则 F ( n ) = F ( n − 1 ) F(n) = F(n - 1) F(n)=F(n−1) ,如果当前项是 T,则 F ( n ) = F ( n − 1 ) + F ( n − 2 ) F(n) = F(n - 1) + F(n - 2) F(n)=F(n−1)+F(n−2)。以此来决定下一项值是什么。
所以根据公式:第三项 = 1,第四项 = 1,第五项 = 2 以此类推…。这种就没有 O ( L o g N ) O(LogN) O(LogN)的方法,因为会根据不同的条件进行条件转移。
斐波那契数列就是没有条件转移的严格递推式。这种都有 O ( L o g N ) O(LogN) O(LogN)的方法。
线性代数
如果 F ( n ) = F ( n − 1 ) + F ( n − 2 ) F(n) = F(n - 1) + F(n - 2) F(n)=F(n−1)+F(n−2),第n项和 F(n - 1) 和 F(n - 2)是严格关系,那在公式中,减的最多的常数是2,那就可以说它是一个二阶递推,依然是以斐波那契数列来举例。
已知斐波那契数列的第一项 F(1) = 1,第二项 F(2) = 1,那一定会存在下面这个关系:
∣ F 3 , F 2 ∣ = ∣ F 2 , F 1 ∣ × ∣ a b c d ∣ |F_3,F_2| = |F_2,F_1| \times\left| \begin{matrix} a & b \\ c & d \end{matrix} \right| ∣F3,F2∣=∣F2,F1∣× acbd
没有为什么,龟腚!
同样的,斐波那契数列的第四项F(4)和第三项F(3) 的行列式一定等于下面的式子(abcd为相同的2 * 2矩阵)。
∣ F 4 , F 3 ∣ = ∣ F 3 , F 2 ∣ × ∣ a b c d ∣ |F_4,F_3| = |F_3,F_2| \times\left| \begin{matrix} a & b \\ c & d \end{matrix} \right| ∣F4,F3∣=∣F3,F2∣× acbd
那这个2 * 2矩阵的abcd是什么呢? 接下来我们算一下
因为斐波那契数列的前几项我们都是已知的,所以可以先列出来:
F(1) = 1, F(2) = 1,F(3) = 2,F(4) = 3,接下来我们带入到式子中。
∣ F 3 , F 2 ∣ = ∣ F 2 , F 1 ∣ × ∣ a b c d ∣ − > ∣ 2 , 1 ∣ = ∣ 1 , 1 ∣ × ∣ a b c d ∣ |F_3,F_2| = |F_2,F_1| \times\left| \begin{matrix} a & b \\ c & d \end{matrix} \right| ->|2,1| = |1,1| \times\left| \begin{matrix} a & b \\ c & d \end{matrix} \right| ∣F3,F2∣=∣F2,F1∣× acbd −>∣2,1∣=∣1,1∣× acbd
矩阵乘法:
F 2 ∗ a + F 1 ∗ c = F 3 F_2 * a + F_1 * c = F_3 F2∗a+F1∗c=F3 , F 2 ∗ b + F 1 ∗ d = F 2 F_2 * b + F_1 * d = F_2 F2∗b+F1∗d=F2
带入进来就是 :
{ a + c = 2 b + d = 1 (1) \begin{cases} a + c = 2 \\ b + d = 1 \end{cases} \tag{1} {a+c=2b+d=1(1)
一个式子不够,求不出来,再次带入下一个公式:
∣ F 4 , F 3 ∣ = ∣ F 3 , F 2 ∣ × ∣ a b c d ∣ − > ∣ 3 , 2 ∣ = ∣ 2 , 1 ∣ × ∣ a b c d ∣ |F_4,F_3| = |F_3,F_2| \times\left| \begin{matrix} a & b \\ c & d \end{matrix} \right|->|3,2| = |2,1| \times\left| \begin{matrix} a & b \\ c & d \end{matrix} \right| ∣F4,F3∣=∣F3,F2∣× acbd −>∣3,2∣=∣2,1∣× acbd
矩阵乘法:
F 3 ∗ a + F 2 ∗ c = F 4 F_3 * a + F_2 * c = F_4 F3∗a+F2∗c=F4 , F 3 ∗ b + F 2 ∗ d = F 3 F_3 * b + F_2 * d = F_3 F3∗b+F2∗d=F3
带入进来就是 :
{ 2 a + c = 3 2 b + d = 2 (2) \begin{cases} 2a + c = 3 \\ 2b + d = 2 \end{cases} \tag{2} {2a+c=32b+d=2(2)
求出:a = 1 , b = 1, c = 1 ,d = 0
再次带入验证一下:
∣ F 5 , F 4 ∣ = ∣ F 4 , F 3 ∣ × ∣ a b c d ∣ − > ∣ F 5 , F 4 ∣ = ∣ 3 , 2 ∣ × ∣ 1 1 1 0 ∣ |F_5,F_4| = |F_4,F_3| \times\left| \begin{matrix} a & b \\ c & d \end{matrix} \right|->|F_5,F_4| = |3,2| \times\left| \begin{matrix} 1 & 1 \\ 1 & 0 \end{matrix} \right| ∣F5,F4∣=∣F4,F3∣× acbd −>∣F5,F4∣=∣3,2∣× 1110
矩阵乘法:
F 4 ∗ a + F 3 ∗ c = F 5 F_4 * a + F_3 * c = F_5 F4∗a+F3∗c=F5 , F 4 ∗ b + F 3 ∗ d = F 4 F_4 * b + F_3 * d = F_4 F4∗b+F3∗d=F4
3 + 2 = 5 3 + 2 =5 3+2=5 , 3 + 0 = 3 3 + 0 = 3 3+0=3
求出:F(5) = 5 , F(4) = 3。 证明我们求出的a,b,c,d是对的。
根据上面的公式可以列出:
{ ∣ F 3 , F 2 ∣ = ∣ F 2 , F 1 ∣ × ∣ 矩阵 ∣ ∣ F 4 , F 3 ∣ = ∣ F 3 , F 2 ∣ × ∣ 矩阵 ∣ ∣ F 5 , F 4 ∣ = ∣ F 4 , F 3 ∣ × ∣ 矩阵 ∣ . . . . . ∣ F n , F n − 1 ∣ = ∣ F n − 1 , F n − 2 ∣ × ∣ 矩阵 ∣ \begin{cases} |F_3,F_2| = |F_2,F_1| \times |矩阵|\\ |F_4,F_3| = |F_3,F_2| \times|矩阵|\\ |F_5,F_4| = |F_4,F_3| \times |矩阵|\\ .....\\ |F_n,F_{n-1}| = |F_{n-1},F_{n-2}| \times|矩阵| \end{cases} ⎩ ⎨ ⎧∣F3,F2∣=∣F2,F1∣×∣矩阵∣∣F4,F3∣=∣F3,F2∣×∣矩阵∣∣F5,F4∣=∣F4,F3∣×∣矩阵∣.....∣Fn,Fn−1∣=∣Fn−1,Fn−2∣×∣矩阵∣
推导一下,将相同的值带入可得出:
∣ F n , F n − 1 ∣ = ∣ F 2 , F 1 ∣ × ∣ 相同矩阵 ∣ n − 2 |F_n,F_{n-1}| = |F_2,F_1| \times\left| \begin{matrix} 相同矩阵 \end{matrix} \right|^{n-2} ∣Fn,Fn−1∣=∣F2,F1∣× 相同矩阵 n−2
再次回到求斐波那契数列第n项的问题。
我们目前已经推导出了最后的公式,那想要求斐波那契数列第n项的关键点是不是在于求矩阵的n - 2次方,只要矩阵的某次方算的足够快,第n项是不是求的就足够快!!!!
如何让一个数的次方算的足够快
在求得矩阵某次方之前,我们先来看看如何让一个普通的数,比如说 1 0 75 10^{75} 1075这个数算的足够快?
先来搞定这个数,相同的逻辑用在矩阵上,那同样矩阵也会非常快!
利用二进制!
1 0 75 10^{75} 1075如果是75个10相乘,那这是一个 O ( N ) O(N) O(N)的问题,不够快。
首先,将幂数75拆分成对应的二进制为01001011(64 + 8 + 2 + 1 ),再让变量 t = 1 0 1 10^1 101,t不断的和自己相乘变成 1 0 2 10^2 102、 1 0 4 10^4 104、 1 0 8 10^8 108… t 不断的追赶75不断的和自己相乘,那追赶75的一共追赶多少次? O ( L o g N ) O(LogN) O(LogN)次。
接下来将 变量t 和75的二进制进行融合。
t 没和自己相乘之前,是 1 0 1 10^1 101,我们总的结果 result,一开始是1,这时候看01001011,二进制中1的位置是有值的,说明这个值是我结果需要的,那就用 result * t ( 1 0 1 10^1 101)
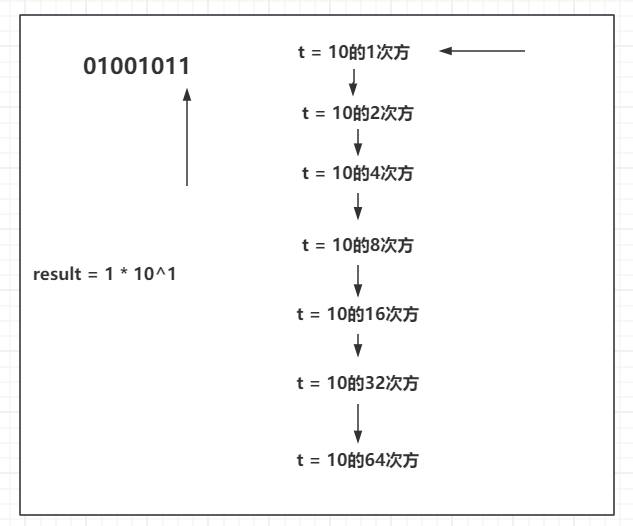
再接着往下来,01001011中2的位置也是1,代表这个位置也是结果需要的,将此时的 t 也乘进来。
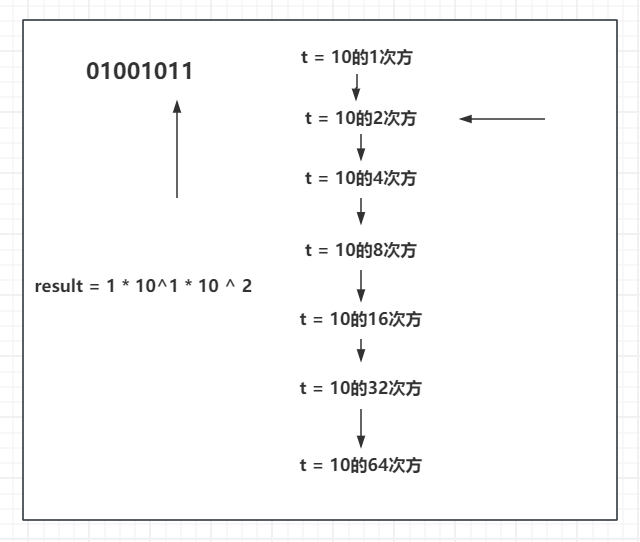
继续往下,此时来到了01001011中的4,4的二进制为0,代表结果不被需要,不需要就不乘这个数,t继续和自己相乘。
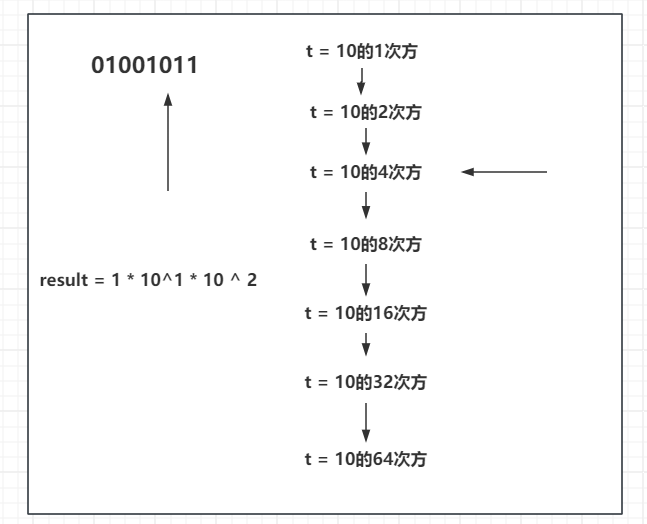
继续向下来到了01001011中的8。同样也是被需要的,将 1 0 8 10^8 108加到结果中。
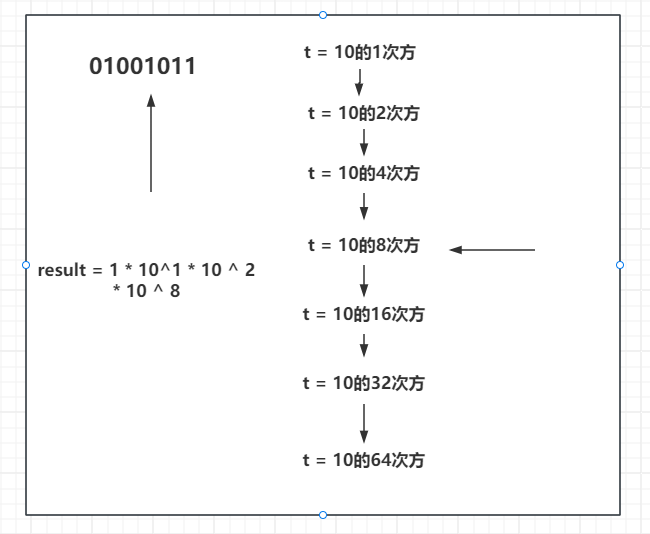
依次类推,继续向下,16 32 对应的2进制位置都为0,都不需要这两个数,直到来到了 1 0 64 10^{64} 1064次方,将需要的数都乘到结果中,就是最终答案。
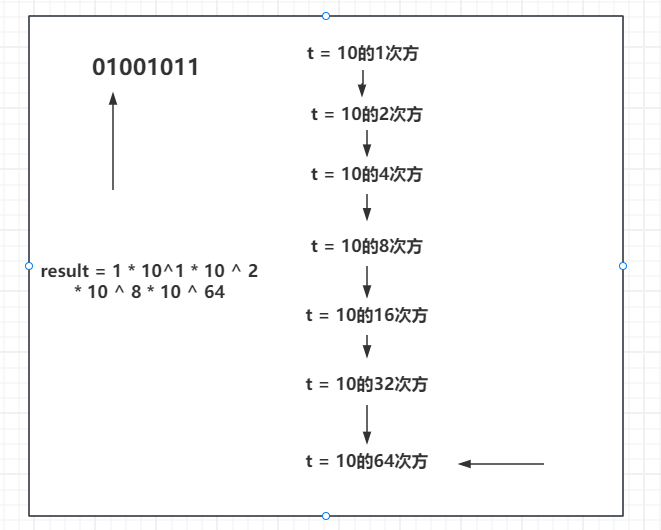
t 在不断和自己相乘的过程中,按位判断,要不要添加到结果中去。
为什么这么做?
其实追根究底是一个二分的过程,只不过自己二分的过程没有二进制提供的优良。
求一个数字的n次方我们已经解决了 ,那矩阵呢? 同理!
求一个矩阵的75次方
将矩阵的幂数进行二进制拆分,那在求 1 0 75 10^{75} 1075时,先搞了result = 1,如果这个数被需要,就乘到结果中,那换到矩阵中,是不是只要将result 的 1 变成矩阵中代表 1 的数就行了。t 同样也是变成 矩阵的 1次方, 矩阵的2次方,不断和自己相乘。
单位矩阵
单位矩阵中对角线上都是1剩下位置都是0就代表着1 。
∣ 1 0 0 0 1 0 0 0 1 ∣ \left| \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix} \right| 100010001
矩阵乘法
-
当矩阵A的列数等于矩阵B的行数时,A与B可以相乘。
-
矩阵C的行数等于矩阵A的行数,C的列数等于B的列数。
-
乘积C的第m行第n列的元素等于矩阵A的第m行的元素与矩阵B的第n列对应元素乘积之和
所以:A是一个 m × n 的矩阵,B是一个 n × p 的矩阵,C是一个 m × p 的矩阵。
∣ 1 2 3 4 ∣ ∗ ∣ 5 6 7 8 ∣ = ∣ 1 ∗ 5 + 2 ∗ 7 1 ∗ 6 + 2 ∗ 8 3 ∗ 5 + 4 ∗ 7 3 ∗ 6 + 4 ∗ 8 ∣ \left| \begin{matrix} 1 & 2 \\ 3 & 4 \\ \end{matrix} \right| * \left| \begin{matrix} 5 & 6 \\ 7 & 8 \end{matrix} \right|= \left| \begin{matrix} 1 * 5 + 2 * 7 & 1 * 6 + 2* 8 \\ 3 * 5 + 4 * 7 & 3 * 6 + 4 * 8 \end{matrix} \right| 1324 ∗ 5768 = 1∗5+2∗73∗5+4∗71∗6+2∗83∗6+4∗8
代码
因为是两个矩阵相乘,2 * 2的矩阵相得到的也一定是个2 * 2的矩阵,要求的是第F(n)项,根据上面的公式可以得出
F n = F 1 ∗ a + F 2 ∗ c Fn = F_1 * a + F_ 2 * c Fn=F1∗a+F2∗c 。 F(1) = 1 F2 = (1) ,所以我们最终结果只需要 res[0][0] + res[1][0] 即可。
public static int f2(int n){if (n == 0){return 0;}if (n == 1 || n == 2){return 1;}//斐波那契数列的单位矩阵int[][] base = {{1,1},{1,0}};int[][] res = matrixPower(base,n - 2);return res[0][0] + res[1][0];}public static int[][] matrixPower(int[][] m, int p) {int[][] res = new int[m.length][m[0].length];for (int i = 0; i < res.length; i++) {res[i][i] = 1;}// res = 矩阵中的1int[][] t = m;// 矩阵1次方for (; p != 0; p >>= 1) {if ((p & 1) != 0) {res = product(res, t);}t = product(t, t);}return res;}// 两个矩阵乘完之后的结果返回public static int[][] product(int[][] a, int[][] b) {int n = a.length;int m = b[0].length;int k = a[0].length; // a的列数同时也是b的行数int[][] ans = new int[n][m];for(int i = 0 ; i < n; i++) {for(int j = 0 ; j < m;j++) {for(int c = 0; c < k; c++) {ans[i][j] += a[i][c] * b[c][j];}}}return ans;}
相关文章:

求斐波那契数列矩阵乘法的方法
斐波那契数列 先来简单介绍一下斐波那契数列: 斐波那契数列是指这样一个数列:1,1,2,3,5,8,13,21,34,55,89……这个数列从第3项开始 &…...
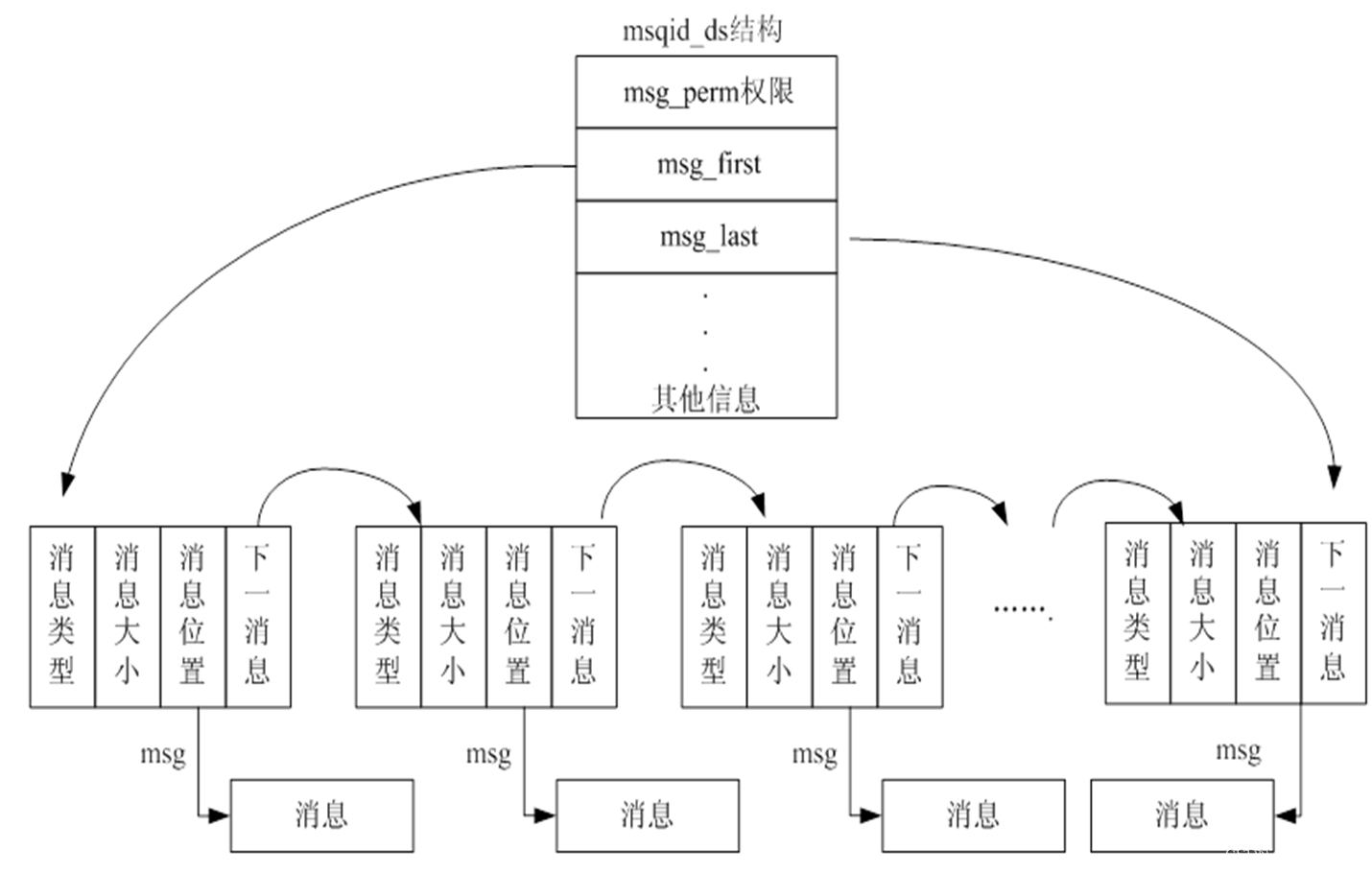
【IPC通信--消息队列】
消息队列(也叫做报文队列)是一个消息的链表。可以把消息看作一个记录,具有特定的格式以及特定的优先级。对消息队列有写权限的进程可以向消息队列中按照一定的规则添加新消息;对消息队列有读权限的进程则可以从消息队列中读走消息…...
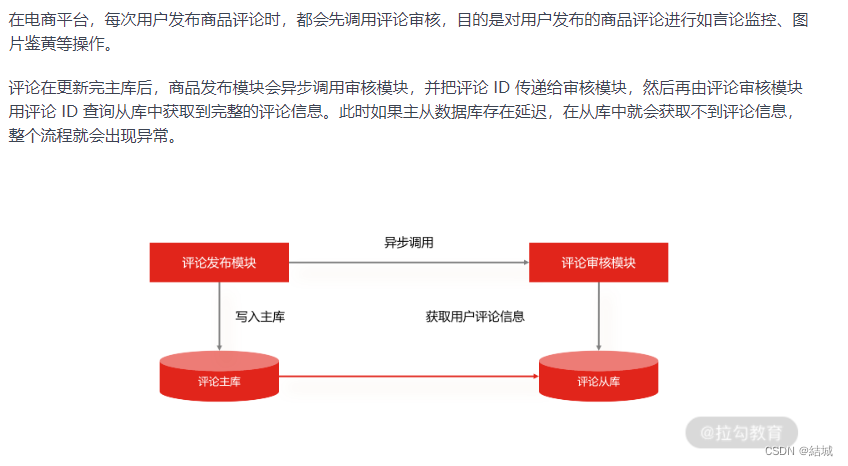
读写分离的手段——主从复制,解决读流量大大高于写流量的问题
应用场景 假设说有这么一种业务场景,读流量显著高于写流量,你要怎么优化呢。因为写是要加锁的,可能就会阻塞你读请求。而且其实读多写少的场景还很多见,比如电商平台,用户浏览n多个商品才会买一个。 大部分人的思路可…...
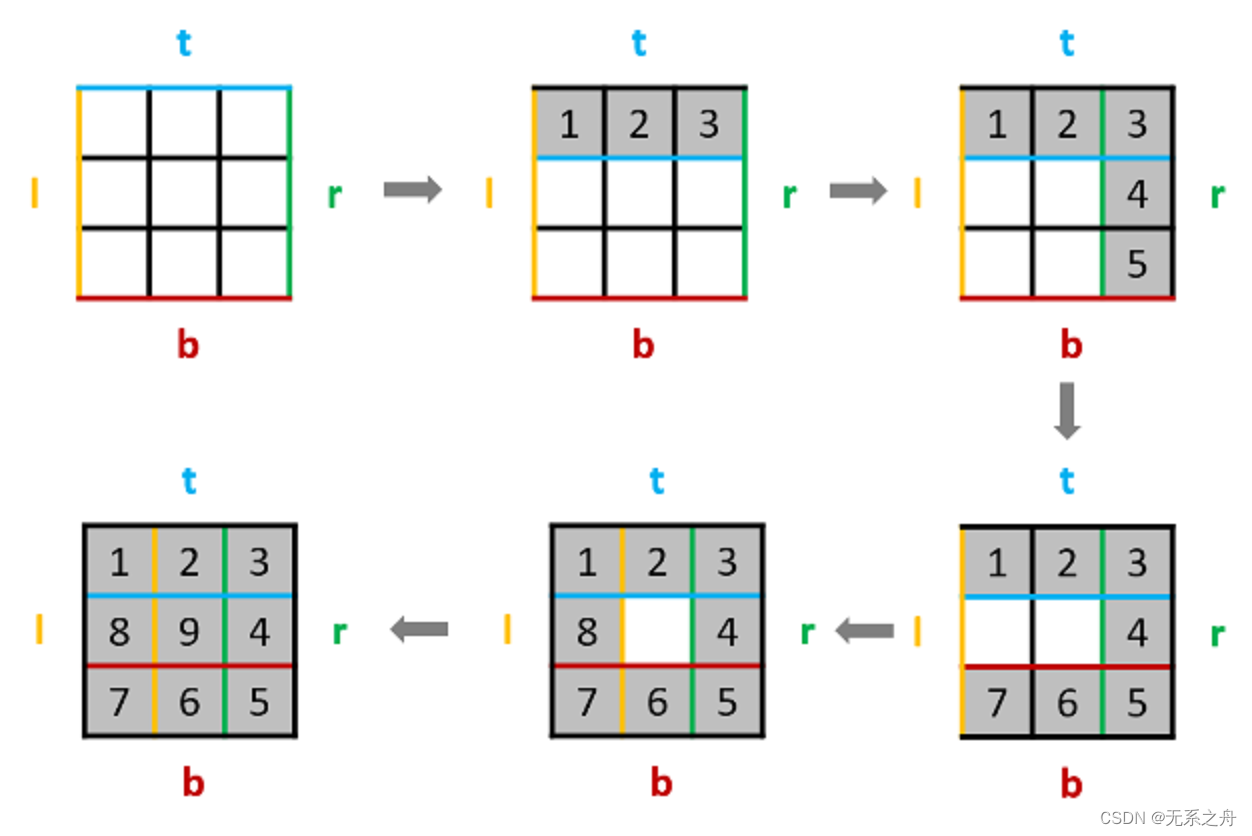
Day02
今日任务: 977 有序数组的平方209 长度最小的子数组59 螺旋矩阵Ⅱ 977 有序数组的平方 题目链接:https://leetcode.cn/problems/squares-of-a-sorted-array/ 双指针问题,以及数组本身时有序的; 思路: 左、右两个…...

编程语言的发展未来?
编程语言的未来? 随着科技的飞速发展,编程语言在计算机领域中扮演着至关重要的角色。它们是软件开发的核心,为程序员提供了与机器沟通的桥梁。那么,在技术不断进步的未来,编程语言的走向又将如何呢? 方向…...

docsify阿里云上部署
使用Markdown格式安装和部署Nginx 本文将介绍如何使用Markdown格式安装和部署Nginx。 步骤 安装Nginx: 打开终端,并根据您的操作系统执行以下命令来安装Nginx: 对于Ubuntu或Debian系统: sudo apt-get update sudo apt-get insta…...

GPT实战系列-简单聊聊LangChain搭建本地知识库准备
GPT实战系列-简单聊聊LangChain搭建本地知识库准备 LangChain 是一个开发由语言模型驱动的应用程序的框架,除了和应用程序通过 API 调用, 还会: 数据感知 : 将语言模型连接到其他数据源 具有代理性质 : 允许语言模型与其环境交互 LLM大模型…...
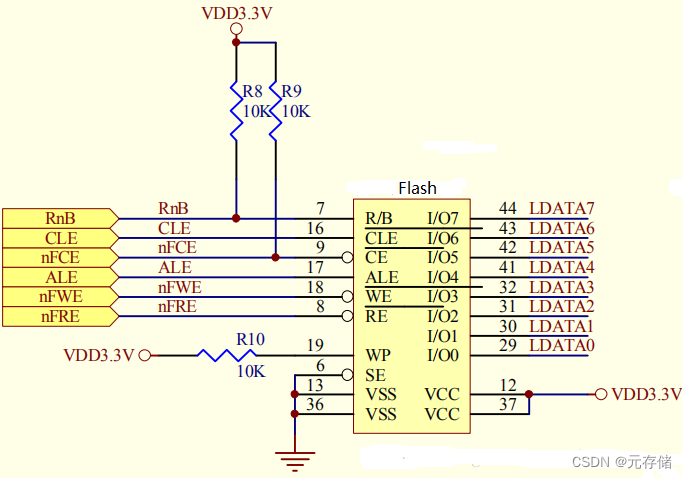
[NAND Flash 6.4] NAND FLASH基本读操作及原理_NAND FLASH Read Operation源码实现
依公知及经验整理,原创保护,禁止转载。 专栏 《深入理解NAND Flash》 <<<< 返回总目录 <<<< 全文 6000 字 内容摘要 NAND Flash 引脚功能 读操作步骤 NAND Flash中的特殊硬件结构 NAND Flash 读写时的数据流向 Read 操作时序 读时序操作过…...

opencv多张图片实现全景拼接
最近camera项目需要用到全景拼接,故此查阅大量资料,终于将此功能应用在实际项目上,下面总结一下此过程中遇到的一些问题及解决方式,同时也会将源码附在结尾处,供大家参考,本文采用的opencv版本为3.4.12。 首…...

深入理解UML中的继承关系
深入理解UML中的继承关系 在面向对象的设计中,继承关系是构建清晰、可维护系统的关键。统一建模语言(UML)提供了一种标准化的方法来可视化这些关系。本文将深入探讨UML中的继承关系,并探讨它如何在代码中体现。 什么是继承关系&a…...
CMU15-445-Spring-2023-Project #2 - B+Tree
前置知识:参考上一篇博文 CMU15-445-Spring-2023-Project #2 - 前置知识(lec07-010) CHECKPOINT #1 Task #1 - BTree Pages 实现三个page class来存储B树的数据。 BTree Page internal page和leaf page继承的基类,只包含两个…...
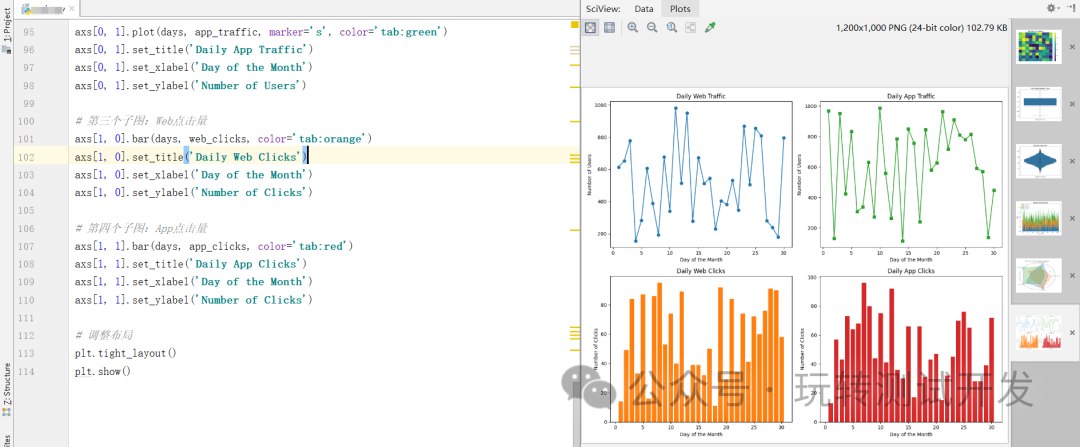
matplotlib:热图、箱形图、小提琴图、堆叠面积图、雷达图、子图
简介:在数字化的世界里,从Web、HTTP到App,数据无处不在。但如何将这些复杂的数据转化为直观、易懂的信息?本文将介绍六种数据可视化方法,帮助你更好地理解和呈现数据。 热图 (Heatmap):热图能有效展示用户…...
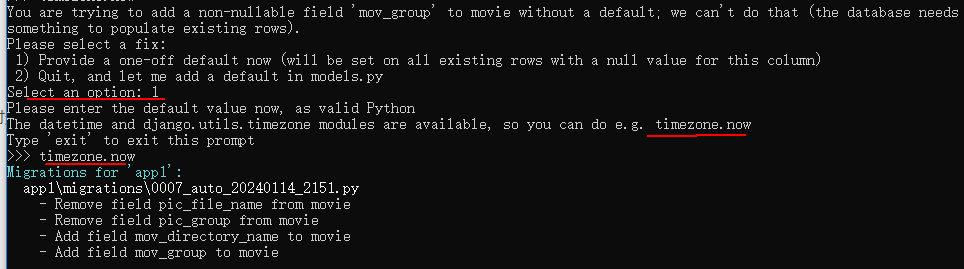
Django数据库选移的preserve_default=False是什么意思?
有下面的迁移命令: migrations.AddField(model_namemovie,namemov_group,fieldmodels.CharField(defaultdjango.utils.timezone.now, max_length30),preserve_defaultFalse,),迁移命令中的preserve_defaultFalse是什么意思呢? 答:如果模型定…...
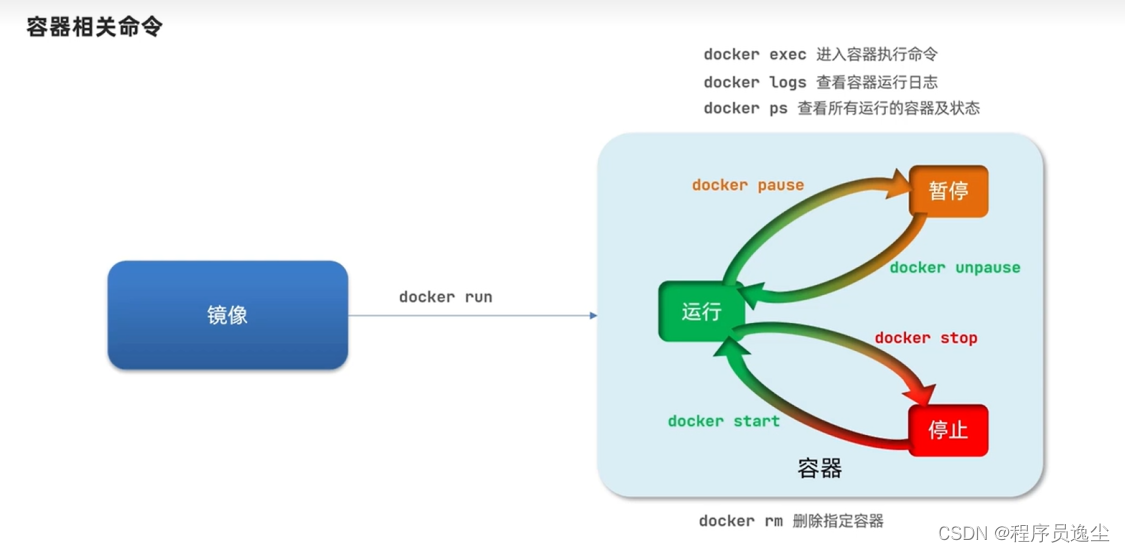
逸学Docker【java工程师基础】2.Docker镜像容器基本操作+安装MySQL镜像运行
基础的镜像操作 在这里我们的应用程序比如redis需要构建成镜像,它作为一个Docker文件就可以进行构建,构建完以后他是在本地的,我们可以推送到镜像服务器,逆向可以拉取到上传的镜像,或者说我们可以保存为压缩包进行相互…...
基于Java SSM框架实现医院管理系统项目【项目源码】计算机毕业设计
基于java的SSM框架实现医院管理系统演示 SSM框架 当今流行的“SSM组合框架”是Spring SpringMVC MyBatis的缩写,受到很多的追捧,“组合SSM框架”是强强联手、各司其职、协调互补的团队精神。web项目的框架,通常更简单的数据源。Spring属于…...
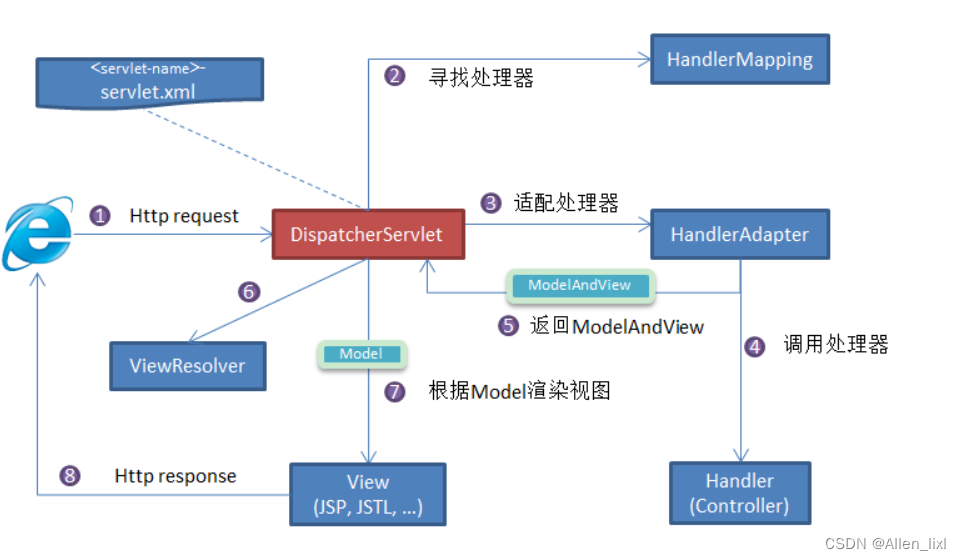
【java八股文】之Spring系列篇
【java八股文】之JVM基础篇-CSDN博客 【java八股文】之MYSQL基础篇-CSDN博客 【java八股文】之Redis基础篇-CSDN博客 【java八股文】之Spring系列篇-CSDN博客 【java八股文】之分布式系列篇-CSDN博客 【java八股文】之多线程篇-CSDN博客 【java八股文】之JVM基础篇-CSDN博…...

关于MySQL源码的学习 这里是一些建议
学习MySQL源码需要一定的编程基础,特别是C语言和数据结构。以下是一些建议,帮助你更好地入手学习MySQL源码: 基础知识 熟悉C语言编程基本概念、数据结构和算法。了解Linux操作系统基本概念,如进程、线程、内存管理、文件系统等。…...
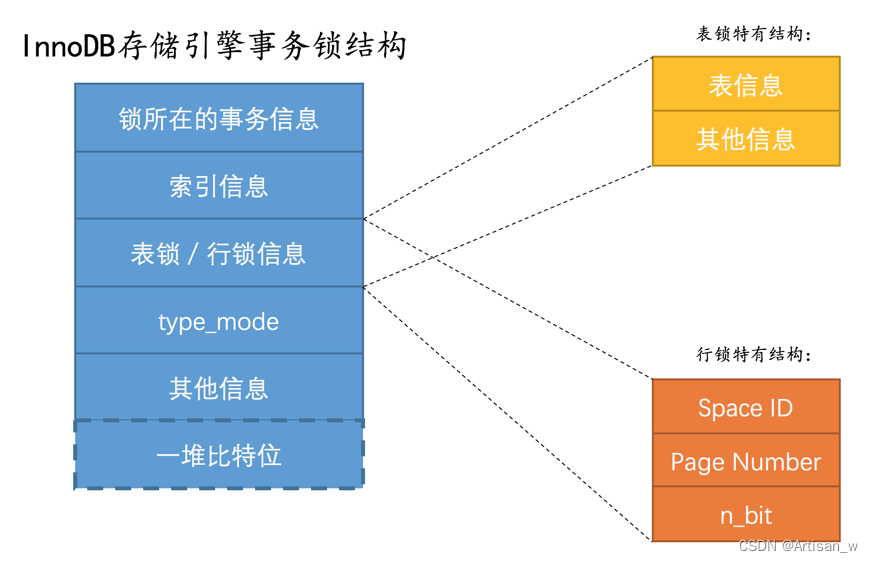
Mysql是怎样运行的--下
文章目录 Mysql是怎样运行的--下查询优化explainoptimizer_trace InnoDB的Buffer Pool(缓冲池)Buffer Pool的存储结构空闲页存储--free链表脏页(修改后的数据)存储--flush链表 使用Buffer PoolLRU链表的管理 事务ACID事务的状态事…...

yum来安装php727
yum 安装php727,一键安装,都是安装在系统的默认位置,方便快捷 先确定linux平台中centos的版本信息,一下内容针对el7 查看linux版本 : cat /etc/redhat-release 查看内核版本命令: cat /proc/version (0)如果有安装好…...

基于jackson封装的json字符串与javaBean对象转换工具
文章目录 一、概述二、编码实现1. pom文件引入组件2. 核心代码 三、功能测试1. 测试文件2. 测试代码 四,完整代码 一、概述 带有API接口交互的web项目开发过程中,json字符串与javaBean对象之间的相互转换是比较常见的需求,基于jackson Objec…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...

渗透实战PortSwigger Labs指南:自定义标签XSS和SVG XSS利用
阻止除自定义标签之外的所有标签 先输入一些标签测试,说是全部标签都被禁了 除了自定义的 自定义<my-tag onmouseoveralert(xss)> <my-tag idx onfocusalert(document.cookie) tabindex1> onfocus 当元素获得焦点时(如通过点击或键盘导航&…...

MLP实战二:MLP 实现图像数字多分类
任务 实战(二):MLP 实现图像多分类 基于 mnist 数据集,建立 mlp 模型,实现 0-9 数字的十分类 task: 1、实现 mnist 数据载入,可视化图形数字; 2、完成数据预处理:图像数据维度转换与…...
