机器学习~从入门到精通(二)线性回归算法和多元线性回归
为什么要做数据归一化
一、数据归一化:
1.最值归一化
2.均值方差归一化
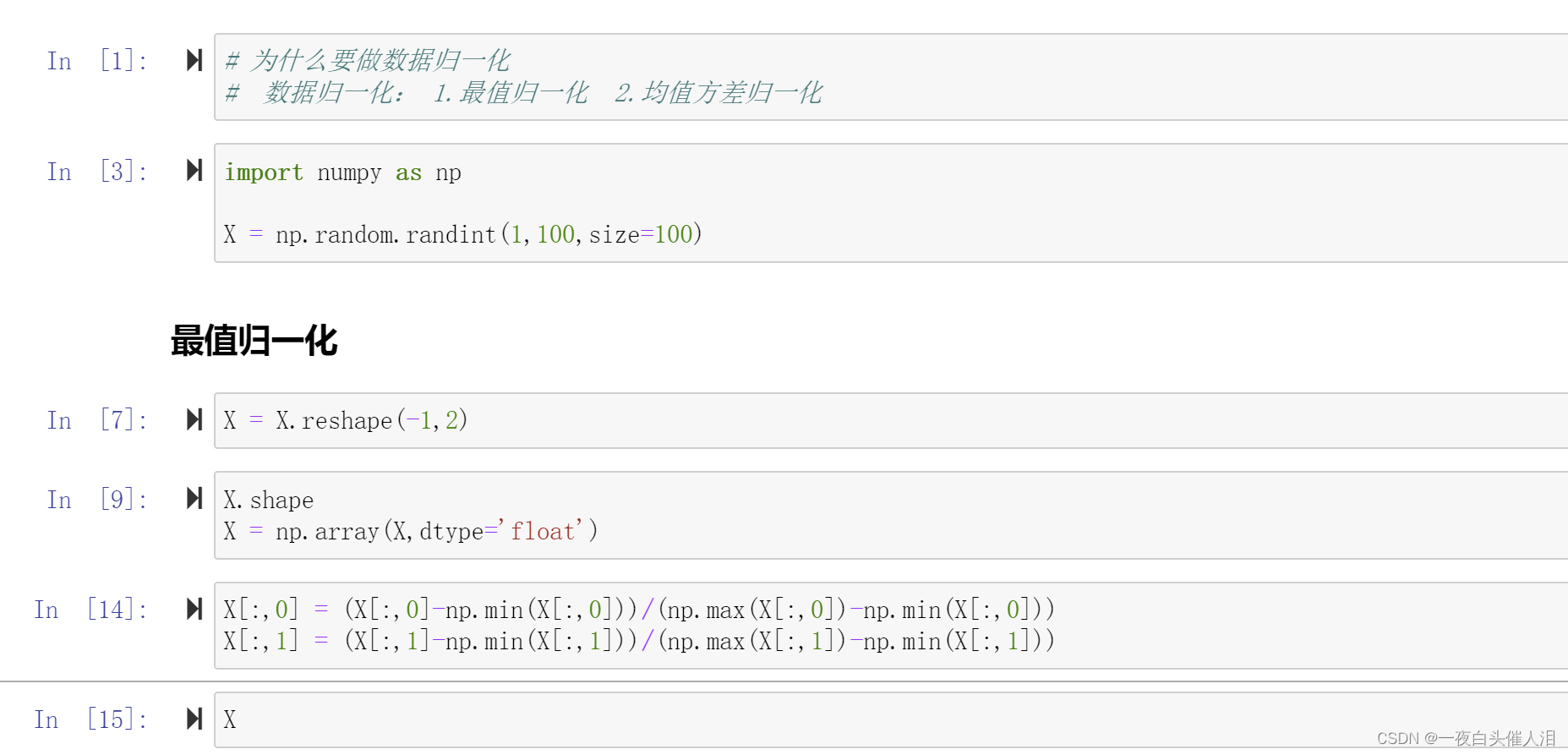
import numpy as npX = np.random.randint(1,100,size=100)
X = X.reshape(-1,2)
X.shape
X = np.array(X,dtype='float')
X[:,0] = (X[:,0]-np.min(X[:,0]))/(np.max(X[:,0])-np.min(X[:,0]))
X[:,1] = (X[:,1]-np.min(X[:,1]))/(np.max(X[:,1])-np.min(X[:,1]))
X
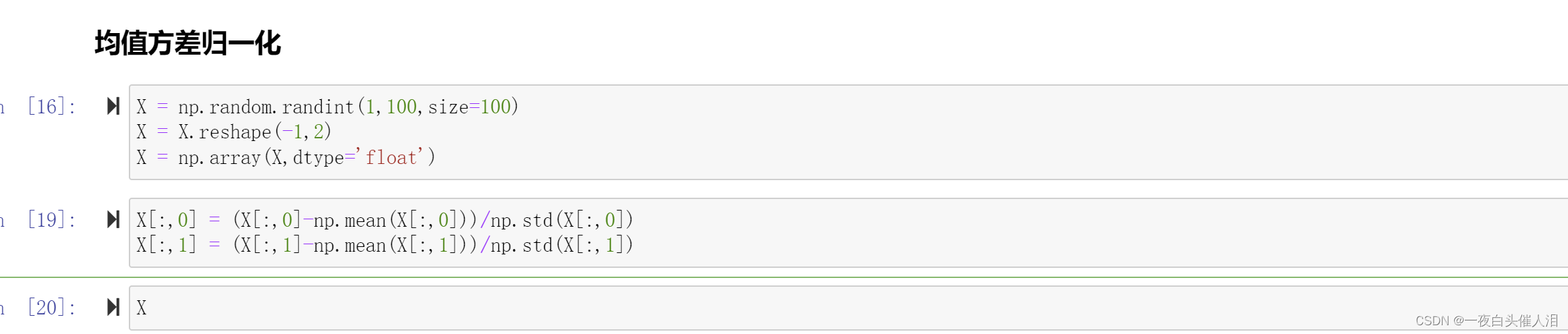
均值方差归一化
X = np.random.randint(1,100,size=100)
X = X.reshape(-1,2)
X = np.array(X,dtype='float')
X[:,0] = (X[:,0]-np.mean(X[:,0]))/np.std(X[:,0])
X[:,1] = (X[:,1]-np.mean(X[:,1]))/np.std(X[:,1])
X
np.std(X[:,0])
np.std(X[:,1])
np.mean(X[:,0])
np.mean(X[:,1])
二、数据归一化的注意事项
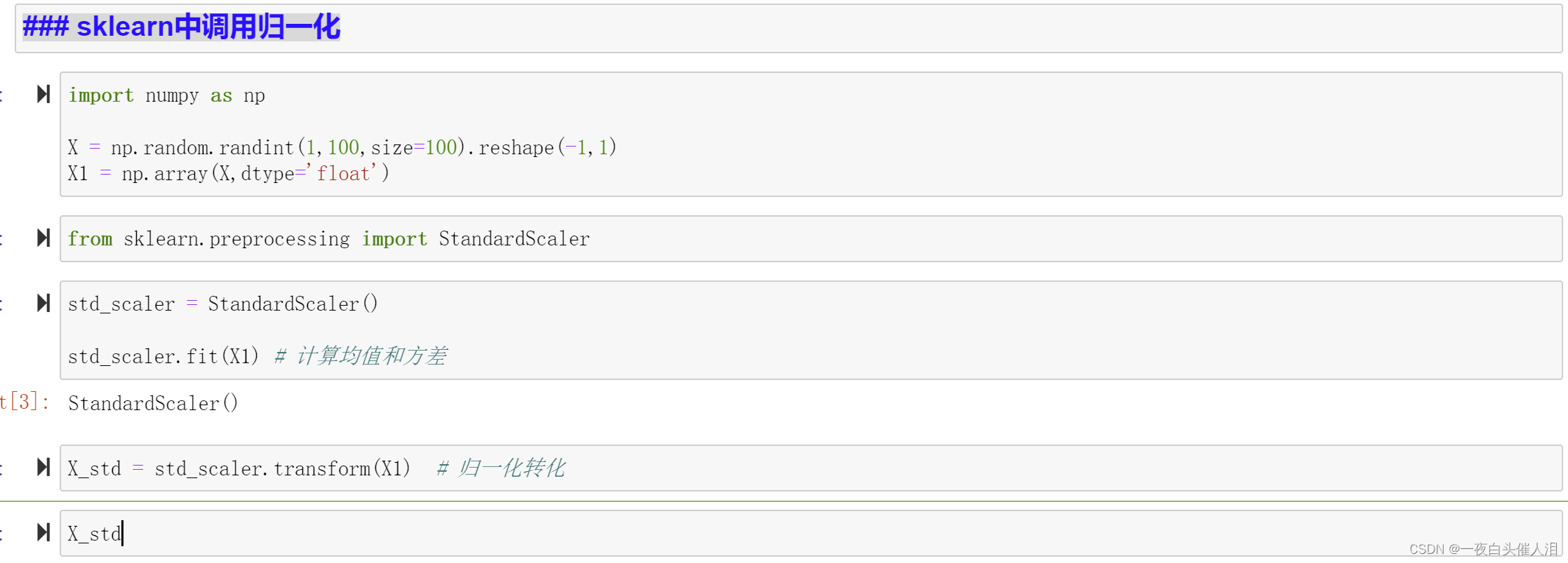
import numpy as npX = np.random.randint(1,100,size=100).reshape(-1,1)
X1 = np.array(X,dtype='float')from sklearn.preprocessing import StandardScaler
std_scaler = StandardScaler()std_scaler.fit(X1) # 计算均值和方差
X_std = std_scaler.transform(X1) # 归一化转化
X_std
三、鸢尾花数据归一化
import numpy as np
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaleriris = load_iris()
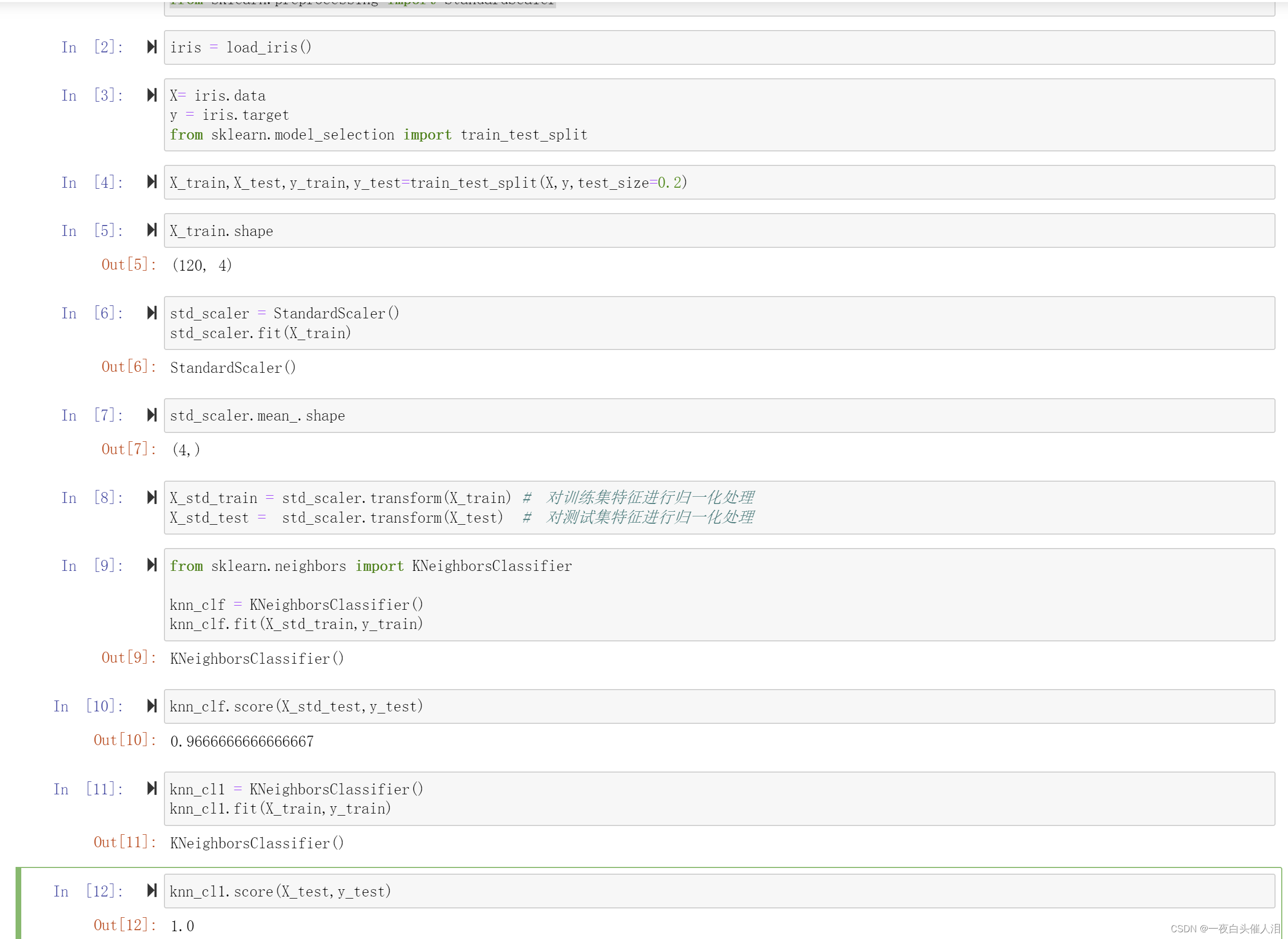
X= iris.data
y = iris.target
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2)
X_train.shape
std_scaler = StandardScaler()
std_scaler.fit(X_train)
std_scaler.mean_.shape
X_std_train = std_scaler.transform(X_train) # 对训练集特征进行归一化处理
X_std_test = std_scaler.transform(X_test) # 对测试集特征进行归一化处理
from sklearn.neighbors import KNeighborsClassifierknn_clf = KNeighborsClassifier()
knn_clf.fit(X_std_train,y_train)
knn_clf.score(X_std_test,y_test)
knn_cl1 = KNeighborsClassifier()
knn_cl1.fit(X_train,y_train)
knn_cl1.score(X_test,y_test)
四、knn算法总结
# knn: 天然可以解决分类的算法
# 思想简单,效果强大
# 缺点: 效率很低
# 缺点: 高度数据相关outlier
# 缺点: 预测的结果不具有可解释性
# 缺点: 维数灾难: 随着维度的增加,看似很相近的点,之间的距离会越来越大
五、线性回归
# 线性回归:判断数据的特征和目标值之间具有一定的线性关系
# 最简单的线性回归:样本的特征只有一个,用线性回归法进行预测,叫做简单线性回归
# 推广到样本特征有多个,多元线性回归
# 实现简单,是很多非线性模型的基础
# 结果具有很强的解释性,可以学习到一些真实世界中的知识
# np.sum(|y` - y| )
# np.sum((y` - y)**2)
# 损失函数
import numpy as np
import matplotlib.pyplot as plt
x = np.array([1,2,3,4,5])
y = np.array([1,3,2,3,5])
plt.scatter(x,y)
plt.axis([0,6,0,6])
plt.show()
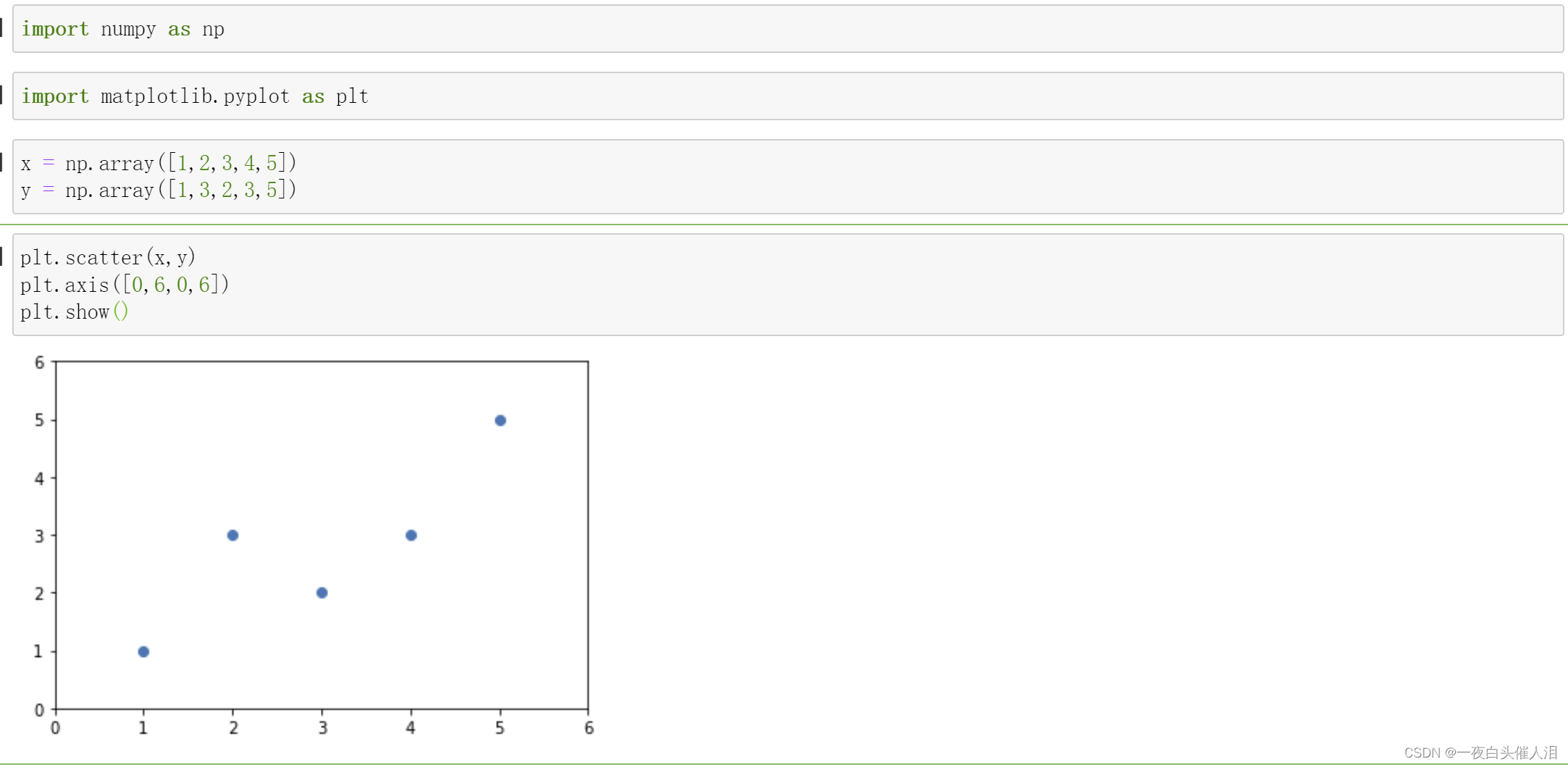
# y = a*x+b 需要计算出a和b
x_mean = np.mean(x)
y_mean = np.mean(y)
num = 0.0 # 分子
d = 0.0 # 分母
for x_i,y_i in zip(x,y):num += (x_i-x_mean)*(y_i-y_mean)d += (x_i-x_mean)**2
a = num/d
b = y_mean-a*x_mean
a
b
y_hat = a * x +b
plt.plot(x,y_hat,color='r')
plt.scatter(x,y)
plt.axis([0,6,0,6])
plt.show()
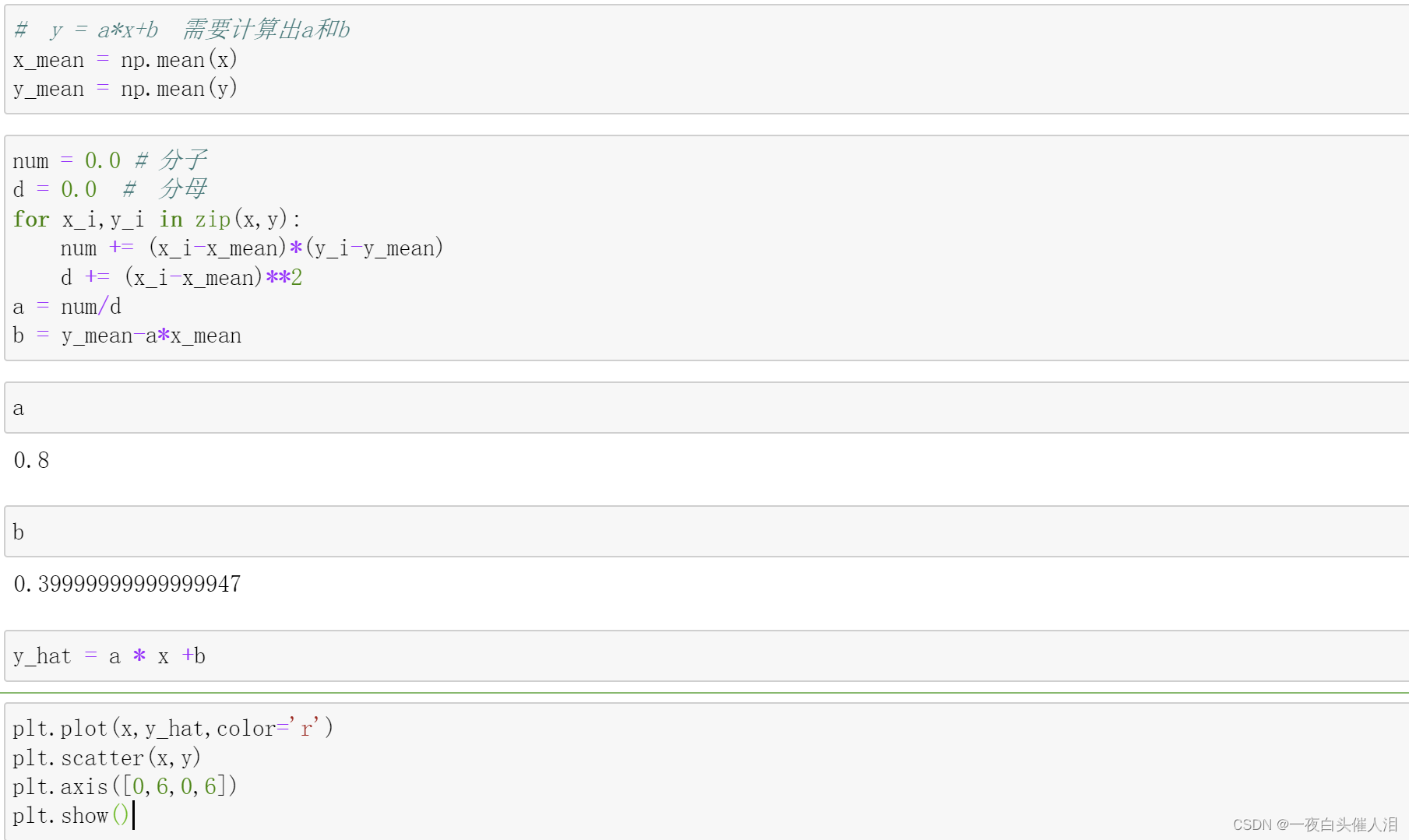

x_predict = 3.5
a*x_predict+b
%run MechainLearning/SimpleLinearRegression.py
lin_reg = SimpleLinearRegression()
lin_reg.fit(x,y)
lin_reg.predict()

SimpleLinearRegression.py
import numpy as npclass SimpleLinearRegression:def __init__(self):self.a_ = Noneself.b_ = Noneself.x_mean = Noneself.y_mean = Nonedef fit(self, x_train, y_train):self.x_mean = np.mean(x_train)self.y_mean = np.mean(y_train)num = 0.0 # 分子d = 0.0 # 分母for x_i, y_i in zip(x_train, y_train):num += (x_i - self.x_mean) * (y_i - self.y_mean)d += (x_i - self.x_mean) ** 2self.a = num / dself.b = self.y_mean - self.a * self.x_meanreturn selfdef predict(self, x_test):return self.a * x_test + self.bmoduel_selection.py
import numpy as npdef train_test_split(X, y, test_ratio=0.2, random_state=None):if random_state:np.random.seed(random_state)shuffle_indexs = np.random.permutation(len(X))test_ratio = test_ratiotest_size = int(len(X) * test_ratio)test_indexs = shuffle_indexs[:test_size]train_indexs = shuffle_indexs[test_size:]X_train = X[train_indexs]y_train = y[train_indexs]X_test = X[test_indexs]y_test = y[test_indexs]return X_train, X_test, y_train, y_testfrom sklearn.neighbors import KNeighborsClassifierknn = KNeighborsClassifier()draft.py
import randomrandom.seed(666)
print(random.random())
print(random.random())
print(random.random())def random(num):pass六、简单线性回归
# 前提:认为数据具有一定的线性关系
# 希望找到一条最佳拟合的直线方程,只针对简单线性回归(只有一个特征值)
# y = ax+b 对于每一个样本点,在这个直线方程上都有一个预测值,预测值和真实值有一定的差距
# 我们希望这些样本到直线方程的差距之和最小# 如何计算这些差距? |y-y~| sqrt((y-y~)**2)
# loss function 损失函数 希望损失函数达到最小值
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt
x = np.array([1,2,3,4,5])
y = np.array([1,3,2,3,5])
plt.scatter(x,y)
plt.axis([0,6,0,6])
plt.show()
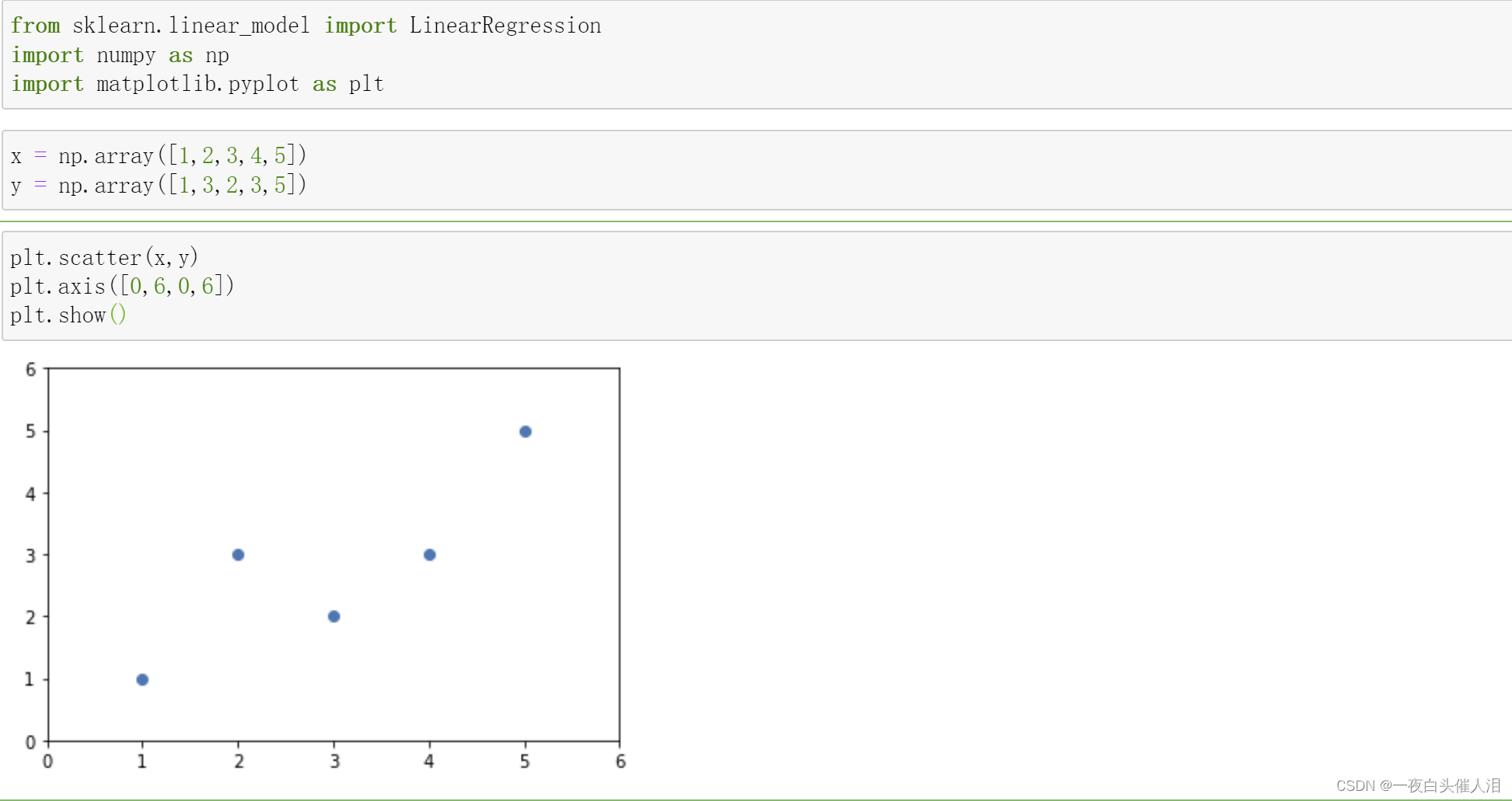
lin_reg = LinearRegression()
lin_reg.fit(x.reshape(-1,1),y)
lin_reg.coef_ # 系数
lin_reg.intercept_ # 截距
plt.scatter(x,y)
plt.plot(x,lin_reg.predict(x.reshape(-1,1)),color='r')
plt.axis([0,6,0,6])
plt.show()

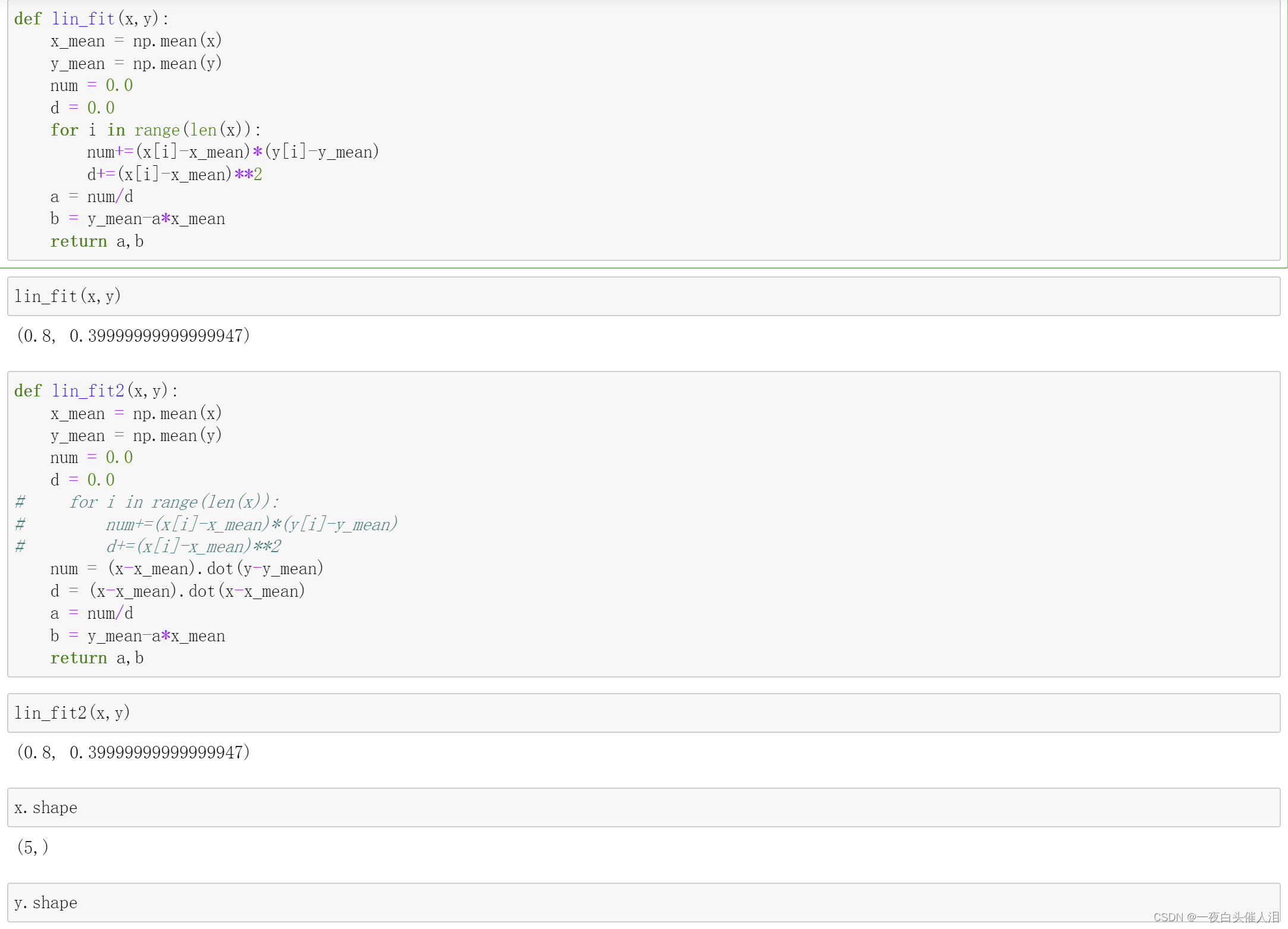
def lin_fit(x,y):x_mean = np.mean(x)y_mean = np.mean(y)num = 0.0d = 0.0for i in range(len(x)):num+=(x[i]-x_mean)*(y[i]-y_mean)d+=(x[i]-x_mean)**2a = num/db = y_mean-a*x_meanreturn a,b
lin_fit(x,y)
def lin_fit2(x,y):x_mean = np.mean(x)y_mean = np.mean(y)num = 0.0d = 0.0
# for i in range(len(x)):
# num+=(x[i]-x_mean)*(y[i]-y_mean)
# d+=(x[i]-x_mean)**2num = (x-x_mean).dot(y-y_mean)d = (x-x_mean).dot(x-x_mean)a = num/db = y_mean-a*x_meanreturn a,b
lin_fit2(x,y)
x.shape
y.shape
七、线性回归模型评优
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as pltx = np.array([1,2,3,4,5])
y = np.array([1,3,2,3,5])lin_reg = LinearRegression()
lin_reg.fit(x.reshape(-1,1),y)lin_reg.score(x.reshape(-1,1),y)

线性回归模型中的误差计算
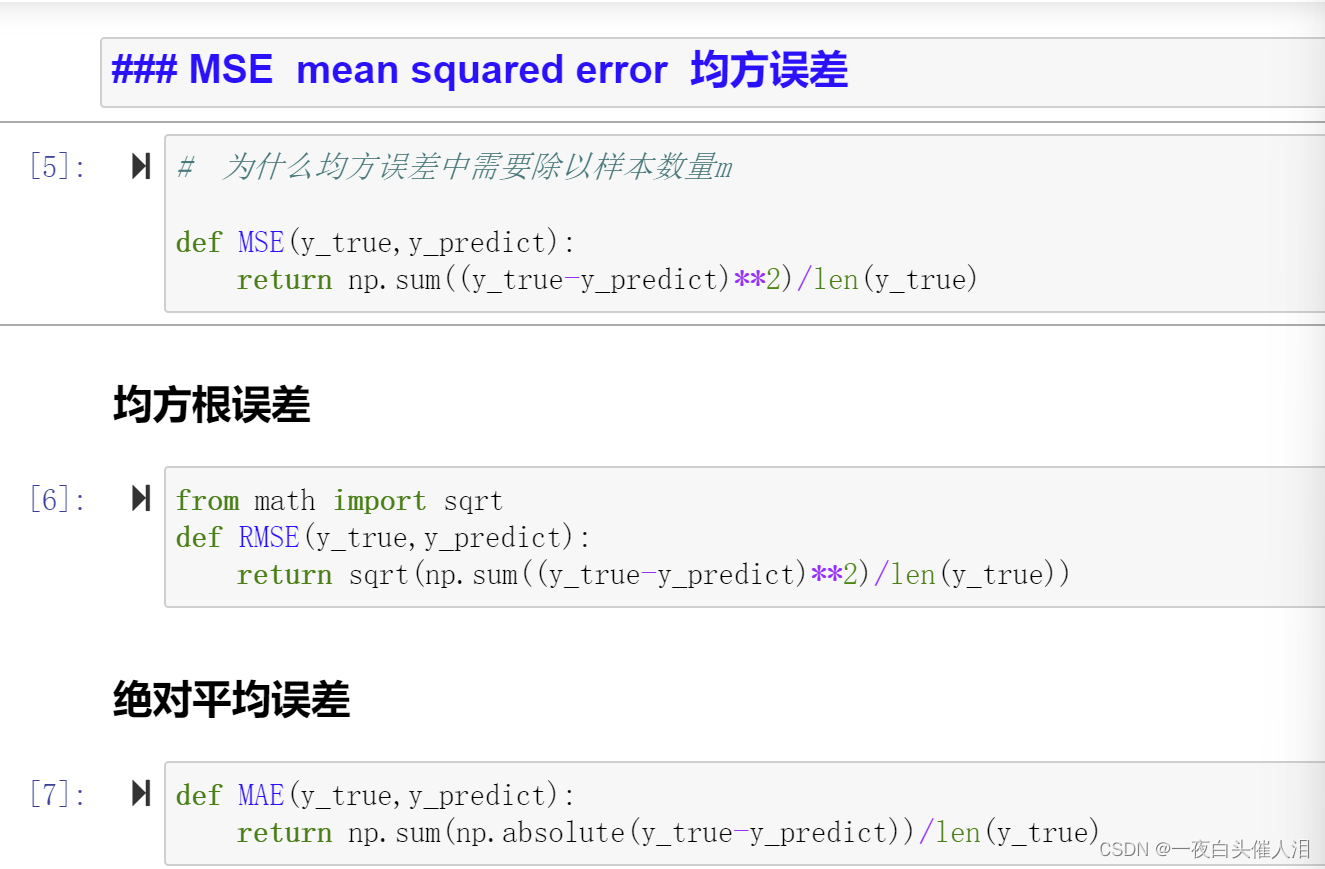
MSE mean squared error 均方误差
# 为什么均方误差中需要除以样本数量m def MSE(y_true,y_predict):return np.sum((y_true-y_predict)**2)/len(y_true)
均方根误差
from math import sqrt
def RMSE(y_true,y_predict):return sqrt(np.sum((y_true-y_predict)**2)/len(y_true))
绝对平均误差
def MAE(y_true,y_predict):return np.sum(np.absolute(y_true-y_predict))/len(y_true)
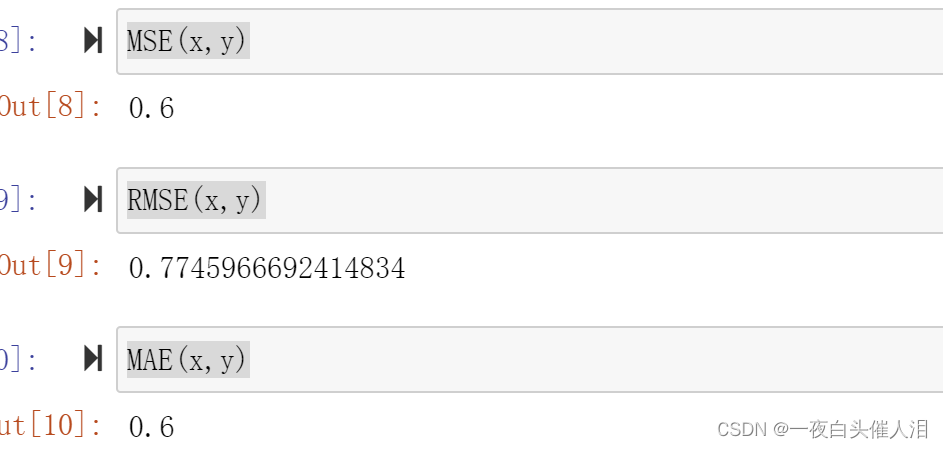
MSE(x,y)
RMSE(x,y)
MAE(x,y)
from sklearn.metrics import mean_squared_error,mean_absolute_error
mean_squared_error(x,y)
mean_absolute_error(x,y)
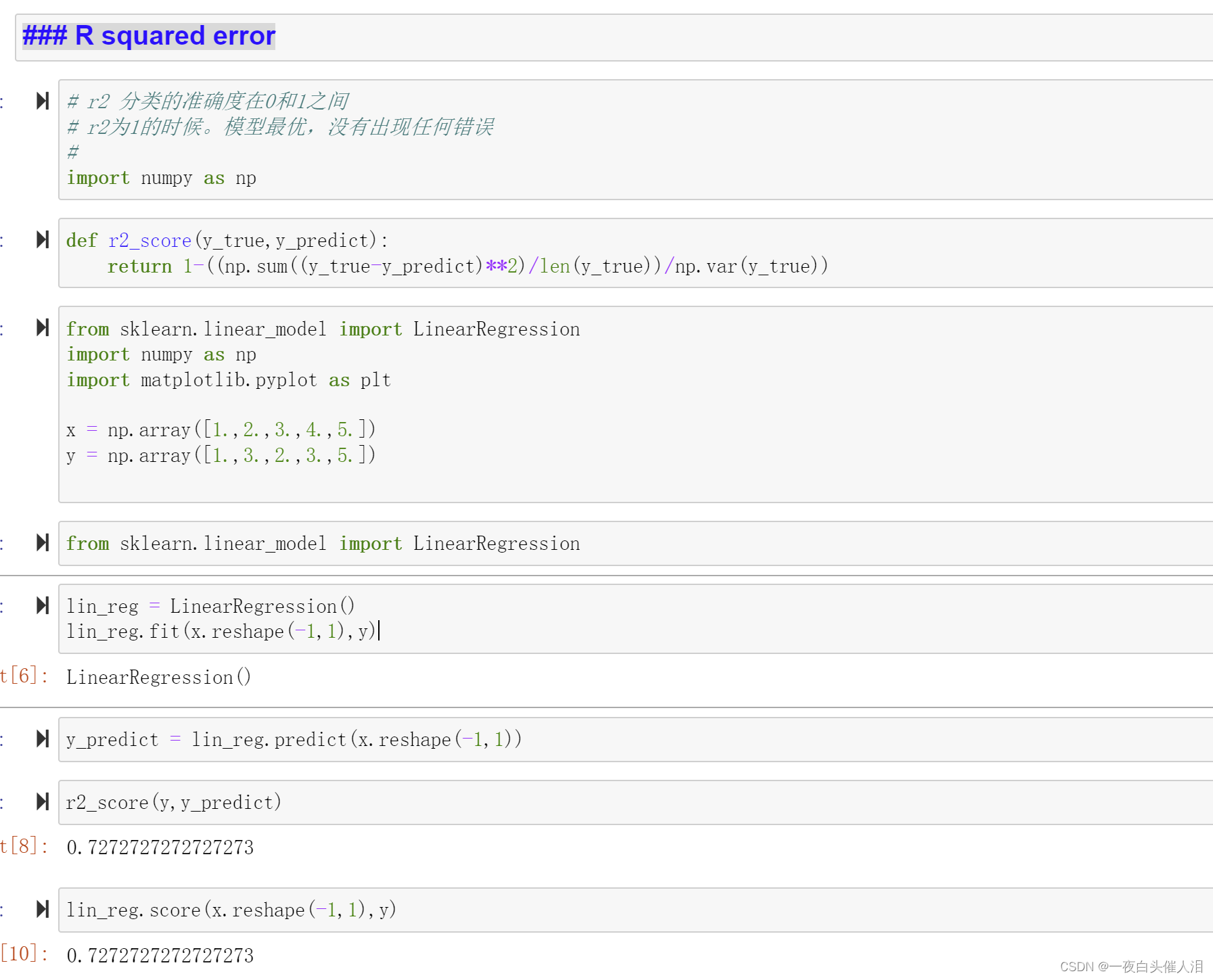
def r2_score(y_true,y_predict):return 1-MSE(y_true,y_predict)/np.var(y_true)
r2_score(x,y)

R squared error
八、多线线性回归
# 特征值不止一个,叫做多元线性回归
# 通过对矩阵进行转换,加一个x0维度,可以得到求出两个矩阵点乘的最小值问题
# 得到西塔的正规方程解,带入x和y就可以求出西塔
# 西塔是一个n+1 * 1 的矩阵
# 西塔0代表截距,西塔除第一个以外的元素代表系数
from sklearn.datasets import load_boston
boston = load_boston()
print(boston.DESCR)
boston.feature_names
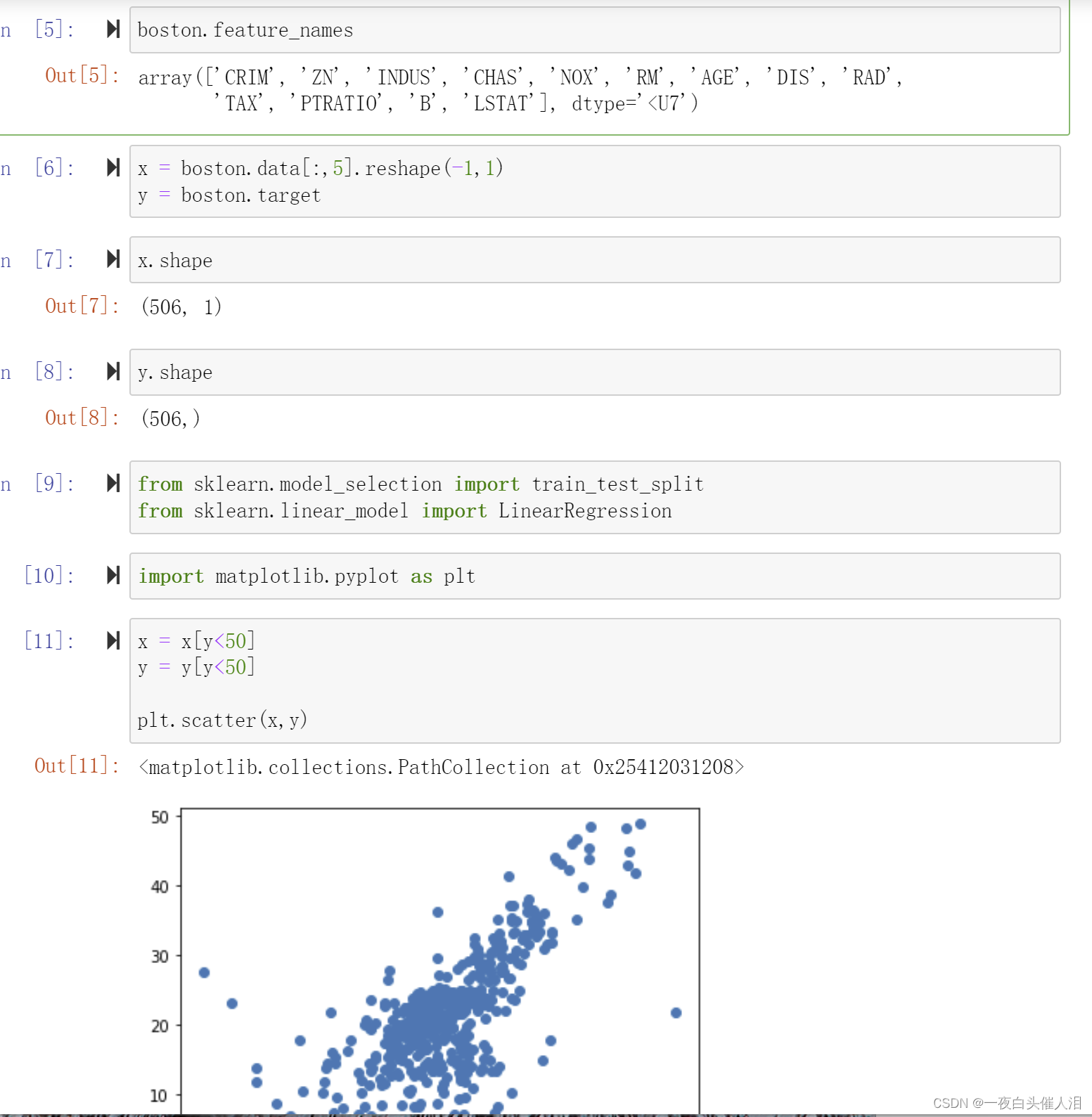
x = boston.data[:,5].reshape(-1,1)
y = boston.target
x.shape
y.shape
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
x = x[y<50]
y = y[y<50]plt.scatter(x,y)
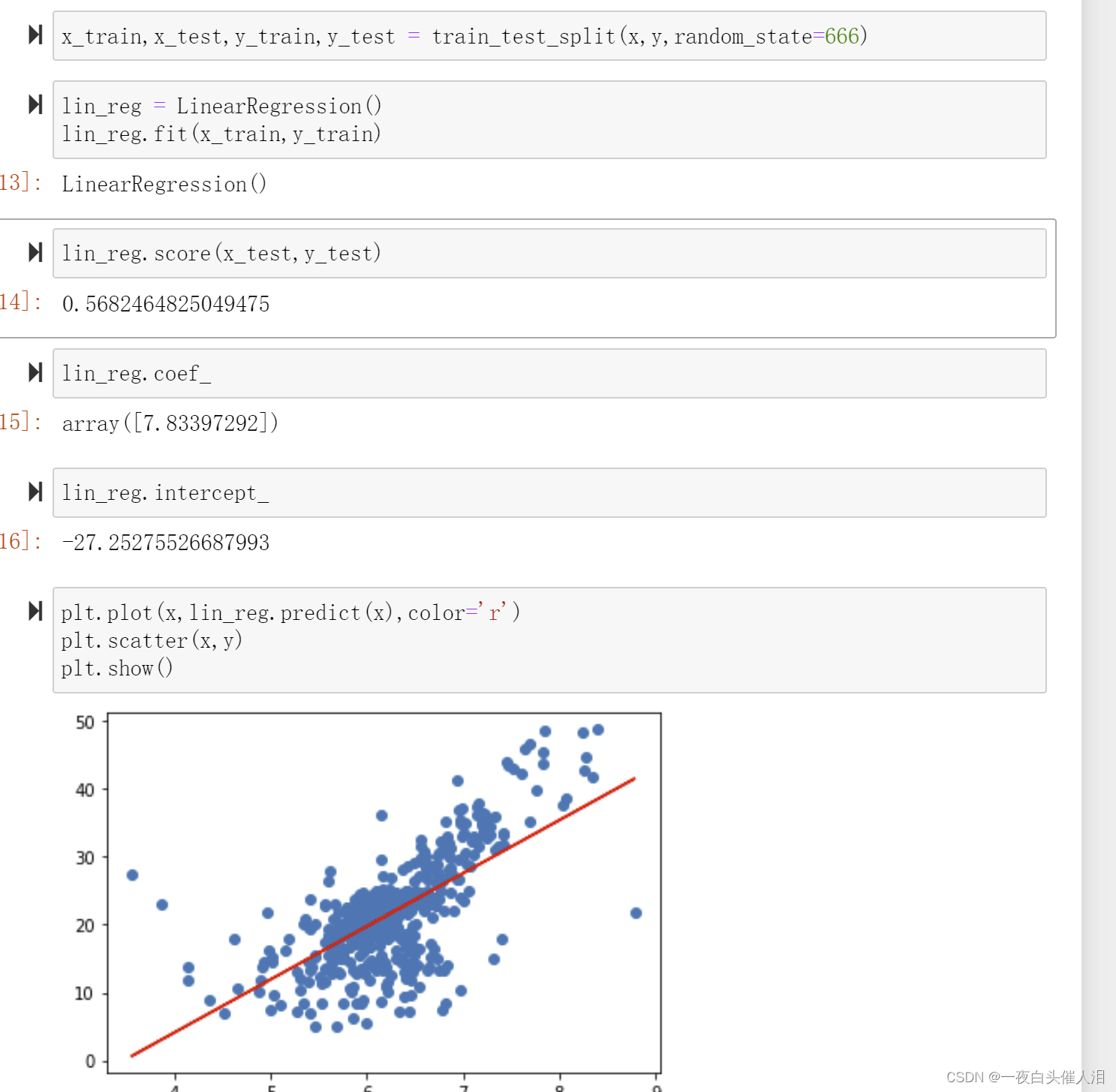


from spectral import *
from scipy.io import loadmat#读取数据并显示
input_image = loadmat('dc.mat')['imggt']
input_image_gt = loadmat('dc.mat')['imggt'][1,:,:]
v = imshow(input_image_gt)
v1 = imshow(input_image)
# principal_components计算图像数据的主组件,并返回一个主组件中的平均值、协方差、特征值和特征向量
pc = principal_components(input_image)
v2 = imshow(pc.cov)
#显示协方差矩阵 白色 强正协方差,深色 强负协方差,灰色 协方差接近于0
#保留至少99.9%的总图像方差
pc_0999 = pc.reduce(fraction = 0.99)
pc_0999.eigenvalues
#获取特征值
len(pc_0999.eigenvalues)#特征值数组长度为270
img_pc = pc_0999.transform(input_image)
v = imshow(img_pc[:,:,:3],stretch_all = True)
相关文章:

机器学习~从入门到精通(二)线性回归算法和多元线性回归
为什么要做数据归一化 一、数据归一化: 1.最值归一化 2.均值方差归一化import numpy as npX np.random.randint(1,100,size100) X X.reshape(-1,2) X.shape X np.array(X,dtypefloat) X[:,0] (X[:,0]-np.min(X[:,0]))/(np.max(X[:,0])-np.min(X[:,0])) X[:,1]…...

IPv6组播--PIM
IPv6组播路由协议 PIM(IPv6)作为一种IPv6网络中的组播路由协议,主要用于将网络中的组播数据流引入到有组播数据请求的组成员所连接的路由器上,从而实现组播数据流的路由查找与转发。 PIM(IPv6)协议包括PIM-SM(IPv6)和PIM-DM(IPv5)两种模式 IPv6组播协议定义 PIM(…...
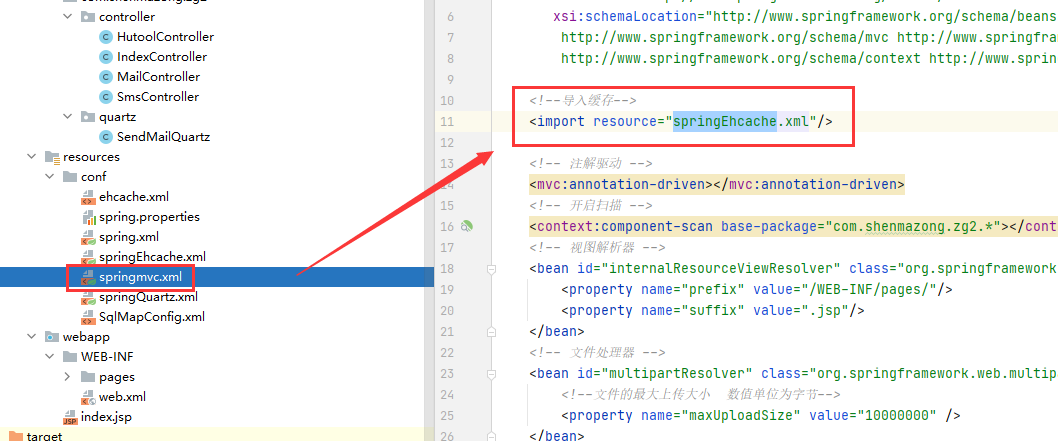
如何在Spring Boot中使用EhCache缓存
1、EhCache介绍 在查询数据的时候,数据大多来自于数据库,我们会基于SQL语句与数据库交互,数据库一般会基于本地磁盘IO将数据读取到内存,返回给Java服务端,我们再将数据响应给前端,做数据展示。 但是MySQL…...

PDF 文档解除密码
PDF 文档解除密码 1. 文件 -> 文档属性 -> 安全 -> 文档限制摘要2. PDF365References 1. 文件 -> 文档属性 -> 安全 -> 文档限制摘要 密码保护《算法设计与分析基础_第3版.pdf》 2. PDF365 https://www.pdf365.cn/ 免费功能 -> PDF 去密码 开始去除 Re…...

React16源码: React中的expirationTime过期时间的计算源码实现
expirationTime 的计算方式 先看expirationTime相关的源代码,这里是异步的计算方式,它会有一个过期时间异步任务优先级比较低,可以被打断,防止一直被打断导致不能执行,所以React给它设置了 expirationTime 过期时间也…...

程序设计语言的分类
编译与解释 编译型 将源代码转换成目标代码,通常源代码是高级语言代码,目标代码是机器语言代码,执行编译的计算机程序称为编译器。 eg:java 好处:对于相同的源代码编译产生的目标代码执行速度更快,目标代码不需要编译…...
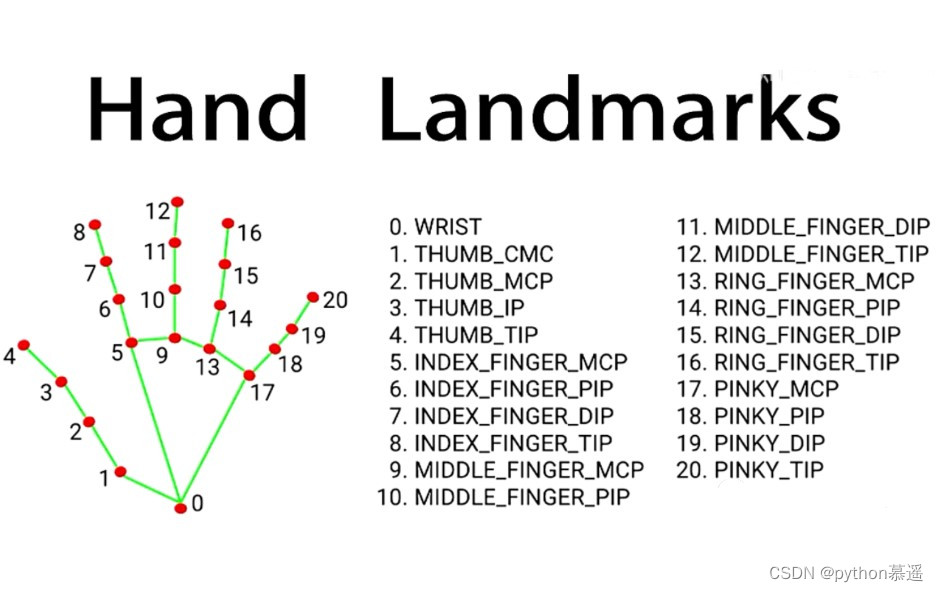
Python轻松实现炫酷的手势检测
大家好,今天分享一个非常有意思且十分简单的python库——mediapipe库。该库集成了大量的深度学习模型,短短几行代码,就可以快速实现一个炫酷的实例,本文就以手势检测为例,展示一下这个强大的开源库。 mediapipe由Goog…...
什么是信噪比
大家好,今天给大家介绍什么是信噪比,文章末尾附有分享大家一个资料包,差不多150多G。里面学习内容、面经、项目都比较新也比较全!可进群免费领取。 “信噪比”是电子技术中经常用到的一个词组,知道它的确切含义有一定意…...
学习redis有效期和数据类型
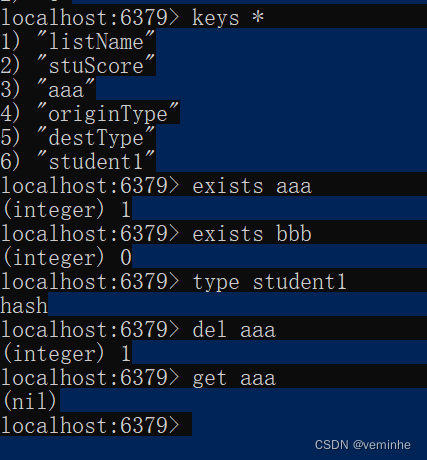
1、安装redis和连接redis 参考:ubuntu安装单个redis服务_ubuntu redis单机版安装-CSDN博客 连接redis:redis-cli.exe -h localhost -p 6379 -a 123456 2、Redis数据类型 以下操作我们在图形化界面演示。 2.1、五种常用数据类型介绍 Redis存储的是key…...

【linux】进程管理
前言 linux也有类似于windows的任务管理器的功能,我们也可以通过这个功能查看当前的进程情况。 语法 ps [-e] [-f] -e显示所有进程 -f显示完整的信息 我们可以直接用-ef来简化指令。 案例演示 信息过滤 但是如果我们直接这么输入的话,可以看到他回复…...

k8s operator从0到1实践
文章目录 环境准备一个k8s集群开发工具包mac安装 实践初始化operator项目核心逻辑编写测试验证验证 部署 参考 环境准备 一个k8s集群 推荐使用docker-desktop,本地单机集群 开发工具包 这里推荐使用脚手架工具kubebuilder 使用脚手架工具,能生成项目…...
【动态规划】dp多状态问题
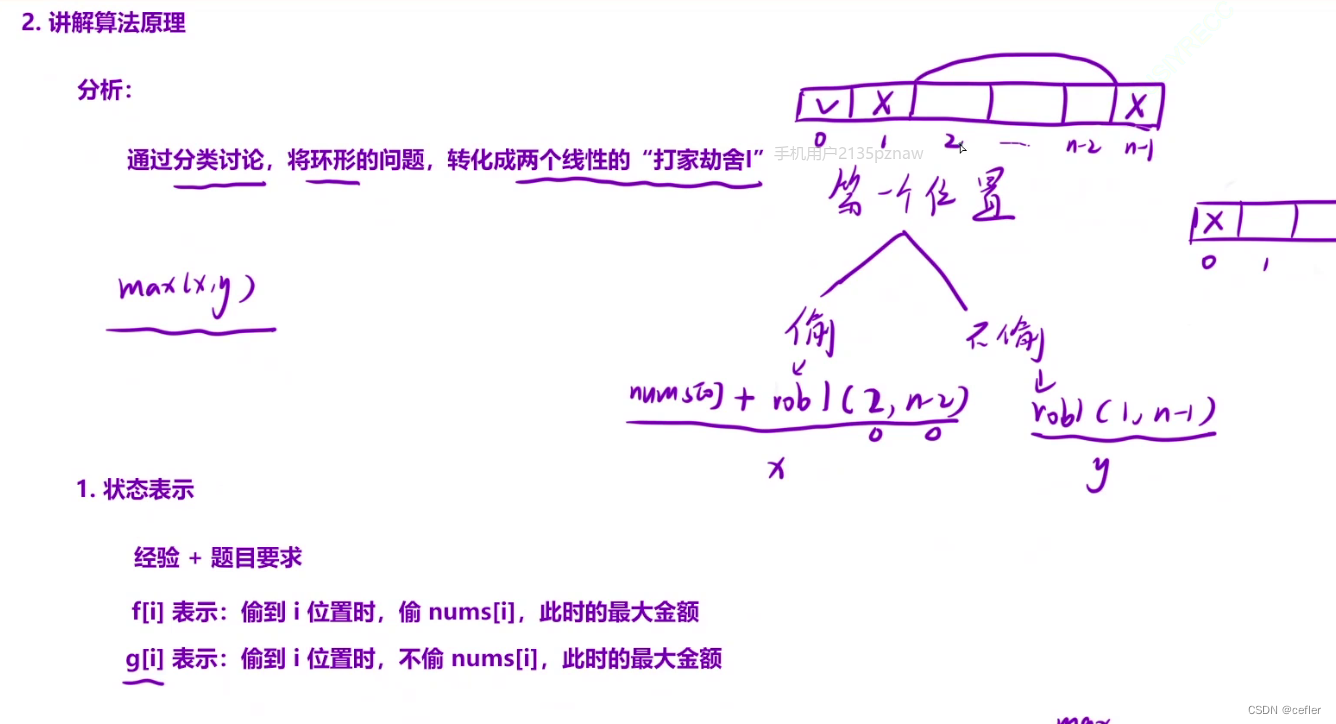
欢迎来到Cefler的博客😁 🕌博客主页:那个传说中的man的主页 🏠个人专栏:题目解析 🌎推荐文章:【LeetCode】winter vacation training 目录 👉🏻按摩师👉&…...
docker安裝gocd-server,并配置gitlab授权登录
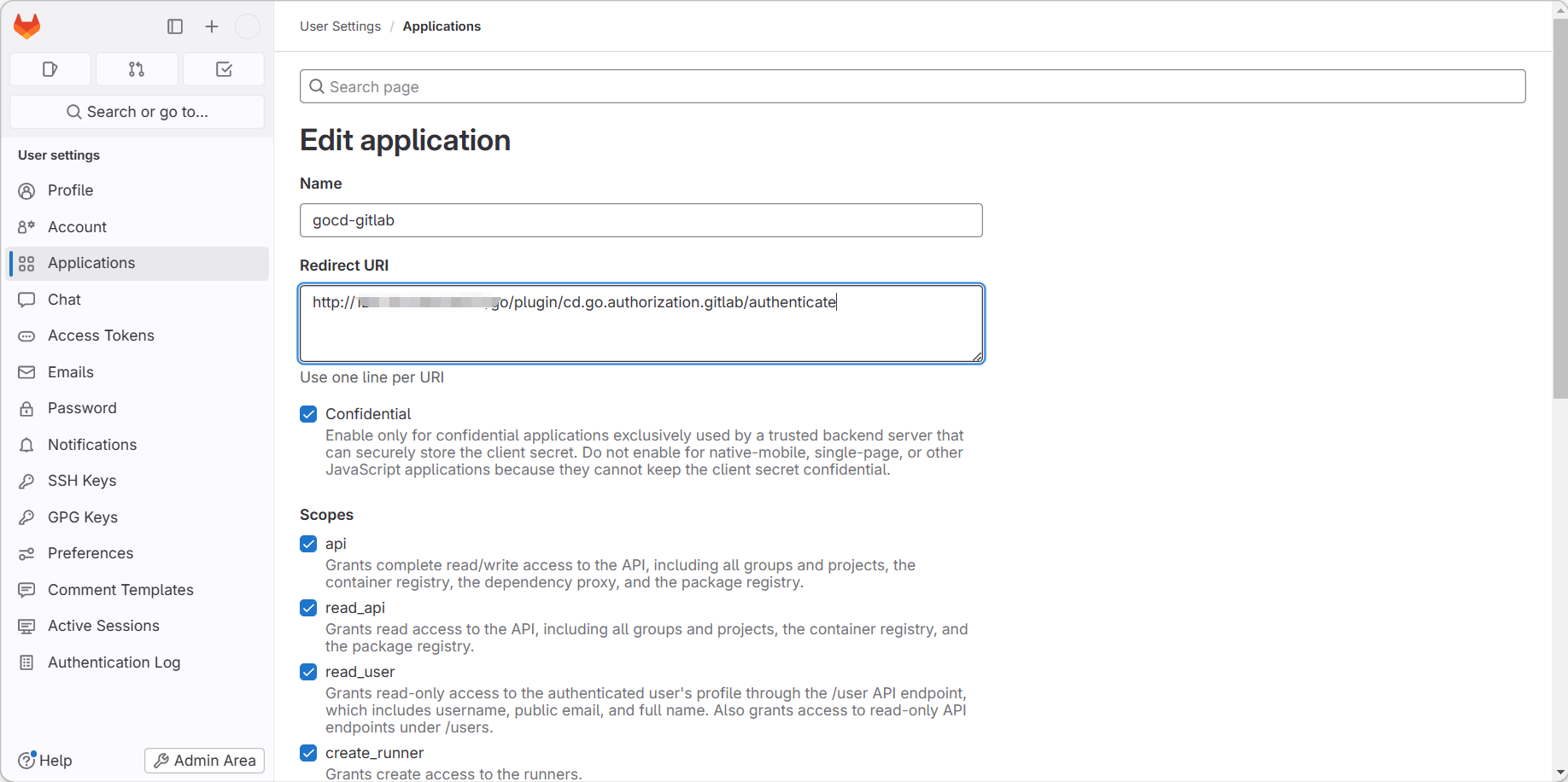
gocd的地址:Installing GoCD server on Windows | GoCD User Documentation gocd文档:GitHub - gocd/docker-gocd-server: Docker server image for GoCD 一、docker拉取gocd镜像 #拉取server镜像 docker pull gocd/gocd-server:v21.1.0docker pull g…...
使用pygame实现简单的烟花效果
import pygame import sys import random import math# 初始化 Pygame pygame.init()# 设置窗口大小 width, height 800, 600 screen pygame.display.set_mode((width, height)) pygame.display.set_caption("Fireworks Explosion")# 定义颜色 black (0, 0, 0) wh…...
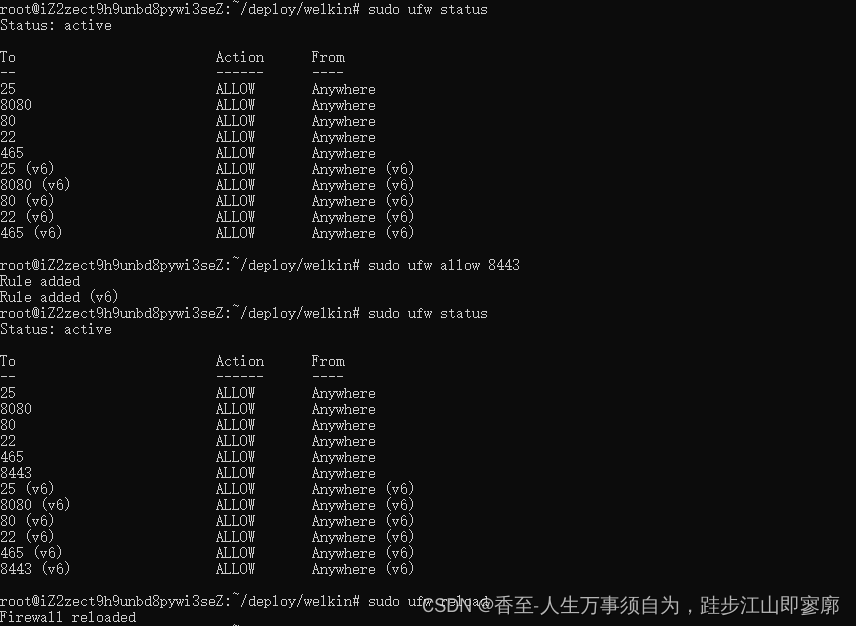
ubantu系统运维命令,端口相关操作
1、使用sudo ufw status命令查看所有开放的端口,如下图: 2、使用命令sudo ufw allow 8443,打开端口8443.如下图: 3、使用 sudo ufw reload刷新端口配置,如下图:...

Java中的Stream API进阶使用
Java的Stream API是Java 8引入的一个强大的功能,它允许以声明性方式处理数据集合,例如过滤、映射、排序等。下面是一些Stream API的进阶使用: 自定义中间操作:你可以定义自己的中间操作,然后在Stream上使用它。例如&am…...
:从PBDB获取单个采集号的基本信息)
R语言【paleobioDB】——pbdb_collection():从PBDB获取单个采集号的基本信息
Package paleobioDB version 0.7.0 paleobioDB 包在2020年已经停止更新,该包依赖PBDB v1 API。 可以选择在Index of /src/contrib/Archive/paleobioDB (r-project.org)下载安装包后,执行本地安装。 Usage pbdb_collection (id, ...) Arguments 参数【…...
阿里云服务器的tcp端口无法访问(云服务厂家问题?)
问题->无法访问 阿里云服务器的tcp端口 最近一台阿里云服务器的一个端口61616无法访问,在服务器内用外网地ip发现无法访问,用内网ip访问是正常的,通过技术排查: 解决->无法访问 阿里云服务器的tcp端口 1 配置官网的安全组…...
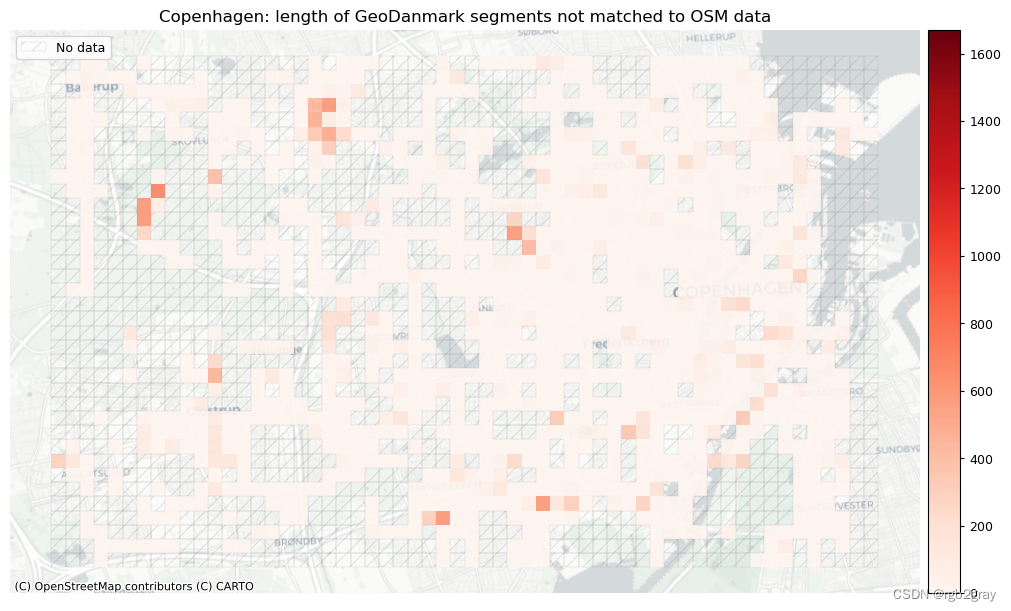
BikeDNA(九) 特征匹配
BikeDNA(九) 特征匹配 特征匹配采用参考数据并尝试识别 OSM 数据集中的相应特征。 特征匹配是比较单个特征而不是研究区域网格单元水平上的特征特征的必要前提。 方法 将两个道路数据集中的特征与其数字化特征的方式以及边缘之间潜在的一对多关系进行…...

vuex是什么?怎么使用?哪种功能场景使用它?
Vuex是Vue.js官方推荐的状态管理库,用于在Vue应用程序中管理和共享状态。它基于Flux架构和单向数据流的概念,将应用程序的状态集中管理,使得状态的变化更可追踪、更易于管理。Vuex提供了一个全局的状态树,以及一些用于修改状态的方…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...
