二分图带权最大匹配-KM算法详解
文章目录
- 零、前言
- 一、红娘再牵线
- 二、二分图带权最大完备匹配
- 2.1二分图带权最大匹配
- 2.2概念
- 2.3KM算法
- 2.3.1交错树
- 2.3.2顶标
- 2.3.3相等子图
- 2.3.4算法原理
- 2.3.5算法实现
- 三、OJ练习
- 3.1奔小康赚大钱
- 3.2Ants
零、前言
关于二分图:二分图及染色法判定-CSDN博客
关于二分图最大匹配:二分图最大匹配——匈牙利算法详解
一、红娘再牵线
红娘刚给上一批男女牵完线,便又遇到了3对男女(即3男3女),这次虽然比之前人少但也没那么好对付,每个男生都对若干个女生都有意思,每个女生也都对若干个男生都有意思,但是每对男女间的好感度不同,固然可以很容易配成3对情侣,但很难让每个人都满意,所以他们来请红娘出出主意。
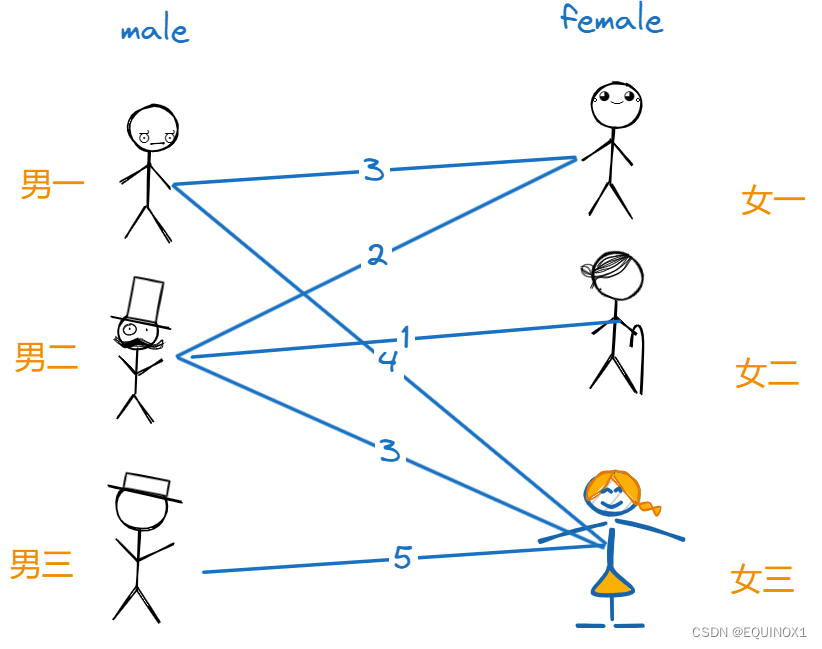
红娘了解了每对男女间的好感度后思索了一会便有了主意,她找来三个男生要求他们根据对三个女生亲密度给出对理想对象的期望值,要求给出的期望值不得小于其对任何一个女生的亲密度,女生那边则先不给出期望值。三个男生有些不好意思,便都只给出了和三个女生中的最大亲密度为期望值,于是又有了这样一张图:
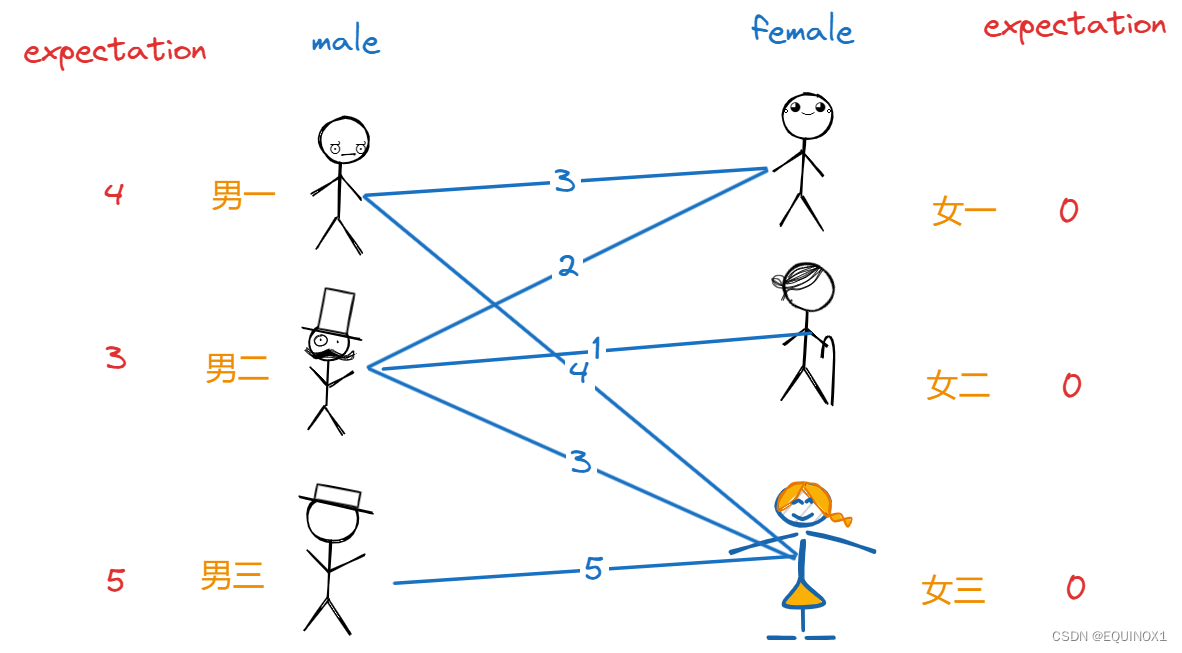
红娘打的什么算盘呢?她要让每个人都能有对象的情况下使得最终配对的情侣的亲密度之和最大,这是尽可能使每个人都满意的最好结局了。她要让最终每对情侣的期望值之和都等于其亲密值。
得到了男生们给出的期望值后,她先去给期望值之和恰好等于亲密度的男女配对(红线代表配对),男一和女三成功牵线:
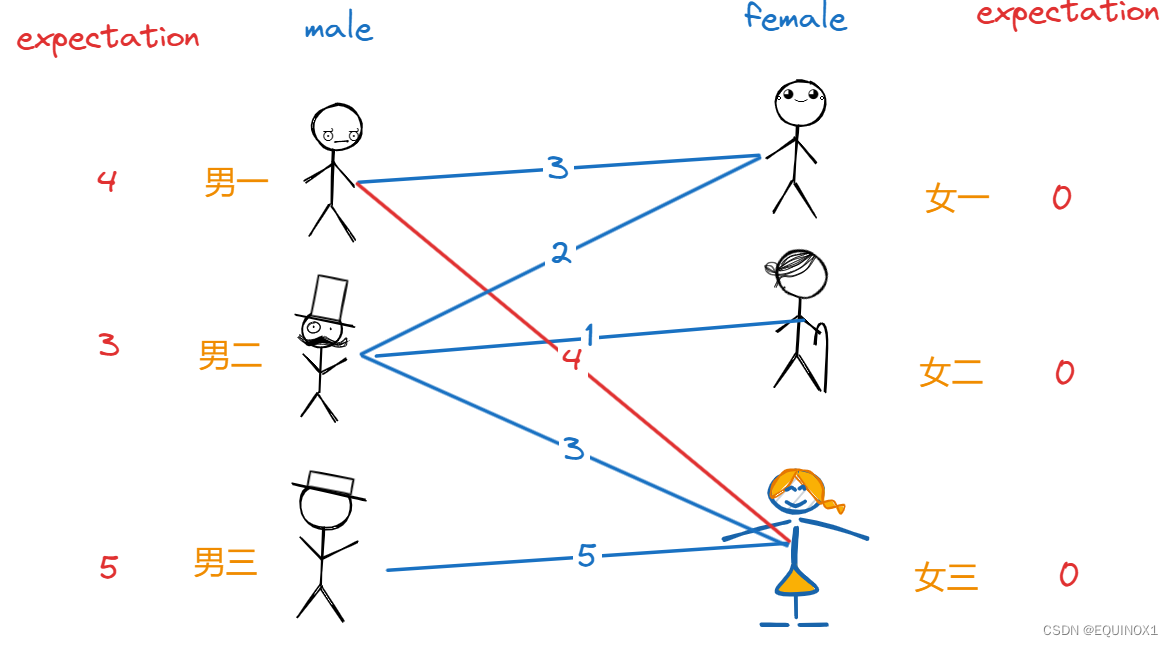
到了男二,发现符合条件的只有女三(期望值之和为亲密度),但是女三已经配对了,于是红娘让男一男二期望值都降低1,女三期望值提高1,如此一来男一女三仍符合条件,男二和女一也符合条件了,于是男儿女一牵线成功:
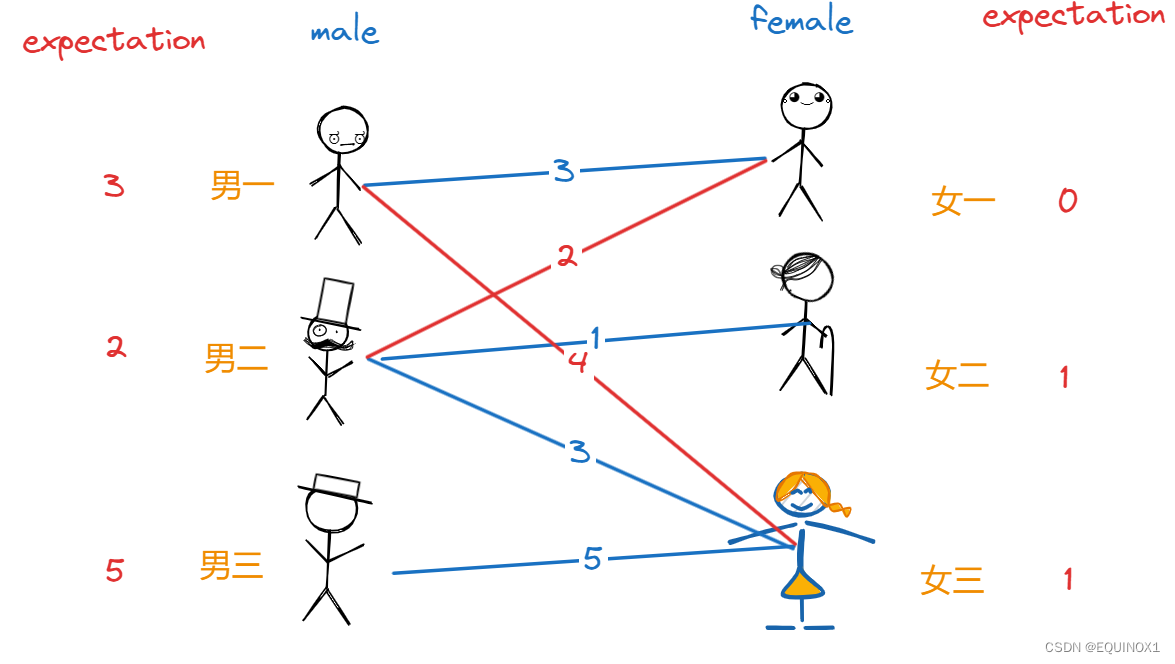
现在只剩男三落单了,对于她而言,只有女三有好感,但是二者期望值不符合条件,于是红娘先让男三降低1期望值:
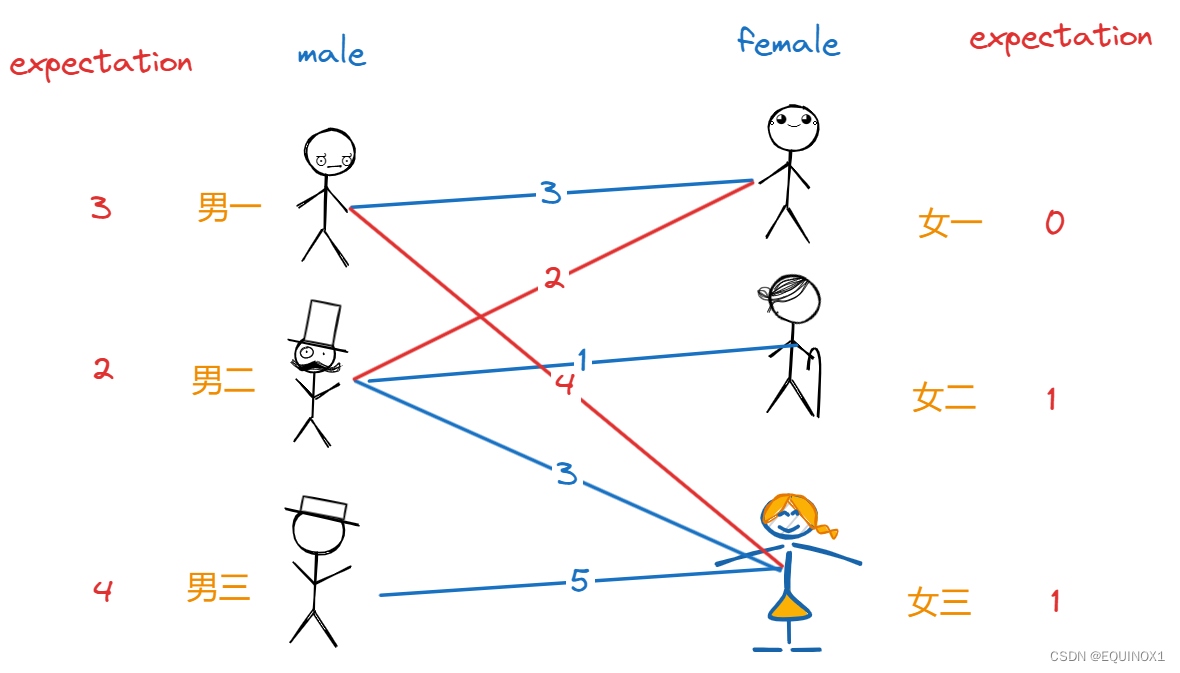
接着让男一、男二、男三都降低1期望值,女一、女三都提高1期望值,这样男一和女一符合条件可以配对,男二和女二符合条件可以配对,男三和女三符合条件可以配对:
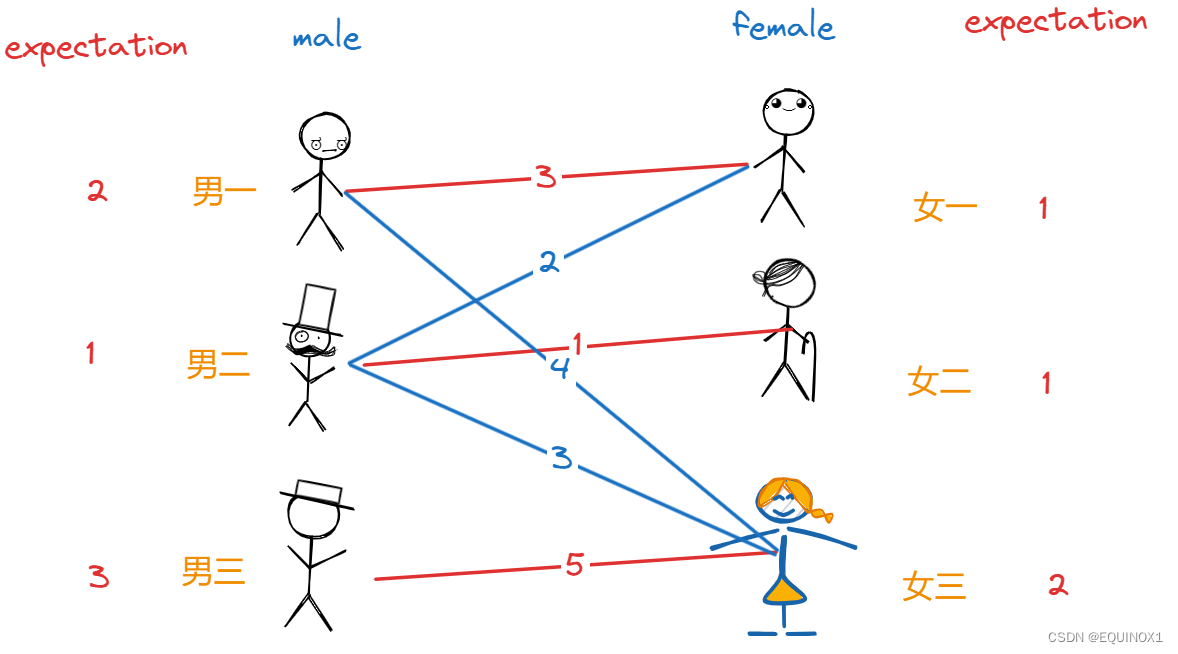
这样一来大家都有了归宿,且配对的男女的期望值之和恰为亲密度。显然,这是大家最满意的结局。
二、二分图带权最大完备匹配
2.1二分图带权最大匹配
给定一张二分图,二分图的每条边都带有一个权值。求出该二分图的一组最大匹配,使得匹配边的权值总和最大。这个问题称为二分图的带权最大匹配,也称二分图最优匹配。注意,二分图带权最大匹配的前提是匹配数最大,然后再最大化匹配边的权值总和。
2.2概念
如果一个二分图的带权最大匹配还是一个完备匹配,那么我们称其为二分图带权最大完备匹配,如引例”红娘再牵线“就是一个二分图带权最大完备匹配的例子。
二分图带权最大完备匹配是二分图带权最大匹配的子问题,能解决二分图带权最大匹配自然能解决二分图带权最大完备匹配。
对于二分图带权最大匹配我们通用方法是费用流,其自然也可以解决二分图带权最大完备匹配,也是我们最常用的方法,当然,对于二分图带权最大完备匹配有一专门解决方法——KM算法。
2.3KM算法
KM算法是对匈牙利算法的改造,我们从匈牙利算法入手,分析如何改造得以求解二分图带权最大完备匹配问题。
2.3.1交错树
在匈牙利算法中,如果从某个左部节点出发寻找匹配失败,那么在DFS的过程中,所有访问过的节点,以及为了访问这些节点而经过的边,共同构成一棵树。
这棵树的根是一个左部节点,所有叶子节点也都是左部节点(因为最终匹配失败了),并且树上第1,3,5,… 层的边都是非匹配边,第2,4,6,…层的边都是匹配边。因此,这棵树被称为交错树。
2.3.2顶标
亦即”顶点标记值“,在二分图中,给第i(1 <= i <= n)个左部节点一个整数值la[i],给第j(1 <= j <= n)个右部节点一个整数值lb[j]。同时满足:∀i,j,la[i] + lb[j] >= w[i][j],其中w[i][j]为第i个左部节点和第j个右部节点之间的边权(没有边权时设为负无穷),这些整数值la[i]、lb[j]称为节点的顶标。
2.3.3相等子图
二分图中所有节点 和 满足la[i] + lb[j] = w[i][j]的边构成的子图,称为二分图的相等子图。
定理:
若相等子图中存在完备匹配,则这个完备匹配就是二分图的带权最大匹配。
证明十分容易:
在相等子图中,完备匹配的边权之和等于Σ(la[i] + lb[j]),即所有顶标之和。因为顶标满足Vi,j, la[i] + lb[j] ≥ w(i,j),所以在整个二分图中,任何一组匹配的边权之和都不可能大于所有顶标的和。
2.3.4算法原理
KM算法的基本思想就是,先在满足∀i,j, la[i] + lb[j] ≥ w[i][j]的前提下,给每个节点随意赋值一个顶标, 然后采取适当策略不断扩大相等子图的规模,直至相等子图存在完备匹配。例如,我们可以赋值la[i] = max(w[i][j]),lb[j] = 0
对于一个相等子图,我们用匈牙利算法求它的最大匹配。若最大匹配不完备,则说明一定有一个左部节点匹配失败。该节点匹配失败的那次DFS形成了一棵交错树,记为T。
我们要找到相等子图中的完备匹配,此时失败说明相等子图中的边没有全部包含进来,所以我们要对顶标进行调整,使得相等子图得到扩充。
对于交错树中的边无非两种:
- la[i] + lb[j] = w[i][j]的匹配边(这也是和匈牙利不同的一点),那么对于匹配边我们不需要修改顶标和,可以使得左边减少Δ,右边增加Δ
- la[i] + lb[j] > w[i][j]的非匹配边(因为顶标和不小于权值,所以只能是大于),我们通过使左部节点减小Δ来减小顶标和,从而逼近权值
那么如何取Δ呢?
令Δ为min(la[i] + lb[j] - w[i][j]),w<i , j>为非匹配边,那么每次左部根节点匹配失败,进行一次调整都会使得相等子图增加至少一条边,而又不减少相等子图中的边。
2.3.5算法实现
- 初始化la,lb
- 对每个左部点进行修改后的匈牙利算法,找左部点的匹配右部点
- 匹配失败,就根据delta进行调整,再次匹配
- 对于匈牙利算法的修改:
- 只挑选顶标和为权值的边作为匹配边
- 利用顶标和大于权值的边维护delta
时间复杂度:O(N^4)
代码实现:
#define N 110
int w[N][N]; // 边权
int la[N], lb[N]; // 左、右部点顶标
bool va[N], vb[N]; // 左、右部点是否在交错树中
int match[N]; // 右部点的匹配点
int n, delta;
bool dfs(int u)
{va[u] = true; // 在交替树中for (int v = 1; v <= n; v++)if (!vb[v])if (la[u] + lb[v] - w[u][v] == 0){vb[v] = true; // 进入交替树if (!match[v] || dfs(match[v])){match[v] = u;return true; // 找到增广路}}else// 维护delta,同时避免非匹配边右部点进入交替树,保证非匹配边只有左部点顶标减小delta = min(delta, la[u] + lb[v] - w[u][v]);return false;
}int KM()
{memset(match, 0, sizeof(match)), memset(lb, 0, sizeof(lb));for (int i = 1; i <= n; i++){la[i] = w[i][1];for (int j = 2; j <= n; j++)la[i] = max(la[i], w[i][j]);}for (int i = 1; i <= n; i++)while (true) // 直到找到匹配{memset(va, 0, sizeof(va)), memset(vb, 0, sizeof(vb));delta = 1 << 30; // infif (dfs(i))break;for (int j = 1; j <= n; j++) // 修改顶标,扩充相等子图{if (va[j])la[j] -= delta;if (vb[j])lb[j] += delta;}}int ans = 0;for (int i = 1; i <= n; i++)ans += w[match[i]][i];return ans;
}
三、OJ练习
3.1奔小康赚大钱
Problem - 2255 (hdu.edu.cn)
很直白的KM算法板子题,直接跑板子即可
#include <iostream>
#include <cmath>
#include <cstring>
#include <vector>
#include <string>
#include <algorithm>
#include <functional>
#include <cmath>
using namespace std;
using pii = pair<int, int>;
#define sc scanf
#define N 310
#define int long long
#define precision 1e-9int w[N][N]; // 边权
int la[N], lb[N]; // 左、右部点顶标
bool va[N], vb[N]; // 左、右部点是否在交错树中
int match[N]; // 右部点的匹配点
int n, delta;
bool dfs(int u)
{va[u] = 1; // 在交替树中for (int v = 1; v <= n; v++)if (!vb[v])if (la[u] + lb[v] - w[u][v] == 0){vb[v] = 1; // 进入交替树if (!match[v] || dfs(match[v])){match[v] = u;return true; // 找到增广路}}elsedelta = min(delta, la[u] + lb[v] - w[u][v]);return false;
}int KM()
{memset(match, 0, sizeof(match)), memset(lb, 0, sizeof(lb));for (int i = 1; i <= n; i++){la[i] = w[i][1];for (int j = 2; j <= n; j++)la[i] = max(la[i], w[i][j]);}for (int i = 1; i <= n; i++)while (true) // 直到找到匹配{memset(va, 0, sizeof(va)), memset(vb, 0, sizeof(vb));delta = 1 << 30; // infif (dfs(i))break;for (int j = 1; j <= n; j++) // 修改顶标,扩充相等子图{if (va[j])la[j] -= delta;if (vb[j])lb[j] += delta;}}int ans = 0;for (int i = 1; i <= n; i++)ans += w[match[i]][i];return ans;
}signed main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);//freopen("in.txt", "r", stdin);while (cin >> n){for (int i = 1; i <= n; i++)for (int j = 1; j <= n; j++)cin >> w[i][j];cout << KM() << '\n';}return 0;
}
3.2Ants
3565 – Ants (poj.org)
一眼看去可能觉得要用到什么计算几何的知识,实际上如图:
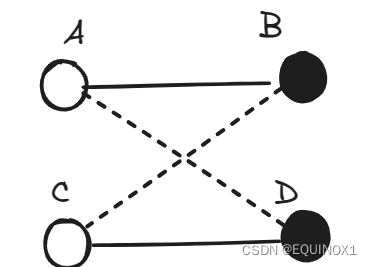
由三角形性质可知AD+BC > AB + CD,所以对于一对交叉的边一定可以转化为一对不交叉的边并且权值和变小
所以问题等价为求二分图带权 最小 完备匹配
那么我们把两两黑白点之间距离求出然后取反跑BMKM即可
但是对于这道题直接跑我们的板子会TLE的,因为我们最坏O(N^4)的时间复杂度在这道题刚好被卡了。
有一种比较懒省事的优化方法就是把全局的delta换成一个数组slack,来记录访问到的非匹配边的顶标和和边权之差
好处是slack只用在while循环外初始化一次然后就能用到while结束,而全局变量每次都要从inf开始
但这是个假优化,最坏仍为O(N^4)
正确优化为O(N^3)的方法是bfs优化,优化角度为从每次加入相等子图的那条边接着找增广路,这就需要我们记录上次失败时交错树的某些信息了。这里只给出slack假优化代码,bfs优化有兴趣可以查相关资料、博客,主要太懒感觉没什么用
#include <iostream>
#include <string>
#include <cstring>
#include <algorithm>
#include <climits>
#include <cmath>
using namespace std;
#define int long longconst double inf = 1e30;const double eps = 1e-6;const int N = 110;int n;pair<int, int> ant[N], tree[N];double dis(int i, int j)
{return sqrt(1.0 * (tree[i].first - ant[j].first) * (tree[i].first - ant[j].first) + (tree[i].second - ant[j].second) * (tree[i].second - ant[j].second));
}double la[N], lb[N], w[N][N];bool va[N], vb[N];int match[N];double upd[N];bool dfs(int u)
{va[u] = 1; // 在交替树中for (int v = 1; v <= n; v++)if (!vb[v])if (la[u] + lb[v] - w[u][v] < eps){vb[v] = 1; // 进入交替树if (!match[v] || dfs(match[v])){match[v] = u;return true; // 找到增广路}}elseupd[v] = min(upd[v], la[u] + lb[v] - w[u][v]);return false;
}void KM()
{memset(match, 0, sizeof(match)), memset(lb, 0, sizeof(lb));for (int i = 1; i <= n; i++){la[i] = w[i][1];for (int j = 2; j <= n; j++)la[i] = max(la[i], w[i][j]);}for (int i = 1; i <= n; i++){memset(upd, 0x3f, sizeof(upd));while (1) // 直到左部点找到匹配{memset(va, 0, sizeof(va)), memset(vb, 0, sizeof(vb));for (int i = 1; i <= n; i++)upd[i] = inf;if (dfs(i))break;double delta = inf;for (int j = 1; j <= n; j++)if (!vb[j])delta = min(delta, upd[j]);for (int j = 1; j <= n; j++) // 修改顶标{if (va[j])la[j] -= delta;if (vb[j])lb[j] += delta;}}}for (int i = 1; i <= n; i++)cout << match[i] << '\n';
}signed main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);while (cin >> n){for (int i = 1; i <= n; i++)cin >> ant[i].first >> ant[i].second;for (int i = 1; i <= n; i++)cin >> tree[i].first >> tree[i].second;for (int i = 1; i <= n; i++)for (int j = 1; j <= n; j++)w[i][j] = -dis(i, j);KM();}return 0;
}
相关文章:

二分图带权最大匹配-KM算法详解
文章目录 零、前言一、红娘再牵线二、二分图带权最大完备匹配2.1二分图带权最大匹配2.2概念2.3KM算法2.3.1交错树2.3.2顶标2.3.3相等子图2.3.4算法原理2.3.5算法实现 三、OJ练习3.1奔小康赚大钱3.2Ants 零、前言 关于二分图:二分图及染色法判定-CSDN博客 关于二分…...

Redis命令 - Sets命令组常用命令
Set集合,无序,一堆不重复值的组合。利用redis提供的set数据结构,可以存储一些集合性的数据。 使用场景:例如,实现如共同关注、共同喜好、二度好友等 1、SADD key member [member …] 向集合中添加一个或者多个成员 …...

DA14531-外设驱动篇-I2C通信应用
文章目录 1.I2C通信应用相关文件2.宏定义列表3.主要函数接口4.应用代码实例1.I2C通信应用相关文件 1)i2c.c和i2c.h(SDK文件) 2)app_I2cProtocol.c和app_I2cProtocol.h(用户应用文件) 2.宏定义列表 宏定义注解I2C_ADDRESSING_7B7-bit 地址I2C_ADDRESSING_10B10-bit 地址…...

Git仓库管理笔记
问题: hint: the same ref. If you want to integrate the remote changes, use Done 解决: 解决方法: 1、先使用pull命令: git pull --rebase origin master 2、再使用push命令: git push -u origin master...
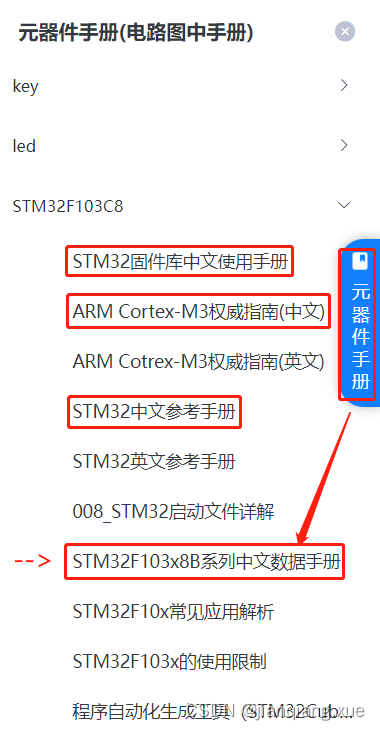
[嵌入式软件][入门篇] 搭建在线仿真平台(STM32)
文章目录 一、注册平台二、创建首个项目三、硬件介绍 一、注册平台 进入官方,进行注册: 在线仿真地址 二、创建首个项目 ① 新建项目 ② 搭建一个电路 ③ 用STM32F103搭建一个简单电路 ④ 进入编码界面 三、硬件介绍 红框是必看文档ÿ…...

设置5台SSH互免的虚拟机服务器配置
搭建一套集群虚拟机,往往都需要互免设置,过程很简单,避免以后再搭建还得网上搜索,我直接将这一个步骤写成笔记,记录下来,方便后续查阅。 步骤如下—— 1、准备五台机器 服务器名字服务器IPhadoop1192.16…...

深信服技术认证“SCCA-C”划重点:交付和运维体系
为帮助大家更加系统化地学习云计算知识,高效通过云计算工程师认证,深信服特推出“SCCA-C认证备考秘笈”,共十期内容。“考试重点”内容框架,帮助大家快速get重点知识。 划重点来啦 *点击图片放大展示 深信服云计算认证ÿ…...
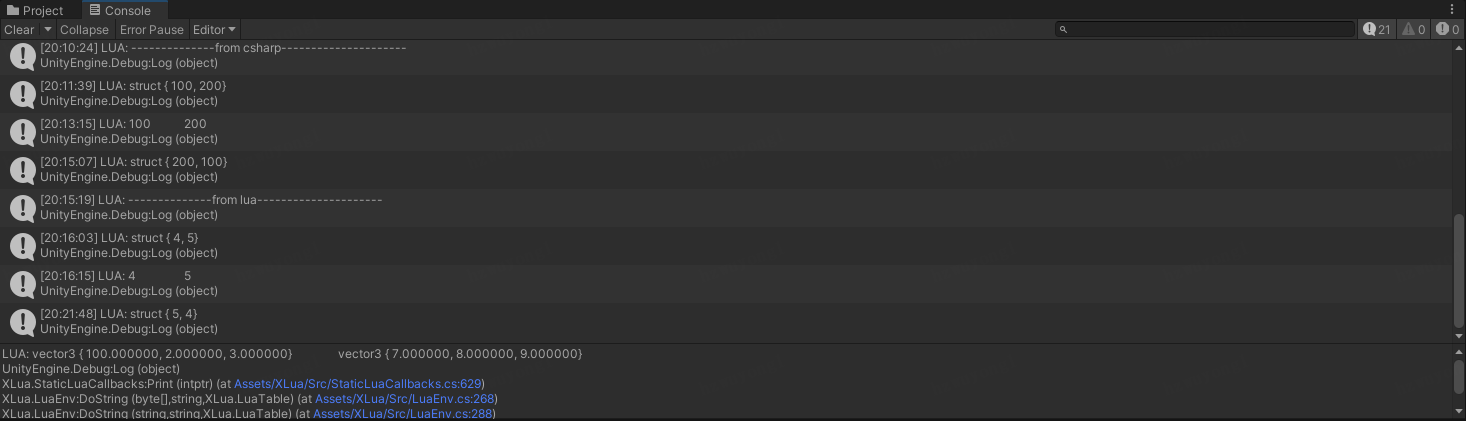
xlua源码分析(五) struct类型优化
xlua源码分析(五) struct类型优化 上一节我们分析了xlua是如何实现lua层访问C#值类型的,其中我们重点提到了xlua默认实现方式下,struct访问的效率问题。实际上,xlua还提供了两种优化的方式,可以大大提高str…...

iptables TEE模块测试小记
概述 因为公司项目需求,需要对服务器特定端口进行流量镜像,各种百度之后,发现TEE的模块,后来一番折腾,发现被转发的机器死活收不到数据,最后tcpdump一通了解到根源,博文记录,用以备…...

facebook广告怎么设置受众人群
在设置Facebook广告受众人群时,你可以遵循以下步骤: 打开广告创建工具,点击页面右上角的箭头并选择“创建广告”。选择广告目标,根据想要实现的目标创建广告。例如,想要让更多用户谈论你的主页和帖子,或者…...

MySQL夯实之路-MVCC机制深入浅出
多版本并发控制(MVCC,multiversion concurrency control) MVCC用更加灵活的方式处理并发,实现了读不加锁,读写不冲突。保证了事务的隔离性(可重复读),避免了不可重复读问题。 数据…...
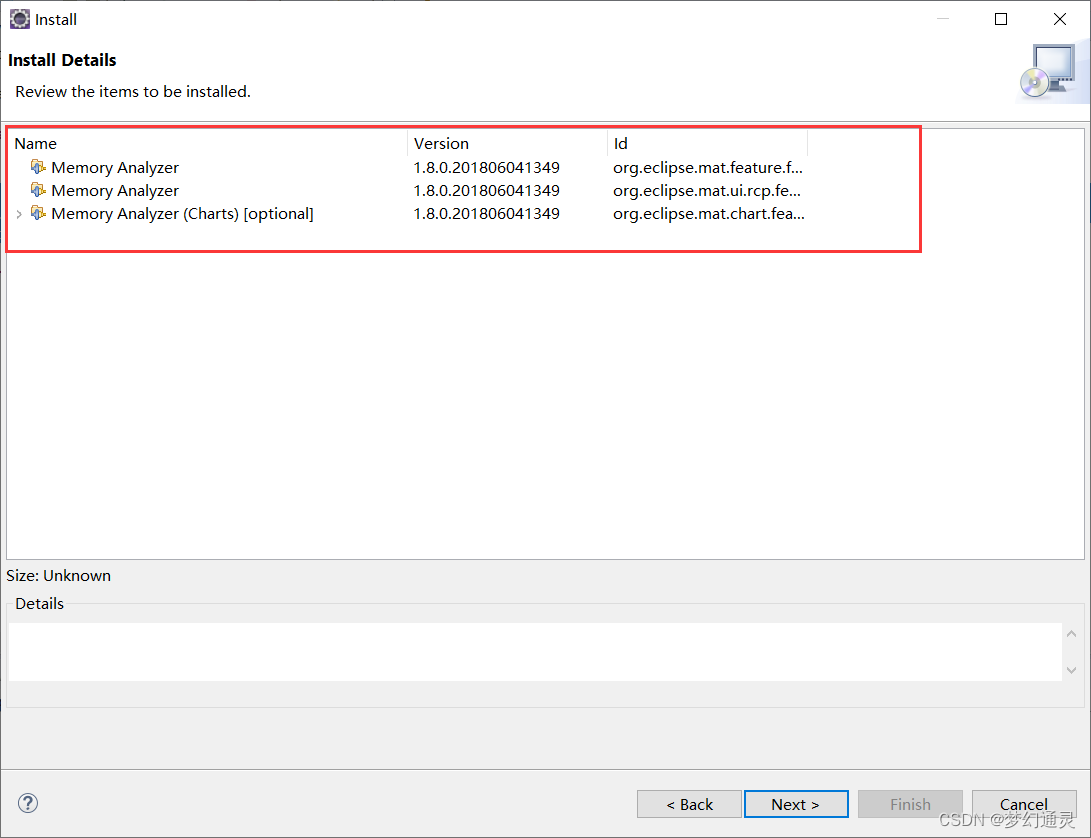
Java线上问题堆栈排查分析
最近线上出现类似内存溢出问题,需要排查具体原因,记录过程,方便备查。 一、数据抓取 在启动参数中添加参数,可参照以下设置。 参数的作用是在程序发生内存溢出 OutOfMemory 时打印日志,dump下来,方便用工…...

C语言代码 计算1!+2!+3!+4!+5!+6!+7!+8!+9!+10!
计算1!2!3!4!5!6!7!8!9!10! 代码示例: #include <stdio.h> int main() {int i 0;int n 0;int ret 1;int sum 0;for (n 1; n < 10; n){ret 1;for (i 1; i < n; i){ret ret * i;}sum sum ret;}printf("%d\n", sum);return 0; } 运…...
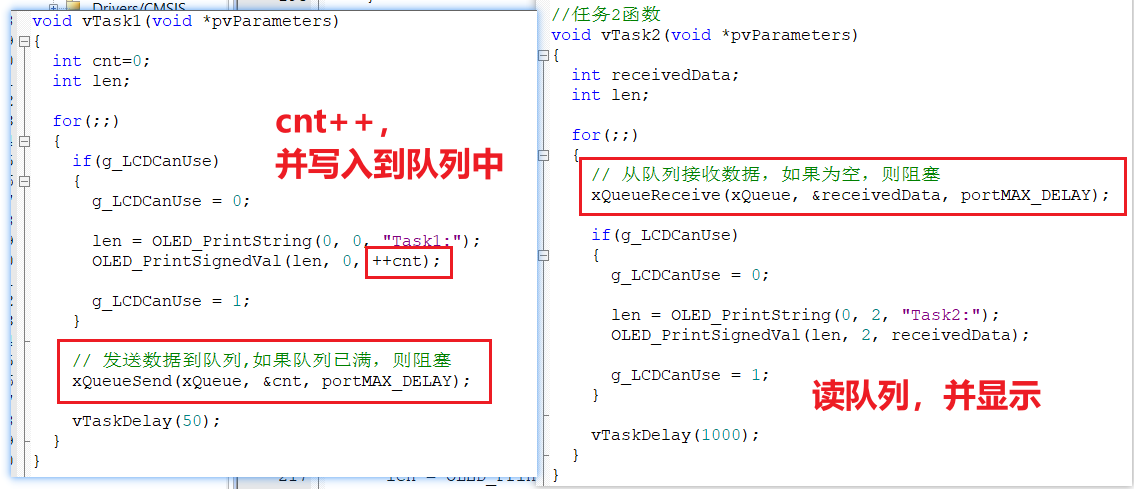
【RTOS】快速体验FreeRTOS所有常用API(4)队列
目录 四、队列2.1 概念2.2 创建队列2.3 写队列2.4 读队列2.5 队列集(可跳过) 四、队列 该部分在上份代码基础上修改得来,代码下载链接: https://wwzr.lanzout.com/iBNAS1l75bvc 密码:7xy2 该代码尽量做到最简,不添加多…...

【开题报告】基于SpringBoot的美食制作学习网站的设计设计与实现
1.选题背景 随着人们生活水平的提高,对美食的追求也越来越高。越来越多的人希望能够在家里制作出各种美味的菜肴。然而,对于许多人来说,缺乏专业的指导和实践经验是一个挑战。另外,互联网的普及与发展,为人们提供了更…...

Rosalind Java|Speeding Up Motif Finding
Rosalind编程问题之计算错误矩阵(failure array)输出前后缀检索匹配。 Speeding Up Motif Finding Problem: A prefix of a length n string s is a substring s[1:j]; a suffix of s is a substring s[k:n]. The failure array of s is a…...

打印的前后顺序
面试题经常会有 <script>console.log(1)setTimeout(function(){console.log(2)})console.log(3)let pnew Promise((resolve,reject) >{console.log(4)resloved(hhhhhh)})p.then(res >{console.log(res)console.log(5)},res >{console.log(7)})console.log(6)&l…...

Android Retrofit使用详情
一、 Retrofit是什么 Retrofit是Android用来接口请求的网络框架,内部是基于OkHttp实现的,retrofit负责接口请求的封装,retrofit可以直接将接口数据解析为Bean类、List集合等,直接简化了中间繁琐的数据解析过程 二、 Retrofit的简单…...

安全加密算法
常用加密算法 对称加密 加密和解密用到的密钥是相同的,这种加密方式加密速度非常快,适合经常发送数据的场合。缺点是密钥的传输比较麻烦。常用对称加密算法如下: DES:密钥长度8个字节,安全性不足,已被证明…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...