【蓝桥备赛】数组分割——组合数学?
题目链接
数组分割
个人思路
两个数组都需要和为偶数,那么就去思考一个数组如何才能和是偶数呢??
数组里肯定要么是奇数要么是偶数,偶数无论有多少个,都不会改变一个数组的奇偶性。但是奇数个奇数的和还是奇数,偶数个奇数的和就会是偶数(这个应该就不用证明了吧)。
那么这个问题就被转换为,求数组中奇数的个数!
当我们遍历完数组后,获取到数组中奇数与偶数的个数。如果奇数的数量为奇数,那么我们无论怎么去分,都无法将奇数个奇数分成两边都是偶数个奇数(即奇数无法拆成两个偶数),这种情况下,答案的个数就为 0。
那么如果为偶数(n)个奇数,那么我只需要每次从奇数中选择0,2,4,… ,n个奇数作为其中一个集合的数,剩下的交给另外一个集合,这就是数学中的组合问题,用公式表示就是:
C n 0 + C n 2 + … + C n n = 2 n − 1 C_{n}^{0}+C_{n}^{2}+\ldots +C_{n}^{n}=2^{n-1} Cn0+Cn2+…+Cnn=2n−1
对于偶数的话,我们就没有那么多限制,直接从中选取0,1,2,3,… ,n个偶数,随意组合:公式就是
C n 0 + C n 1 + C n 2 + … + C n n = 2 n C _{n}^{0}+C_{n}^{1}+C_{n}^{2}+\ldots +C_{n}^{n}=2^{n} Cn0+Cn1+Cn2+…+Cnn=2n
不过这边存在一个问题,如果奇数的个数为0个,那么就不存在 n-1的情况,所以需要特别处理。
另外在计算这些的过程中,可能会出现数过大的情况需要取模运算,我直接选择了快速幂。
参考代码
Java
import java.util.Scanner;public class Main {static int n;static long[] arr;static long res;static long MOD = 1000000007;static long ksm(long a, long b) {long cnt = 1;while (b > 0) {if ((b & 1) == 1) {cnt = cnt * a % MOD;}a = a * a % MOD;b >>= 1;}return cnt;}public static void main(String[] args) {Scanner sc = new Scanner(System.in);int t = sc.nextInt();while (t-- > 0) {n = sc.nextInt();arr = new long[n + 1];// odd 奇数个数int odd = 0;for(int i = 1; i <= n; ++i) {arr[i] = sc.nextLong();if(arr[i] % 2 == 1) {++odd;}}// 一个数组的和是否是偶数,取决于奇数的个数一定要是偶数个,剩余偶数的组合随意int even = n - odd;// 如果奇数的个数为奇数个,那么就无法组成和为偶数的数组if (odd % 2 == 1) {System.out.println(0);continue;}// 对于每一个奇数情况,都相当于从odd个中选i个(组合公式),但是i必须是偶数个// 选择完奇数后,剩余偶数从选0个到全选// 也就是在求 2^(odd - 1) * 2^even// 啊!!!震惊// 不过如果奇数为 0 个,此处就不用减去1了if(odd == 0) {res = ksm(2, even);} else {res = ksm(2, even) * ksm(2, odd - 1) % MOD;}System.out.println(res);}}
}
C++
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e3 + 3;
const ll MOD = 1000000007;int n;
ll arr[N];
ll res;ll ksm(ll a, ll b) {ll cnt = 1;while (b > 0) {if (b & 1) {cnt = (cnt * a) % MOD;}a = (a * a) % MOD;b >>= 1;}return cnt;
}int main() {int t;cin >> t;while (t-- > 0) {cin >> n;int odd = 0;for (int i = 1; i <= n; ++i) {cin >> arr[i];if (arr[i] % 2 == 1) {++odd;}}int even = n - odd;if (odd % 2 == 1) {cout << 0 << endl;continue;}if (odd == 0) {res = ksm(2, even);} else {res = (ksm(2, even) * ksm(2, odd - 1)) % MOD;}cout << res << "\n";}return 0;
}相关文章:

【蓝桥备赛】数组分割——组合数学?
题目链接 数组分割 个人思路 两个数组都需要和为偶数,那么就去思考一个数组如何才能和是偶数呢?? 数组里肯定要么是奇数要么是偶数,偶数无论有多少个,都不会改变一个数组的奇偶性。但是奇数个奇数的和还是奇数&…...

iphone5s基带部分电源部分主主电源供电及
时序: 1.,基带电源的供电,基带电源也叫pmu。 首先时序图说电池提供供电,电池是J6接口,视频习惯把接口称之为座子。查U2_RF芯片,发现供电信号为PP_BATT_VCC_CONN,但是没查到跟电池座子有关系,电池座子写的是…...
【每日一题】按分隔符拆分字符串
文章目录 Tag题目来源解题思路方法一:遍历方法二:getline 写在最后 Tag 【遍历】【getline】【字符串】【2024-01-20】 题目来源 2788. 按分隔符拆分字符串 解题思路 方法一:遍历 思路 分隔符在字符串开始和结束位置时不需要处理。 分隔…...
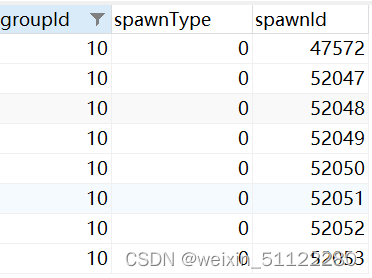
spawn_group_template | spawn_group | linked_respawn
字段介绍 spawn_group | spawn_group_template 用来记录与脚本事件或boss战斗有关的 creatures | gameobjects 的刷新数据linked_respawn 用来将 creatures | gameobjects 和 boss 联系起来,这样如果你杀死boss, creatures | gameobjects 在副本重置之前…...
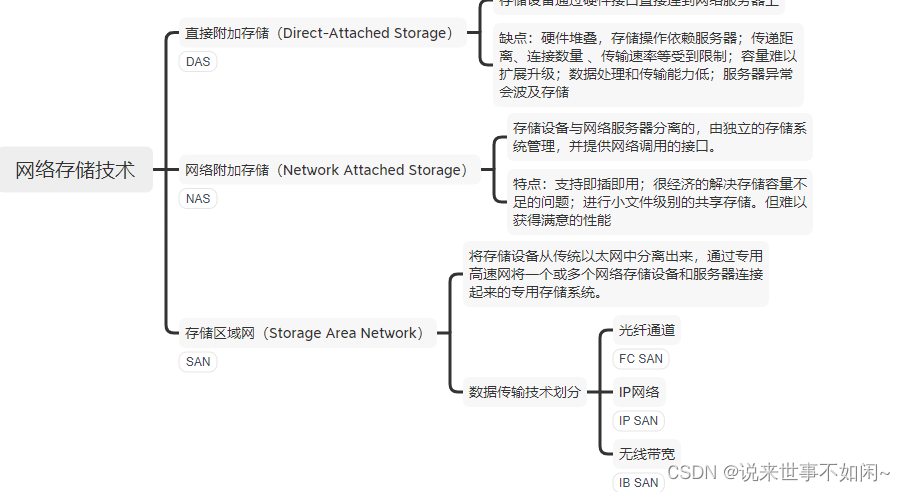
软考系分之计算机网络规划设计、综合布线、RAID和网络存储等
文章目录 1、概要2、网络的三层模型3、综合布线系统4、廉价磁盘冗余阵列(RAID)5、网络存储6、总结 1、概要 本篇重点介绍计算机网络中的网络规划设计、综合布线、RAID和网络存储。 2、网络的三层模型 三层模型分为核心层、汇聚层和接入层,接…...
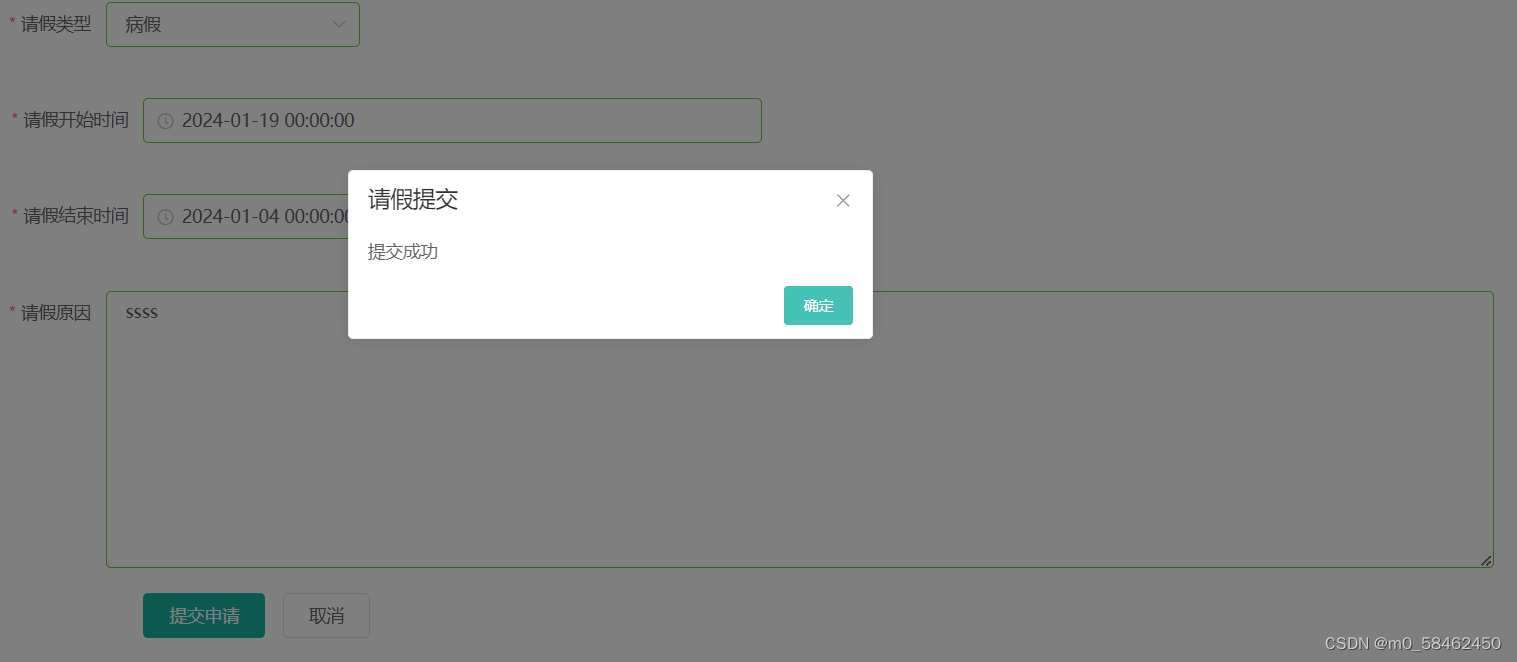
使用ElEment组件实现vue表单校验空值
1.绑定表单组件数组rules 2.在data域中设定组件rules 3.设定调用方法函数 提交校验 取消: 测试页面 提交空值 失去焦点 取消重置 提交后重置...

processing集训day01
介绍 Processing是一门开源编程语言,提供了对图片,动画和声音进行编程的环境。学生,艺术家,设计师,建筑师,研究人员和业余爱好者可以使用Processing进行学习,制作原型以及作为生产工具。你可以…...
java面试——juc篇
目录 一、线程基础 1、进程与线程的区别?(⭐⭐⭐) 2、并行和并发的区别(⭐) 3、创建线程的方式有哪些?(⭐⭐⭐⭐) runnable和Callable的区别: 线程中的run()和 star…...

CSS 实现卡片以及鼠标移入特效
CSS 实现卡片以及鼠标移入特效 文章目录 CSS 实现卡片以及鼠标移入特效0、效果预览默认鼠标移入后 1、创建卡片组件2、添加样式3、完整代码 0、效果预览 默认 鼠标移入后 在本篇博客中,我们将探讨如何使用 CSS 来实现卡片组件,并添加鼠标移入特效&#…...

芯课堂 | SWM34S系列驱动TFT-LCD显示模组应用基本注意事项
1、确认硬件的连接、包括电源、地、RGB 数据线、DCLK\DE\HSYNC\VSYNC 等,显示模组有 DISP、RESET、CS、SCL、SDA 等。 2、确认各电压的正常,包括电源,部分有 IOVCC、VGL、VGH、VCOM 等电压 3、如果应用的 TFT-LCD 模组非演示例程中已适配调…...
java8 列表通过 stream流 根据对象属性去重的三种实现方法
java8 列表通过 stream流 根据对象属性去重的三种实现方法 一、简单去重 public class DistinctTest {/*** 没有重写 equals 方法*/SetterGetterToStringAllArgsConstructorNoArgsConstructorpublic static class User {private String name;private Integer age;}/*** lombo…...
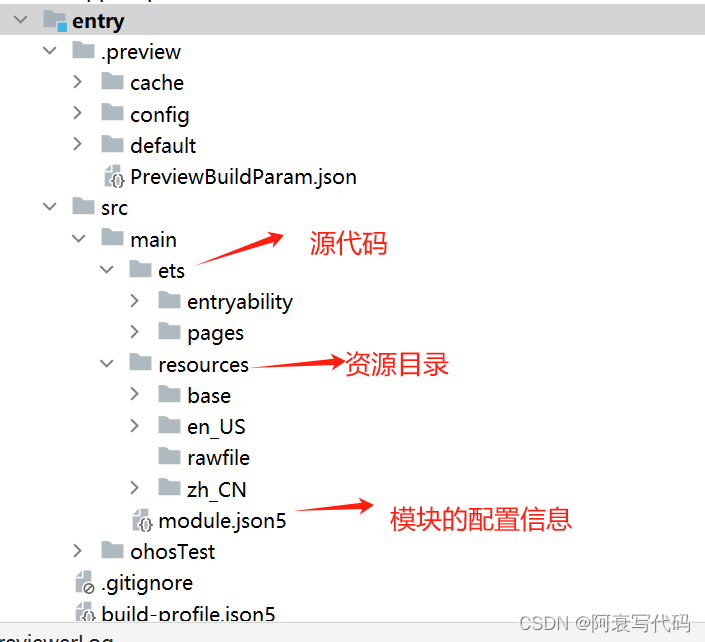
鸿蒙开发DevEco Studio Setup 工具认识及使用
1、界面认识 1.1 创建页面之前理解Ability 1.2 理解stage模式 1.3 工程级别目录结构 1.4 模块级别目录...

程序员裁员潮:技术变革下的职业危机
程序员裁员潮:技术变革下的职业危机 一对来自中国的工程师夫妻在美身亡,疑因谷歌裁员致悲剧发生。在技术变革下,裁员对于程序员的影响到底有多大?快来和我们分享一下你的看法吧~ 哎,这是悲哀,让我又想起来…...
Cesium快速入门
文章目录 0.引言1.Cesium环境搭建1.1安装Node.js环境1.2配置Cesium依赖 2.搭建第一个Cesium程序2.1引入源码编译结果2.2创建html文件2.3编写第一个Cesium程序2.4申请许可密钥2.5发布Cesium程序服务 3.界面介绍4.默认控件介绍 0.引言 现有的gis开发方向较流行的是webgis开发&am…...

Android.mk和Android.bp的区别和转换详解
Android.mk和Android.bp的区别和转换详解 文章目录 Android.mk和Android.bp的区别和转换详解一、前言二、Android.mk和Android.bp的联系三、Android.mk和Android.bp的区别1、语法:2、灵活性:3、版本兼容性:4、向后兼容性:5、编译区…...

卡尔曼滤波器原理By_DR_CAN 学习笔记
DR_CAN卡尔曼滤波器 Kalman Filter Recursive Algorithm迭代过程 数学基础正态分布和6-SigmaData FusionCovariance MatrixState Space Representation离散化推导 linearizationTaylor Series2-DSummary Step by Step Derivation of Kalman Gain矩阵求导公式 Prior / Posterio…...

013 异常
文章目录 异常人为创造异常 异常 定义:运行时检测的错误 try:可能触发异常的语句 except 错误类型1 [as 变量1]:处理语句1 except 错误类型2:处理语句2 except Exception:不是以上错误类型的处理语句 else:未发生异常的语句 finally:无论是否发生异常的语句异常处理:保障程序…...
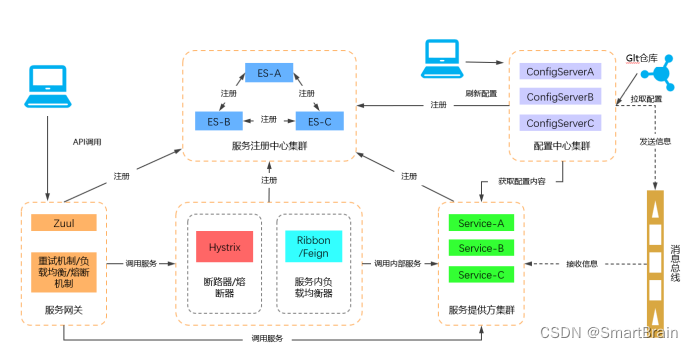
微服务Spring Cloud架构详解
"Spring Cloud为开发人员提供了快速构建分布式系统中一些常见模式的工具(例如配置管理,服务发现,断路器,智能路由,微代理,控制总线)。分布式系统的协调导致了样板模式, 使用Spring Cloud开…...

推荐一一款小众黑科技工具,低调使用建议收藏
wireshark是个啥就不多说了,非常流行的网络封包分析软件。 可以截取各种网络封包,显示网络封包的详细信息。 软件功能十分强大,操作也不复杂。 很多小友都在后台问能不能出一期完整的抓包分析贴,今天给你们安排上了哈。 01 W…...

HiP框架:多AI模型联手,助力机器人驾驭复杂规划大局
原创 | 文 BFT机器人 你的日常待办清单或许只是些稀松平常的小事:清洗堆积如山的碗盘、采购琳琅满目的食品杂货等。在执行这些任务时,你无需逐一写下“捧起那只满是油污的盘子”或“用湿润的海绵仔细擦洗这个盘子”这样的琐碎步骤,因为在你的…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...
