【数据结构和算法】--- 二叉树(3)--二叉树链式结构的实现(1)
目录
- 一、二叉树的创建(伪)
- 二、二叉树的遍历
- 2.1 前序遍历
- 2.2 中序遍历
- 2.3 后序遍历
- 三、二叉树节点个数及高度
- 3.1 二叉树节点个数
- 3.2 二叉树叶子节点个数
- 3.3二叉树第k层节点个数
- 3.4 二叉树查找值为x的节点
- 四、二叉树的创建(真)
一、二叉树的创建(伪)
在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入,且为了方便后面的介绍,此处手动快速创建一棵简单的二叉树,快速进入二叉树操作学习,等二叉树结构了解的差不多时,我们反过头再来研究二叉树真正的创建方式。
基于二叉树的链式结构,于是可以先malloc动态开辟出二叉树的每个节点并初始化,然后通过节点中的指针struct BinaryTreeNode* left(指向左树)和struct BinaryTreeNode* right(指向右树),将各个节点连接起来,最后大致模拟出了一棵二叉树,代码如下:
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left; //左树struct BinaryTreeNode* right; //右树
}BTNode;
BTNode* CreatBinaryTree()
{//动态开辟节点BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);//链接节点node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}
在实现二叉树基本操作前,再回顾下二叉树的概念,一棵二叉树是结点的一个有限集合,该集合:
- 或者为空
- 由一个根节点加上两棵分别称为左子树和右子树的二叉树组成
二叉树满足的条件:
- 二叉树不存在度大于2的结点;
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树。
其余二叉树的概念还请回顾:【数据结构和算法】—二叉树(1)–树概念及结构
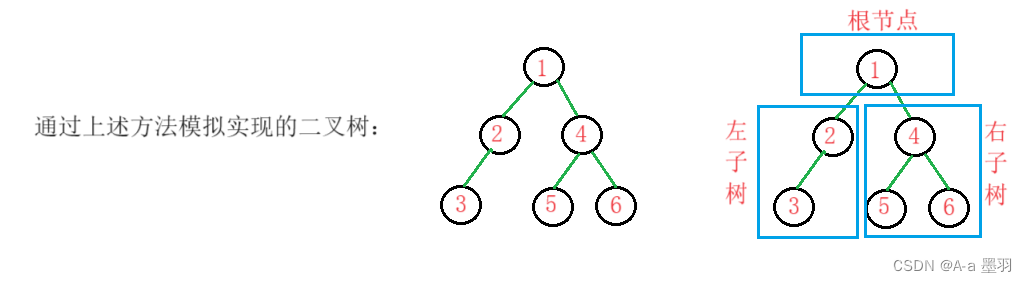
从概念中可以看出,二叉树定义是递归式的,因此后序基本操作中基本都是按照该概念实现的。
注意: 上述代码并不是创建二叉树的方式,真正创建二叉树方式将在后面介绍。
二、二叉树的遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。 访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。下图可以理解为是二叉树的前序遍历:

按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:
- 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
- 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。
- 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树和根的右子树。 NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
2.1 前序遍历
前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。 依据此规律我们便可如下遍历二叉树,为了方便观察,每次遍历到根节点都输出一下:
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){putchar('N');return;}putchar(root->val); //访问根节点BinaryTreePrevOrder(root->left); //访问左子树BinaryTreePrevOrder(root->right); //访问右子树
}
前序遍历代码,逻辑结构大致如下图,可以参考一下:
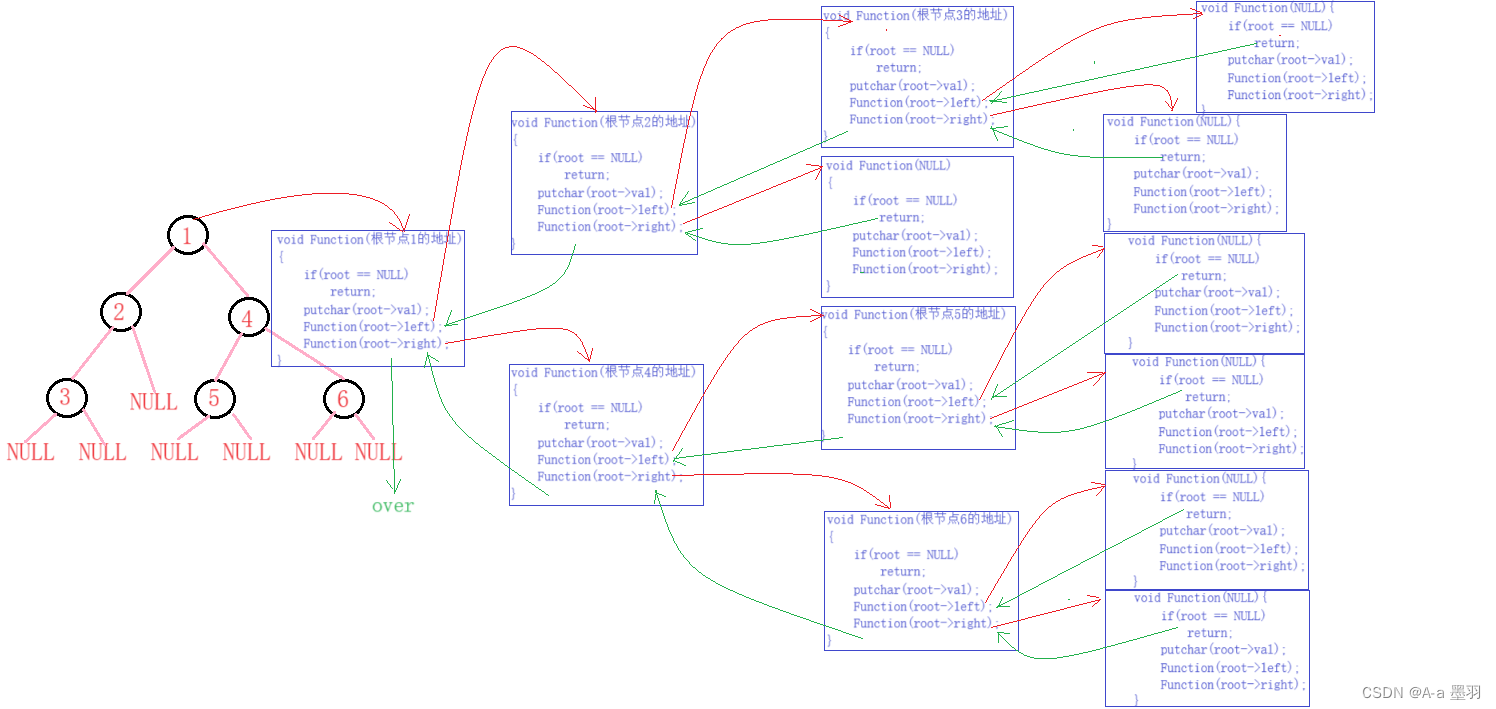
在这利用递归思想来解决前序遍历的问题,因为是前序遍历(访问顺序依次是根节点,左子树,右子树),所以在进入下层递归前可以先输出根节点。当进入左/右子树时,会更新根节点(原为上层根节点的左/右孩子节点) 。二叉树的叶子节点的左右孩子都为NULL,那么便可将递归的结束条件定为NULL。这便是前序遍历的递归逻辑。
2.2 中序遍历
中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。 与前序遍历相似,只是访问顺序不同(依次是左子树,根节点,右子树),那么调整一下代码顺序即可,将输出根节点值的操作(putchar(root->val);),放在访问左子树之后。那么递归每次都会先进入左子树,且最先打印的为叶子节点。代码如下:
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{if (root == NULL){putchar('N');return;}BinaryTreeInOrder(root->left); //访问左子树putchar(root->val); //输出根节点BinaryTreeInOrder(root->right); //访问右子树
}
2.3 后序遍历
后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。 同样与前序遍历相似,访问顺序不同(依次是左子树,右子树,根节点),依此特性所以我们只需将输出操作(putchar(root->val))放到最后,其余代码不变。实现思想-递归完左子树和右子树后再输出根节点。 代码如下:
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{if (root == NULL){putchar('N');return;}BinaryTreePostOrder(root->left); //访问左子树BinaryTreePostOrder(root->right); //访问右子树putchar(root->val); //输出根节点
}
三种遍历最后输出的结果(图中N表示递归时遇到了NULL):
- 前序遍历结果:1 2 3 4 5 6
- 中序遍历结果:3 2 1 5 4 6
- 后序遍历结果:3 2 5 6 4 1

- 设一课二叉树的中序遍历序列:badce,后序遍历序列:bdeca,则二叉树前序遍历序列为 ( D )。
A adbce
B decab
C debac
D abcde解: 解题思想(给定两种遍历序列,求出另外一种):我们可以根据各种遍历方法的特性来求解。( 1 ) 根据后续遍历序列找出根节点,因为后续遍历最后才会输出根,那么在序列的最后一个即为根节点
a;( 2 ) 接着在中序遍历序列中找出根节点,然后划分左子树和右子树;( 3 ) 然后再到后序遍历序列中去除左子树和根节点,那么得到的便是右子树,并将其看为独立的树;( 4 ) 重复上述三步操作,直到排出完整的树。
图解如下:
解决此类问题最重要的还是要弄懂代码的递归思想。
三、二叉树节点个数及高度
3.1 二叉树节点个数
求二叉树的节点个数,利用的还是递归思想。我们可以将问题转化为----根节点(1),左子树的节点个数(root->left)和右子树的节点个数(root->right)的总结点个数。我们可以将根节点为空(root == NULL)作为递归结束的条件,并返回0(return 0)。 这种方法通常被称为递归分治。
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{if (root == NULL)return 0;return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
代码图解:
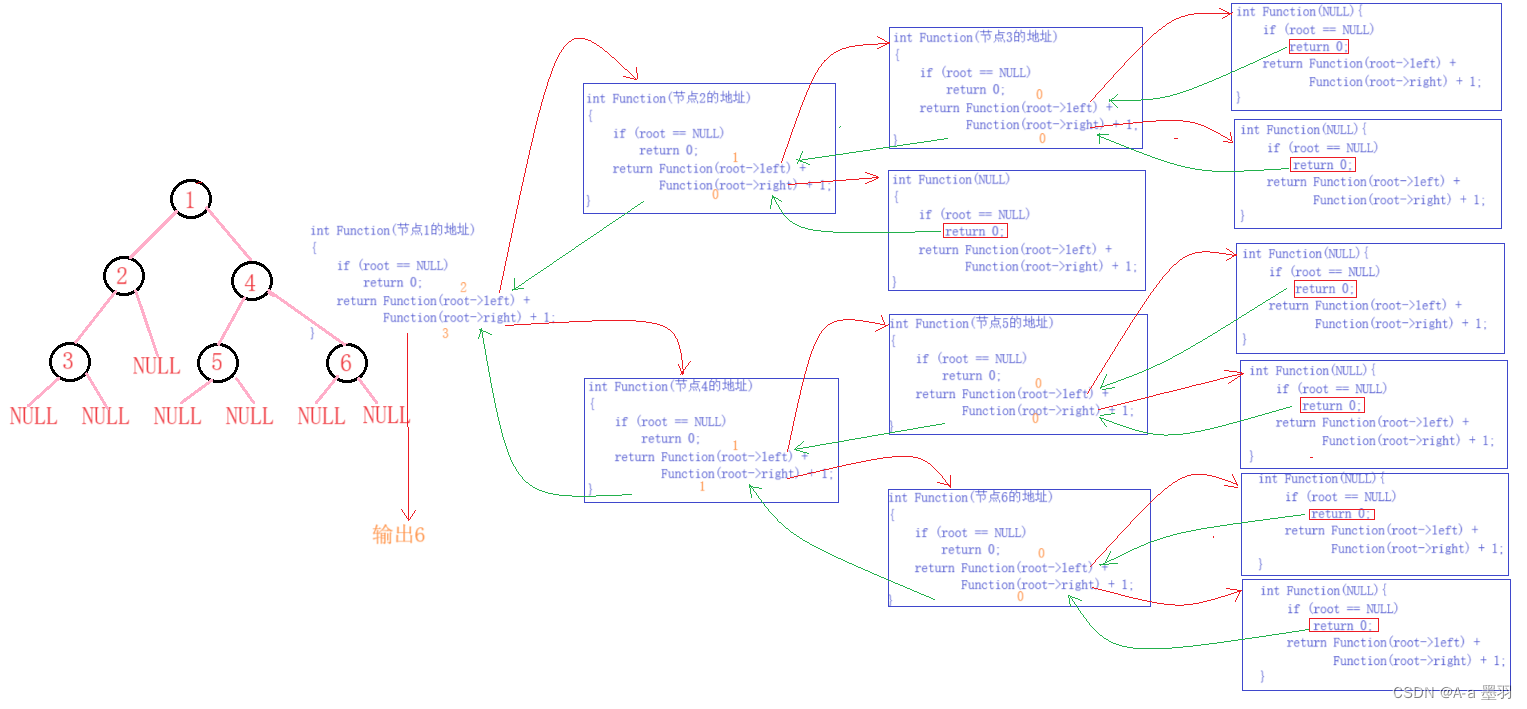
3.2 二叉树叶子节点个数
叶子节点概念:含有的子树个数为0的节点。 如本次创建的二叉树的节点3,节点5,节点6。
基于叶子节点的特性,同样可以利用递归分治的方法,将问题同化为----左子树的叶子节点个数和右子树的叶子节点个数之和。
函数返回的条件:
- 当前节点(
root)的左子树(root->left)和右子树(root->right)都为空时(即!(root->left && root->right)),那么此节点为叶子节点,并返回1; - 当前节点为空节点(即
(root == NULL)),返回0; - 函数执行到最后,返回当前树的叶子节点数。
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (!(root->left && root->right))return 1;return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
代码图解:
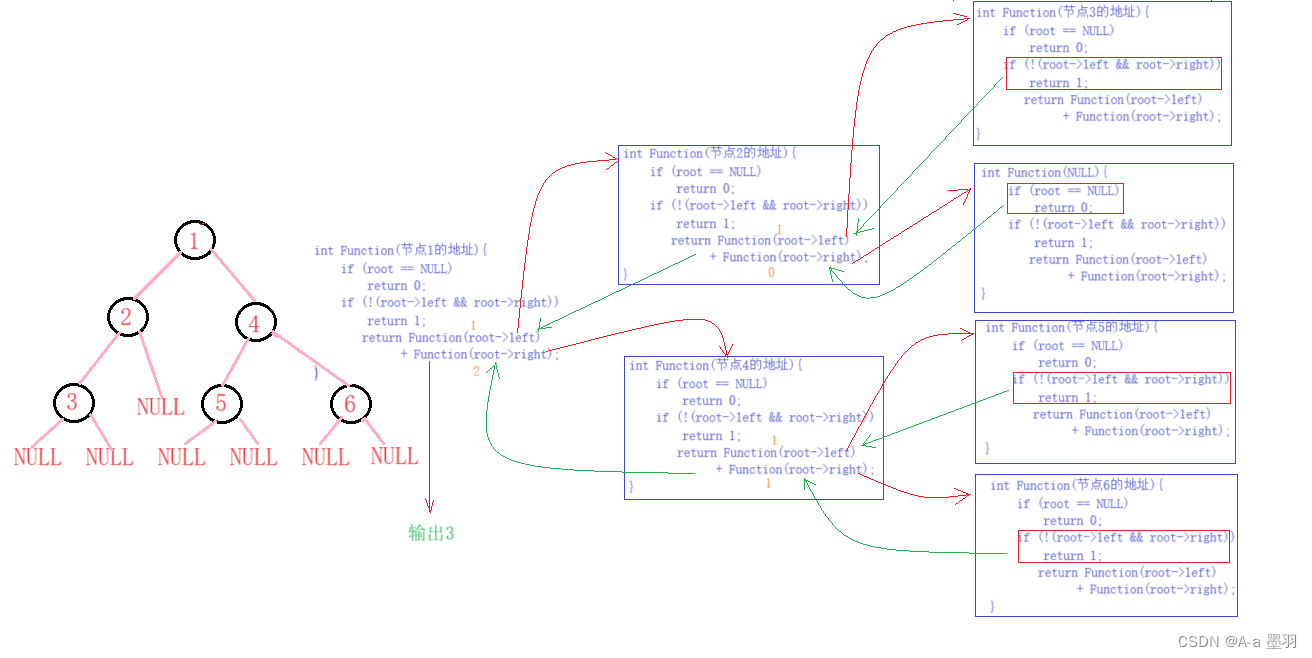
3.3二叉树第k层节点个数
既然是求第k层的节点个数,那我们便可以定义一个变量k,记录当前函数所要递归的层数。既然k的值是变化的,那么可以将他作为函数的参数,每递归一层便让他减一k - 1,那么当k的值到1时,便是我们所要求的二叉树的第k层。
依据上述关系,便可以得出 函数返回的条件:
- 当遇到空节点时(
root == NULL),返回0; - 当
k == 1时(说明到了二叉树的第k层),且当前节点不为空(root != NULL),那么便可返回1; - 函数执行到了最后,返回统计到的符合条件的节点个数。
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL)return 0;if (k == 1 && root != NULL)return 1;return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}
根据函数返回条件不难发现,当k == 1时递归便不会继续往下层执行,这是因为此时函数必定会满足两个if条件中的一个,这也避免了递归到二叉树的第k + 1层。
代码图解:
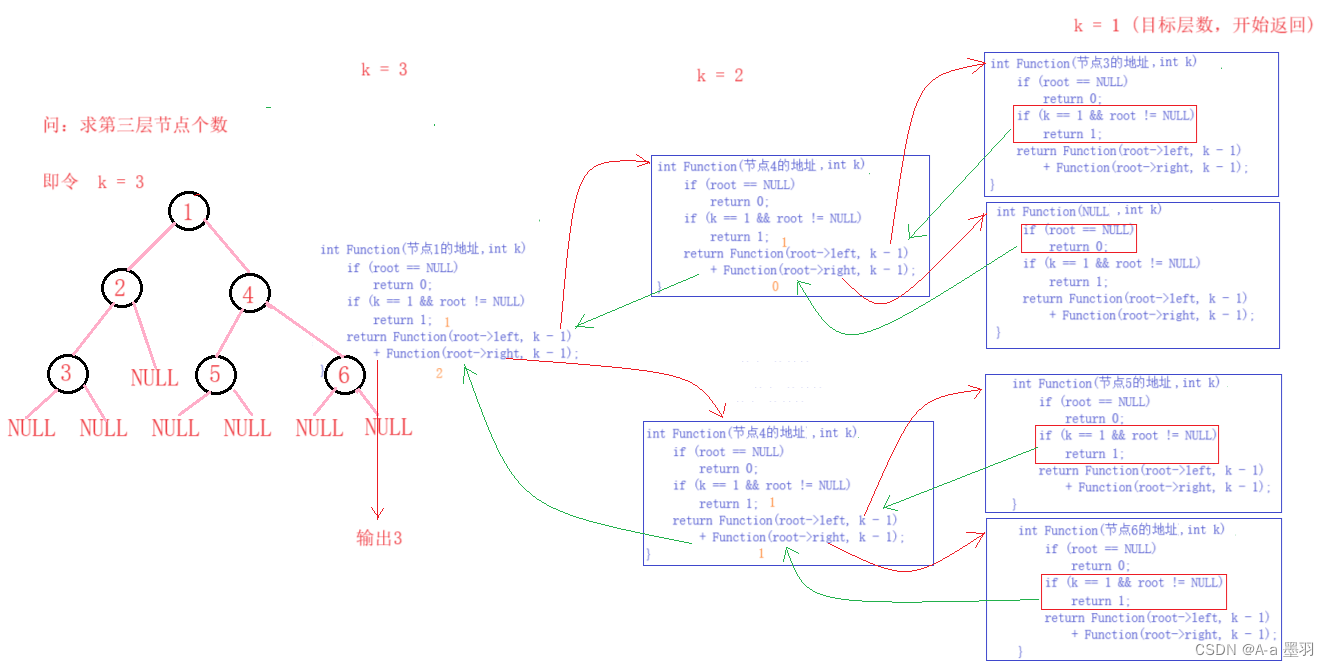
3.4 二叉树查找值为x的节点
查找值为x的节点,可以将递归分治为----判断当前节点,判断左子树,判断右子树。 那么当遇到空节点(root == NULL)就返回return NULL;如果遇到所要查找的值(root->val == x)就返回当前地址(return root);那么如果都不满足就继续搜寻左子树,然后右子树;直到最后搜寻完整棵二叉树,都没有找到x,那么便返回NULL。
还需要注意的一个问题是,如果在递归过程中找到了目标值x,返回了当前地址root,但是现在只是回到了上一层递归的地方,返回值并不会被接收,而是继续执行下一个逻辑。 那么我们便可以用BTNode* ret1来接受函数的返回值,并判断,当返回值(ret1)不为NULL时(即说明上一次递归时,找到了x)直接返回此值return ret1。
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{//空节点if (root == NULL)return NULL;//值为x的节点if (root->val == x)return root;//左子树递归,ret接收返回值,并判断BTNode* ret1 = BinaryTreeFind(root->left, x);if (ret1 != NULL)return ret1;//方法一:易于理解//BTNode* ret2 = BinaryTreeFind(root->right, x);//if (ret2 != NULL)// return ret2;return BinaryTreeFind(root->right, x);return NULL;
}
代码图解:
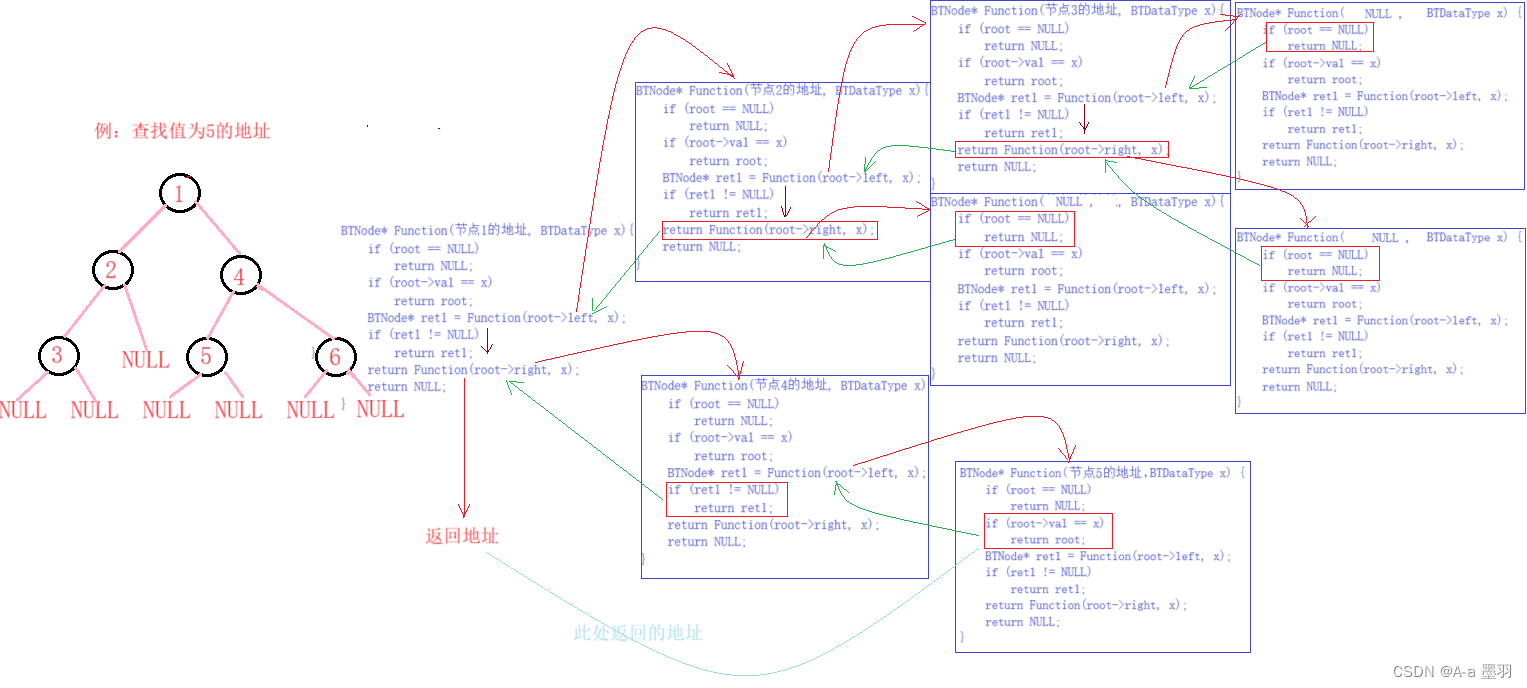
四、二叉树的创建(真)
通过上面对各种遍历方法和递归思想的讲解,相信使用递归来真正创建二叉树也不难了,如下:
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int* pi)
{//判断是否为空,即当a[*pi] == '#'时if (a[*pi] == '#'){(*pi)++;return NULL;}//动态开辟节点BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc()::fail");exit(-1);}//赋值并连接(递归)node->val = a[*pi];(*pi)++;node->left = BinaryTreeCreate(a, pi);node->right = BinaryTreeCreate(a, pi);retur
上面介绍的二叉树的一些函数的执行结果如下:
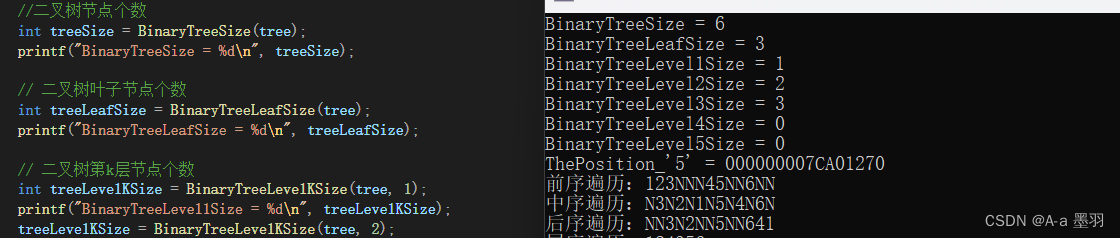
另外还有一些较为复杂的函数将在下一篇文章中介绍。
相关文章:

【数据结构和算法】--- 二叉树(3)--二叉树链式结构的实现(1)
目录 一、二叉树的创建(伪)二、二叉树的遍历2.1 前序遍历2.2 中序遍历2.3 后序遍历 三、二叉树节点个数及高度3.1 二叉树节点个数3.2 二叉树叶子节点个数3.3二叉树第k层节点个数3.4 二叉树查找值为x的节点 四、二叉树的创建(真) 一、二叉树的创建(伪) 在学习二叉树的基本操作前…...

Cesium for Unity包无法加载
太上老君急急如律⚡令⚡ 🥙关闭UnityHub🧀启动梯子🥪cmd 启动UnityHub 🥙关闭UnityHub 🧀启动梯子 🥪cmd 启动UnityHub 把批处理启动文件👈中的exe的路径换成自己的安装目录!保存…...

Leetcode—40.组合总和II【中等】
2023每日刷题(七十七) Leetcode—40.组合总和II 算法思想 实现代码 class Solution { public:vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {vector<vector<int>> ans;vector<int…...

vscode连不上虚拟机,一直密码错误
最近在做毕设,但是vscode使用连接不上虚拟机,我以为是网络配置的问题,一顿查阅没找到原因。 后来查了一下ssh的日志,发现ssh有消息,但是也提示密码错误。 没找到密码配置格式什么的,经查看sshd配置文件发现…...

力扣每日一题 --- 972. 相等的有理数
本题中的一个难点是怎么判断是否相等,如果自己写判断的话是不是很麻烦,判断整数之后再去判断小数部分,那么我们这题的另一个难点就要登场了,第一个难点让本题的情况变得复杂,第二个难点让本题变得很难想到怎么判断&…...

EXECL 单元格字符串链接 CONCAT :应用:将一行数据转为json
源: 目标 函数表示 CONCAT("data", CHAR(10), "{", CHAR(10), " ", "ulAlarmId : ", A5, CHAR(10), " ", "ulAlarmLevel : ", D5, CHAR(10)," ", "bBo…...

基于Python实现人脸识别相似度对比
目录 引言背景介绍目的和意义 人脸识别的原理人脸图像获取人脸检测与定位人脸特征提取相似度计算 基于Python的人脸相似度对比实现数据集准备人脸图像预处理特征提取相似度计算 引言 背景介绍 人脸识别技术是一种通过计算机对人脸图像进行分析和处理,从而实现自动识…...

CSS 蜡烛效果
<template><view class="holder"><!-- 身子 --><view class="candle"><!-- 光源 --><view class="blinking-glow"></view><!-- 火星子 --><view class="thread"></view>…...

渗透测试之Kali如何利用CVE-2019-0708漏洞渗透Win7
环境: 1.攻击者IP:192.168.1.10 系统: KALI2022(vmware 16.0) 2.靶机IP:192.168.1.8 系统:Windows 7 6.1.7601 Service Pack 1 Build 7601 已开启远程协助RDP服务开启了3389端口 问题描述: KALI 如何利用CVE-2019-0708漏洞渗透Win7 解决方案: 1.打开kali,msf搜索…...

Docker(二)安装指南:主要介绍在 Linux 、Windows 10 和 macOS 上的安装
作者主页: 正函数的个人主页 文章收录专栏: Docker 欢迎大家点赞 👍 收藏 ⭐ 加关注哦! 安装 Docker Docker 分为 stable test 和 nightly 三个更新频道。 官方网站上有各种环境下的 安装指南,这里主要介绍 Docker 在…...

LeetCode 410. 分割数组的最大值
一、题目 1、题目描述 给定一个非负整数数组 nums 和一个整数 k ,你需要将这个数组分成 k 个非空的连续子数组。 设计一个算法使得这 k 个子数组各自和的最大值最小。 2、接口描述 class Solution { public:int splitArray(vector<int>& nums, int …...

linux shell脚本 基础认识
Linux 系统中的 Shell 是一个特殊的应用程序,它介于操作系统内核与用户之间,充当 了一个“命令解释器”的角色,负责接收用户输入的操作指令(命令)并进行解释,将需要执行的操作传递给内核执行,并…...

一文(10图)了解Cornerstone3D核心概念(万字总结附导图)
Cornerstone3D介绍 Cornerstone3D是一个专门为处理三维医学影像而设计的JavaScript库。 它是Cornerstone项目的一部分,旨在为医学影像社区提供高性能、可扩展且易于使用的开源Web工具,专注于提供交互式的3D医学图像浏览体验,适用于多种医学…...
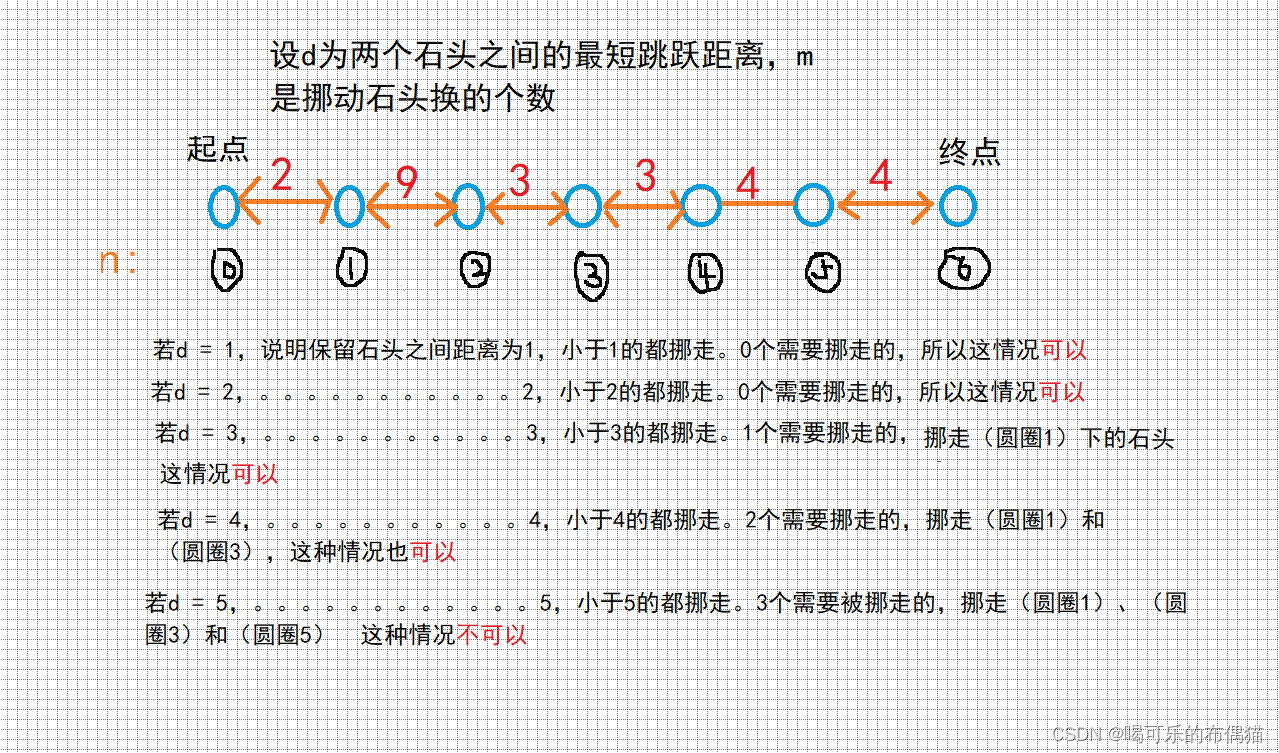
牛客网-----跳石头
题目描述: 一年一度的“跳石头”比赛又要开始了! 这项比赛将在一条笔直的河道中进行,河道中分布着一些巨大岩石。组委会已经选择好了两块岩石作为比赛起点和终点。在起点和终点之间,有N块岩石(不含起点和终点的岩石)。在比赛过程中࿰…...

用ChatGPT教学、科研!大学与OpenAI合作
亚利桑那州立大学(简称“ASU”)在官网宣布与OpenAI达成技术合作。从2024年2月份开始,为所有学生提供ChatGPT企业版访问权限,主要用于学习、课程作业和学术研究等。 为了帮助学生更好地学习ChatGPT和大语言模型产品,AS…...
运维平台介绍:视频智能运维平台的视频质量诊断分析和告警中心
目 录 一、视频智能运维平台介绍 (一)平台概述 (二)结构图 (三)功能介绍 1、运维监控 2、视频诊断 3、巡检管理 4、告警管理 5、资产管理 6、工单管理 7、运维…...

GAMES104-现代游戏引擎:从入门到实践 - 物理引擎课程笔记汇总
文章目录 0 入门资料1 物理引擎基本概念Actor & shapesRigid body dynamicsCollision DetectionCollision Resolution 应用与实践Character controllerRagdoll 0 入门资料 GAMES104-现代游戏引擎:从入门到实践_课程视频_bilibiliGAMES104官方账号 - 知乎课程主页…...

【linux】Xorg的工作原理
介绍 在linux系统上执行nvidia-smi时,总有一个进程占用gpu。 1 N/A N/A 2174 G /usr/lib/xorg/Xorg 4MiB /usr/lib/xorg/Xorg 是与X Window System(简称X11或X)相关的一个应用程序。X Window System是一个…...

02-docker下部署seata
官方部署文档 http://seata.io/zh-cn/docs/ops/deploy-by-docker 配置参数说明 http://seata.io/zh-cn/docs/user/configurations 1、镜像拉取 docker pull seata-server2、复制配置文件 mkdir /home/server/seata cd /home/server/seata docker run -d -p 8091:8091 -p 709…...
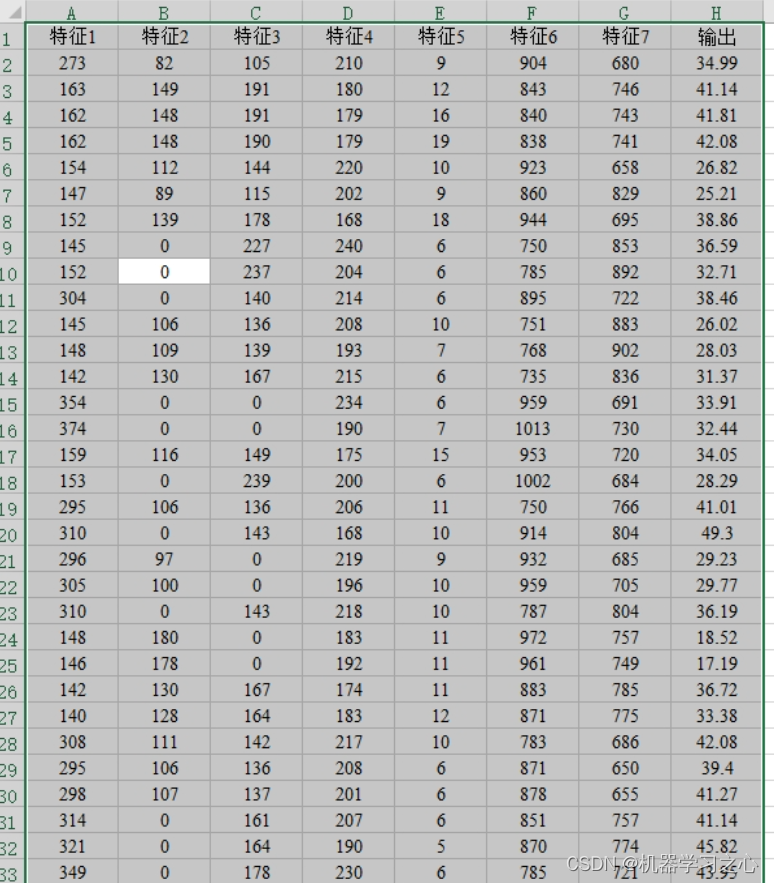
回归预测 | Matlab实现GA-APSO-MBP、GA-MBP、MBP、BP多输入单输出回归预测
回归预测 | Matlab实现GA-APSO-MBP、GA-MBP、MBP、BP多输入单输出回归预测 目录 回归预测 | Matlab实现GA-APSO-MBP、GA-MBP、MBP、BP多输入单输出回归预测预测效果基本描述程序设计参考资料 预测效果 基本描述 1.Matlab实现GA-APSO-MBP、GA-MBP、MBP、BP多输入单输出回归预测&…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...