C++面试:stl的栈和队列介绍
目录
栈
栈(stack)的声明:
push(): 将元素推入栈顶
pop(): 弹出栈顶元素
top(): 访问栈顶元素,但不弹出
empty(): 检查栈是否为空
size(): 返回栈中元素的数量
emplace(): 在栈顶构造一个元素
== 和 !=: 用于比较两个栈是否相等或不相等
队列
队列(queue)的声明:
push(): 将元素推入队列尾部
pop(): 从队列头部弹出元素
front(): 访问队列头部元素
back(): 访问队列尾部元素
empty(): 检查队列是否为空
总结
栈
栈(stack)的声明:
#include <stack>// 声明一个整数类型的栈
std::stack<int> myStack;// 在栈中压入元素
myStack.push(10);
myStack.push(20);// 弹出栈顶元素
myStack.pop();// 访问栈顶元素
int topElement = myStack.top();
push(): 将元素推入栈顶
#include <stack>std::stack<int> myStack;myStack.push(10);
myStack.push(20);
pop(): 弹出栈顶元素
myStack.pop();
top(): 访问栈顶元素,但不弹出
int topElement = myStack.top();
empty(): 检查栈是否为空
if (myStack.empty()) {// 栈为空
}
size(): 返回栈中元素的数量
size_t stackSize = myStack.size();
emplace(): 在栈顶构造一个元素
myStack.emplace(30);
== 和 !=: 用于比较两个栈是否相等或不相等
std::stack<int> stackA;
std::stack<int> stackB;// ...if (stackA == stackB) {// 栈A和栈B相等
}if (stackA != stackB) {// 栈A和栈B不相等
}
妙用
逆波兰表达式计算: 使用栈来计算逆波兰表达式。运算符遇到时,弹出栈顶的操作数进行计算,并将结果重新压入栈。
// 逆波兰表达式:3 4 + 5 *
std::stack<int> st;
st.push(3);
st.push(4);
st.push(st.top() + 5); // 3 + 4
st.pop();
int result = st.top() * 5; // (3 + 4) * 5
括号匹配检查: 使用栈来检查表达式中的括号是否匹配。遍历表达式,遇到左括号压入栈,遇到右括号时检查栈顶是否是对应的左括号。
std::stack<char> st;
std::string expression = "((a + b) * (c - d))";
for (char c : expression) {if (c == '(') {st.push(c);} else if (c == ')') {if (st.empty() || st.top() != '(') {// 括号不匹配break;}st.pop();}
}
bool isBalanced = st.empty();
函数调用堆栈: 编程语言中的函数调用使用堆栈来保存局部变量和返回地址。当函数调用时,创建一个新的栈帧,函数执行完毕后,将栈帧弹出。
void func1() {int x = 10;// ...
}void func2() {int y = 20;// ...
}int main() {func1();func2();return 0;
}
队列
队列(queue)的声明:
#include <queue>// 声明一个整数类型的队列
std::queue<int> myQueue;// 在队列尾部插入元素
myQueue.push(30);
myQueue.push(40);// 从队列头部弹出元素
myQueue.pop();// 访问队列头部元素
int frontElement = myQueue.front();
push(): 将元素推入队列尾部
#include <queue>std::queue<int> myQueue;myQueue.push(10);
myQueue.push(20);
pop(): 从队列头部弹出元素
myQueue.pop();
front(): 访问队列头部元素
int frontElement = myQueue.front();
back(): 访问队列尾部元素
int backElement = myQueue.back();
empty(): 检查队列是否为空
if (myQueue.empty()) {// 队列为空
}
队列妙用
广度优先搜索(BFS): 在图或树的遍历中,使用队列来实现广度优先搜索,确保按照层次遍历节点。
void BFS(Node* root) {std::queue<Node*> q;q.push(root);while (!q.empty()) {Node* current = q.front();// 处理当前节点// ...// 将当前节点的邻居节点入队for (Node* neighbor : current->neighbors) {q.push(neighbor);}// 出队q.pop();}
}
任务调度: 在操作系统或并发编程中,使用队列来管理任务队列,确保按照先进先出的原则执行任务。
#include <queue>
#include <thread>
#include <iostream>std::queue<std::function<void()>> taskQueue;
std::mutex taskQueueMutex;void workerThread() {while (true) {std::function<void()> task;{std::lock_guard<std::mutex> lock(taskQueueMutex);if (!taskQueue.empty()) {task = taskQueue.front();taskQueue.pop();}}if (task) {task();} else {// Sleep or yield to avoid busy-waitingstd::this_thread::yield();}}
}
缓存管理: 使用队列来管理缓存中的数据,确保最先进入缓存的数据最先被替换。
#include <queue>
#include <iostream>std::queue<int> cache;void addToCache(int data) {cache.push(data);// 如果缓存大小超过限制,移除队首元素if (cache.size() > MAX_CACHE_SIZE) {cache.pop();}
}
打印任务队列: 模拟打印任务的队列,确保先提交的打印任务先得到执行。
#include <queue>
#include <iostream>std::queue<std::string> printQueue;void submitPrintJob(const std::string& document) {printQueue.push(document);
}void printNextJob() {if (!printQueue.empty()) {std::string document = printQueue.front();std::cout << "Printing: " << document << std::endl;printQueue.pop();}
}
总结
栈(Stack)和队列(Queue)是两种基本的数据结构,分别以后进先出(Last-In-First-Out,LIFO)和先进先出(First-In-First-Out,FIFO)的原则组织数据。在面试中,它们常被用于解决各种问题。
相关文章:

C++面试:stl的栈和队列介绍
目录 栈 栈(stack)的声明: push(): 将元素推入栈顶 pop(): 弹出栈顶元素 top(): 访问栈顶元素,但不弹出 empty(): 检查栈是否为空 size(): 返回栈中元素的数量 …...

从0开始学习C++ 第十二课:指针强化
第十二课:指针强化 学习目标: 理解常量指针与指针常量的区别。学习如何使用函数指针。掌握指针与数组的高级使用技巧。 学习内容: 常量指针与指针常量 概念: 常量指针是一个指向常量的指针,这意味着不能通过这个指针…...

mongodb和python交互
1. mongdb和python交互的模块 pymongo 提供了mongdb和python交互的所有方法 安装方式: pip install pymongo 2. 使用pymongo 2.1 导入pymongo并选择要操作的集合 数据库和集合能够自动创建 2.1.1 无需权限认证的方式创建连接对象以及集合操作对象 from pymongo import Mong…...

力扣279. 完全平方数
动态规划 思路: 假设 dp[i] 为最少组成数 i 的平方数个数;则其上一个状态为 dp[i - j^2] 1,1 为 j^2: 即 i 的最少完全平方数 i - j^2 的最少完全平方数 1,其中 j^2 < i 为最接近 i 的平方数;初始值…...

【C++】list容器功能模拟实现
介绍 上一次介绍了list队容器的迭代器模拟,这次模拟实现list的简单功能,尤其要注意构造函数、析构函数、以及赋值运算符重载的实现。 list容器需要接纳所有类型的数据,因此,结构设置与迭代器设置同理,需要引入结点&…...

linux 安装ffmpeg
一、下载 ffmpeg-4.3.1 下载地址:链接:https://pan.baidu.com/s/1xbkpHDfIWSCbHFGJJHSQcA 提取码:3eil 二、上传到服务器root目录下 三、给ffmpeg-4.3.1 读写权限 chmod -R 777 /root/ffmpeg-4.3.1 四、创建软连接 1.进入/bin 目录 2.…...

激光雷达行业梳理2-产业链、公司、未来展望
四、产业链及竞争格局 激光雷达产业链可以分为上游(光学和电子元器件)、中游(集成激光雷达)、下游(不同应用场景)。其中 上游即激光发射、激光接收、扫描系统和信息处理四大部分,主要包括激光器…...

Java 设计者模式以及与Spring关系(四) 代理模式
目录 简介: 23设计者模式以及重点模式 代理模式(Proxy Pattern) 静态代理示例 spring中应用 动态代理 1.基于JDK的动态代理 target.getClass().getInterfaces()作用 内名内部类写法(更简洁,但不推荐) 2.基于CGLIB实现 spring中应用 …...

PHP编程实践:实际商品价格数据采集
引言 在电子商务领域,对商品价格进行数据采集和对比是一项常见的需求。本文将介绍如何使用PHP编程语言实现对1688和淘宝商品价格数据的采集和对比,帮助读者了解实际的编程实践过程。 一、数据采集原理 数据采集是指从互联网上获取数据的过程ÿ…...

有效防范网络风险的关键措施
在数字化时代,企业面临着日益复杂和频繁的网络风险。提高员工的网络安全意识是防范网络威胁的关键一步。本文将探讨企业在提升网络安全意识方面可以采取的措施,以有效预防潜在的网络风险。 1. 开展网络安全培训:企业应定期组织网络安全培训&…...

Spring Boot整合webservice
Spring Boot整合webservice 前言1.整合依赖2.建立暴露接口2.实现类 3.发布服务4.查看打完收工! 前言 工作中遇到的问题,由于下游系统属于第三方系统,使用的是soap webservice,同时也在开发,虽然也发布了一套webservic…...
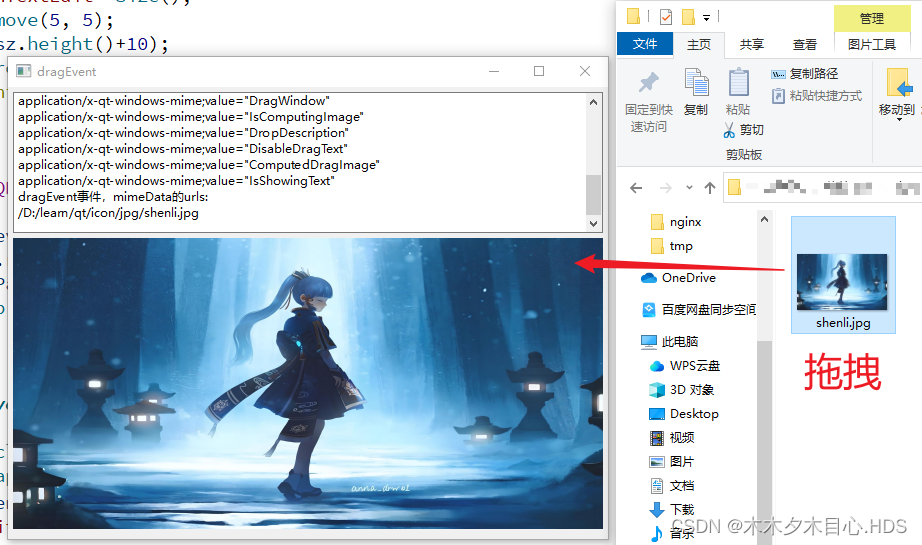
Qt拖拽事件简单实现
1.相关说明 重写resizeEvent(这个按需重写)、dragEnterEvent(拖拽事件函数)、dropEvent(放下事件函数),可以将本地图片拖拽到label标签中 2.相关界面 3.相关代码 #include "widget.h" #include "ui_widget.h" #include <QDragEnterEvent>…...
上门回收小程序,打造回收新模式
近年来,我国一直秉持着环保绿色的发展理念,为了减少资源浪费,旧物回收成为了人们处理废弃物品的方式。目前,我国回收市场规模大约能达到3.58亿元,在我国经济的稳定增长和环保意识的提高下,回收市场规模还将…...

unity项目《样板间展示》开发:火焰和UI设计
第二章:火焰和UI设计 前言一、火焰模型管理灶台火焰壁炉火焰 二、电视机播放三、UI设计结语 前言 这次带大家从0到1做一个unity项目:《样板间展示》。 顾名思义,项目内容是展示样板间,即玩家可以与房间中的物体、家具进行交互。 至…...

即插即用篇 | UniRepLKNet:用于音频、视频、点云、时间序列和图像识别的通用感知大卷积神经网络 | DRepConv
大卷积神经网络(ConvNets)近来受到了广泛研究关注,但存在两个未解决且需要进一步研究的关键问题。1)现有大卷积神经网络的架构主要遵循传统ConvNets或变压器的设计原则,而针对大卷积神经网络的架构设计仍未得到解决。2)随着变压器在多个领域的主导地位,有待研究ConvNets…...

MPU6050传感器—姿态检测
本节主要介绍以下内容: 姿态检测的基本概念 姿态传感器的工作原理及参数 MPU6050传感器介绍 实验:获取MPU6050原始数据 实验:移植官方DMP例程 一、姿态检测基本概念 1.1 姿态 在飞行器中,飞机姿态是非常重要的参数&#x…...

PaddleOCR封装,在线服务化部署实战(python部署,超新手教程)
OCR,即光学字符识别(Optical Character Recognition),是一种将图像中的文字转换为机器编码文字的技术。这种技术可以识别和转换各种来源的文本,包括扫描文档、照片中的文字、手写笔记等。光学字符识别(OCR&…...
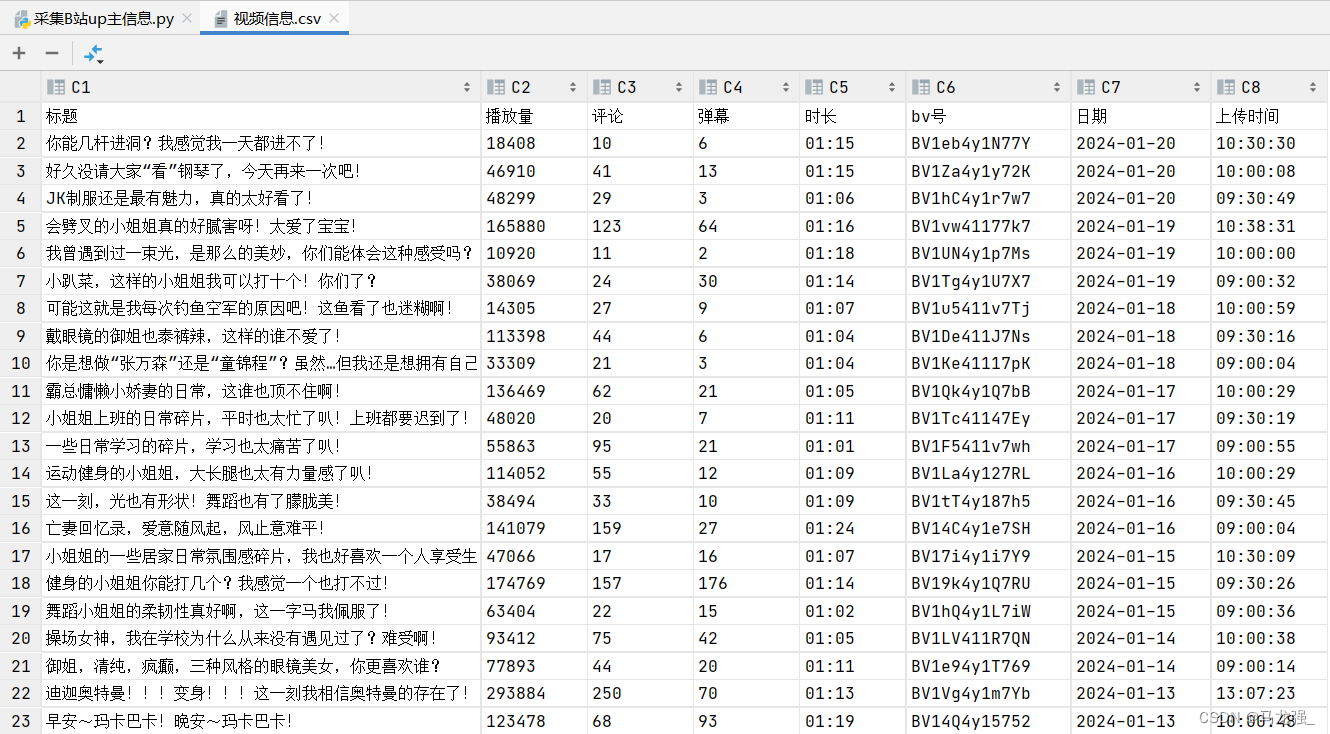
采集B站up主视频信息
一、网页信息(示例网址:https://space.bilibili.com/3493110839511225/video) 二、查看响应数据 三、查看数据包内容 四、相关代码(代码内容未进行翻页爬取) # Time: 2024/1/19 16:42 # Author: 马龙强 # File: 采集B…...
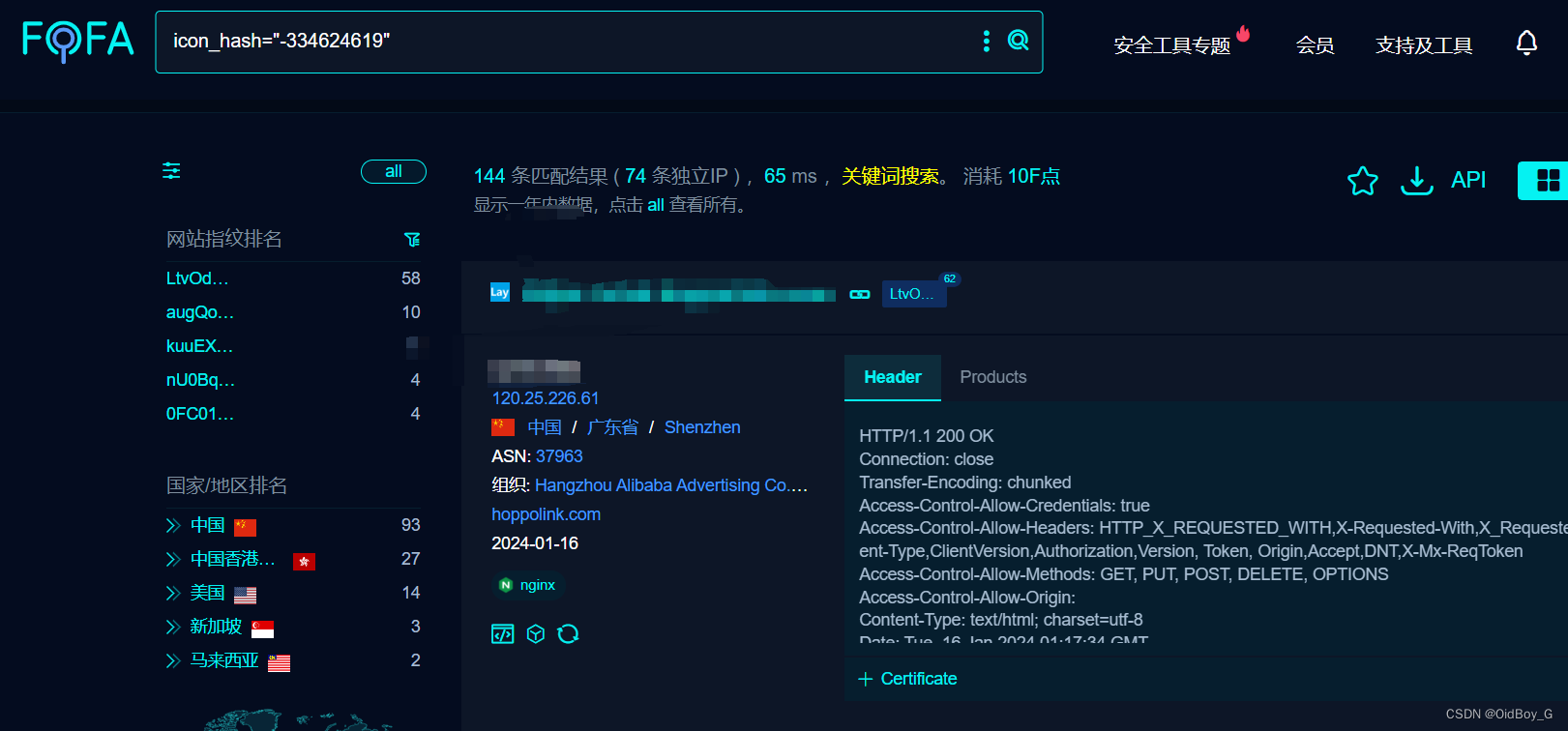
Laykefu客服系统 任意文件上传漏洞复现
0x01 产品简介 Laykefu 是一款基于workerman+gatawayworker+thinkphp5搭建的全功能webim客服系统,旨在帮助企业有效管理和提供优质的客户服务。 0x02 漏洞概述 Laykefu客服系统/admin/users/upavatar.html接口处存在文件上传漏洞,而且当请求中Cookie中的”user_name“不为…...

《幻兽帕鲁》服务器该如何选购
幻兽帕鲁作为目前火爆的一款游戏,幻兽帕鲁的服务器要能够承受其强大的力量和能力,需要具备一定的配置和性能。因此针对<幻兽帕鲁>这款游戏我们来总结一些可能用于承载幻兽帕鲁的服务器类型: 高性能服务器:幻兽帕鲁的能力强大,可能需要…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...
