Bit Extraction and Bootstrapping for BGV/BFV
参考文献:
- [GHS12] Gentry C, Halevi S, Smart N P. Better bootstrapping in fully homomorphic encryption[C]//International Workshop on Public Key Cryptography. Berlin, Heidelberg: Springer Berlin Heidelberg, 2012: 1-16.
- [AP13] Alperin-Sheriff J, Peikert C. Practical bootstrapping in quasilinear time[C]//Annual Cryptology Conference. Berlin, Heidelberg: Springer Berlin Heidelberg, 2013: 1-20.
- [HS15] Halevi S, Shoup V. Bootstrapping for helib[J]. Journal of Cryptology, 2021, 34(1): 7.
- [CH18] Chen H, Han K. Homomorphic lower digits removal and improved FHE bootstrapping[C]//Annual International Conference on the Theory and Applications of Cryptographic Techniques. Cham: Springer International Publishing, 2018: 315-337.
- [GV23] Geelen R, Vercauteren F. Bootstrapping for BGV and BFV Revisited[J]. Journal of Cryptology, 2023, 36(2): 12.
文章目录
- GHS12
- Extracting the Top and Bottom Bits
- Lower-Degree Bit Extraction
- Bootstrapping with Packed Ciphertexts
- AP13
- HS15
- Hypercube structure
- Recryption Procedure
- Linear Transformations
- Parameters for Recryption
- CH18
- Digit Removal Algorithm
- Bootstrapping for FV and BGV
GHS12
多项式环 R : = Z [ X ] / ( F ( X ) ) R:=\mathbb Z[X]/(F(X)) R:=Z[X]/(F(X)),明文空间 p = 2 p=2 p=2,密文模数 gcd ( q , p ) = 1 \gcd(q,p)=1 gcd(q,p)=1,BGV 方案的解密分为三步:
- 计算私钥上的依赖密文的线性函数, Z = ⟨ c , s ⟩ m o d F Z=\langle c,s\rangle \bmod F Z=⟨c,s⟩modF
- 模掉密文模数, e = [ Z ] q e = [Z]_q e=[Z]q,这里 e = 2 u + μ ∈ R e=2u+\mu \in R e=2u+μ∈R
- 提取最低比特位, μ = [ e ] 2 \mu = [e]_2 μ=[e]2
[GHS12] 的一个重要观察是:如果 q = 2 r + 1 q=2^r+1 q=2r+1,那么解密过程可以简化。我们用 z [ i ] z[i] z[i] 表示整系数 z z z 的第 i i i 个比特(索引从 0 0 0 开始),用 z [ j : i ] z[j:i] z[j:i] 表示截取部分比特。
-
假如 Z Z Z 某个系数 z z z 的规模远小于 q 2 q^2 q2 量级(这是合理的,因为 c c c 的系数规模仅为 q q q 量级),那么必定有
[ [ z ] q ] 2 = [ z [ r − 1 : 0 ] − z [ 2 r − 1 : r ] ] 2 = [ z [ 0 ] − z [ r ] ] 2 = z [ r ] ⊕ z [ 0 ] \begin{aligned} \big[[z]_q\big]_2 &= \big[z[r-1:0] - z[2r-1:r]\big]_2\\ &= \big[z[0] - z[r]\big]_2\\ &= z[r] \oplus z[0] \end{aligned} [[z]q]2=[z[r−1:0]−z[2r−1:r]]2=[z[0]−z[r]]2=z[r]⊕z[0] -
(仅在自举时)采用新的明文空间 p ′ = 2 r + 1 p'=2^{r+1} p′=2r+1,我们将私钥 s s s 作为空间 R p ′ R_{p'} Rp′ 中的明文,加密为 BK 公开
-
同态计算出 Z ( m o d p ′ ) Z \pmod{p'} Z(modp′),它的各个系数恰为 z [ r : 0 ] z[r:0] z[r:0],我们只需再同态提取出 z [ r ] z[r] z[r] 和 z [ 0 ] z[0] z[0] 即可
现在的问题就是,如何同态提取出 R p ′ R_{p'} Rp′ 的 MSB 和 LSB?
Extracting the Top and Bottom Bits
[GHS12] 的另一个重要观察是:因为 p ′ p' p′ 是二的幂次,从而有
[ z 2 ] p ′ = [ ( z [ r : 1 ] ⋅ 2 k + z [ 0 ] ) 2 ] p ′ = [ z [ r : 1 ] 2 ⋅ 2 2 k + z [ r : 1 ] ⋅ z [ 0 ] ⋅ 2 k + 1 + z [ 0 ] ] p ′ = [ z [ r : 1 ] 2 ⋅ 2 k − 1 + z [ r : 1 ] ⋅ z [ 0 ] ] p ′ / 2 k + 1 ⋅ 2 k + 1 + z [ 0 ] \begin{aligned} \big[z^2\big]_{p'} &= \big[(z[r:1] \cdot 2^{k} + z[0])^2\big]_{p'}\\ &= \big[z[r:1]^2 \cdot 2^{2k} + z[r:1] \cdot z[0] \cdot 2^{k+1} + z[0]\big]_{p'}\\ &= \big[z[r:1]^2 \cdot 2^{k-1} + z[r:1] \cdot z[0]\big]_{p'/2^{k+1}} \cdot 2^{k+1} + z[0] \end{aligned} [z2]p′=[(z[r:1]⋅2k+z[0])2]p′=[z[r:1]2⋅22k+z[r:1]⋅z[0]⋅2k+1+z[0]]p′=[z[r:1]2⋅2k−1+z[r:1]⋅z[0]]p′/2k+1⋅2k+1+z[0]
它保持 LSB 不变,在 LSB 的高位不断插入零。
因此,对于任意的整数 z = ∑ i = 0 r 2 i z [ i ] z=\sum_{i=0}^r 2^i z[i] z=∑i=0r2iz[i],初始化 w 0 : = z w_0:=z w0:=z,计算出
w i : = z − ∑ j = 0 i − 1 2 j w j 2 i − j ( m o d 2 r + 1 ) 2 i w_i := \frac{z-\sum_{j=0}^{i-1}2^jw_j^{2^{i-j}} \pmod{2^{r+1}}}{2^i} wi:=2iz−∑j=0i−12jwj2i−j(mod2r+1)
那么就有 w i [ 0 ] = z [ i ] , ∀ i w_i[0] = z[i],\forall i wi[0]=z[i],∀i,这便提取出了 MSB 和 LSB。其中的除法 a / 2 i a/2^i a/2i 是整除的,因此可以直接计算 c t ⋅ [ 2 − i ] q ct \cdot [2^{-i}]_{q} ct⋅[2−i]q 即可。副作用是噪声 p ′ u p'u p′u 也缩放为了 p ′ 2 − i u = 2 r − i + 1 u p'2^{-i}u = 2^{r-i+1}u p′2−iu=2r−i+1u(侵蚀明文空间高位),因此输出的是 w i ∈ Z 2 r − i + 1 w_i \in \mathbb Z_{2^{r-i+1}} wi∈Z2r−i+1,特别地 w 0 ∈ Z 2 r + 1 w_0 \in \mathbb Z_{2^{r+1}} w0∈Z2r+1 以及 w r = Z 2 w_r = \mathbb Z_{2} wr=Z2。当然,这并不影响两者的加和,
w r + w 0 ≡ z [ r ] ⊕ z [ 0 ] ∈ Z 2 w_r+w_0 \equiv z[r] \oplus z[0] \in \mathbb Z_2 wr+w0≡z[r]⊕z[0]∈Z2
算法如图所示:

Lower-Degree Bit Extraction
由于自举需要的明文模数 p ′ = 2 r + 1 p'=2^{r+1} p′=2r+1 其规模依赖于密文模数 q = 2 r + 1 q=2^r+1 q=2r+1,参数 r r r 越小,则比特提取程序的计算速度和乘法深度都可以降低。[GHS12] 给出了优化技术:在密文 ( c 0 , c 1 ) ( m o d q ) (c_0,c_1) \pmod q (c0,c1)(modq) 上添加一些 q q q 的倍数,使得它们的系数都整除 2 r ′ , 1 ≤ r ′ < r 2^{r'},1\le r'<r 2r′,1≤r′<r,记为 ( c 0 ′ , c 1 ′ ) (c_0',c_1') (c0′,c1′),易知它加密相同的消息。
只要 c t ′ ct' ct′ 的系数依旧远小于 q 2 q^2 q2 规模,令 Z ′ = c 0 ′ + c 1 ′ ⋅ s Z'=c_0'+c_1' \cdot s Z′=c0′+c1′⋅s,易知也有 2 r ′ ∣ Z ′ 2^{r'}|Z' 2r′∣Z′,因此 z ′ [ 0 ] = 0 z'[0]=0 z′[0]=0,从而有 μ = z ′ [ r ] \mu = z'[r] μ=z′[r]。进一步的,我们将 ( c 0 ′ , c 1 ′ ) (c_0',c_1') (c0′,c1′) 整除(等价于求逆)掉 2 r ′ 2^{r'} 2r′ 成为 ( c 0 ′ ′ , c 1 ′ ′ ) (c_0'',c_1'') (c0′′,c1′′),那么就有 μ = z ′ ′ [ r − r ′ ] \mu = z''[r-r'] μ=z′′[r−r′],现在只需要明文模数 p ′ = 2 r − r ′ + 1 p'=2^{r-r'+1} p′=2r−r′+1 即可。
Bootstrapping with Packed Ciphertexts
由于自举时采用明文空间 R p ′ R_{p'} Rp′,其中 p ′ = 2 r + 1 p'=2^{r+1} p′=2r+1 是二的幂次(而非素数),因此 SIMD 技术存在一些改变。任意素数 p p p(包括 p = 2 p=2 p=2),[GHS12] 将空间 Z / p t Z \mathbb Z/p^t\mathbb Z Z/ptZ 视为 p p p-adic integers 的精度 t t t 近似(局部域——p-进数),定义符号
Z p : = { ∑ i = 0 ∞ a i ⋅ p i ∣ a i ∈ F p } \mathbb Z_p := \left\{ \sum_{i=0}^\infty a_i \cdot p^i \Big| a_i \in \mathbb F_p \right\} Zp:={i=0∑∞ai⋅pi∣∣∣ai∈Fp}
它是 p p p 上的形式幂级数,表示全部的 p p p-adic integers。当 t t t 趋于无穷, Z / p t Z \mathbb Z/p^t\mathbb Z Z/ptZ 的极限就是 Z p \mathbb Z_p Zp,因此 R p t R_{p^t} Rpt 是 R p ∞ R_{p^\infty} Rp∞ 的精度 t t t 近似。
Hensel Lifting:素数 p p p,整数 t ≥ 1 t \ge 1 t≥1,假设 G , H , F ∈ Z [ X ] G,H,F \in \mathbb Z[X] G,H,F∈Z[X] 是首一多项式,并且满足
- 在模数 p p p 下, G , H G,H G,H 互素
- G ⋅ H = F ( m o d p t ) G \cdot H = F \pmod{p^t} G⋅H=F(modpt)
那么存在首一多项式 G ˉ , H ˉ ∈ Z [ X ] \bar G,\bar H \in \mathbb Z[X] Gˉ,Hˉ∈Z[X],使得
- G ˉ ≡ G ( m o d p t ) \bar G \equiv G \pmod{p^t} Gˉ≡G(modpt) 以及 H ˉ ≡ H ( m o d p t ) \bar H \equiv H \pmod{p^t} Hˉ≡H(modpt)
- G ˉ ⋅ H ˉ = F ( m o d p t + 1 ) \bar G \cdot \bar H = F \pmod{p^{t+1}} Gˉ⋅Hˉ=F(modpt+1)
这个定理可以用于将 p p p 下的解,提升到任意的 p t p^t pt 下的解(具体怎么构造的?论文没写):
- 模 p p p 平方自由的多项式 F F F,它在模 p t p^t pt 下不可约,当仅当它在模 p p p 下不可约
- 模 p p p 平方自由的多项式 F F F,它在模 p t p^t pt 下的分解,由它在模 p p p 下的分解唯一确定
这意味这,任意的 t ≥ 1 t \ge 1 t≥1, F ( X ) ( m o d p t ) F(X) \pmod{p^t} F(X)(modpt) 的明文槽,与 F ( X ) ( m o d p ) F(X) \pmod{p} F(X)(modp) 的基本相同。
给定分圆多项式 Φ m ( X ) \Phi_m(X) Φm(X),假设 p ( m o d m ) p \pmod m p(modm) 的乘法阶是 d d d,那么它在模 p p p 下可以分解为 l = ϕ ( m ) / d l=\phi(m)/d l=ϕ(m)/d 个不同的首一不可约因子,
Φ m ( X ) = ∏ j = 0 l = 1 F j ( X ) ( m o d p ) \Phi_m(X) = \prod_{j=0}^{l=1} F_j(X) \pmod{p} Φm(X)=j=0∏l=1Fj(X)(modp)
然后利用 Hensel Lifting 定理,可以获得提升后的分解:
Φ m ( X ) = ∏ j = 0 l = 1 F ˉ j ( X ) ( m o d p t ) \Phi_m(X) = \prod_{j=0}^{l=1} \bar F_j(X) \pmod{p^t} Φm(X)=j=0∏l=1Fˉj(X)(modpt)
其中 F ˉ j ≡ F j ( m o d p ) \bar F_j \equiv F_j \pmod{p} Fˉj≡Fj(modp) 是模 p t p^t pt 下首一不可约多项式。根据 CRT,明文槽的结构为:
( Z / p t Z ) [ X ] / ( F ˉ j ( X ) ) ≅ ( Z / p t Z ) [ X ] / ( G ( X ) ) , ∀ j = 0 , ⋯ , l − 1 (\mathbb Z/p^t\mathbb Z)[X]/(\bar F_j(X)) \cong (\mathbb Z/p^t\mathbb Z)[X]/(G(X)), \forall j=0,\cdots,l-1 (Z/ptZ)[X]/(Fˉj(X))≅(Z/ptZ)[X]/(G(X)),∀j=0,⋯,l−1
其中 G ( X ) G(X) G(X) 是任意的 F p \mathbb F_p Fp 下 d d d 次不可约多项式,可以简单地取为 F ˉ 0 ( X ) \bar F_0(X) Fˉ0(X)。简记 R p t , d R_{p^t,d} Rpt,d 是这个明文槽代数结构,它包含了 d d d 次本原单位根。 G a l ( R p t ) ≅ ( Z / m Z ) ∗ \mathcal{Gal}(R_{p^t}) \cong (\mathbb Z/m\mathbb Z)^* Gal(Rpt)≅(Z/mZ)∗,所有自同构形如 X ↦ X i X \mapsto X^i X↦Xi,
- 由 p p p 生成的 d d d 阶(乘法)循环群,它们是 Frobenius maps,独立地作用在各个槽上
- 商群 ( Z / m Z ) ∗ / ( p ) (\mathbb Z/m\mathbb Z)^*/(p) (Z/mZ)∗/(p) 的阶 l = ϕ ( m ) / d l=\phi(m)/d l=ϕ(m)/d,它们组成了集合 [ l ] [l] [l] 上的 sharply transitive permutations,可用于实现明文槽直接的任意置换(Benes Network)
利用这些自同构,可以实现批处理的比特提取(相位的每个系数)。自举基本框架:
- 同态计算线性函数,获得 Z ( X ) ∈ R 2 r + 1 Z(X) \in R_{2^{r+1}} Z(X)∈R2r+1
- 同态计算 Inv-DFT,将 Z ( X ) Z(X) Z(X) 的各个系数转换到明文槽。实际上系数 z ∈ Z 2 r + 1 z \in \mathbb Z_{2^{r+1}} z∈Z2r+1 仅存放在 R 2 r + 1 , d R_{2^{r+1},d} R2r+1,d 的基环上(每个密文仅包含 l l l 个槽,共需要 d d d 个密文)
- 同态计算比特提取程序,计算出 z [ r ] ⊕ z [ 0 ] ∈ Z 2 z[r] \oplus z[0] \in \mathbb Z_2 z[r]⊕z[0]∈Z2,它放在了 R 2 , d R_{2,d} R2,d 的基环上
- 同态计算 DFT,将明文槽中的 μ i \mu_i μi 打包为多项式 μ ( X ) ∈ R 2 \mu(X) \in R_2 μ(X)∈R2
AP13
[AP13] 采用了 [GHS12] 的简单解密方法,但是没有使用 Benes Network 去执行线性变换,而是利用了 Ring/Feild-Switching 技术,利用 Trace 在分圆塔上移动,实现线性变换的张量分解(tensor decomposition)。然而 [HS15] 指出:由于自举结果只有较少的 Level,因此张量分解也只能是粗粒度的,从而不消耗过多的 Level;同时为了安全性,因为噪声是超多项式的小,切换后的 Ring 应当维度很大;并且使用 [HS18] 的 BSGS 矩阵向量算法后,自举开销主要是比特提取,继续优化线性变换的意义不大。
HS15
[HS15] 最早发在 2015 美密上,之后整合了 [HS18] 的线性变换技术以及 [CH18] 的 “薄” 自举技术,还有一些其他的小优化,重新发表在 2021 密码学杂志上。
[HS15] 将 [GHS12] 的自举技术从只能处理特征 p = 2 p=2 p=2,给推广到可以处理任意的素数特征。首先我们确定整数 z z z 的 base- p p p representation,
-
p = 2 p=2 p=2 时,符号 [ z ] 2 [z]_2 [z]2 取值范围 { 0 , 1 } \{0,1\} {0,1},二补数表示(2’s-complement representation of signed integers)
z [ j : i ] = ∑ k = i j − 1 2 k − i z [ k ] − 2 j − i z [ j ] z[j:i] = \sum_{k=i}^{j-1}2^{k-i}z[k] - 2^{j-i}z[j] z[j:i]=k=i∑j−12k−iz[k]−2j−iz[j]
其中 z [ k ] ∈ { 0 , 1 } z[k] \in \{0,1\} z[k]∈{0,1},换句话说 MSB 表示了一个很大的负数 -
p > 2 p>2 p>2 时,符号 [ z ] p [z]_p [z]p 取值范围 [ − ( p − 1 ) / 2 , ( p − 1 ) / 2 ] [-(p-1)/2,(p-1)/2] [−(p−1)/2,(p−1)/2],平衡 p p p 进制表示( balanced base-p representation of signed integers)
z [ j : i ] = ∑ k = i j p k − i z [ k ] z[j:i] = \sum_{k=i}^{j}p^{k-i}z[k] z[j:i]=k=i∑jpk−iz[k]
其中 z [ k ] ∈ [ − ( p − 1 ) / 2 , ( p − 1 ) / 2 ] z[k] \in [-(p-1)/2,(p-1)/2] z[k]∈[−(p−1)/2,(p−1)/2]
Hypercube structure
在 HElib 实现中的本地明文空间是 R p r R_{p^r} Rpr,其中 p p p 是素数, r r r 是 Hensel Lifting 参数。密文模数 q q q,私钥 s ∈ R s \in R s∈R,密文 ( c 0 , c 1 ) ∈ R q (c_0,c_1) \in R_q (c0,c1)∈Rq,那么有 [ c 0 + c 1 ⋅ s ] q = m + p r e ∈ R [c_0+c_1 \cdot s]_q = m+p^re \in R [c0+c1⋅s]q=m+pre∈R,其中 e ∈ R e \in R e∈R 是短噪声, m ∈ R p r m \in R_{p^r} m∈Rpr 是明文。
利用 Hensel Lifting 以及 CRT,分解出 Φ m ( X ) = ∏ i = 1 k F i ( X ) ( m o d p r ) \Phi_m(X) = \prod_{i=1}^k F_i(X) \pmod{p^r} Φm(X)=∏i=1kFi(X)(modpr),每个因子 F i F_i Fi 的度数都是 p ( m o d m ) p \pmod m p(modm) 的乘法阶 d d d,个数为 k = ϕ ( m ) / d k=\phi(m)/d k=ϕ(m)/d,同构为
R p r ≅ ⨁ i = 1 k Z [ X ] / ( p r , F i ( X ) ) R_{p^r} \cong \bigoplus_{i=1}^k \mathbb Z[X]/(p^r,F_i(X)) Rpr≅i=1⨁kZ[X]/(pr,Fi(X))
我们定义 E : = Z [ X ] / ( p r , F 1 ( X ) ) E := \mathbb Z[X]/(p^r,F_1(X)) E:=Z[X]/(pr,F1(X)) 是明文槽的代数结构,令 ζ \zeta ζ 是 m m m-th 本原单位根 X X X 在 E E E 中所在的剩余类,于是有 E = Z p r [ ζ ] E = \mathbb Z_{p^r}[\zeta] E=Zpr[ζ]
假设 S ⊆ Z S \subseteq \mathbb Z S⊆Z 是商群 Z m ∗ / ( p ) \mathbb Z_m^*/(p) Zm∗/(p) 的完全代表(complete system of representatives), ∣ S ∣ = k |S|=k ∣S∣=k,那么就有如下的同构映射,
R p r → ⨁ h ∈ S E α ↦ { α ( ζ h ) } h ∈ S \begin{aligned} R_{p_r} &\to \bigoplus_{h \in S} E\\ \alpha &\mapsto \{\alpha(\zeta^h)\}_{h \in S} \end{aligned} Rprα→h∈S⨁E↦{α(ζh)}h∈S
自同构映射 τ j : α ( X ) ↦ α ( X j ) , ∀ j ∈ Z m ∗ \tau_j: \alpha(X) \mapsto \alpha(X^j), \forall j \in \mathbb Z_m^* τj:α(X)↦α(Xj),∀j∈Zm∗,它们诱导了明文槽的超立方结构:HElib 记录了超立方基(hypercube basis ) g 1 , ⋯ , g n ∈ Z m ∗ g_1,\cdots,g_n \in \mathbb Z_m^* g1,⋯,gn∈Zm∗,以及它们的阶 l 1 , ⋯ , l n l_1,\cdots,l_n l1,⋯,ln(并非是 Z m ∗ \mathbb Z_m^* Zm∗ 中的乘法阶),使得 Z m ∗ / ( p ) \mathbb Z_m^*/(p) Zm∗/(p) 的代表为
S : = { g 1 e 1 ⋯ g n e n ∣ 0 ≤ e i < l i } S := \{g_1^{e_1} \cdots g_n^{e_n} | 0 \le e_i < l_i\} S:={g1e1⋯gnen∣0≤ei<li}
那么,每个元素 h h h(明文槽)都对应一个索引 ( e 1 , ⋯ , e n ) (e_1,\cdots,e_n) (e1,⋯,en),我们将 “固定其他坐标遍历 e i e_i ei 坐标的那些槽” 称为维度 i i i 上的超列(hypercolumn)。我们将超列中的每个槽 ( ⋯ , e i , ⋯ ) (\cdots,e_i,\cdots) (⋯,ei,⋯) 映射到 ( ⋯ , e i + v ( m o d l i ) , ⋯ ) (\cdots,e_i+v \pmod{l_i},\cdots) (⋯,ei+v(modli),⋯) 称为维度 i i i 上的旋转。具体的实现为:
- 假如 g i g_i gi 在 Z m ∗ \mathbb Z_m^* Zm∗ 上的乘法阶恰为 l i l_i li,那么定义 ρ i v ( α ) : = τ g i v ( α ) \rho_i^v(\alpha) := \tau_{g_i^v}(\alpha) ρiv(α):=τgiv(α),我们称 i i i 是 “good dimension”(只需一次自同构)
- 假如 g i g_i gi 在 Z m ∗ \mathbb Z_m^* Zm∗ 上的乘法阶不是 l i l_i li,那么定义 ρ i v ( α ) : = τ g i v ( mask ⋅ α ) + τ g i v − l i ( ( 1 − mask ) ⋅ α ) \rho_i^v(\alpha) := \tau_{g_i^v}(\text{mask} \cdot \alpha) + \tau_{g_i^{v-l_i}}((1-\text{mask}) \cdot \alpha) ρiv(α):=τgiv(mask⋅α)+τgiv−li((1−mask)⋅α),我们称 i i i 是 “bad dimension”(需要两次自同构)
除了这些 rotate1D 自同构,循环群 ( p ) (p) (p) 对应的那些自同构是 Frobenius map,可用于计算明文槽本身的线性变换。假设 M M M 是明文槽 E E E 上的 Z p r \mathbb Z_{p^r} Zpr-线性变换(注意区分各个槽之间的 E E E-线性变换),那么总存在唯一的常数集 θ 0 , ⋯ , θ d − 1 \theta_0,\cdots,\theta_{d-1} θ0,⋯,θd−1,使得 M M M 写为如下的线性化多项式(linearized polynomials),
M ( a ) = ∑ i = 0 d − 1 θ i τ p i ( a ) , ∀ a ∈ E M(a) = \sum_{i=0}^{d-1} \theta_i \tau_p^i(a), \forall a \in E M(a)=i=0∑d−1θiτpi(a),∀a∈E
给定 M M M 的描述(比如 power basis 的像),可以通过求解模 p p p 下的线性方程组,获得 mod- p p p solutions,然后利用 Hensel Lifting 提升到模 p r p^r pr 下即可获得 θ i \theta_i θi 的具体值。对于不同的明文槽,可以执行不同的变换 M M M;我们计算出它们的常数后,打包为 d d d 个多项式,用于同态计算明文槽内部的线性变换。
Recryption Procedure
[HS15] 采取了 [GHS12] 的自举框架:明文模数 p r p^r pr,密文模数 q = p e + 1 q=p^e+1 q=pe+1,自举需要的明文模数为 p e + r p^{e+r} pe+r,那么
- 首先计算 u = [ ⟨ s k , c t ⟩ ] p e + r u = [\langle sk,ct \rangle]_{p^{e+r}} u=[⟨sk,ct⟩]pe+r
- 然后计算 m = u [ r − 1 : 0 ] − u [ e + r − 1 : e ] ( m o d p r ) m = u[r-1:0] - u[e+r-1:e] \pmod{p^r} m=u[r−1:0]−u[e+r−1:e](modpr)
为了降低乘法深度,可以设置中等规模参数 r ≤ e ′ < e r \le e' <e r≤e′<e,使得密文 c t ′ ct' ct′ 可被 p e ′ p^{e'} pe′ 整除,从而我们计算 u ′ = [ ⟨ s k , c t ′ / p e ′ ⟩ ] p e + r u' = [\langle sk,ct'/p^{e'} \rangle]_{p^{e+r}} u′=[⟨sk,ct′/pe′⟩]pe+r,然后输出 m = − u ′ [ e − e ′ + r − 1 : e − e ′ ] ( m o d p r ) m = -u'[e-e'+r-1:e-e'] \pmod{p^r} m=−u′[e−e′+r−1:e−e′](modpr)
[GHS12] 的 ”通过平方插入零“ 的技巧仅适用于 p = 2 p=2 p=2 的情况,[HS15] 给出了更一般的 Lifting Polynomials,适用于任意的 p r p^r pr 情况。由于 [HS15] 采取了带符号的二补数和平衡进制表示,因此解密公式略有不同。
Simpler Decryption Formula:对于任意的素数 p > 1 p>1 p>1,整数 e > r ≥ 1 , q = p e + 1 e>r\ge1,\,\, q=p^e+1 e>r≥1,q=pe+1,假设 z z z 是满足 z / q z/q z/q 和 [ z ] q [z]_q [z]q 规模都远小于 q q q 的整数,具体来说, ∣ z / q ∣ + ∣ [ z ] q ∣ ≤ ( q − 1 ) / 2 |z/q|+|[z]_q| \le (q-1)/2 ∣z/q∣+∣[z]q∣≤(q−1)/2,那么
- 当 p = 2 p=2 p=2 时, [ z ] q = z [ r − 1 : 0 ] − z [ e + r − 1 : e ] − z [ e − 1 ] ( m o d 2 r ) [z]_q = z[r-1:0] - z[e+r-1:e] - z[e-1] \pmod{2^r} [z]q=z[r−1:0]−z[e+r−1:e]−z[e−1](mod2r)
- 当 p > 2 p>2 p>2 时, [ z ] q = z [ r − 1 : 0 ] − z [ e + r − 1 : e ] ( m o d p r ) [z]_q = z[r-1:0] - z[e+r-1:e] \pmod{p^r} [z]q=z[r−1:0]−z[e+r−1:e](modpr)
Reduce the number of digits:对于任意的整数 e ′ ≥ 1 e'\ge 1 e′≥1 以及 q > p > 1 q>p>1 q>p>1,使得 q ≡ 1 ( m o d p e ′ ) q \equiv 1 \pmod{p^{e'}} q≡1(modpe′),任给整数 z z z 总存在 ∣ v ∣ ≤ p e ′ / 2 |v| \le p^{e'}/2 ∣v∣≤pe′/2,它使得 z + v ⋅ q ≡ 0 ( m o d p e ′ ) z+v\cdot q \equiv 0 \pmod{p^{e'}} z+v⋅q≡0(modpe′)
The digit-extraction procedure:对于任意的素数 p p p 和指数 e ≥ 1 e \ge 1 e≥1,任意的形如 z = z 0 + p e z 1 , z 0 ∈ [ p ] , z 1 ∈ Z z=z_0+p^ez_1,\,\, z_0 \in [p], z_1 \in \mathbb Z z=z0+pez1,z0∈[p],z1∈Z 的整数,满足 z p = z 0 ( m o d p ) z^p=z_0 \pmod{p} zp=z0(modp) 以及 z p = z 0 p ( m o d p e + 1 ) z^p = z_0^p \pmod{p^{e+1}} zp=z0p(modpe+1)
由于 z p ( m o d p e + 1 ) z^p \pmod{p^{e+1}} zp(modpe+1) 仅依赖于 z 0 = [ z ] p e ∈ [ p ] z_0=[z]_{p^e} \in [p] z0=[z]pe∈[p] 的值,因此可以遍历 z 0 z_0 z0 计算出 z p ( m o d p e + 1 ) z^p \pmod{p^{e+1}} zp(modpe+1) 的各个数位,然后采取拉格朗日插值公式( f i ( z 0 ) = z p [ i ] f_i(z_0)=z^p[i] fi(z0)=zp[i]),计算出 f 1 , f 2 , ⋯ f_1,f_2,\cdots f1,f2,⋯ 序列(有限个非凡的,后续的都是 f i = 0 f_i=0 fi=0),它们的度数至多为 p − 1 p-1 p−1。对于任意的 e ≥ 1 e \ge 1 e≥1 和整数 z = z 0 + p e z 1 , z 0 ∈ [ p ] , z 1 ∈ Z z=z_0+p^ez_1,\,\, z_0 \in [p], z_1 \in \mathbb Z z=z0+pez1,z0∈[p],z1∈Z,总满足
z p = z 0 + ∑ i = 1 e f i ( z 0 ) p i ( m o d p e + 1 ) z^p = z_0 + \sum_{i=1}^e f_i(z_0)p^i \pmod{p^{e+1}} zp=z0+i=1∑efi(z0)pi(modpe+1)
因此,对于任意的 e ≥ 1 e \ge 1 e≥1,我们定义 deg = p \deg=p deg=p 的多项式:
F e ( X ) = X p − ∑ i = 1 e f i ( X ) p i F_e(X) = X^p - \sum_{i=1}^e f_i(X)p^i Fe(X)=Xp−i=1∑efi(X)pi
对于任意的 1 ≤ e ′ ≤ e 1 \le e' \le e 1≤e′≤e,任给形如 z = z 0 + p e ′ z 1 , z 0 ∈ [ p ] , z 1 ∈ Z z=z_0+p^{e'}z_1,\,\, z_0 \in [p], z_1 \in \mathbb Z z=z0+pe′z1,z0∈[p],z1∈Z 的整数,都有 F e ( z ) = z 0 ( m o d p e ′ + 1 ) F_e(z) = z_0 \pmod{p^{e'+1}} Fe(z)=z0(modpe′+1),这便实现了 “高位插入零” 的效果。通过 F e F_e Fe 的复合迭代,它可以将 z 0 + p z 1 z_0+pz_1 z0+pz1 映射为 z 0 ( m o d p e + 1 ) z_0 \pmod{p^{e+1}} z0(modpe+1) ,从而实现 LSB 的提取。再将 LSB 不断移除,也可以实现 MSB 的提取。

特别地,对于 p = 2 , 3 p=2,3 p=2,3,恰好是 F e ( X ) = X p , ∀ e F_e(X)=X^p, \forall e Fe(X)=Xp,∀e,这便是 [GHS12] 所使用的平方技巧。
Linear Transformations
本地明文空间 Z p r [ X ] / ( Φ m ( X ) ) \mathbb Z_{p^r}[X]/(\Phi_m(X)) Zpr[X]/(Φm(X)),我们考虑 m m m 的分解 m 1 ⋯ m t m_1\cdots m_t m1⋯mt,它们两两互素(比如素数幂分解),那么 h ∈ Z m h \in \mathbb Z_m h∈Zm 可以写作 h = CRT ( h 1 , ⋯ , h t ) , h i ∈ [ m i ] h=\text{CRT}(h_1,\cdots,h_t), h_i \in [m_i] h=CRT(h1,⋯,ht),hi∈[mi]
商群 Z m ∗ / ( p ) \mathbb Z_{m}^*/(p) Zm∗/(p) 的超立方结构:
- 我们令 p ( m o d m 1 ) p\pmod{m_1} p(modm1) 的乘法阶是 d 1 d_1 d1,对于 i ≥ 2 i\ge 2 i≥2 定义 d i d_i di 是 p d 1 ⋯ d i − 1 ( m o d m i ) p^{d_1\cdots d_{i-1}} \pmod{m_i} pd1⋯di−1(modmi) 的乘法阶,那么 d : = d 1 ⋯ d t d:=d_1\cdots d_t d:=d1⋯dt 就是 d ( m o d m ) d \pmod{m} d(modm) 的乘法阶。
- 我们令 S i ⊆ [ m i ] S_i \subseteq [m_i] Si⊆[mi] 是商群 Z m i ∗ / ( p d 1 ⋯ d i − 1 ) \mathbb Z_{m_i}^*/(p^{d_1\cdots d_{i-1}}) Zmi∗/(pd1⋯di−1) 的完全代表,那么 S : = CRT ( S 1 , ⋯ , S t ) S:=\text{CRT}(S_1,\cdots,S_t) S:=CRT(S1,⋯,St) 就是 Z m ∗ / ( p ) \mathbb Z_{m}^*/(p) Zm∗/(p) 的完全代表。
现在我们需要将这里的 S : = CRT ( S 1 , ⋯ , S t ) S:=\text{CRT}(S_1,\cdots,S_t) S:=CRT(S1,⋯,St) 和前两节的 S : = { g 1 e 1 ⋯ g n e n ∣ 0 ≤ e i < l i } S := \{g_1^{e_1} \cdots g_n^{e_n} | 0 \le e_i < l_i\} S:={g1e1⋯gnen∣0≤ei<li} 统一起来,这限制了 m m m 的选取:
- 限制 m m m 及其分解,使得 Z m i ∗ / ( p d 1 ⋯ d i − 1 ) \mathbb Z_{m_i}^*/(p^{d_1\cdots d_{i-1}}) Zmi∗/(pd1⋯di−1) 是循环群,
- 生成元 g ˉ i ∈ [ m i ] \bar g_i \in [m_i] gˉi∈[mi],乘法阶 k i k_i ki
- 集合 S i : = { g ˉ i e i ∣ 0 ≤ e i < k i } S_i:=\{\bar g_i^{e_i}| 0\le e_i<k_i\} Si:={gˉiei∣0≤ei<ki}
- 定义 g i = CRT ( 1 , ⋯ , g ˉ i , ⋯ , 1 ) ∈ [ m ] g_i=\text{CRT}(1,\cdots,\bar g_i,\cdots,1) \in [m] gi=CRT(1,⋯,gˉi,⋯,1)∈[m] 是超立方基,那么 S S S 的那两种定义是同一个
- 限制 m m m 及其分解,使得 d 1 = d d_1=d d1=d 和 d 2 = ⋯ = d t = 1 d_2=\cdots=d_t=1 d2=⋯=dt=1,
- p p p 在 Z m 1 ∗ \mathbb Z_{m_1}^* Zm1∗ 的阶,就是 p p p 在 Z m ∗ \mathbb Z_m^* Zm∗ 的阶 d d d
- g i , ∀ i ≥ 2 g_i,\forall i\ge 2 gi,∀i≥2 在 Z m ∗ \mathbb Z_m^* Zm∗ 的阶,就是 g ˉ i \bar g_i gˉi 在 Z m i ∗ / ( p d ) = Z m i ∗ \mathbb Z_{m_i}^*/(p^d)=\mathbb Z_{m_i}^* Zmi∗/(pd)=Zmi∗ 的阶 k i k_i ki
- k 1 = ϕ ( m 1 ) / d k_1=\phi(m_1)/d k1=ϕ(m1)/d, k i = ϕ ( m i ) , ∀ i ≥ 2 k_i=\phi(m_i),\forall i\ge 2 ki=ϕ(mi),∀i≥2
[HS15] 将编码解码的线性变换视为多项式的多点求值。利用 [LPR13] 的 Powerful Basis,存在如下的同构:
R p r : = Z [ X ] / ( p r , Φ m ( X ) ) ≅ R p r ′ : = Z [ X 1 , ⋯ , X t ] / ( p r , Φ m 1 ( X ) , ⋯ , Φ m t ( X ) ) R_{p^r}:=\mathbb Z[X]/(p^r,\Phi_m(X)) \cong R_{p^r}':=\mathbb Z[X_1,\cdots,X_t]/(p^r,\Phi_{m_1}(X),\cdots,\Phi_{m_t}(X)) Rpr:=Z[X]/(pr,Φm(X))≅Rpr′:=Z[X1,⋯,Xt]/(pr,Φm1(X),⋯,Φmt(X))
其同构映射为 X i ↦ X m / m i X_i \mapsto X^{m/m_i} Xi↦Xm/mi。由于 E E E 包含 m m m-th 本原单位根 ζ \zeta ζ,我们定义 ζ i : = ζ m / m i \zeta_i:=\zeta^{m/m_i} ζi:=ζm/mi,那么 α ( ζ h ) = α ′ ( ζ 1 h 1 , ⋯ , ζ t h t ) \alpha(\zeta^h) = \alpha'(\zeta_1^{h_1},\cdots,\zeta_t^{h_t}) α(ζh)=α′(ζ1h1,⋯,ζtht),其中 h = CRT ( h 1 , ⋯ , h t ) ∈ S h=\text{CRT}(h_1,\cdots,h_t) \in S h=CRT(h1,⋯,ht)∈S,并且 h i = g i e i ∈ S i h_i=g_i^{e_i} \in S_i hi=giei∈Si
现在,我们对 α ′ ( X 1 , ⋯ , X t ) \alpha'(X_1,\cdots,X_t) α′(X1,⋯,Xt) 在多个点 ( ζ 1 h 1 , ⋯ , ζ t h t ) (\zeta_1^{h_1},\cdots,\zeta_t^{h_t}) (ζ1h1,⋯,ζtht) 上求值(效果是 Slot-to-Coeff):
α ′ ( X 1 , ⋯ , X t ) = ∑ j 1 , j 2 , ⋯ , j t c j 1 , j 2 , ⋯ , j t ⋅ X 1 j 1 X 2 j 2 ⋯ X t j t = ∑ j 2 , ⋯ , j t ( ∑ j 1 c j 1 , j 2 , ⋯ , j t ⋅ X 1 j 1 ) ⋅ X 2 j 2 ⋯ X t j t \begin{aligned} \alpha'(X_1,\cdots,X_t) &= \sum_{j_1,j_2,\cdots,j_t} c_{j_1,j_2,\cdots,j_t}\cdot X_1^{j_1}X_2^{j_2}\cdots X_t^{j_t}\\ &= \sum_{j_2,\cdots,j_t} \left(\sum_{j_1} c_{j_1,j_2,\cdots,j_t}\cdot X_1^{j_1}\right)\cdot X_2^{j_2}\cdots X_t^{j_t} \end{aligned} α′(X1,⋯,Xt)=j1,j2,⋯,jt∑cj1,j2,⋯,jt⋅X1j1X2j2⋯Xtjt=j2,⋯,jt∑(j1∑cj1,j2,⋯,jt⋅X1j1)⋅X2j2⋯Xtjt
其中 j i ∈ [ ϕ ( m i ) ] j_i \in [\phi(m_i)] ji∈[ϕ(mi)](考虑下 ϕ ( m ) \phi(m) ϕ(m) 的分解),因此关于 X 1 X_1 X1 的每个小多项式的长度为 ϕ ( m 1 ) \phi(m_1) ϕ(m1),共有 ϕ ( m ) / ϕ ( m 1 ) \phi(m)/\phi(m_1) ϕ(m)/ϕ(m1) 个小多项式。
[HS15] 采取的编码方式是,将它们的连续 d d d 个系数打包在单个槽内,总共需要 ϕ ( m 1 ) / d \phi(m_1)/d ϕ(m1)/d 个明文槽。恰好我们选择的参数下,包含 ϕ ( m ) / ϕ ( m 1 ) \phi(m)/\phi(m_1) ϕ(m)/ϕ(m1) 条长度为 k 1 = ϕ ( m 1 ) / d k_1=\phi(m_1)/d k1=ϕ(m1)/d 的维度 1 1 1 超列,因此每条维度 1 1 1 的超列都记录一个小多项式。
[HS15] 定义了 Eval 线性变换,它用于多点求值 α ′ ( X 1 , ⋯ , X t ) \alpha'(X_1,\cdots,X_t) α′(X1,⋯,Xt),共分为 t t t 个截断,
-
第 1 1 1 阶段,小多项式 P j 2 , ⋯ , j t ( X 1 ) = ∑ j 1 c j 1 , j 2 , ⋯ , j t ⋅ X 1 j 1 P_{j_2,\cdots,j_t}(X_1) = \sum_{j_1} c_{j_1,j_2,\cdots,j_t}\cdot X_1^{j_1} Pj2,⋯,jt(X1)=∑j1cj1,j2,⋯,jt⋅X1j1 存放在索引 ( ⋆ , j 2 , ⋯ , j t ) (\star,j_2,\cdots,j_t) (⋆,j2,⋯,jt) 的维度 1 1 1 超列,
-
关于多点 ζ 1 g 1 e 1 , 0 ≤ e 1 < k 1 \zeta_1^{g_1^{e_1}},0\le e_1<k_1 ζ1g1e1,0≤e1<k1 的求值可以写作某线性变换 M 1 : Z p r d ⋅ k 1 → E k 1 M_1: \mathbb Z_{p^r}^{d\cdot k_1} \to E^{k_1} M1:Zprd⋅k1→Ek1(多项式的系数表示就是 power basis 下的坐标),可以利用 [HS18] 的 BSGS 技巧
-
计算结果是各个 e 1 e_1 e1 索引的更少变元的若干多项式
A e 1 = α ′ ( ζ 1 g 1 e 1 , X 2 , ⋯ , X t ) A_{e_1} = \alpha'(\zeta_1^{g_1^{e_1}},X_2,\cdots,X_t) Ae1=α′(ζ1g1e1,X2,⋯,Xt)
它的系数存放在索引 ( e 1 , ⋆ , ⋯ , ⋆ ) (e_1,\star,\cdots,\star) (e1,⋆,⋯,⋆) 的子超立方
-
-
第 2 2 2 阶段,我们将 A e 1 A_{e_1} Ae1 继续拆分为关于 X 2 X_2 X2 的小多项式求值,
A e 1 ( X 2 , ⋯ , X t ) = ∑ j 2 , j 3 , ⋯ , j t P j 2 , j 3 , ⋯ , j t ( ζ 1 g 1 e 1 ) ⋅ X 2 j 2 X 3 j 3 ⋯ X t j t = ∑ j 2 , j 3 , ⋯ , j t ( ∑ j 2 P j 2 , j 3 , ⋯ , j t ( ζ 1 g 1 e 1 ) ⋅ X 2 j 2 ) ⋅ X 3 j 3 ⋯ X t j t \begin{aligned} A_{e_1}(X_2,\cdots,X_t) &= \sum_{j_2,j_3,\cdots,j_t} P_{j_2,j_3,\cdots,j_t}(\zeta_1^{g_1^{e_1}})\cdot X_2^{j_2}X_3^{j_3}\cdots X_t^{j_t}\\ &= \sum_{j_2,j_3,\cdots,j_t} \left(\sum_{j_2} P_{j_2,j_3,\cdots,j_t}(\zeta_1^{g_1^{e_1}})\cdot X_2^{j_2}\right)\cdot X_3^{j_3}\cdots X_t^{j_t} \end{aligned} Ae1(X2,⋯,Xt)=j2,j3,⋯,jt∑Pj2,j3,⋯,jt(ζ1g1e1)⋅X2j2X3j3⋯Xtjt=j2,j3,⋯,jt∑(j2∑Pj2,j3,⋯,jt(ζ1g1e1)⋅X2j2)⋅X3j3⋯Xtjt
这些小多项式 Q e 1 , j 3 , ⋯ , j t ( X 2 ) Q_{e_1,j_3,\cdots,j_t}(X_2) Qe1,j3,⋯,jt(X2) 被存放在索引 ( e 1 , ⋆ , j 3 , ⋯ , j t ) (e_1,\star,j_3,\cdots,j_t) (e1,⋆,j3,⋯,jt) 的维度 2 2 2 超列,类似地执行线性变换 M 2 M_2 M2 计算出它们,获得索引 ( e 1 , e 2 , ⋆ , ⋯ , ⋆ ) (e_1,e_2,\star,\cdots,\star) (e1,e2,⋆,⋯,⋆) 的子超立方 -
对于 3 , ⋯ , t 3,\cdots,t 3,⋯,t 阶段,也是类似的
对于 Coeff-to-Slot 过程,就是上述 Eval 变换的逆过程。
由于 digit-extraction 是作用在明文槽基环 Z p e + r \mathbb Z_{p^{e+r}} Zpe+r 上的,因此需要利用 Frobenius map 构造 E E E-线性映射的线性化多项式,将明文槽内的各个 power basis 的系数分解到 d d d 个 “稀疏打包”(明文仅在基环内)的密文。现在可以执行数字提取了,最后还需将 d d d 个密文重新组合为 “密集打包” 的单个密文,从而可执行 Eval 运算。
当然,[HS15] 也参考 [CH18] 给出了 “薄自举”,也就是明文本身就是稀疏打包的,此时可以将比特提取的过程减少为单个密文,效率基本提升了 d d d 倍(线性变换很快,主要是比特提取)。
Parameters for Recryption
在使用 HElib 时,需要设置合适的参数,使之支持自举程序。然而它并没有提供参数生成的程序。参数集应当满足的条件是:设置特征 p p p 和明文槽长度 n n n
- m m m 和 p p p 互素,从而 p p p 是 Z m ∗ \mathbb Z_m^* Zm∗ 中的元素
- p p p 模 m m m 的乘法阶 d d d 被 n n n 整除,从而 E E E 中存在维度 n n n 的子环
- m m m 被分解为素数幂 m 1 , ⋯ , m t m_1,\cdots,m_t m1,⋯,mt,存在某个 m i ∗ m_{i^*} mi∗ 使得 p p p 模 m i ∗ m_{i^*} mi∗ 的乘法阶也是 d d d,从而 Z m ∗ / ( p ) \mathbb Z_m^*/(p) Zm∗/(p) 的阶是 k = ϕ ( m ) / d k=\phi(m)/d k=ϕ(m)/d
- 重排使得 m i ∗ m_{i^*} mi∗ 成为 m 1 m_1 m1,使得 Z m 1 ∗ / ( p ) \mathbb Z_{m_1}^*/(p) Zm1∗/(p) 是循环群,计算生成元 g ˉ 1 \bar g_1 gˉ1 和阶 l 1 l_1 l1,然后用 CRT 提升为 Z m ∗ \mathbb Z_m^* Zm∗ 的生成元 g 1 g_1 g1
- 对于 i > 1 i>1 i>1,继续让 Z m i ∗ / ( p d ) \mathbb Z_{m_i}^*/(p^d) Zmi∗/(pd) 是循环群,计算生成元 g ˉ i \bar g_i gˉi 和阶 l i l_i li,然后用 CRT 提升为 Z m ∗ \mathbb Z_m^* Zm∗ 的生成元 g i g_i gi
- 事实上 p d ( m o d m i ) = 1 p^d \pmod{m_i}=1 pd(modmi)=1,因此 g i , ∀ i > 2 g_i, \forall i>2 gi,∀i>2 在模 m m m 下的阶就等于在模 m i m_i mi 下的阶(good dimension),从而超立方的一维旋转是高效的
HElib要求将 o r d ( g i m o d m i ) = o r d ( g i m o d m ) ord(g_i \bmod m_i)=ord(g_i \bmod m) ord(gimodmi)=ord(gimodm) 的排在最前面,因此将上述结果反序
[HS15] 测试了一些参数下的性能,
- “thick” 版本的自举:用于稠密打包的明文,耗时较多。

- “thin” 版本的自举:专用于稀疏打包的明文,计算效率提高了大约 d d d 倍。它需要先执行 Slot-to-Coeff 变换(Froward-DFT),因此要求 min capacity 剩余;在末尾不执行它,因此 after capacity 也相对更大。

CH18
[HS15] 的比特提取程序的复杂度严重依赖明文模数 p r p^r pr 的规模,对于较大的明文规模速度很慢。[CH18] 提出了更适合较大明文模数的自举算法,并给出 BFV 的第一个自举实现。此外,[CH18] 提出了 “瘦模式” 的自举,也就是 HElib 中的 “薄自举”。
Digit Removal Algorithm
[HS15] 采用 lifting polynomials 在 LSD 高位依次插入零,而 [CH18] 使用 lowest digit removal polynomials 直接计算出 LSD
简记 u i , j u_{i,j} ui,j 表示 u [ i ] + ( p i + j + 1 ) u[i]+(p^{i+j+1}) u[i]+(pi+j+1) 等价类,或者说 u [ i ] ( m o d p i + j + 1 ) u[i]\pmod{p^{i+j+1}} u[i](modpi+j+1)

在 [GHS12] 和 [HS15] 的比特提取程序中,利用 F e ( X ) F_e(X) Fe(X) 从 u i , 0 u_{i,0} ui,0(绿色数字)迭代计算出 u i , e − i − 1 u_{i,e-i-1} ui,e−i−1(同一行的蓝色数字),然后从 u u u 中减去 u k , i + 1 − k ⋅ p k , k ≤ i u_{k,i+1-k}\cdot p^{k},k\le i uk,i+1−k⋅pk,k≤i(所在的反对角线)获得 u i + 1 , 0 u_{i+1,0} ui+1,0(下一行的绿色数字)。
在上述运算中, u 0 , e − 1 = F e e − 1 ( u 0 , 0 ) u_{0,e-1}=F_e^{e-1}(u_{0,0}) u0,e−1=Fee−1(u0,0),由于 F e ( X ) F_e(X) Fe(X) 本身就是 p p p 次多项式,因此计算 u 0 , e − 1 u_{0,e-1} u0,e−1 的多项式度数是 p e − 1 p^{e-1} pe−1,需要的乘法深度较大(度数更大,乘法数量不一定多,但是乘法深度一定大)。
[CH18] 指出:对于任意素数 p p p 和指数 e ≥ 1 e \ge 1 e≥1,从存在度数至多 ( e − 1 ) ( p − 1 ) + 1 (e-1)(p-1)+1 (e−1)(p−1)+1 的多项式 f ( x ) f(x) f(x),它将整数 0 ≤ x < p e 0 \le x < p^e 0≤x<pe 映射为
f ( x ) ≡ x − [ x ] p ( m o d p e ) f(x) \equiv x-[x]_p \pmod{p^e} f(x)≡x−[x]p(modpe)
它可以直接移除 LSD(不过它无法移除其他的 digits,因此依旧需要和 lifting polynomials 组合使用),从而 g ( x ) : = x − f ( x ) g(x):=x-f(x) g(x):=x−f(x) 就是提取 LSB 的度数至多 ( e − 1 ) ( p − 1 ) + 1 (e-1)(p-1)+1 (e−1)(p−1)+1 的多项式。
这个多项式的具体构造:首先定义如下的函数,
F A ( x ) : = ∑ j = 0 ∞ ( − 1 ) j ( A + j − 1 j ) ( x A + j ) F_A(x) := \sum_{j=0}^\infty (-1)^j {A+j-1 \choose j}{x \choose A+j} FA(x):=j=0∑∞(−1)j(jA+j−1)(A+jx)
它的功能是将 M ≥ A M\ge A M≥A 映射到 F A ( M ) = 1 F_A(M)=1 FA(M)=1,其余的是 F A ( M ) = 0 F_A(M)=0 FA(M)=0(一个输入固定为 A A A 的比较函数)
我们继续定义如下函数,其中的系数 a ( m ) a(m) a(m) 是 F p , F 2 p , ⋯ F_{p},F_{2p},\cdots Fp,F2p,⋯ 的 x m x^m xm 系数累加,
f ^ ( x ) = p ∑ j = 1 ∞ F j p ( x ) = ∑ m = p ∞ a ( m ) ( x m ) \hat f(x) = p\sum_{j=1}^\infty F_{jp}(x) = \sum_{m=p}^\infty a(m){x \choose m} f^(x)=pj=1∑∞Fjp(x)=m=p∑∞a(m)(mx)
它的功能是计算 max k { x ≥ k p } \max_k\{x\ge kp\} maxk{x≥kp} 或者说 x − [ x ] p x-[x]_p x−[x]p
我们实际只需要 x − [ x ] p ( m o d p e ) x-[x]_p \pmod{p^e} x−[x]p(modpe) 等价类,而非 x − [ x ] p ∈ Z x-[x]_p \in \mathbb Z x−[x]p∈Z 本身,因此只需要它的有限截断(更高的那些 x m x^m xm 不再影响 u [ e − 1 : 0 ] u[e-1:0] u[e−1:0] 内的数据):
f ( x ) = ∑ m = p ( e − 1 ) ( p − 1 ) + 1 a ( m ) ( x m ) f(x) = \sum_{m=p}^{(e-1)(p-1)+1} a(m){x \choose m} f(x)=m=p∑(e−1)(p−1)+1a(m)(mx)
利用上述构造的 f ( x ) , g ( x ) f(x),g(x) f(x),g(x),假定我们想要移除最低的 v v v 个数位,那么需要计算出 u [ 0 ] ( m o d p e ) , u [ 1 ] ( m o d p e − 1 ) , ⋯ , u [ v − 1 ] ( m o d p e − v ) u[0] \pmod{p^e},u[1]\pmod{p^{e-1}},\cdots,u[v-1]\pmod{p^{e-v}} u[0](modpe),u[1](modpe−1),⋯,u[v−1](modpe−v),计算过程为:根据 u i , 0 u_{i,0} ui,0(绿色数字)直接计算 g ( x ) g(x) g(x) 获得 u i , e − i − 1 u_{i,e-i-1} ui,e−i−1(红色数字),还需迭代计算 F e F_e Fe 获得 u i , v − i − 1 u_{i,v-i-1} ui,v−i−1(同一行的蓝色数字)用于获取 u i + 1 , 0 u_{i+1,0} ui+1,0(下一行的绿色数字)。

复杂度分析:
- 为了计算 u i , 0 u_{i,0} ui,0,需要 u u u 减去反对角线上的那些数字, u 0 , i = F e i ( u ) u_{0,i}=F_e^i(u) u0,i=Fei(u) 的次数为 p i p^i pi, , u 1 , i − 1 = F e i − 1 ( u 1 , 0 ) , u_{1,i-1}=F_e^{i-1}(u_{1,0}) ,u1,i−1=Fei−1(u1,0) 的次数也是 p i p^i pi,其他的也都是,因此计算 u i , 0 u_{i,0} ui,0 的多项式次数为 p i p^i pi
- 在 [HS15] 方法中,计算 u i , e − i − 1 u_{i,e-i-1} ui,e−i−1 需要计算 F e e − i − 1 ( u i , 0 ) F_e^{e-i-1}(u_{i,0}) Fee−i−1(ui,0),它自身的次数为 p e − i − 1 p^{e-i-1} pe−i−1,总的度数为 p e − 1 p^{e-1} pe−1
- 在 [CH18] 方法中,计算 u i , e − i − 1 u_{i,e-i-1} ui,e−i−1 需要计算 g ( u i , 0 ) g(u_{i,0}) g(ui,0),它自身的次数仅为 ( p − 1 ) ( e − i − 1 ) + 1 (p-1)(e-i-1)+1 (p−1)(e−i−1)+1,总的度数为 e p v ep^{v} epv
- 当 v ≤ e − 1 v \le e-1 v≤e−1 并且 p > e p>e p>e 时(较大的明文模数),[CH18] 的方法复杂度更低
不过,后续的 [GV23] 给出了 BGV/GFV 的统一自举算法,指出两者的自举复杂度是完全相同的。
如果计算某些蓝色数字时,满足了条件 p l > ( p − 1 ) ( e − i − 1 ) + 1 p^l>(p-1)(e-i-1)+1 pl>(p−1)(e−i−1)+1,那么可以直接使用红色数字(比同一行的蓝色数字含有更多的高位零,因此必定是正确的)来构造下一行的绿色数字,多项式的度数会更低。[CH18] 的数位移除程序为:

Bootstrapping for FV and BGV
对于 BGV 自举:
- 密文模数需要和明文特征互素,选取 q = p e + 1 q=p^e+1 q=pe+1
- 相位 [ p r v + m ] q [p^rv+m]_{q} [prv+m]q,
- 明文放大 p p p 倍:计算 c t ⋅ [ p ] q ct \cdot [p]_q ct⋅[p]q,相位变为 [ p r + 1 v + p m ] q [p^{r+1}v+pm]_{q} [pr+1v+pm]q
- 明文缩小 p p p 倍(要求 p ∣ m p \mid m p∣m):计算 c t ⋅ [ p − 1 ] q ct \cdot [p^{-1}]_q ct⋅[p−1]q,相位变为 [ p r − 1 v + m / p ] q [p^{r-1}v+m/p]_{q} [pr−1v+m/p]q
对于 BFV 自举:
- 密文模数和明文特征之间没有要求,选取 q = p e q=p^e q=pe
- 相位 [ p e − r m + v ] q [p^{e-r}m+v]_q [pe−rm+v]q,
- 明文放大 p p p 倍:将 Δ = p e − r \Delta=p^{e-r} Δ=pe−r 修改为 Δ ′ = p e − r − 1 \Delta'=p^{e-r-1} Δ′=pe−r−1,相位依旧是 [ p e − r − 1 ⋅ p m + v ] q [p^{e-r-1}\cdot pm+v]_q [pe−r−1⋅pm+v]q
- 明文缩小 p p p 倍(要求 p ∣ m p \mid m p∣m):将 Δ = p e − r \Delta=p^{e-r} Δ=pe−r 修改为 Δ ′ = p e − r + 1 \Delta'=p^{e-r+1} Δ′=pe−r+1,相位依旧是 [ p r − 1 + 1 ⋅ m / p + v ] q [p^{r-1+1}\cdot m/p + v]_{q} [pr−1+1⋅m/p+v]q
采取 [HS15] 对 BGV 自举的框架,[CH18] 对于 BFV 自举的框架为:

此外,[CH18] 对于 “稀疏打包” 的明文,提出了 “slim mode” 版本的自举。需要注意的是,它首先在待自举的密文上执行 Slot-to-Coeff 线性变换,因此要求输入密文的 Level 不能被消耗殆尽,必须能够支撑这个线性变换。当然,它的数字提取之后不必执行 Slot-to-Coeff 变换,因此输出密文的 Level 也会稍大一点。

在附录部分,[CH18] 对于 m m m 是二的幂次的特殊情况,给出了更加高效的迭代线性变换算法(类似 FFT/NTT)。不过同态线性变换的开销相对于数字提取来说是较小的,影响不算大。
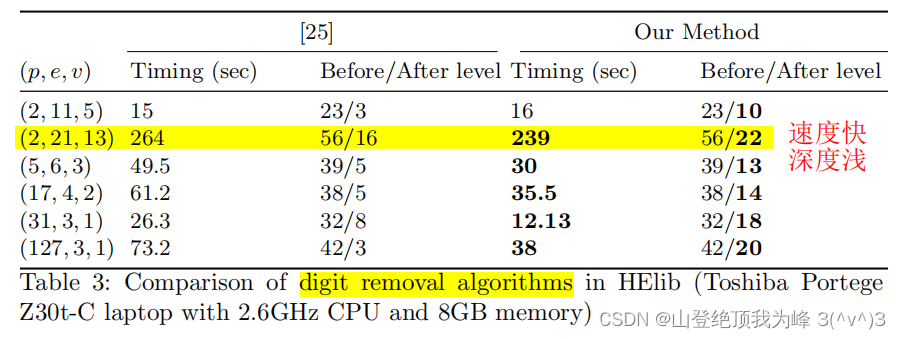
效率对比:对于 e ≥ v + 2 e \ge v+2 e≥v+2 以及较大的 p p p,[CH18] 的方法更好,
相关文章:

Bit Extraction and Bootstrapping for BGV/BFV
参考文献: [GHS12] Gentry C, Halevi S, Smart N P. Better bootstrapping in fully homomorphic encryption[C]//International Workshop on Public Key Cryptography. Berlin, Heidelberg: Springer Berlin Heidelberg, 2012: 1-16.[AP13] Alperin-Sheriff J, Pe…...
七八分钟快速用k8s部署springboot前后端分离项目
前置依赖 k8s集群,如果没有安装,请先安装 kubectl ,客户端部署需要依赖 应用镜像构建 应用镜像构建不用自己去执行,相关镜像已经推送到docker hub 仓库,如果要了解过程和细节,可以看一下,否…...
软件技术有限公司面试问题与解答(2)—— Linux内核内存初始化的完整流程1)
中移(苏州)软件技术有限公司面试问题与解答(2)—— Linux内核内存初始化的完整流程1
接前一篇文章:中移(苏州)软件技术有限公司面试问题与解答(1)—— 可信计算国密标准 本文参考以下文章: 启动期间的内存管理之初始化过程概述----Linux内存管理(九) Linux初始化 特此致谢! 本…...

蓝桥杯、编程考级、NOC、全国青少年信息素养大赛—scratch列表考点
1、小小情报员(202309scratch四级24题) 1.准备工作 (1)选择背景 Colorful City; (2)保留角色小猫,选择角色Ballerina。 2.功能实现 (1)角色小猫初始位置…...

1.23 力扣图论
841. 钥匙和房间 有 n 个房间,房间按从 0 到 n - 1 编号。最初,除 0 号房间外的其余所有房间都被锁住。你的目标是进入所有的房间。然而,你不能在没有获得钥匙的时候进入锁住的房间。 当你进入一个房间,你可能会在里面找到一套不…...

Vue学习笔记9--vuex(专门在Vue中实现集中式状态(数据)管理的一个Vue插件)
一、vuex是什么? 概念:专门在Vue中实现集中式状态(数据)管理的一个Vue插件,对vue应用中多个组件的共享状态进行集中式的管理(读/写),也是一种组件间通信的方式,且适用于…...
Operation
contents 服务器一、相关概念1.1 云服务器与实例1.2 关于域名解析延时与80端口1.3 关于备案1.4 关于SSL证书1.5 关于SSL证书的签发1.6 关于SSL证书的部署1.7 关于LNMP和LAMP1.8 关于bt面板 二、单服务器单一级域名多网站2.1 创建多个二级域名2.2 解析二级域名绑定到服务器上2.3…...
)
Kong关键概念 - 服务(Services)
服务(Services) 在Kong Gateway中,服务是代表外部上游(upstream)API或微服务的实体。例如,数据转换微服务、计费API等。 服务的主要属性是其URL。您可以使用一个字符串来指定URL,或者通过分别…...

IDEA更改页面不重启
IDEA更改页面不重启 idea若依 修改包名 idea 1、修改IDEA设置 File -> Settings -> Build Execution Deployment -> Build Project automatically 勾选2、勾选Running Ctrl Shift Alt / 然后选择 Registry,勾上 Compiler.autoMake.allow.when.app.runn…...

golang学习-channel管道
1、定义 管道是golang语言提供的goroutine间的通讯方式,channel可以让一个goroutine发送特定的值给另一个goroutine的通讯机制。 管道是引用类型。 golang语言中channel是一种特殊的类型。像一个队列一样,先进先出。 var 变量 chan 元素类型 var ch1 …...

oracle 12 查询数据库锁
在Oracle 12c中,查询数据库锁信息可以通过以下视图进行: v$locked_object:这个视图显示了当前被锁定的对象(如表、行等)的信息。 SELECT l.session_id sid, s.serial#, l.locked_mode,o.object_name,s.osuser,s.userna…...

【LeetCode-135】分发糖果(贪心)
LeetCode135.分发糖果 题目描述 老师想给孩子们分发糖果,有 N 个孩子站成了一条直线,老师会根据每个孩子的表现,预先给他们评分。 你需要按照以下要求,帮助老师给这些孩子分发糖果: 每个孩子至少分配到 1 个糖果。…...
5G_射频测试_发射机测量(四)
6.2 Base station output power 用于测量载波发射功率的大小,功率越大小区半径越大但是杂散也会越大 载波功率(用频谱仪测)天线口功率(用功率计测)载波功率是以RBW为单位的filter测量的积分功率不同带宽的多载波测试时…...

MySQL经典50题
目录 一、数据表介绍 二、练习题 1. 查询" 01 "课程比" 02 "课程成绩高的学生的信息及课程分数 2. 查询同时存在" 01 "课程和" 02 "课程的情况 3. 查询存在" 01 "课程但可能不存在" 02 "课程的情况…...

常用的Qt开源库分享
1. Qwt (https://qwt.sf.net): Qwt是一个基于Qt的数据可视化库,提供了绘制曲线、图表、仪表盘等功能。 2. QJson (https://qjson.sourceforge.net): QJson是一个用于JSON数据解析和生成的库,使Qt应用程序能够方便地处理JSON格式的数据。 3. QCustomP…...

Unity开发授权系统
Unity开发授权系统 引子 因为有些客户尾款到账不及时,因此研究了一套授权系统,当授权到期后,系统就提示软件授权已到期,不能继续使用云云,这样方便尾款的收回。 大体需求就是 时间相关性,可以自由设置授…...

一周时间,开发了一款封面图生成工具
介绍 这是一款封面图的制作工具,根据简单的配置即可生成一张好看的封面图,目前已有七款主题可以选择。做这个工具的初衷来自平时写文章,都为封面图发愁,去图片 网站上搜索很难找到满意的,而且当你要的图如果要搭配上文…...

【.NET Core】深入理解异步编程模型(APM)
【.NET Core】深入理解异步编程模型(APM) 文章目录 【.NET Core】深入理解异步编程模型(APM)一、APM概述二、IAsyncResult接口2.1 BeginInvoke2.2 EndInvoke2.3 IAsyncResult属性2.4 IAsyncResult异步演示 三、通过结束异步操作来…...

pyqtgraph绘图类
pyqtgraph绘图类 pyqtgraph绘图有四种方法: 方法描述pyqtgraph.plot()创建一个新的QWindow用来绘制数据PlotWidget.plot()在已存在的QWidget上绘制数据PlotItem.plot()在已存在的QWidget上绘制数据GraphicsLayout.addPlot()在网格布局中添加一个绘图 上面四个方法都接收同样…...

C#6-10新增的内容
目录 异常筛选器 属性语法 表达式主体定义 Null 条件运算符 ?. 和 ?[] 使用 $ 的字符串内插 nameof 表达式 元组类型 模糊匹配 本地函数 Expression-bodied 成员 Reference 变量 ?、??和??= .. 模式匹配功能(C# 9) Record init c#8.NET Framework 4.8…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

leetcode73-矩阵置零
leetcode 73 思路 记录 0 元素的位置:遍历整个矩阵,找出所有值为 0 的元素,并将它们的坐标记录在数组zeroPosition中置零操作:遍历记录的所有 0 元素位置,将每个位置对应的行和列的所有元素置为 0 具体步骤 初始化…...

Java中栈的多种实现类详解
Java中栈的多种实现类详解:Stack、LinkedList与ArrayDeque全方位对比 前言一、Stack类——Java最早的栈实现1.1 Stack类简介1.2 常用方法1.3 优缺点分析 二、LinkedList类——灵活的双端链表2.1 LinkedList类简介2.2 常用方法2.3 优缺点分析 三、ArrayDeque类——高…...
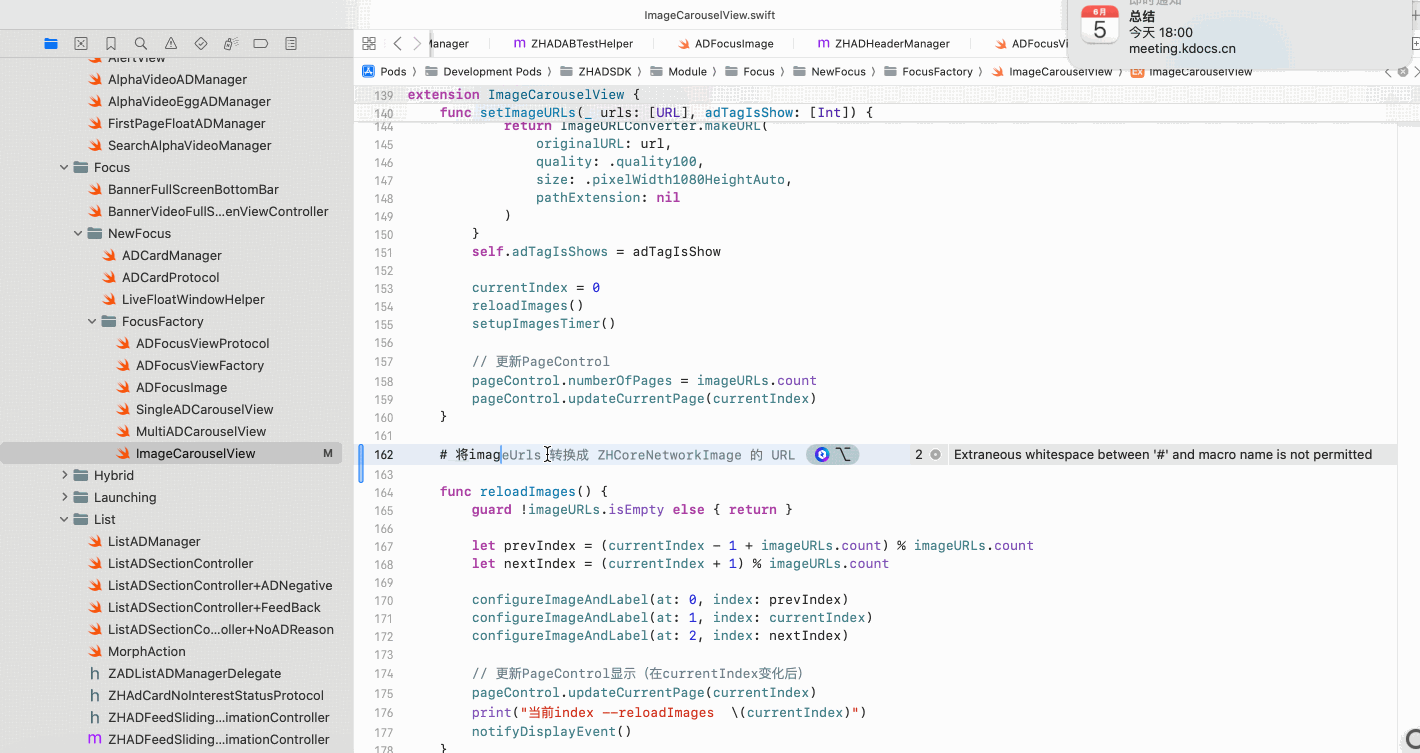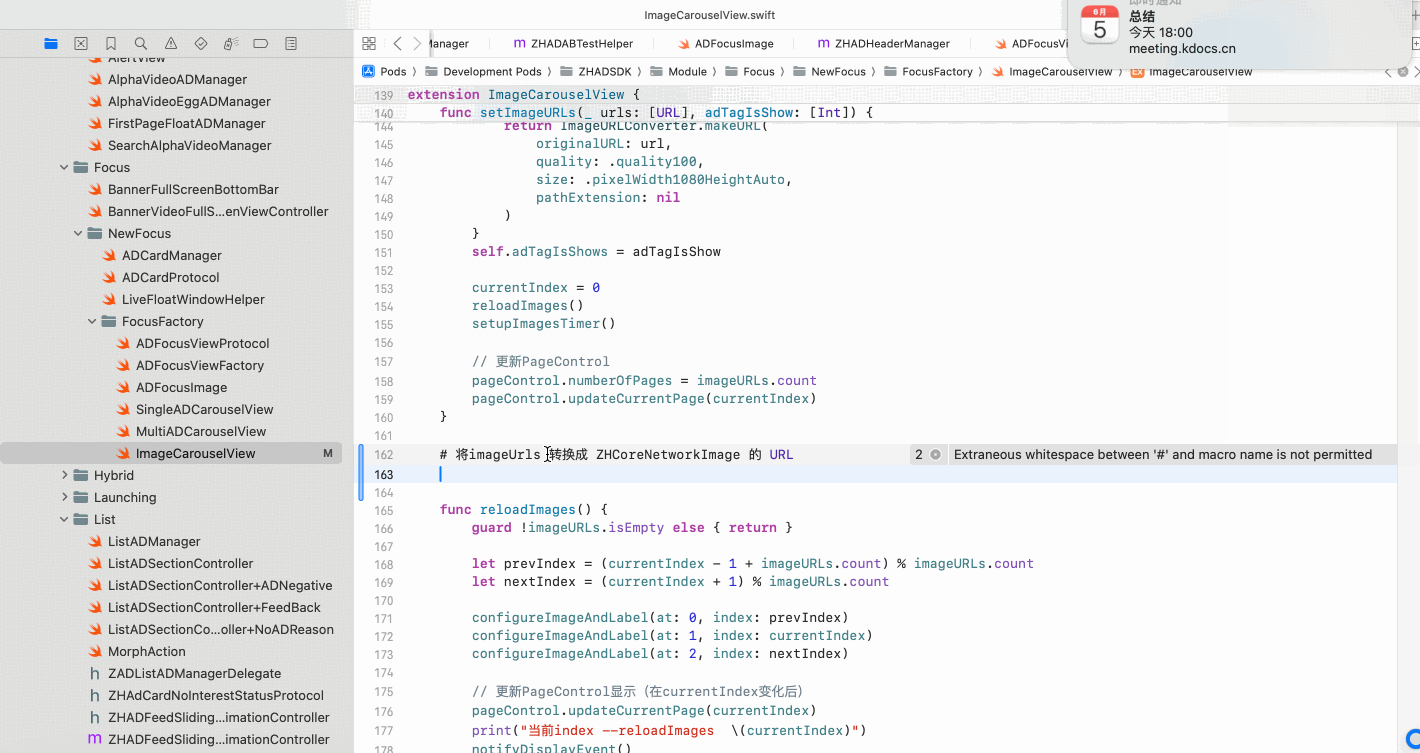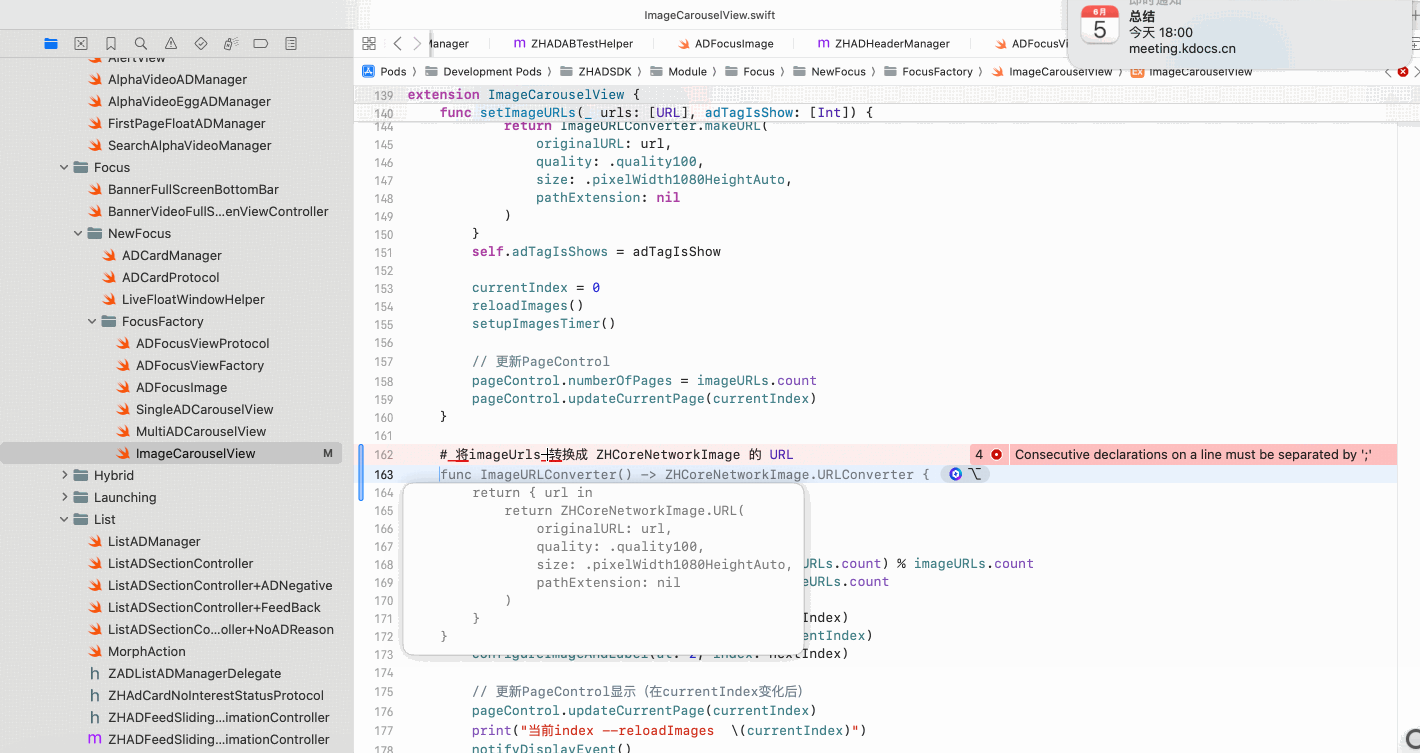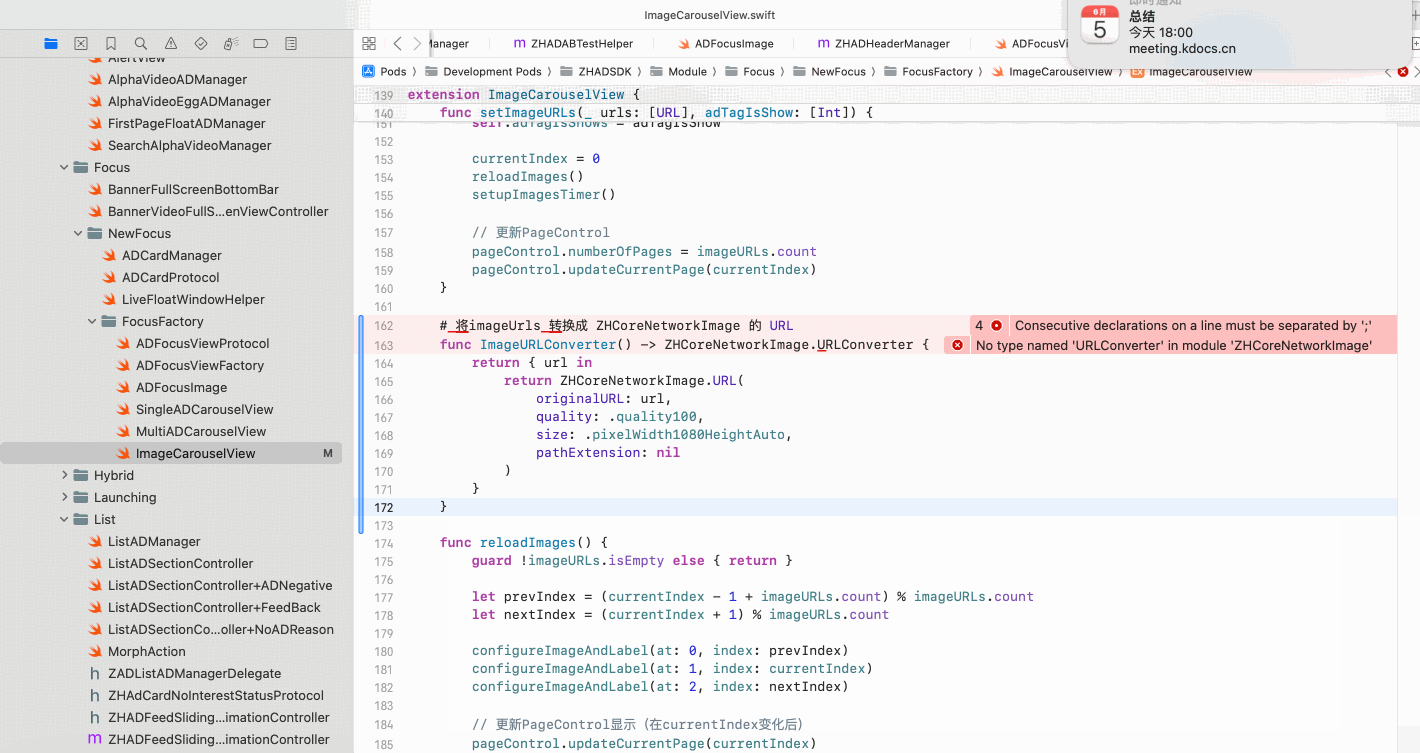
Copilot for Xcode (iOS的 AI辅助编程)
Copilot for Xcode 简介Copilot下载与安装 体验环境要求下载最新的安装包安装登录系统权限设置 AI辅助编程生成注释代码补全简单需求代码生成辅助编程行间代码生成注释联想 代码生成 总结 简介 尝试使用了Copilot,它能根据上下文补全代码,快速生成常用…...

接口 RESTful 中的超媒体:REST 架构的灵魂驱动
在 RESTful 架构中,** 超媒体(Hypermedia)** 是一个核心概念,它体现了 REST 的 “表述性状态转移(Representational State Transfer)” 的本质,也是区分 “真 RESTful API” 与 “伪 RESTful AP…...

中国政务数据安全建设细化及市场需求分析
(基于新《政务数据共享条例》及相关法规) 一、引言 近年来,中国政府高度重视数字政府建设和数据要素市场化配置改革。《政务数据共享条例》(以下简称“《共享条例》”)的发布,与《中华人民共和国数据安全法》(以下简称“《数据安全法》”)、《中华人民共和国个人信息…...
