数据结构<1>——树状数组
树状数组,也叫Fenwick Tree和BIT(Binary Indexed Tree),是一种支持单点修改和区间查询的,代码量小的数据结构。
那神马是单点修改和区间查询?我们来看一道题。
洛谷P3374(模板): 在本题中,单点修改就是将某一个数加上x的操作,区间查询就是求出某区间每一个数的和的操作,这下明白了吧。
下面来解释一下树状数组的工作原理。先看一张图(来源于OI-Wiki)
Tips:别找了,点一下"图"那个字就有了。
我们发现,树状数组总能将一段前缀拆成不多于段区间,使得这几段区间的信息是已知的。因此,我们只用合并这些区间的信息,就可以得到答案。因此,时间复杂度从
变成
,效率大大提高。
管辖区间
我们观察刚刚的图发现,每个相当于一个小leader,掌管自己的范围。那这个范围是多少呢?我们规定
管辖的区间长度为
,其中k为x的二进制表示中,最低位的1所在的二进制位数。而
为x的二进制表示中,最低位的1以及后面所有0组成的数。即
管辖的区间是
。注意:lowbit(x)表示这个1和后面所有0组成的
。
下面附上OI-Wiki中对lowbit(x)的原理的解释(其实是我不会解释)
将 x 的二进制所有位全部取反,再加 1,就可以得到 -x 的二进制编码。例如,![]() 的二进制编码是
的二进制编码是 110,全部取反后得到 001,加 1 得到 010。
设原先 x 的二进制编码是 (...)10...00,全部取反后得到 [...]01...11,加 1 后得到 [...]10...00,也就是 -x 的二进制编码了。这里 x 二进制表示中第一个 1 是 x 最低位的 1。
(...) 和 [...] 中省略号的每一位分别相反,所以 x & -x = (...)10...00 & [...]10...00 = 10...00,得到的结果就是 lowbit。
//lowbit的实现
int lowbit(int x){return x&(-x);
}lowbit可以说是一个很经典的二进制运算了。
区间查询
经过上面的分析,我们可以知道回答区间查询的步骤了:
· 从往前跳,一直让
就行了。
· 如果x=0就结束循环
· 将跑到的累加
实现如下↓:
int get_sum(int x){int sum=0;while(x>0){sum+=c[x];x-=lowbit(x);}return sum;
}单点修改
也很简单。
· 先修改
· 然后一直让让
· 如果x=n就结束循环
实现如下↓:
void modify(int x,int y){while(x<=n){c[x]+=y;x+=lowbit(x);}
}洛谷P3374(模板):
那这题就很easy啦~
#include <bits/stdc++.h>
using namespace std;
int c[maxn];
int n,m;
int lowbit(int x){return x&(-x);
}
void modify(int x,int y){while(x<=n){c[x]+=y;x+=lowbit(x);}
}
int get_sum(int x){int res=0;while(x>0){res+=c[x];x-=lowbit(x);}return res;
}
int main(){cin>>n>>m;for(int i=1;i<=n;i++){int x;cin>>x;modify(i,x);}for(int i=1;i<=m;i++){int op,x,y;cin>>op>>x>>y;if(op==1)modify(x,y);if(op==2)cout<<get_sum(y)-get_sum(x-1)<<endl;}return 0;
}别走啊,这不得在找几题练练?
逆序对:
基础题。现在按照序列从左到右将数据的值对应的位置的数加一,代表又有一个数出现。因此,在循环到第i项时,前i-1项已经加入到树状数组内了,树状数组内比大的都会与
构成逆序对,因为它们一定出现的更早,所以产生的逆序对数量为
。要注意的是,我们需要进行离散化,因为根据
建树确实不够。然后就是代码部分啦。
#include <bits/stdc++.h>
using namespace std;
pair<long long,long long> a[maxn];
long long b[maxn],c[maxn];
int n;
int lowbit(int x){return x&(-x);
}
void modify(int x){while(x<=n){c[x]++;x+=lowbit(x);}
}
int get_sum(int x){int sum=0;while(x>0){sum+=c[x];x-=lowbit(x);}return sum;
}
int main(){cin>>n;for(int i=1;i<=n;i++){cin>>a[i].first;a[i].second=i;}sort(a+1,a+n+1);for(int i=1;i<=n;i++)b[a[i].second]=i;long long ans=0;for(int i=n;i;i--){ans+=get_sum(b[i]);modify(b[i]);}cout<<ans<<endl;return 0;
}当然,用归并也是Ok的。
火柴排队:
一道非常非常经典的题目。我们乍一看,就是让我们最小化,也就是最小化
,也就是a序列第k大的元素必须和序列b中第k大的元素
的位置必须一样。OK,那我们把a,b离散化,问题变成了b序列要交换几次可以令其等于a。我们令
,相当于以
为关键字对序列
排序,如果a和b一样,那么
。那么我们需要让q升序排列。问题又变成,将原本乱的 q序列升序排列的最少交换次数。
诶,这不就是逆序对吗?
用树状数组或归并即可。这里给归并的代码,树状数组的参考上面P1908的代码。
#include <bits/stdc++.h>
using namespace std;
int a[maxn],b[maxn];
int c[maxn],d[maxn];
int num1[maxn],num2[maxn];
int calc[maxn];
long long ans=0;
int tmp[maxn];
void msort(int l,int r){if(l==r)return;int mid=(l+r)>>1;msort(l,mid);msort(mid+1,r);int i=l,j=mid+1;int k=l;while(i<=mid && j<=r){if(a[i]<=a[j])tmp[k++]=a[i++];else{tmp[k++]=a[j++];ans+=mid-i+1;ans%=MOD;}}while(i<=mid)tmp[k++]=a[i++];while(j<=r)tmp[k++]=a[j++];for(int i=l;i<=r;i++)a[i]=tmp[i];
}
int main(){int n;cin>>n;for(int i=1;i<=n;i++){cin>>a[i];c[i]=a[i];}for(int i=1;i<=n;i++){cin>>b[i];d[i]=b[i];}sort(d+1,d+n+1);for(int i=1;i<=n;i++)num1[d[i]]=i;sort(c+1,c+n+1);for(int i=1;i<=n;i++)num2[c[i]]=i;for(int i=1;i<=n;i++)calc[num1[b[i]]]=i;for(int i=1;i<=n;i++)a[i]=calc[num2[a[i]]];msort(1,n);cout<<ans%MOD<<endl;return 0;
}别忘了取模哦。
The Last Problem:ABC157E
此题一看就是树状数组。但是由于有26个字母,我们要建26个树状数组,每一个存放该字母出现的位置。这样,在询问的时候,直接查询每一个树状数组的[l,r]的和,如果这个和>0,那么就把 ans加1,最后输出即可。
#include <bits/stdc++.h>
using namespace std;
int c[26][500005];
int lowbit(int x){return x&(-x);
}
void update(int c[],int x,int val){while(x<=500000){c[x]+=val;x+=lowbit(x);}
}
int getsum(int c[],int x){int sum=0;while(x>0){sum+=c[x];x-=lowbit(x);}return sum;
}
int main(){int n;cin>>n;string str;cin>>str;str=' '+str;for(int i=1;i<=n;i++)update(c[str[i]-'a'],i,1);int q;cin>>q;while(q--){int op;cin>>op;if(op==1){int x;char ch;cin>>x>>ch;update(c[str[x]-'a'],x,-1);update(c[ch-'a'],x,1);str[x]=ch;}if(op==2){int l,r;cin>>l>>r;int ans=0;for(int i=0;i<26;i++){if(getsum(c[i],r)-getsum(c[i],l-1))ans++;}cout<<ans<<endl;}}return 0;
}Ok,以上就是本期的全部内容了。我们下期再见!
温馨提示:本期的所有代码都有问题,请不要无脑Ctrl C+Ctrl V(你会挂的很惨),看懂了自己写一遍
相关文章:
数据结构<1>——树状数组
树状数组,也叫Fenwick Tree和BIT(Binary Indexed Tree),是一种支持单点修改和区间查询的,代码量小的数据结构。 那神马是单点修改和区间查询?我们来看一道题。 洛谷P3374(模板): 在本题中,单点修改就是将某一个数加上…...
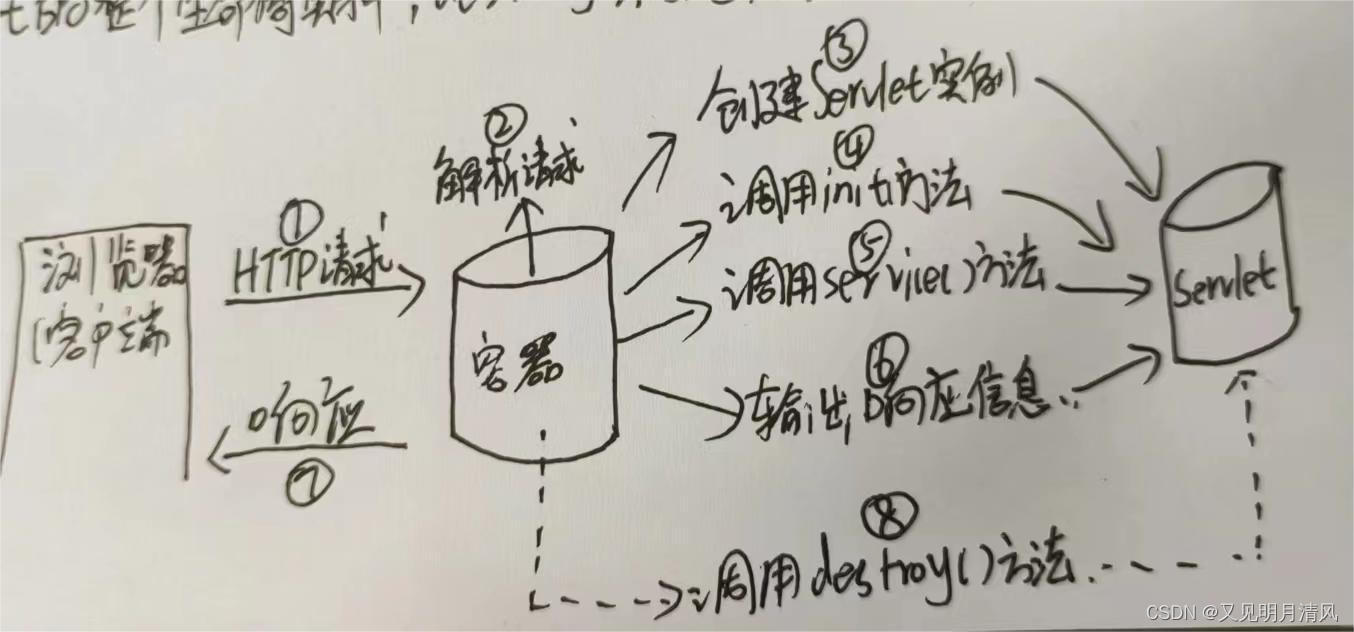
Servlet生命周期
第一阶段: init()初始化阶段 当客户端想Servlet容器(例如Tomcat)发出HTTP请求要求访问Servlet时,Servlet容器首先会解析请求,检查内存中是否已经有了该Servlet对象,如果有ÿ…...
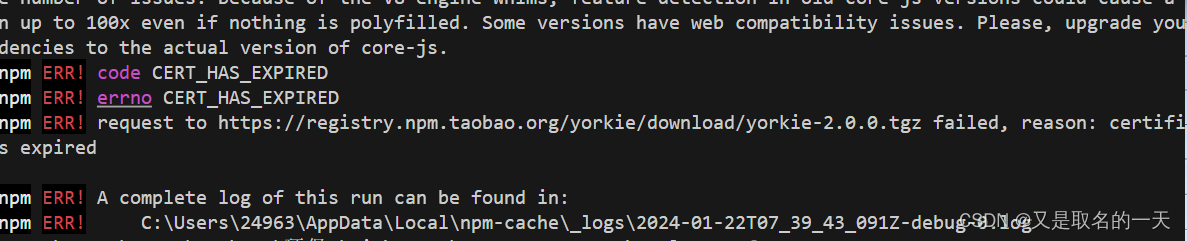
npm i 报一堆版本问题
1,先npm cache clean --force 再下载 插件后缀加上 --legacy-peer-deps 2, npm ERR! code CERT_HAS_EXPIRED npm ERR! errno CERT_HAS_EXPIRED npm ERR! request to https://registry.npm.taobao.org/yorkie/download/yorkie-2.0.0.tgz failed, reason…...

Linux设备管理模型-01:基础数据结构
文章目录 1. 设备管理模型2. 基本数据结构2.1 kobject2.2 kset 1. 设备管理模型 设备模型是内核提供的一个编写驱动的架构。 设备管理是设备-总线-驱动结构。 linux中的设备是由树状模型组织的,从sysfs中可以查看树状结构。 他本身实现了: 电源管理热…...
opencv#32 可分离滤波
滤波的可分离性 就是将一个线性滤波变成多个线性滤波,这里面具体所指的是变成x方向的线性滤波和y方向的线性滤波。无论先做x方向的滤波还是y方向滤波,两者的叠加结果是一致的,这个性质取决于滤波操作是并行的,也就是每一个图像在滤…...

android 导航app 稳定性问题总结
一 重写全局异常处理: 1 是过滤掉一些已知的无法处理的 问题,比如TimeoutException 这种无法根除只能缓解的问题可以直接catch掉 2 是 一些无法继续的问题可以直接杀死重启,一些影响不是很大的,可以局部还原 比如: p…...
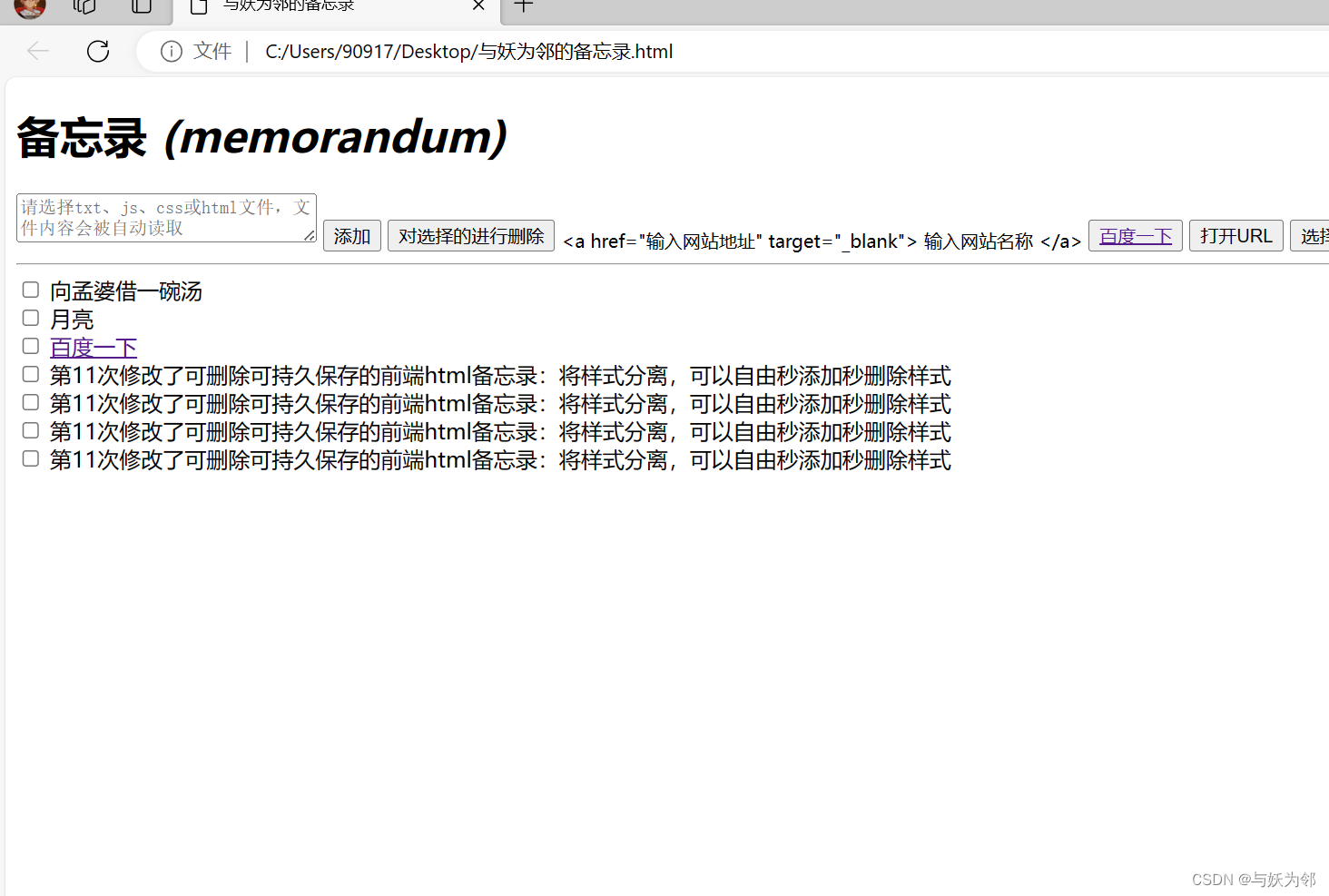
第11次修改了可删除可持久保存的前端html备忘录:将样式分离,可以自由秒添加秒删除样式
第11次修改了可删除可持久保存的前端html备忘录:将样式分离,可以自由秒添加秒删除样式 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport" content"…...
hcip高级网络知识
一:计算机间信息传递原理 抽象语言----编码 编码---二进制 二进制---转换为电流(数字信号) 处理和传递数字信号 二:OSI--七层参考模型 ISO--1979 规定计算机系统互联的组织: OSI/RM ---- 开放式系统互联参考模型 --- 1…...
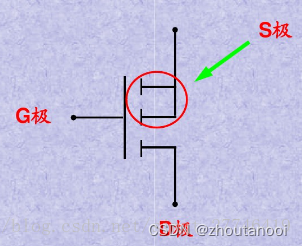
常用电子器件学习——MOS管
MOS管介绍 MOS,是MOSFET的缩写。MOSFET 金属-氧化物半导体场效应晶体管,简称金氧半场效晶体管(Metal-Oxide-Semiconductor Field-Effect Transistor, MOSFET)。 一般是金属(metal)—氧化物(oxide)—半导体(semiconductor)场效应晶…...

System.Data.SqlClient.SqlException:“在与 SQL Server 建立连接时出现与网络相关的或特定于实例的错误
目录 背景: 过程: SQL Express的认识: 背景: 正在运行程序的时候,我遇到一个错误提示,错误信息如下,当我将错误信息仔细阅读了一番,信息提示的很明显,错误出现的来源就是连接数据库代码这块string connStr "s…...
)
数据库(SQL语句:DMLDQL)
目录 有关数据表的DML操作 1.1 INSERT 语句 1.2 REPLACE 语句 replace语句的语法格式(三种) REPLACE 语句 和 INSERT 语句的区别 1.3 DELETE 语句 | | TRUNCATE 语句 DELETE TRUNCATE DROP 1.4 UPDATE 数据 1.5 SELECT 语句 (DQL数…...

AnimatedDrawings:让绘图动起来
老样子,先上图片和官网。这个项目是让绘制的动画图片动起来,还能绑定人体的运动进行行为定制。 快速开始 1. 下载代码并进入文件夹,启动一键安装 git clone https://github.com/facebookresearch/AnimatedDrawings.gitcd AnimatedDrawingspip…...
红黑树浅浅学习
红黑树浅浅学习 红黑树概念红黑树平衡性调整 红黑树概念 二叉树:二叉树是每个节点最多有两个子树的树结构。二叉查找树:又称“二叉搜索树”,左孩子比父节点小,右孩子比父节点大,还有一个特性就是”中序遍历“可以让结…...

QGraphicsView 如何让图形大小适配窗口
1. setSceneRect 做什么用? setSceneRect是一个Qt中的函数,用于设置QGraphicsView中的场景矩形(QRectF)。 QGraphicsView是一个用于显示和编辑图形场景的控件,而setSceneRect函数用于设置场景矩形,即指定…...

sqlmap使用教程(3)-探测注入漏洞
1、探测GET参数 以下为探测DVWA靶场low级别的sql注入,以下提交方式为GET,问号(?)将分隔URL和传输的数据,而参数之间以&相连。--auth-credadmin:password --auth-typebasic (DVWA靶场需要登录…...

期待已久!阿里云容器服务 ACK AI 助手正式上线
作者:行疾 大模型技术的蓬勃发展持续引领 AI 出圈潮流,各行各业都在尝试采用 AI 工具实现智能增效。 2023 年云栖大会上,阿里云容器服务团队正式发布 ACK AI 助手,带来大模型增强智能诊断,帮助企业和开发者降低 K8s …...
[BUG] Authentication Error
前言 给服务器安装了一个todesk,但是远程一直就是,点击用户,进入输入密码界面,还没等输入就自动返回了 解决 服务器是无桌面版本,或者桌面程序死掉了,重新安装就好 sudo apt install xorg sudo apt inst…...

23种设计模式概述
学习设计模式对我们有什么帮助? 1.提高代码质量和可维护性:设计模式是经过验证的解决方案,有助于解决常见的设计问题。使用设计模式可以减少代码冗余,增强代码的可读性和可维护性,并提高代码的可靠性。 2.提升开发效率…...

英文阅读-LinkedIn‘s Tips for Highly Effective Code Review
LinkedIn的CR技巧 LinkedIn团队CodeReview经验与方法,原文来自https://thenewstack.io/linkedin-code-review/ 总结 Do I Understand the “Why”? 在提交pr的同时需要描述本次修改的“动机”,有助于提高代码文档质量。 Am I Giving Positive Feedbac…...
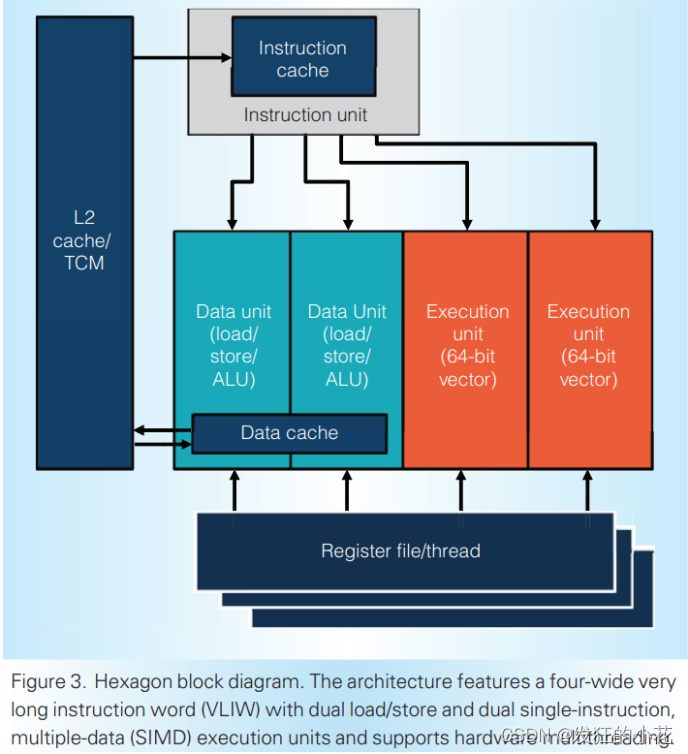
性能优化-高通的Hexagon DSP和NPU
原文来自【 Qualcomm’s Hexagon DSP, and now, NPU 】 本文主要介绍Qualcomm Hexagon DSP和NPU,这些为处理简单大量运算而设计的硬件。 🎬个人简介:一个全栈工程师的升级之路! 📋个人专栏:高性能…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...
