相关系数(皮尔逊相关系数和斯皮尔曼相关系数)
本文借鉴了数学建模清风老师的课件与思路,可以点击查看链接查看清风老师视频讲解:5.1 对数据进行描述性统计以及皮尔逊相关系数的计算方法_哔哩哔哩_bilibili
注:直接先看 ( 三、两个相关系数系数的比较 ) 部分!!!
目录
编辑
一、数据的描述性统计分析
二、皮尔逊相关系数
2.1注意事项
2.2 SPSS绘制散点图
2.3 MATLAB计算皮尔逊相关系数
2.3.1 MATLAB计算皮尔逊相关系数
2.3.2 相关系数矩阵的美化
2.4 对皮尔逊相关系数进行假设检验(p值判断法)
2.4.1 假设检验
2.4.2 MATLAB和SPSS计算p值
①MATLAB计算p值
②spss计算p值
2.5 正态分布检验
2.5.1 JB检验(大样本n > 30)
2.5.2 Shapiro-wilk检验(小样本 3 ≤ n ≤ 50)
2.5.3 QQ图
二、斯皮尔曼相关系数
2.1 斯皮尔曼相关系数
2.2 斯皮尔曼相关系数的计算
2.3 两种相关系数结果的对比
2.4 对斯皮尔曼相关系数进行假设检验(p值判断法)
①matlab计算P值
②SPSS计算p值
三、两个相关系数系数的比较
一、数据的描述性统计分析

clear;clc
%% 统计描述
MIN = min(Test); % 每一列的最小值
MAX = max(Test); % 每一列的最大值
MEAN = mean(Test); % 每一列的均值
MEDIAN = median(Test); %每一列的中位数
SKEWNESS = skewness(Test); %每一列的偏度
KURTOSIS = kurtosis(Test); %每一列的峰度
STD = std(Test); % 每一列的标准差
RESULT = [MIN;MAX;MEAN;MEDIAN;SKEWNESS;KURTOSIS;STD] %将这些统计量放到一个矩阵中表示二、皮尔逊相关系数
2.1注意事项

 简单来说,就是在进行皮尔逊相关系数之前需要绘制这两个变量的散点图查看是否为线性关系,若是就用皮尔逊,若不是就用斯皮尔曼。
简单来说,就是在进行皮尔逊相关系数之前需要绘制这两个变量的散点图查看是否为线性关系,若是就用皮尔逊,若不是就用斯皮尔曼。

上图为一般情况下相关系数的解释,实际可根据题目背景解释即可,只要言之有理即可。
2.2 SPSS绘制散点图
以这个数据为例:

这里使用Spss比较方便: 导入数据 - 图形 - 旧对话框 - 散点图/点图 - 矩阵散点图 - 将指标拖入矩阵变量(M)- 确定

这里用高版本的绘制(我用的27)感觉好看一点,如下:

注意:在得到变量之间为线性关系的时候才能继续下面的计算步骤。
2.3 MATLAB计算皮尔逊相关系数
2.3.1 MATLAB计算皮尔逊相关系数
R = corrcoef(Test) % correlation coefficient
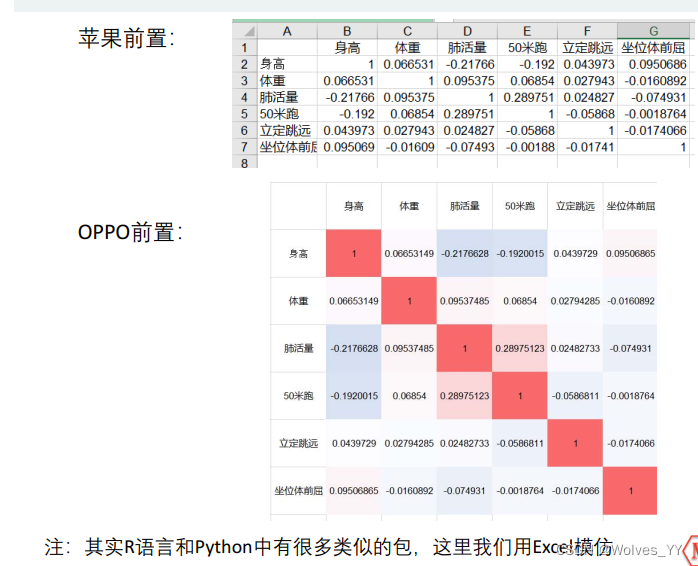
得到的R即为相关系数矩阵,其中1为自己和自己的相关性,自然为1,0.0665为第一列和第二列的相关系数,-0.2177为第一列和第三列的相关系数,0.0954为第一列和第三列的相关系数,其他的以此类推。
2.3.2 相关系数矩阵的美化
关于这里的美化,具体操作看该系列第一个视频38分钟左右处。

2.4 对皮尔逊相关系数进行假设检验(p值判断法)
2.4.1 假设检验


![]()
简单来说,就是当算出来的p值<0.01,<.05,<0.10的情况下,即在90%,95%,99%的置信水平上,拒绝原假设r = 0,因此r是显著的不为0的。(实际做的时候,就把假设和备择假设写上,然后算出p值,接着就把这段话写下来)
2.4.2 MATLAB和SPSS计算p值
①MATLAB计算p值

%% 计算各列之间的相关系数以及p值
[R,P] = corrcoef(Test)
% 在EXCEL表格中给数据右上角标上显著性符号吧
P < 0.01 % 标记3颗星的位置
(P < 0.05) .* (P > 0.01) % 标记2颗星的位置
(P < 0.1) .* (P > 0.05) % % 标记1颗星的位置但是MATLAB计算出来的p值放在Excle里,不好标记*,所以可以采用Spss。
②spss计算p值
SPSS里 分析 - 相关 - 双变量- 把变量托到右边 - 确定 。结果如下图,和matlab的结果一样:

2.5 正态分布检验
2.5.1 JB检验(大样本n > 30)


% 用循环检验所有列的数据
n_c = size(Test,2); % number of column 数据的列数
H = zeros(1,6); % 初始化节省时间和消耗
P = zeros(1,6);
for i = 1:n_c[h,p] = jbtest(Test(:,i),0.05);H(i)=h;P(i)=p;
end
disp(H)
disp(P)代码里的6是因为这里的数据变量有6个,0.05代表现在是95%的置信水平,实际中可根据需要自行调整。输出的H为1就是在95%的置信水平下拒绝原假设,即不服从正态分布,0则是不拒绝原假设,即服从正态分布;P则是p值。
2.5.2 Shapiro-wilk检验(小样本 3 ≤ n ≤ 50)

结果如下:

只需要看最后一列即可,都小于0.01,说明在99%的置信水平下,拒绝原假设,即不服从正态分布。
2.5.3 QQ图
要求样本量非常大,不太推荐用QQ图,用前面两个检验即可。

MATLAB画QQ图的命令:
% Q-Q图
qqplot(Test(:,1))二、斯皮尔曼相关系数
2.1 斯皮尔曼相关系数
第一种定义:
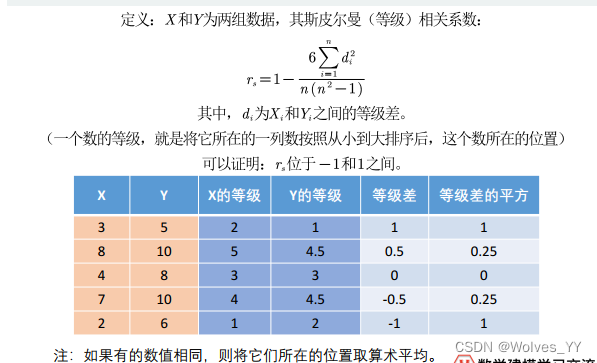

第二种定义:

2.2 斯皮尔曼相关系数的计算

第一种为只有两个变量时使用,第二种为有多个变量时使用。
2.3 两种相关系数结果的对比

2.4 对斯皮尔曼相关系数进行假设检验(p值判断法)
小样本情况下:

大样本情况下:

①matlab计算P值

②SPSS计算p值
SPSS里 分析 - 相关 - 双变量- 把变量托到右边 - 勾选上斯皮尔曼 - 确定 。
结果如下,和MATLAB结果一样的:

三、两个相关系数系数的比较

总结下来就是:
用相关系数前,先对数据进行描述性统计,然后画散点图看数据是否是线性的,接着对数据做正态性检验,满足正态性检验后再计算皮尔逊相关系数并看是不是显著的。(进行假设检验的前提是通过正态分布检验)
如果没有通过检验则用斯皮尔曼相关系数。
相关文章:

相关系数(皮尔逊相关系数和斯皮尔曼相关系数)
本文借鉴了数学建模清风老师的课件与思路,可以点击查看链接查看清风老师视频讲解:5.1 对数据进行描述性统计以及皮尔逊相关系数的计算方法_哔哩哔哩_bilibili 注:直接先看 ( 三、两个相关系数系数的比较 ) 部分&#x…...

了解 Vite 插件
众所周知 Vite 是基于 Rollup 的构建工具,Vite 插件为了优化、扩展项目构建系统功能的工具。 比如 vite-plugin-eslint 为我们提供了代码分析的功能,帮助我们在开发过程中的风格一致性。 简单示例 本文中的示例是基于 Vite Vue3.x TypeScript 来实现…...
)
算法竞赛基础:C++双向链表的结构和实现(普通链表、List、静态链表)
算法竞赛基础:双向链表 本文将会介绍在算法竞赛中双向链表的几种使用方式,适合有一定基础的人阅读。 双向链表的结构 一般来说,普通的链表结构是这样的: struct node {int num;node *next; }next指针指向下一个链表ÿ…...

openssl3.2/test/certs - 019 - ca-nonca trust variants: +serverAuth, +anyEKU
文章目录 openssl3.2/test/certs - 019 - ca-nonca trust variants: serverAuth, anyEKU概述笔记 ca-nonca.pem from exp 016openssl3.2/test/certs - 019 - ca-nonca trust variants: serverAuth, anyEKUEND openssl3.2/test/certs - 019 - ca-nonca trust variants: serverAu…...

Unity SRP 管线【第五讲:URP烘培光照】
本节,我们将跟随数据流向讲解UEP管线中的烘培光照。 文章目录 一、URP烘培光照1. 搭建场景2. 烘培光照参数设置MixedLight光照设置:直观感受 Lightmapping Settings参数设置: 3. 我们如何记录次表面光源颜色首先我们提取出相关URP代码&#…...

Mysql运维篇(一) 日志类型
一路走来,所有遇到的人,帮助过我的、伤害过我的都是朋友,没有一个是敌人,如有侵权请留言,我及时删除。 一、mysql相关日志 首先,我们能接触到的,一般我们排查慢查询时,会去看慢查询日志。如果做过数据备份会恢复的,可能接触或用过BinLog。那还有其他的吗?对MySQL原理…...

【C语言】结构体与内存操作函数 总结
结构体 一、结构体简介 C 语言内置的数据类型,除了最基本的几种原始类型,只有数组属于复合类型,可以同时包含多个值,但是只能包含相同类型的数据,实际使用中并不够用。 实际使用中,主要有下面两种情况&a…...

第12章_集合框架(Collection接口,Iterator接口,List,Set,Map,Collections工具类)
文章目录 第12章_集合框架本章专题与脉络1. 集合框架概述1.1 生活中的容器1.2 数组的特点与弊端1.3 Java集合框架体系1.4 集合的使用场景 2. Collection接口及方法2.1 添加2.2 判断2.3 删除2.4 其它 3. Iterator(迭代器)接口3.1 Iterator接口3.2 迭代器的执行原理3.3 foreach循…...

C语言进阶——数据结构之链表(续)
前言 hello,大家好呀,我是Humble,本篇博客承接之前的C语言进阶——数据结构之链表 的内容(没看过的小伙伴可以从我创建的专栏C语言进阶之数据结构 找到那篇文章并阅读后在回来哦~),上次我们重点说了链表中…...
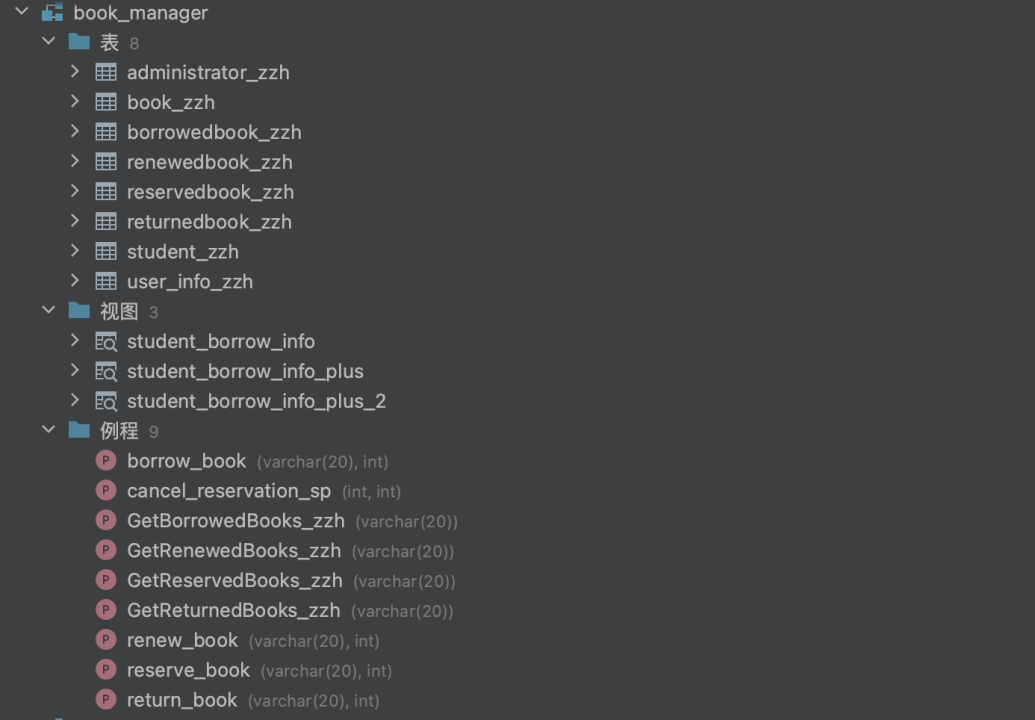
数据库课程设计-图书管理系统数据库设计
目录 一、实验目的 二、实验内容 三、实验要求 四、实验设计 4.1需求分析 4.1.1系统目标 4.1.2功能需求 4.1.3性能需求 4.14界面需求 4.2概念模型设计 4.2.1 实体及联系 4.2.2 E-R图 4.3 逻辑设计 4.3.1 E-R模型向关系模型的转换 4.3.2 数据库逻辑结构 4.3.3数据库模型函数依赖…...
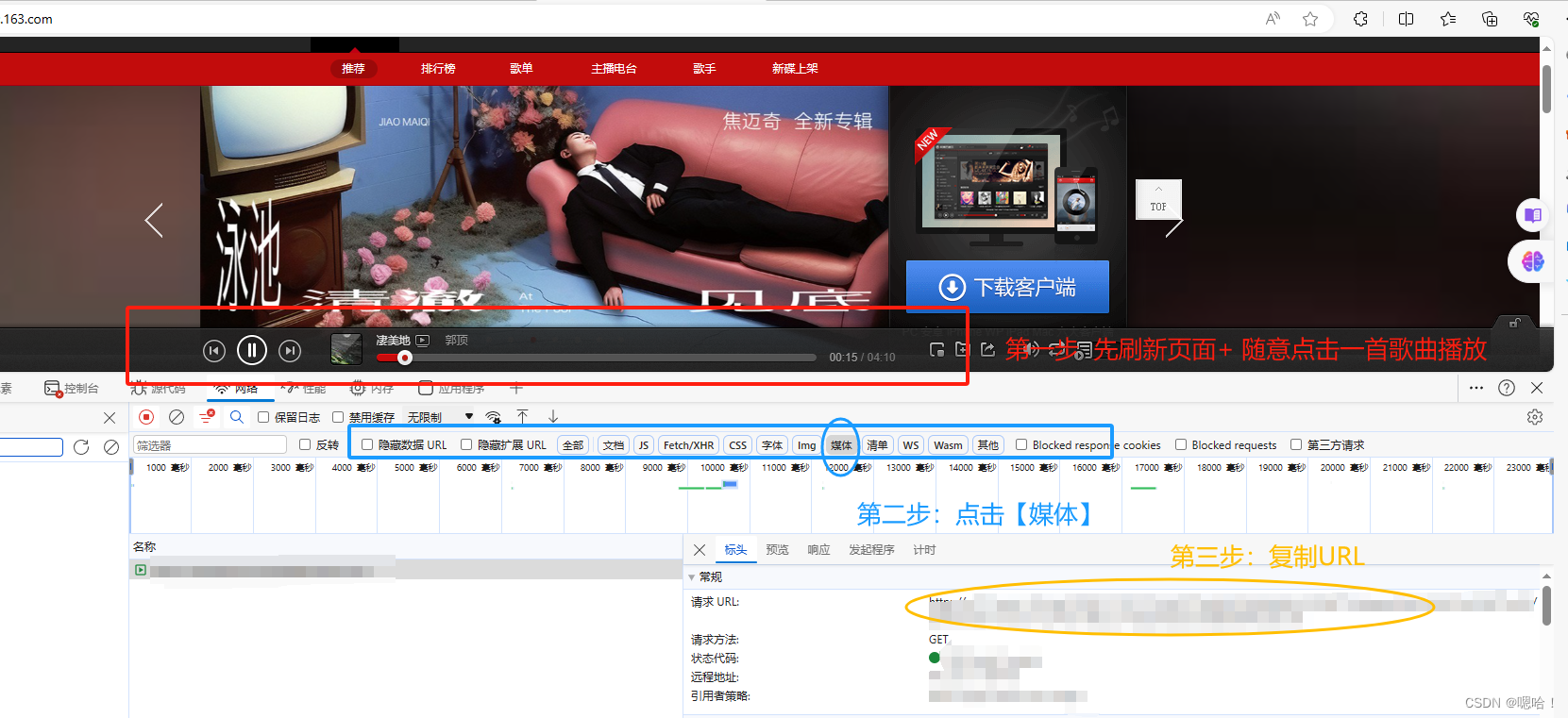
【超简版,代码可用!】【0基础Python爬虫入门——下载歌曲/视频】
安装第三方模块— requests 完成图片操作后输入:pip install requests 科普: get:公开数据 post:加密 ,个人信息 进入某音乐网页,打开开发者工具F12 选择网络,再选择—>媒体——>获取URL【先完成刷新页面】 科…...

CommunityToolkit.Mvvm支持环境
引言 CommunityToolkit.Mvvm 包(又名 MVVM 工具包,以前称为 Microsoft.Toolkit.Mvvm)是一个现代、快速和模块化的 MVVM 库。 它是 .NET 社区工具包的一部分,其中一条原则是: 独立于平台和运行时 - .NET Standard 2.0…...
探讨品牌设计的本质,为企业形象注入活力!
品牌设计作为一个行业,首先需要明确行业的本质和意义。由于越来越多的咨询公司和营销公司对品牌有不同的理解和解释,因为他们服务的内容和专业水平不同,什么是品牌的定义越来越复杂,逐渐成为一种神秘的知识。例如,特劳…...

【Maven】-- 打包添加时间戳的两种方法
一、需求 在执行 mvn clean package -Dmaven.test.skiptrue 后,生成的 jar 包带有自定义系统时间。 二、实现 方法一:使用自带属性(不推荐) 使用系统时间戳,但有一个问题,就是默认使用 UTC0 的时区。举例…...

图片分类: 多类别
最近需要训练一个有200多类的图片分类网络,搜了一遍,发现居然没有很合适用的开源项目,于是自己简单撸了一个轮子,项目地址: https://github.com/xuduo35/imgcls_pytorch。支持如下backbone: alexnetresnet18,resnet34,resnet50,r…...

python 抓包tcp数据拷贝转发
在Python中,你可以使用scapy库进行抓包,使用shutil或io库进行数据的拷贝,以及使用socket库进行数据转发。下面是一个简单的示例,展示了如何进行这些操作: 首先,你需要安装必要的库。你可以使用pip来安装它…...

ubuntu 各版本图形界面和命令行切换快捷键介绍
文章目录 前言一、ubuntu 图形界面和命令行模式切换的快捷键1. ubuntu 16.042. ubuntu 18.043. ubuntu 20.044. ubuntu 22.04 总结 前言 本文主要介绍如何使用快捷键进行ubuntu 的图形界面和命令行模式切换,涉及如下 几个ubuntu 版本 ubuntu16.04 ubuntu18.04 ubun…...
基于SpringBoot Vue博物馆管理系统
大家好✌!我是Dwzun。很高兴你能来阅读我,我会陆续更新Java后端、前端、数据库、项目案例等相关知识点总结,还为大家分享优质的实战项目,本人在Java项目开发领域有多年的经验,陆续会更新更多优质的Java实战项目&#x…...

关于预检请求
基本概述 预检请求(Preflight Request)是一种由浏览器自动发起的请求,用于检查实际请求是否安全可行。这种请求通常在跨域请求(CORS)中出现,并且只在某些特定条件下触发。以下是触发预检请求的具体条件&am…...

cookie in selenium 定时更新token
1.selenium添加cookie访问 需要登录才能访问的链接 selenium 访问 “https://developer.org.com”,如果没登陆,则跳转到"https://console.org.com/login",此时selenium取到的cookie的domain是:.console.org.com。 而domain 是 .c…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

