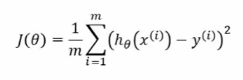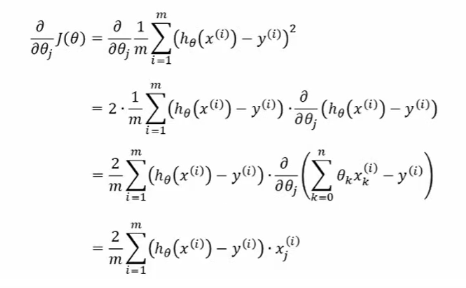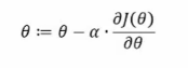机器学习实验2——线性回归求解加州房价问题
文章目录
- 🧡🧡实验内容🧡🧡
- 🧡🧡数据预处理🧡🧡
- 代码
- 缺失值处理
- 特征探索
- 相关性分析
- 文本数据标签编码
- 数值型数据标准化
- 划分数据集
- 🧡🧡线性回归🧡🧡
- 闭合形式参数求解原理
- 梯度下降参数求解原理
- 代码
- 运行结果
- 🧡🧡总结🧡🧡
🧡🧡实验内容🧡🧡
基于California Housing Prices数据集,完成关于房价预测的线性回归模型训练、测试与评估。
🧡🧡数据预处理🧡🧡
代码
"""数据预处理
"""
import pandas as pd
import numpy as np
import matplotlib.pyplot as pltdf=pd.read_csv("data/housing.csv")
df.info()### =====================填充缺失值=====================
print(df.isna().sum())
median_bedrooms = df['total_bedrooms'].median()
df['total_bedrooms'].fillna(median_bedrooms, inplace=True)### =====================特征探索=====================
df.hist(bins=50,figsize=(20,15),edgecolor="black")
plt.show()### =====================相关性分析=====================
corr_matrix=df.corr()
corr_matrix['median_house_value'].sort_values(ascending=False)### =====================组合特征=====================
df['population_per_household']=df['population']/df['households'] # 每家有几个人
df['rooms_per_household']=df['total_rooms']/df['households'] # 每家有几个房屋
df['bedrooms_per_room']=df['total_bedrooms']/df['total_rooms'] # 每个房屋有几个卧室
# corr_matrix=df.corr()
# corr_matrix['median_house_value'].sort_values(ascending=False)
df.drop(["population","households","total_rooms","total_bedrooms"],axis=1,inplace=True)### =====================文本型数据:独热编码=====================
df = pd.get_dummies(df, columns=['ocean_proximity'])### =====================连续型数据:标准化=====================
df['income_copy']=df['median_income'] # 留着后面分层抽样
con_cols=['longitude','latitude','housing_median_age','median_income','population_per_household','rooms_per_household','bedrooms_per_room','median_house_value']
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
df[con_cols] = scaler.fit_transform(df[con_cols])
df"""划分数据集
"""
### =====================划分数据集:分层抽样=====================
# 将median_income这个连续数据映射分级,放到新属性income_cat中
df['income_cat'] = pd.cut(df['income_copy'],bins=[0, 1.5, 3.0, 4.5, 6, np.inf],labels=["1", "2", "3", "4", "5"])
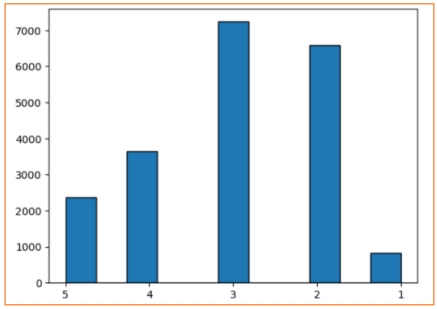
df["income_cat"].hist(edgecolor="black", bins=11, grid=False)# 分层抽样——按照income_cat属性中比例分层(它最接近符合正态分布)
from sklearn.model_selection import StratifiedShuffleSplit
ss=StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
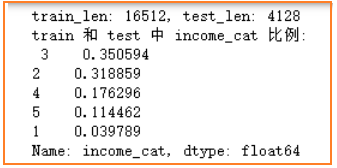
for train_idx, test_idx in ss.split(df, df['income_cat']):train_strat=df.loc[train_idx]test_strat=df.loc[test_idx]print(f"train_len: {len(train_strat)}, test_len: {len(test_strat)}")
print("train 和 test 中 income_cat 比例: \n", train_strat["income_cat"].value_counts()/len(train_strat))# 删除无用特征
df.drop(['latitude','longitude','median_house_value','income_copy','income_cat'],axis=1,inplace=True)
train_strat.drop(['income_cat','income_copy','latitude','longitude'],axis=1,inplace=True)
test_strat.drop(['income_cat','income_copy','latitude','longitude'],axis=1,inplace=True)# 划分train和test
y_train=train_strat['median_house_value'].values # .values转array
x_train=train_strat.drop('median_house_value',axis=1).values
y_test=test_strat['median_house_value'].values
x_test=test_strat.drop('median_house_value',axis=1).values
缺失值处理
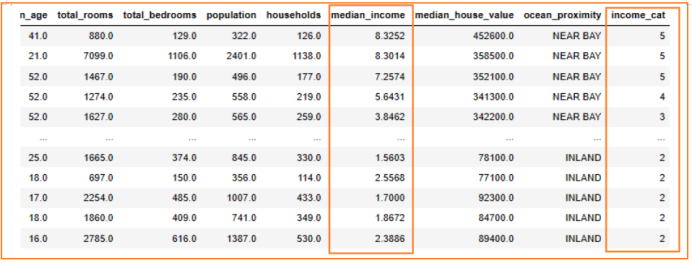
如下图,统计出total_bedrooms出现207个空值,而总样本数为20640个,大约占1%,因此可以考虑直接剔除,也可以替代,这里这个特征属于连续型变量,采用中位数替代。
特征探索
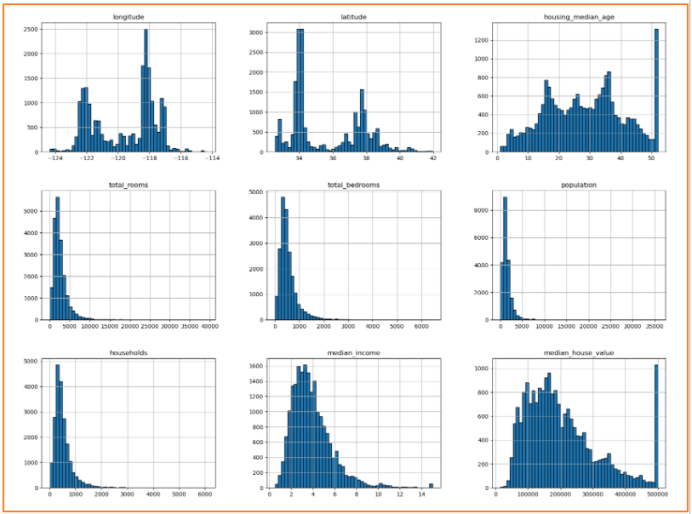
对数据集中的连续型特征绘制其直方图,总结出一些处理建议:
- 前两幅图为房地的经纬度,因此数值比较分散,不呈正态分布,情有可原
- total_rooms、total_bedrooms、population、households这几幅图很类似,同时考虑到其表达的含义比较相似,可以对它们考虑进行特征组合(后述)。另外,它们都呈现较偏左边的正态分布,右半部分比较空缺,可以考虑通过采样优化其分布(后述)。
- median_income比较接近理想的正态分布,在划分数据集时,可以考虑以它为基准进行分层抽样,这样也能保证total_rooms等特征分布呈较为合理的正态分布。
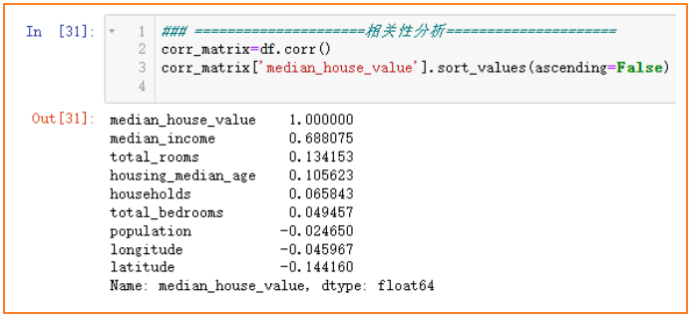
相关性分析
各个特征与房价median_house_value的相关性分析如下图,越接近1和-1越相关,0表示没有线性关系。可以看出收入median_income与房价呈很强的正相关关系,househols、total_bedrooms、popultion这几个特征对于房价来说相关性很小,结合前面特征探索中,可以将其组合出新的特征。例如
- 对于地区家庭数目households和总房屋数目total_rooms,组合成“每个家庭的房屋数量”更具有代表性。
- 对于地区卧室总数目total_bedrooms和总房屋总数目total_rooms,显然单知道两者数目比较空泛,现实生活中更看重“房间卧室的占比”,是一个衡量房价的重要指标
- 对于地区总人口和总家庭数目,可以尝试组合成“每个家庭有多少人”,可能可以从侧面反应出房间大小,进而体现房价。
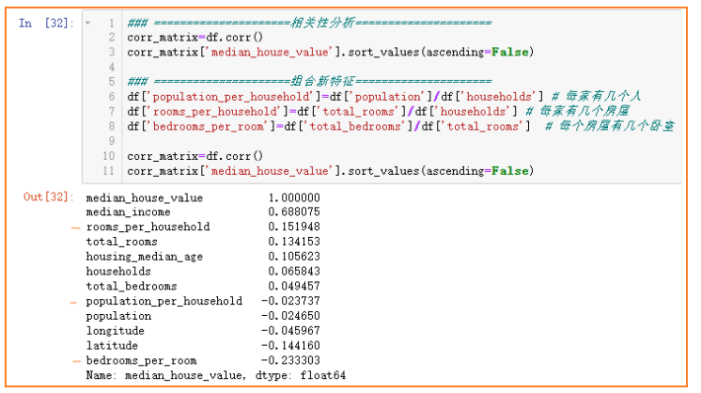
组合新特征出如下图,可以看到,新组合出的特征rooms_per_households和bedrooms_per_rom比原特征对于房价的相关性要更大,显然房间卧室的占比越小,房价越贵,符合事实。
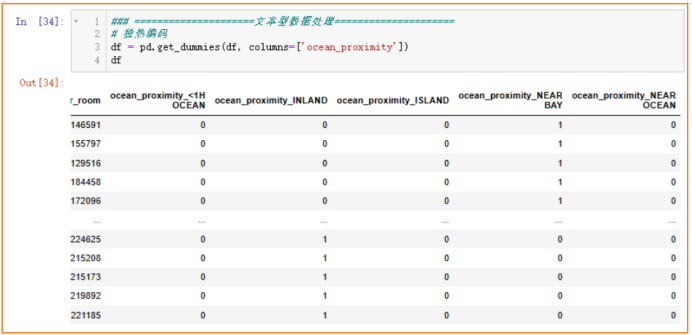
文本数据标签编码
对于地区举例海洋的距离ocean_proximity这个特征,虽然印象里认为“离海越近房价越高”(毕竟海景房更招人喜欢),考虑使用标签编码是不错的选择,但是这个特征值表示的仅是与海的距离分级,离海越接近不一定代表有更多客户青睐(毕竟能稍微远一点也能看到海景,还不用担心极端天气海边发生突发状况)。综合以上可能存在的不确定的主观因素,以及对于现实情况还不够太了解,我选择独热编码,让机器自行训练自行分辨。
数值型数据标准化
采用z-score标准化,对于每一列特征,均处理成(X-均值) / 方差。
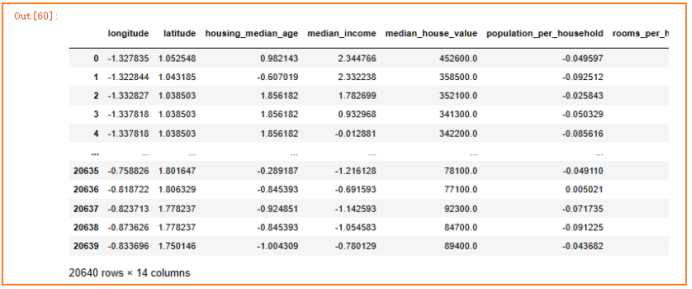
划分数据集
前面特征探索流程中,观察得出收入median_income最接近合理的正态分布,并且它与房价的相关性程度最大,因此依据不同收入median_income的等级比例来进行分层抽样。首先将连续型的收入median_income依据大小映射成不同的收入等级income_cat,并统计不同等级比例,然后依据这个等级比例分层抽样划分出训练集和测试集(即不管是在训练集和测试集中,数据比例满足收入等级对应的比例)。
🧡🧡线性回归🧡🧡
闭合形式参数求解原理
主要是通过最小化残差平方和来找到最优的回归系数
- 设要求的函数为
- 其中X为样本,θ为参数向量
- 代价函数表示为最小化残差平方和(预测值和真实值的误差):
- 对代价函数求导:
- 令导数为0:
得到如上线性回归模型的闭合形式解,能够直接计算出最优的回归系数,然而其中(XT*X)-1有时很难求解。
梯度下降参数求解原理
通过迭代优化,逐步调整回归系数以最小化损失函数,从而得到较优值对应的回归系数。
- 确定损失函数
- 计算梯度
- 梯度下降(负梯度方向)
其中α为下降的步幅(学习率),需提前设定。
重复计算梯度并且更新系数,直到达到预先设定的迭代次数或者损失函数收敛至某个阈值,本实验中通过设定每两次迭代中损失函数变化不超过1e-8,则认为损失函数收敛至某个阈值。
代码
### =====================指标评估函数=====================
def mean_absolute_error(y_true, y_pred):return np.mean(np.abs(y_pred - y_true))def mean_squared_error(y_true, y_pred):return np.mean((y_pred - y_true) ** 2)def root_mean_squared_error(y_true, y_pred):return np.sqrt(mean_squared_error(y_true, y_pred))def r_squared(y_true, y_pred):y_mean = np.mean(y_true)ss_total = np.sum((y_true - y_mean) ** 2)ss_residual = np.sum((y_true - y_pred) ** 2)r2 = 1 - (ss_residual / ss_total)return r2def goodness_of_fit(y_true, y_pred):return np.sqrt(r_squared(y_true, y_pred))### =====================求解=====================
import time## 闭合式求解法
def close_solve(X,Y):# np.linalg.inv求矩阵的逆, .T求矩阵的转置theta=np.linalg.inv(X.T.dot(X)).dot(X.T).dot(Y)return thetastart_time = time.time() # 记录程序开始时间
print("============闭合式求解:==========")
theta=close_solve(x_train, y_train)
print(f"theta: {theta}")
y_pred=np.dot(x_test,theta)
print("MAE:", mean_absolute_error(y_test, y_pred)) # 平均绝对误差
print("MSE:", mean_squared_error(y_test, y_pred)) # 均方误差
print("RMSE:", root_mean_squared_error(y_test, y_pred)) # 均方根误差
print("R方:", r_squared(y_test, y_pred)) # R方
print("拟合优度:", goodness_of_fit(y_test, y_pred)) # 拟合优度
print(f"===运行时间===:{time.time()-start_time} 秒\n")## 梯度下降法求解
# 定义损失函数
def loss_func(y_true, y_pred):return (1/2)*mean_squared_error(y_true,y_pred) # 1/2 MSEdef gradient_descent(x_train, y_train, lr):n,m=x_train.shape # 样本数目theta=np.zeros(m)while True:# 计算误差error和损失lossy_pred=np.dot(x_train, theta)error=y_pred - y_trainloss=loss_func(y_train, y_pred)# 计算梯度、更新参数gradient= 2 * np.dot(x_train.T, error) / ntheta-=lr*gradientif len(loss_histroy)!=0 and abs( loss - loss_histroy[-1]) < 1e-8: #结束条件breakloss_histroy.append(loss)return thetastart_time = time.time() # 记录程序开始时间
loss_histroy=[]
print("============梯度下降法求解:============")
theta=gradient_descent(x_train, y_train, lr=0.01)
print(f"theta: {theta}")
y_pred=np.dot(x_test,theta)
print("MAE:", mean_absolute_error(y_test, y_pred)) # 平均绝对误差
print("MSE:", mean_squared_error(y_test, y_pred)) # 均方误差
print("RMSE:", root_mean_squared_error(y_test, y_pred)) # 均方根误差
print("R方:", r_squared(y_test, y_pred)) # R方
print("拟合优度:", goodness_of_fit(y_test, y_pred)) # 拟合优度
print(f"===运行时间===:{time.time()-start_time} 秒\n")
plt.plot(loss_histroy)
plt.xlabel("iter")
plt.ylabel("loss")## print特征对应的参数
for f,t in zip(df.columns,theta):print(f"{f}\t{t}")
运行结果
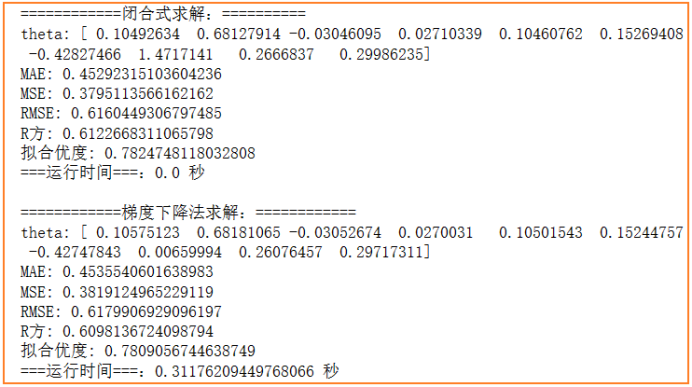
通过闭合式求解和梯度下降法求解,并用MAE、MSE、RMSE、R方、拟合优度等来比较两种求解方式的求解效果如下
可以看见,两种方法得出的结果差别不大,总体来看,闭合式求解的误差(MAE、MSE、RMSE)相对小,拟合效果(R方、拟合优度)相对大,因此在本次实验中闭合式求解的效果整体优于梯度下降法。
另外,能明显从运行时间看出两者的计算速度差异,闭合式由于只需计算结果公式(XT*X)-1X^TY,而梯度下降法中需要不断迭代更新theta很多次才能得到较优解,所以一般来说闭合式会快得多;但本实验中特征维度还算不多,闭合式会比较快,如若特征维度增多,闭合式的求解效率会变得很艰难,而梯度下降法在高纬度中仍然能以很快的速度求解出较优值。
总结来说:
- 闭合式求解法在可解的情况下,一定能求解出全局最优解,但计算速度受维度影响大,当维度较大时,可能出现不可解的情况。
- 梯度下降法不一定能求解出最优解,但在高维度时计算速度仍然有可观的效果。
🧡🧡总结🧡🧡
讨论实验结果,分析各个特征与目标预测值的正负相关性
- 呈负相关性的特征:
对于population_per_household,实验结果表明平均家庭人口越少,可能意味着住房拥挤,家庭成员较多时,每个人的居住空间和私密性可能会减少,进而可能会间接降低该地区的房价,但相关性很小,只有0.03,接近0,因此可以认为这个特征实际上对于房价影响不大,改进实验时应该不再组合这个新特征。
对于ocean_proximity_INLAND,实验结果表明靠近内陆的地区房价会越低,且相关性程度达0.42,结合实际,内陆地区由于缺乏海洋景观等吸引力因素,房价则相对较低。
- 呈正相关性的特征:
相关性程度较大的主要是收入median_income,高达0.68,结合实际考虑,高收入人群通常更愿意支付更高的房价,因此高收入区域的房价往往更高。其次主要是与海洋远近的特征,结合实际考虑,靠近海湾和靠近海洋的地区往往景色优美、气候宜人,因此房价会相应较高。
剩余特征如房龄housing_median_age、卧室占比bedrooms_per_room等等,对房价的影响程度较小。
相关文章:

机器学习实验2——线性回归求解加州房价问题
文章目录 🧡🧡实验内容🧡🧡🧡🧡数据预处理🧡🧡代码缺失值处理特征探索相关性分析文本数据标签编码数值型数据标准化划分数据集 🧡🧡线性回归🧡&am…...
宝塔+nextcloud+docker+Onlyoffice 全开启https
折腾了我三天的经验分享 1.宝塔创建网站 nextcloud版本为28.0.1 php8.2 ,导入nextcloud绑定域名对应的证书 ,不用创建mysql 因为nextcloud 要求是mariadb:10.7 宝塔里没有,就用docker安装一个 端口设置为3307 将数据库文件映射出来/ww…...

呼吸机电机控制主控MCU方案
呼吸机是一种能代替、控制或改变人的正常生理呼吸,增加肺通气量,改善呼吸功能,减轻呼吸功消耗,节约心脏储备能力的装置。呼吸机连接一条管子到患者的嘴或鼻子,氧气量可以通过监视器加以控制。 基于灵动微控制器的呼吸…...
gitlab备份-迁移-升级方案9.2.7升级到15版本最佳实践
背景 了解官方提供的版本的升级方案 - GitLab 8: 8.11.Z 8.12.0 8.17.7 - GitLab 9: 9.0.13 9.5.10 9.2.7 - GitLab 10: 10.0.7 10.8.7 - GitLab 11: 11.0.6 11.11.8 - GitLab 12: 12.0.12 12.1.17 12.10.14 - GitLab 13: 13.0.14 13.1.11 13.8.8 13.12.15 - G…...

redis面试题合集-基础
前言 又来到每日的复习时刻,昨天我们学习了mysql相关基础知识,还有分布式数据库介绍(后续总结时再持续更新)。今日继续学习缓存杀器:redis redis基础面试题合集 什么是Redis? Redis是一个开源的、内存中…...
C# 中的字符串格式化)
(Unity)C# 中的字符串格式化
前言 在软件开发中,理解和掌握字符串的格式化及调试技巧对于编写高效和可维护的代码至关重要。 字符串插值 ($ 符号) 在 C# 中,字符串插值是通过在字符串前加 $ 符号来实现的。这允许我们将变量、表达式或函数调用直接嵌入到字符串中。 string name &qu…...

【项目日记(五)】第二层: 中心缓存的具体实现(上)
💓博主CSDN主页:杭电码农-NEO💓 ⏩专栏分类:项目日记-高并发内存池⏪ 🚚代码仓库:NEO的学习日记🚚 🌹关注我🫵带你做项目 🔝🔝 开发环境: Visual Studio 2022 项目日…...
使用PSIM软件生成DSP28335流水灯程序
最近在学习DSP28335芯片,然后在使用PSIM仿真软件时发现这个仿真软件也支持28335芯片,于是就想学习下如何在PSIM软件中使用DSP28335芯片。在PSIM自带的官方示例中有使用DSP28335芯片的相关例子。 工程下载链接 https://download.csdn.net/download/qq_20…...

【iOS ARKit】人脸检测追踪基础
在计算机人工智能(Artificial Inteligence,AI)物体检测识别领域,最先研究的是人脸检测识别,目前技术发展最成熟的也是人脸检测识别。人脸检测识别已经广泛应用于安防、机场、车站、闸机、人流控制、安全支付等众多社会领域&#x…...
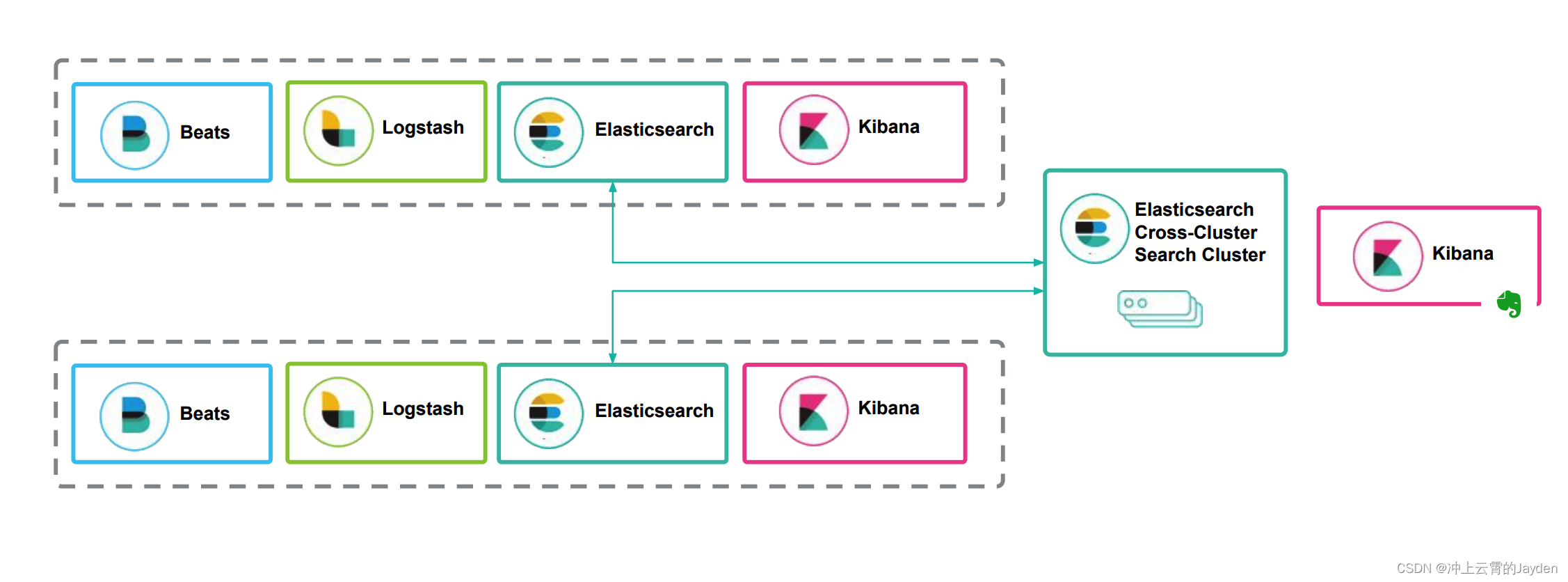
ES的一些名称和概念总结
概念 先看看ElasticSearch的整体架构: 一个 ES Index 在集群模式下,有多个 Node (节点)组成。每个节点就是 ES 的Instance (实例)。每个节点上会有多个 shard (分片), P1 P2 是主分片, R1 R2…...
Javaweb之SpringBootWeb案例之阿里云OSS服务集成的详细解析
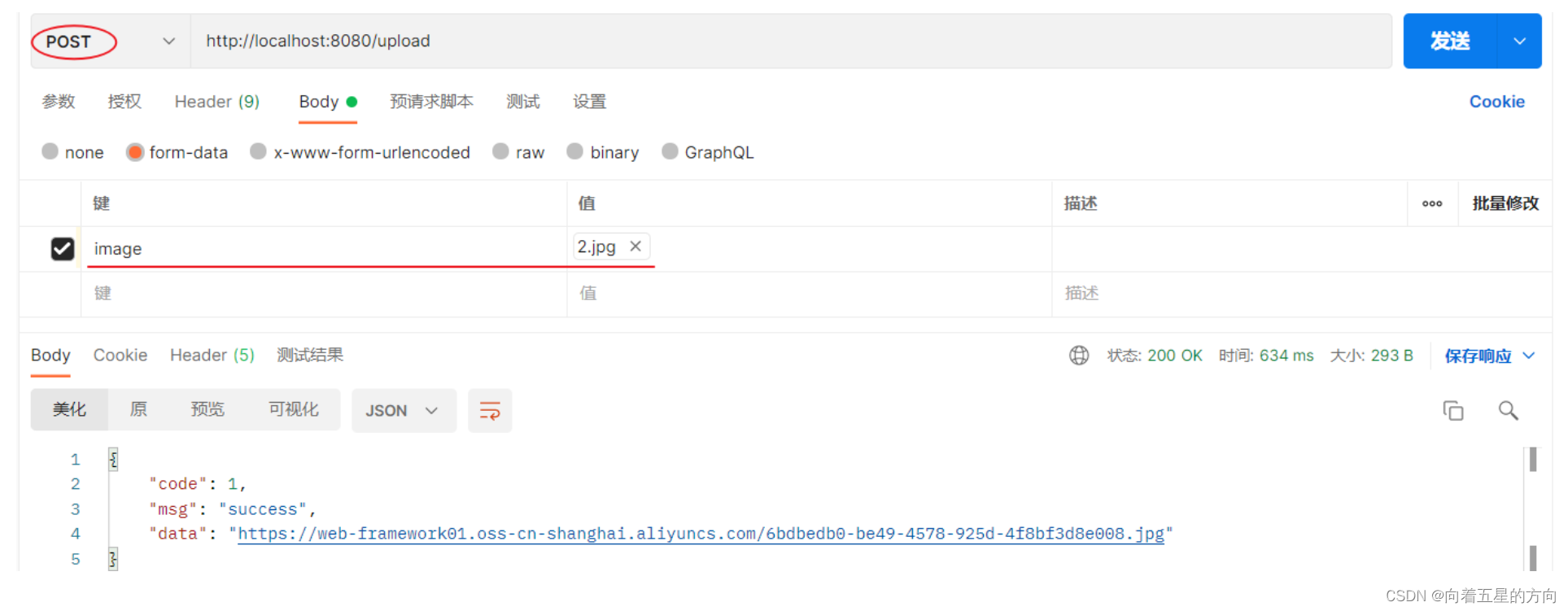
2.3.3 集成 阿里云oss对象存储服务的准备工作以及入门程序我们都已经完成了,接下来我们就需要在案例当中集成oss对象存储服务,来存储和管理案例中上传的图片。 在新增员工的时候,上传员工的图像,而之所以需要上传员工的图像&…...
【GitHub项目推荐--不错的 Go 学习项目】【转载】
开源实时性能分析平台 Pyroscope 是基于 Go 的开源实时性能分析平台,在源码中添加几行代码 pyroscope 就能帮你找出源代码中的性能问题和瓶颈、CPU 利用率过高的原因,调用树展示帮助你理解程序,支持 Go、Python、Ruby 语言。 Pyroscope 可以…...
【Git】windows系统安装git教程和配置
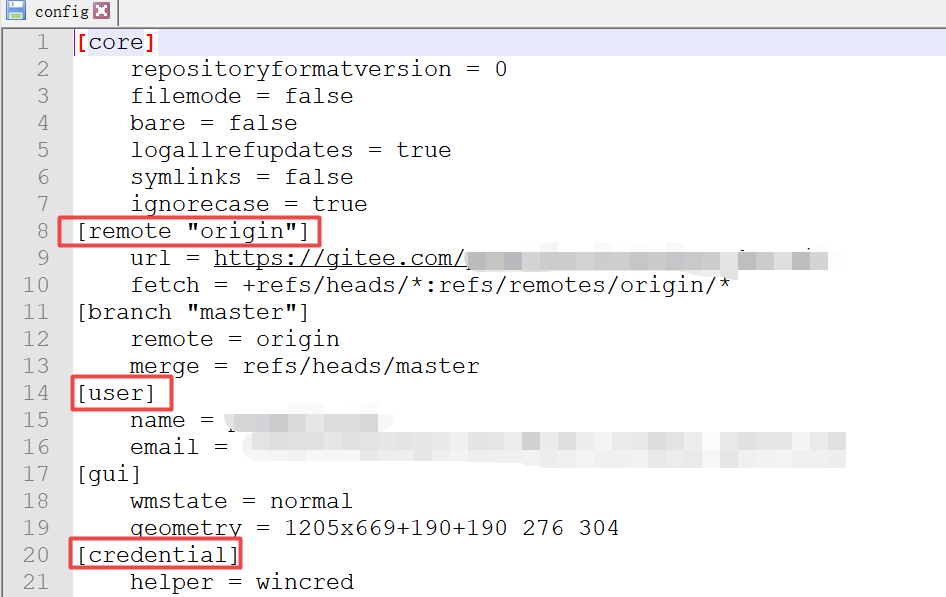
一、何为Git Git(读音为/gɪt/)是一个开源的分布式版本控制系统,可以有效、高速地处理从很小到非常大的项目版本管理。 二、git安装包 有2种版本,Git for Windows Setup和Git for Windows Portable(便携版)两个版本都可以。 三、Git for Windows Por…...

办公技巧:PPT制作技巧分享,值得收藏
目录 1、黑屏/白屏你用过么 2、图形组合替代动画刷 3、等距分布图形元素 4、快速统一字体 5、文本框也是可以改的 6、批量修改形状 7、搞定“怎么也选不中” 8、妙用CtrlD 9、图片阵列怎么做 10、临时放大某一区域 11、Word快速导入PPT 12、炫酷小人怎么做的&#…...
Google Chrome RCE漏洞 CVE-2020-6507 和 CVE-2024-0517 流程分析
本文深入研究了两个在 Google Chrome 的 V8 JavaScript 引擎中发现的漏洞,分别是 CVE-2020-6507 和 CVE-2024-0517。这两个漏洞都涉及 V8 引擎的堆损坏问题,允许远程代码执行。通过EXP HTML部分的内存操作、垃圾回收等流程方式实施利用攻击。 CVE-2020-…...

前端怎么监听手机键盘是否弹起
摘要: 开发移动端中,经常会遇到一些交互需要通过判断手机键盘是否被唤起来做的,说到判断手机键盘弹起和收起,应该都知道,安卓和ios判断手机键盘是否弹起的写法是有所不同的,下面讨论总结一下两端的区别以及…...

本地生活服务平台加盟前景与市场分析
随着短视频市场的的不断发展,人们的生活方式也在发生着巨大的变化。在这个数字化的时代,越来越多的创业者开始注重本地生活服务,这也为创业者提供了一个绝佳的商机。加盟本地生活服务平台,既可以抓住这波风口,又可以满…...

蓝桥杯备战——7.DS18B20温度传感器
1.分析原理图 通过上图我们可以看到DS18B20通过单总线接到了单片机的P14上。 2.查阅DS18B20使用手册 比赛的时候是会提供DS18B20单总线通讯协议的代码,但是没有提供读取温度数据的代码,所以还是需要我们去查看手册,我只把重要部分截下来了 …...
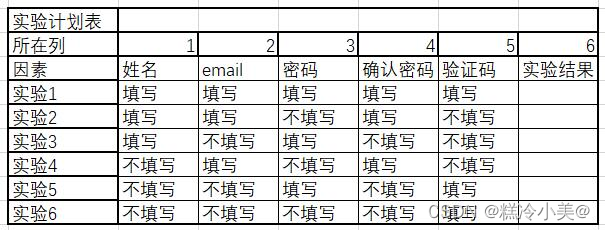
黑盒测试用例的具体设计方法(7种)
7种常见的黑盒测设用例设计方法,分别是等价类、边界值、错误猜测法、场景设计法、因果图、判定表、正交排列。 (一)等价类 1.概念 依据需求将输入(特殊情况下会考虑输出)划分为若干个等价类,从等价类中选…...
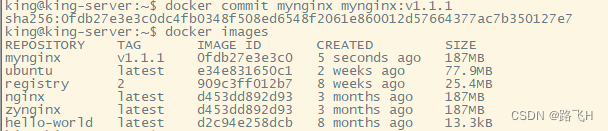
docker镜像管理命令
文章目录 docker imagesdocker builddocker rmidocker tagdocker savedocker loaddocker importdocker commitdocker login/logoutdocker pulldocker pushdocker search总结 docker images 列出本地镜像。 docker images [OPTIONS] [REPOSITORY[:TAG]]OPTIONS说明:…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...