Mamba系列日积月累(一):状态空间模型SSM的离散化过程推导
文章目录
- 1. 背景基础知识
- 1.1 什么是状态空间模型(State Space Model,SSM)?
- 1.2 什么是离散化(Discretization)?
- 1.3 为什么需要离散化?
- 2. SSM离散化过程推导
- 2.1 为什么在离散化过程中要先进行积分?
- 2.2 为什么不直接对 x ˙ ( t ) \dot{x}(t) x˙(t)进行积分?
- 2.2 状态方程的改造以及 α ( t ) \alpha(t) α(t)的设计
- 2.3 离散时间积分近似
- 2.3 状态方程的离散化
- 3. SSM离散化结果
本文首发于: Mamba系列日积月累(一):状态空间模型SSM的离散化过程推导
最近Mamba系列(Mamba、VMamba、Vision Mamba)比较火,在同样具备高效长距离建模能力的情况下,Transformer具有平方级计算复杂度,而Mamba架构则是线性级计算复杂度,并且推理速度更快。
秉承着公众号科研的思路扩展视野的思路,笔者觉得需要学习一下相关内容,于是挑选了目前较新的Vision Mamba论文,准备开始学习。由于缺乏之前的基础知识储备,Preliminaries里面的状态空间模型及其离散化过程直接给我干蒙,想着不能出师未捷身先死,于是决定搜索相关资料,把这个过程弄明白,不过由于本人水平有限,如果内容存在错误,希望大家能给出指导进行纠正。
1. 背景基础知识
1.1 什么是状态空间模型(State Space Model,SSM)?
状态空间模型(State Space Model,简称SSM)是一种数学模型,用于描述和分析动态系统的行为。这种模型在多个领域都有应用,包括控制理论、信号处理、经济学和机器学习等。在深度学习领域,状态空间模型被用来处理序列数据,如时间序列分析、自然语言处理(NLP)和视频理解等。通过将序列数据映射到状态空间,可以更好地捕捉数据中的长期依赖关系。
状态空间模型的核心思想是将系统的当前状态(state) x ( t ) ∈ R n x(t) \in \mathbb{R}^n x(t)∈Rn与输入(input) u ( t ) ∈ R p u(t) \in \mathbb{R}^p u(t)∈Rp和输出(output) y ( t ) ∈ R q y(t) \in \mathbb{R}^q y(t)∈Rq之间的关系用一组方程来表示:
x ˙ ( t ) = A ( t ) x ( t ) + B ( t ) u ( t ) y ( t ) = C ( t ) x ( t ) + D ( t ) u ( t ) (1) \begin{aligned} & \dot{x}(t)=A(t) x(t)+B(t) u(t) \\ & y(t)=C(t) x(t)+D(t) u(t) \end{aligned} \tag{1} x˙(t)=A(t)x(t)+B(t)u(t)y(t)=C(t)x(t)+D(t)u(t)(1)
- 状态方程(State Equation):描述系统状态随时间的演变。状态方程通常包含当前状态和输入,以及可能的系统参数。数学上,状态方程可以表示为: x ˙ ( t ) = A ( t ) x ( t ) + B ( t ) u ( t ) \dot{x}(t)=A(t) x(t)+B(t) u(t) x˙(t)=A(t)x(t)+B(t)u(t), 其中, x ( t ) x(t) x(t)是在时间步 t t t 的系统状态, x ˙ ( t ) \dot{x}(t) x˙(t)是状态向量 x ( t ) x(t) x(t)关于时间 t t t的导数, u ( t ) u(t) u(t) 是在时间步 t t t的输入, A ( t ) A(t) A(t)是状态转移矩阵, dim [ A ( ⋅ ) ] = n × n \operatorname{dim}[A(\cdot)]=n \times n dim[A(⋅)]=n×n, B B B 是输入矩阵, dim [ B ( ⋅ ) ] = n × p \operatorname{dim}[B(\cdot)]=n \times p dim[B(⋅)]=n×p。
- 观测方程(Observation Equation):描述系统输出与状态之间的关系。观测方程允许我们从系统的输出中观察到系统的状态。数学上,观测方程可以表示为: y ( t ) = C ( t ) x ( t ) + D ( t ) u ( t ) y(t)=C(t) x(t)+D(t) u(t) y(t)=C(t)x(t)+D(t)u(t) 其中, y ( t ) y(t) y(t) 是在时间步 t t t 的系统输出, C ( t ) C(t) C(t)是观测矩阵, dim [ C ( ⋅ ) ] = q × n \operatorname{dim}[C(\cdot)]=q \times n dim[C(⋅)]=q×n, D ( t ) D(t) D(t) 是前馈矩阵, dim [ D ( ⋅ ) ] = q × p \operatorname{dim}[D(\cdot)]=q \times p dim[D(⋅)]=q×p。
当式(1)中的所有矩阵均随着时间 t t t而变化时,此时所表示的线性时变系统,而当所有矩阵都不随时间 t t t变化时,此时表示的是线性非时变系统,在Mamba系列中,实际上是线性非时变系统:
x ˙ ( t ) = A x ( t ) + B u ( t ) y ( t ) = C x ( t ) + D u ( t ) (2) \begin{aligned} & \dot{x}(t)=A x(t)+B u(t) \\ & y(t)=C x(t)+D u(t) \end{aligned} \tag{2} x˙(t)=Ax(t)+Bu(t)y(t)=Cx(t)+Du(t)(2)
1.2 什么是离散化(Discretization)?
离散化(Discretization)是将连续的数学对象或过程转换为离散形式的过程。在不同的领域中,离散化有着不同的应用和含义,但核心思想是一致的:将连续的变量或函数映射到有限的、离散的集合中。这个过程在数学、工程、计算机科学和许多其他领域中都非常常见。
1.3 为什么需要离散化?
SSM作为一个连续时间系统,其难以直接集成到现代深度学习算法中:
- 计算效率:现代深度学习框架和硬件通常是基于离散时间操作而设计的,对SSM进行离散化后,才能将其转化为可以在这些框架和硬件上高效运行的模型。
- 训练算法:大多数深度学习训练算法,如梯度下降和反向传播,都是为离散时间模型设计的。离散化使得这些算法可以直接应用于状态空间模型,简化了训练过程。
- 实际应用:在许多实际应用中,数据是离散的,如文本数据(单词序列)、时间序列数据(股票价格、传感器读数)等。离散时间模型更自然地与这些数据格式相匹配。
- 模型复杂度:离散化过程可以通过选择合适的时间步长 T T T 来控制模型的复杂度。较小的时间步长可以提供更精细的控制,但计算成本更高;较大的时间步长可以减少计算量,但可能牺牲一些精度。
2. SSM离散化过程推导
这里再贴上状态方程公式
x ˙ ( t ) = A x ( t ) + B u ( t ) (3) \dot{x}(t)=A x(t)+B u(t) \tag{3} x˙(t)=Ax(t)+Bu(t)(3)
为了进行离散化,我们首先要对状态方程(3)进行积分。
2.1 为什么在离散化过程中要先进行积分?
在离散化连续状态方程的过程中,积分是一个关键步骤,因为它涉及到状态变量随时间的累积效应,我们需要考虑在每个离散时间步长内状态变量是如何累积变化的。
在离散时间系统中,我们不能直接处理导数,因为离散时间点上没有导数的概念。相反,我们需要考虑在每个时间步长内状态变量的累积变化。这可以通过对连续时间积分进行离散化来实现,即将连续时间的积分转换为离散时间的求和。
在实际的数值模拟中,我们通常使用数值积分方法(如梯形法则、矩形法则、辛普森法则等)来近似连续时间积分。这些方法允许我们在离散时间点上近似连续时间的累积效应,从而得到离散时间状态方程。这个转换过程涉及到将连续时间的导数项替换为离散时间的差分项,这通常涉及到指数函数和采样间隔 T T T 的计算。
2.2 为什么不直接对 x ˙ ( t ) \dot{x}(t) x˙(t)进行积分?
在式(3)中,假设我们直接对 x ˙ ( t ) \dot{x}(t) x˙(t)进行积分的话,结果如下:
x ( t ) = x ( 0 ) + ∫ 0 t ( A x ( τ ) + B u ( τ ) ) d τ (4) x(t)=x(0)+\int_0^t(A x(\tau)+B u(\tau)) d \tau \tag{4} x(t)=x(0)+∫0t(Ax(τ)+Bu(τ))dτ(4)
此时,积分项中会包含 x ( τ ) x(\tau) x(τ)项本身,由于我们是离散系统,我们是无法获取在一个连续的时刻( 0 → t 0\rightarrow t 0→t)内所有的 x ( τ ) x(\tau) x(τ)值的,因此无法完成该积分结果的计算。
对于离散系统来说,我们希望将公式(4)这个积分表达式转变为以下形式:
x ( k + 1 ) = x ( k ) + ∑ i = 0 k ( A x ( i ) + B u ( i ) ) Δ t (5) x(k+1)=x(k)+\sum_{i=0}^k(A x(i)+B u(i)) \Delta t \tag{5} x(k+1)=x(k)+i=0∑k(Ax(i)+Bu(i))Δt(5)
这个形式要求我们对公式(3)进行一些改造,目标是消除 x ˙ ( t ) \dot{x}(t) x˙(t)表达式中的 x ( t ) x(t) x(t)本身。
2.2 状态方程的改造以及 α ( t ) \alpha(t) α(t)的设计
为了消除 x ˙ ( t ) \dot{x}(t) x˙(t)表达式中的 x ( t ) x(t) x(t)本身,我们通常会构造一个新的函数 α ( t ) x ( t ) \alpha(t)x(t) α(t)x(t),通过对这个新函数进行求导,来简化相应的导数项。
我们对 α ( t ) x ( t ) \alpha(t)x(t) α(t)x(t)进行求导
d d t [ α ( t ) x ( t ) ] = α ( t ) x ˙ ( t ) + x ( t ) d α ( t ) d t (6) \frac{d}{d t}[\alpha(t) x(t)]=\alpha(t) \dot{x}(t)+x(t) \frac{d \alpha(t)}{d t} \tag{6} dtd[α(t)x(t)]=α(t)x˙(t)+x(t)dtdα(t)(6)
我们将公式(3)代入到公式(6)中,替换 x ˙ ( t ) \dot{x}(t) x˙(t):
d d t [ α ( t ) x ( t ) ] = α ( t ) ( A x ( t ) + B u ( t ) ) + x ( t ) d α ( t ) d t (7) \frac{d}{d t}[\alpha(t) x(t)]=\alpha(t) (A x(t)+B u(t))+x(t) \frac{d \alpha(t)}{d t} \tag{7} dtd[α(t)x(t)]=α(t)(Ax(t)+Bu(t))+x(t)dtdα(t)(7)
我们进一步对公式(7)进行改写,合并 x ( t ) x(t) x(t)的相关系数:
d d t [ α ( t ) x ( t ) ] = ( A α ( t ) + d α ( t ) d t ) x ( t ) + B α ( t ) u ( t ) (8) \frac{d}{d t}[\alpha(t) x(t)]=(A\alpha(t) + \frac{d \alpha(t)}{d t})x(t)+B \alpha(t) u(t) \tag{8} dtd[α(t)x(t)]=(Aα(t)+dtdα(t))x(t)+Bα(t)u(t)(8)
由于我们的目的是消除导数项中的 x ( t ) x(t) x(t),因此,我们令 x ( t ) x(t) x(t)的系数项为0即可:
A α ( t ) + d α ( t ) d t = 0 (9) A\alpha(t) + \frac{d \alpha(t)}{d t} = 0 \tag{9} Aα(t)+dtdα(t)=0(9)
此时,我们可以得到 α ( t ) \alpha(t) α(t)的表达式:
α ( t ) = e − A t (10) \alpha(t)=e^{-At} \tag{10} α(t)=e−At(10)
将 α ( t ) \alpha(t) α(t)的表达式代入公式(8)可以得到:
d d t [ e − A t x ( t ) ] = B e − A t u ( t ) (11) \frac{d}{d t}[e^{-At} x(t)]=B e^{-At} u(t) \tag{11} dtd[e−Atx(t)]=Be−Atu(t)(11)
这时我们已经完成了在导数项中消除 x ( t ) x(t) x(t)的目标,对 e − A t x ( t ) e^{-At}x(t) e−Atx(t)进行积分:
e − A t x ( t ) = x ( 0 ) + ∫ 0 t e − A τ B u ( τ ) d τ (12) e^{-At}x(t)=x(0)+\int_0^t e^{-A\tau} B u(\tau) d \tau \tag{12} e−Atx(t)=x(0)+∫0te−AτBu(τ)dτ(12)
对公式(12)进行整理:
x ( t ) = e A t x ( 0 ) + ∫ 0 t e A ( t − τ ) B u ( τ ) d τ (13) x(t)=e^{At}x(0)+\int_0^t e^{A(t-\tau)} B u(\tau) d \tau \tag{13} x(t)=eAtx(0)+∫0teA(t−τ)Bu(τ)dτ(13)
2.3 离散时间积分近似
2.3 状态方程的离散化
在离散系统中,我们需要将公式(13)转化为离散形式,大致步骤如下:
-
参数定义:采样时刻 t k t_k tk和 t k + 1 t_{k+1} tk+1,其中 k k k是采样索引, T T T是采样间隔,即 T = t k + 1 − t k T=t_{k+1}-t_k T=tk+1−tk
-
积分区间离散化:在连续时间积分中,我们通常有一个积分区间,例如从 t t t 到 t + △ t t+\triangle{t} t+△t。在离散时间系统中,我们需要将这个区间划分为 k k k 个等长的子区间,每个子区间的长度为 T T T。
在某个子区间内,公式(13)的形式变为:
x ( t k + 1 ) = e A ( t k + 1 − t k ) x ( t k ) + ∫ t k t k + 1 e A ( t k + 1 − τ ) B u ( τ ) d τ (14) x(t_{k+1})=e^{A(t_{k+1}-t_k)}x(t_{k})+\int_{t_{k}}^{t_{k+1}} e^{A(t_{k+1}-\tau)} B u(\tau) d \tau \tag{14} x(tk+1)=eA(tk+1−tk)x(tk)+∫tktk+1eA(tk+1−τ)Bu(τ)dτ(14) -
近似积分:对于每个子区间来说,考虑使用数值积分方法来近似积分,这里考虑对 u ( t ) u(t) u(t)应用零阶保持法,即假设 u ( t ) u(t) u(t)在采样时刻 t k t_k tk和 t k + 1 t_{k+1} tk+1之间是恒定的,此时,我们可以将 u ( t ) u(t) u(t)当做常数项从积分项中取出:
∫ t k t k + 1 e A ( t − τ ) B u ( τ ) d τ = ∫ t k t k + 1 e A ( t k + 1 − τ ) d τ B u ( t k ) (15) \int_{t_{k}}^{t_{k+1}} e^{A(t-\tau)} B u(\tau) d \tau = \int_{t_{k}}^{t_{k+1}} e^{A(t_{k+1}-\tau)} d \tau B u(t_k) \tag{15} ∫tktk+1eA(t−τ)Bu(τ)dτ=∫tktk+1eA(tk+1−τ)dτBu(tk)(15) -
离散时间状态方程构建:将公式(15)的积分结果代入到公式(14)中,同时使用 T = t k + 1 − t k T=t_{k+1}-t_k T=tk+1−tk进行化简,我们可以得到:
x ( t k + 1 ) = e A T x ( t k ) + ∫ t k t k + 1 e A ( t k + 1 − τ ) d τ B u ( t k ) (16) x(t_{k+1})=e^{AT}x(t_{k})+\int_{t_{k}}^{t_{k+1}} e^{A(t_{k+1}-\tau)} d \tau Bu\left(t_k\right) \tag{16} x(tk+1)=eATx(tk)+∫tktk+1eA(tk+1−τ)dτBu(tk)(16)
引入新变量 λ = t k + 1 − τ \lambda=t_{k+1}-\tau λ=tk+1−τ,对原积分进行简化得到:
x ( t k + 1 ) = e A T x ( t k ) + B u ( t k ) ∫ 0 T e A τ d τ (17) x(t_{k+1})=e^{AT}x(t_{k})+Bu\left(t_k\right)\int_{0}^{T} e^{A\tau} d \tau \tag{17} x(tk+1)=eATx(tk)+Bu(tk)∫0TeAτdτ(17)
这里涉及到矩阵作为指数的积分,这个部分我是查阅一些资料得到的结果:
∫ 0 T e A τ d τ = A − 1 ( e A T − I ) (18) \int_{0}^{T} e^{A\tau} d \tau=A^{-1}(e^{AT}- I) \tag{18} ∫0TeAτdτ=A−1(eAT−I)(18)
最终我们得到了离散时间状态方程:
x ( t k + 1 ) = e A T x ( t k ) + ( e A T − I ) A − 1 B u ( t k ) (19) x(t_{k+1})=e^{AT}x(t_{k})+(e^{AT}- I)A^{-1}B u\left(t_k\right) \tag{19} x(tk+1)=eATx(tk)+(eAT−I)A−1Bu(tk)(19)
3. SSM离散化结果
对比公式(19)和Vision Mamba论文中的离散化结果:

两者形式基本一致,至此,我们完成了SSM的离散化过程的完整推导。
相关文章:

Mamba系列日积月累(一):状态空间模型SSM的离散化过程推导
文章目录 1. 背景基础知识1.1 什么是状态空间模型(State Space Model,SSM)?1.2 什么是离散化(Discretization)?1.3 为什么需要离散化? 2. SSM离散化过程推导2.1 为什么在离散化过程中…...

React中使用LazyBuilder实现页面懒加载方法二
前言: 在一个表格中,需要展示100条数据,当每条数据里面需要承载的内容很多,需要渲染的元素也很多的时候,容易造成页面加载的速度很慢,不能给用户提供很好的体验时,懒加载是优化页面加载速度的方…...

安全测试:史上最全的攻防渗透信息收集方法、工具!
信息收集的意义 信息收集对于渗透测试前期来说是非常重要的。正所谓,知己知彼百战不殆,信息收集是渗透测试成功的保障,只有我们掌握了目标网站或目标主机足够多的信息之后,才能更好地进行渗透测试。 信息收集的方式可以分为两种…...
minio2023版本安装对象存储文件迁移
一、环境 minio版本:minio-20230320201618.0.0.x86_64.rpm 二、安装 将下载好的rpm包放在文件夹下,然后cd到该目录 sudo rpm -ivh minio-20230320201618.0.0.x86_64.rpm 三、启动 1、minio的位置 which minio cd /usr/local/bin 2、启动 (可…...

###C语言程序设计-----C语言学习(7)#(调试篇)
前言:感谢您的关注哦,我会持续更新编程相关知识,愿您在这里有所收获。如果有任何问题,欢迎沟通交流!期待与您在学习编程的道路上共同进步。 一. 程序调试 1.程序调试介绍: 程序调试是软件开发过程中非常重…...
腾讯云Linux(OpenCloudOS)安装tomcat9(9.0.85)
腾讯云Linux(OpenCloudOS)安装tomcat9 下载并上传 tomcat官网 https://tomcat.apache.org/download-90.cgi 下载完成后上传至自己想要放置的目录下 解压文件 输入tar -xzvf apache-tomcat-9.0.85.tar.gz解压文件,建议将解压后的文件重新命名为tomcat,方便后期进…...

动态添加字段和注解,形成class类,集合对象动态创建Excel列
一.需求 动态生成Excel列,因为Excel列是通过类对象字段注解来添加,在不确定Excel列数的情况下,就需要动态生成列,对应类对象字段也需要动态生成; 二.ByteBuddy字节码增强动态创建类 1.依赖 <dependencies><…...
Python爬虫---Scrapy框架---CrawlSpider
CrawlSpider 1. CrawlSpider继承自scrapy.Spider 2. CrawlSpider可以定义规则,再解析html内容的时候,可以根据链接规则提取出指定的链接,然后再向这些链接发送请求,所以,如果有需要跟进链接的需求,意思就是…...

关机恶搞小程序
1. system("shutdown")的介绍 当system函数的参数是"shutdown"时,它将会执行系统的关机命令。 具体来说,system("shutdown")的功能是向操作系统发送一个关机信号,请求关闭计算机。这将触发操作系统执行一系列…...

《HTML 简易速速上手小册》第9章:HTML5 新特性(2024 最新版)
文章目录 9.1 HTML5 新增标签和属性9.1.1 基础知识9.1.2 案例 1:创建一个结构化的博客页面9.1.3 案例 2:使用新的表单元素创建事件注册表单9.1.4 案例 3:创建一个具有高级搜索功能的搜索表单 9.2 HTML5 表单增强9.2.1 基础知识9.2.2 案例 1&a…...

计算机网络之NAT
NAT(网络地址转换,Network Address Translation)是一种网络技术,用于在一个网络与另一个网络之间重新映射IP地址。NAT最常见的应用是在家庭和小型办公室的路由器中,用于将私有(内部)IP地址转换为…...

SQL - 数据操作语句
SQL - 数据操作语句 文章目录 SQL - 数据操作语句数据操作语言-DML1 新增2 修改3 删除4 清空 数据类型1 数值类型2 字符串类型3 日期时间类型 数据操作语言-DML 概念: DML(Data Manipulation Language), 数据操作语言。对数据表数据的增、删…...
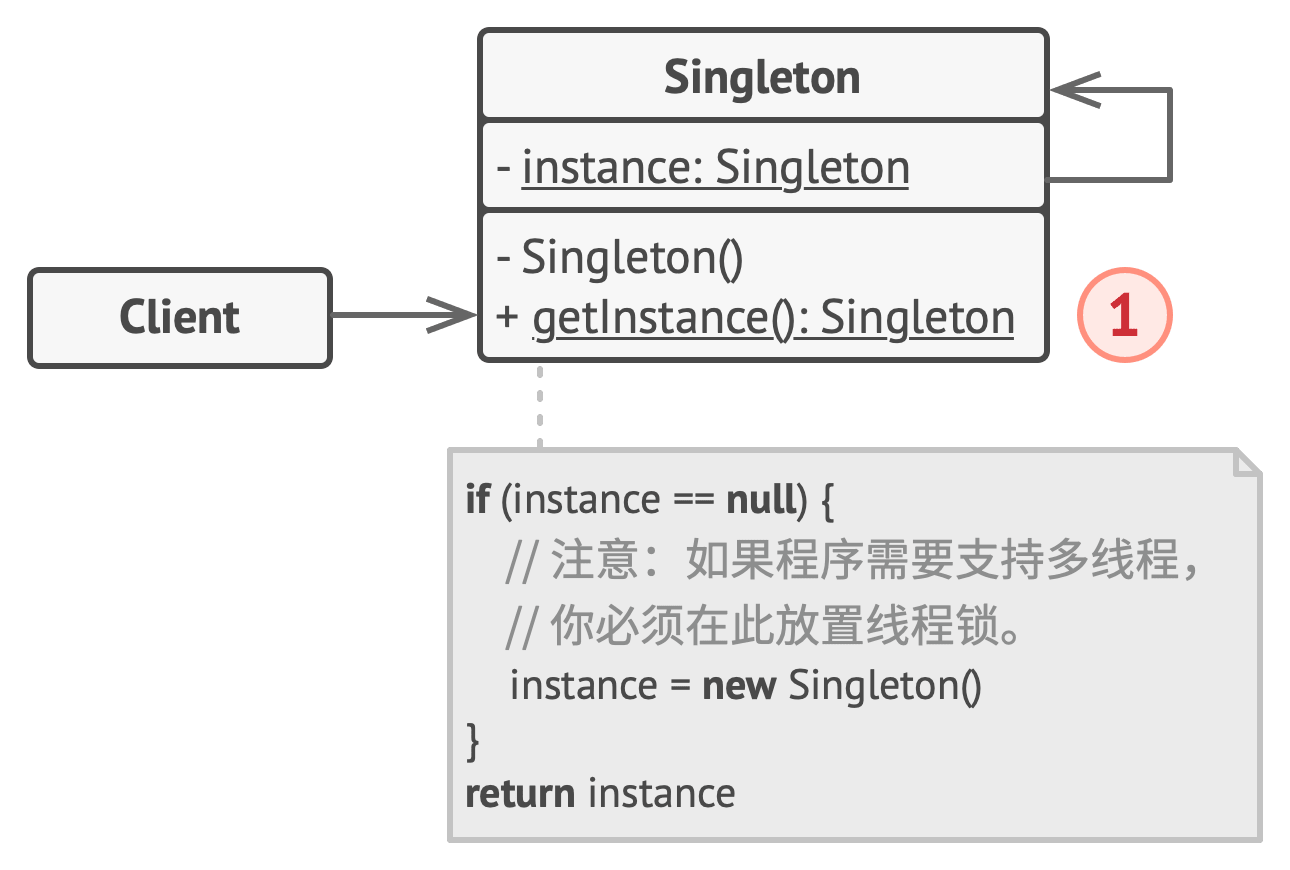
【Python笔记-设计模式】单例模式
一、说明 单例是一种创建型设计模式,能够保证一个类只有一个实例, 并提供一个访问该实例的全局节点。 (一) 解决问题 维护共享资源(数据库或文件)的访问权限,避免多个实例覆盖同一变量,引发程序崩溃。 …...

Java使用io流生成pdf文件
首先生成pdf和正常请求接口一样,直接写~ Controller层: 第一个注解:最顶层增加 Controller 注解(控制器)不多讲了 直接加上。 第二个注解:最顶层增加 CrossOrigin 注解此注解是为了浏览器请求的时候防…...
STL-priority_queue
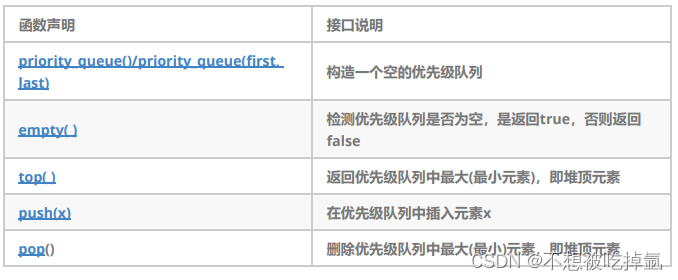
文档 目录 1.关于priority_queued1的定义 2.priority_queue的使用 1.关于priority_queued1的定义 1. 优先队列是一种容器适配器,根据严格的弱排序标准,它的第一个元素总是它所包含的元素中最大的。 2. 此上下文类似于堆,在堆中可以随时插入元…...

SpringBoot基于注解形式配置多数据源@DS
TOC() 1.引入依赖 <!-- dynamic-datasource 多数据源--><dependency><groupId>com.baomidou</groupId><artifactId>dynamic-datasource-spring-boot-starter</artifactId><version>3.5.2</version></dependency>2.配置…...

华清远见作业第三十四天——C++(第三天)
思维导图: 题目: 设计一个Per类,类中包含私有成员:姓名、年龄、指针成员身高、体重,再设计一个Stu类,类中包含私有成员:成绩、Per类对象p1,设计这两个类的构造函数、析构函数和拷贝构造函数。 代码&#…...

Shell中正则表达式
1.正则表达式介绍 1、正则表达式---通常用于判断语句中,用来检查某一字符串是否满足某一格式 2、正则表达式是由普通字符与元字符组成 3、普通字符包括大小写字母、数字、标点符号及一些其他符号 4、元字符是指在正则表达式中具有特殊意义的专用字符,…...

Flutter Canvas 属性详解与实际运用
在Flutter中,Canvas是一个强大的绘图工具,允许我们以各种方式绘制图形、文字和图像。了解Canvas的属性是开发高度定制化UI的关键。在本篇博客中,我们将深入探讨Flutter中Canvas的一些重要属性,并展示它们在实际应用中的使用。 1.…...

Django配置websocket时的错误解决
基于移动群智感知的网络图谱构建系统需要手机app不断上传数据到服务器并把数据推到前端标记在百度地图上,由于众多手机向同一服务器发送数据,如果使用长轮询,则实时性差、延迟高且服务器的负载过大,而使用websocket则有更好的性能…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

jdbc查询mysql数据库时,出现id顺序错误的情况
我在repository中的查询语句如下所示,即传入一个List<intager>的数据,返回这些id的问题列表。但是由于数据库查询时ID列表的顺序与预期不一致,会导致返回的id是从小到大排列的,但我不希望这样。 Query("SELECT NEW com…...

2025年低延迟业务DDoS防护全攻略:高可用架构与实战方案
一、延迟敏感行业面临的DDoS攻击新挑战 2025年,金融交易、实时竞技游戏、工业物联网等低延迟业务成为DDoS攻击的首要目标。攻击呈现三大特征: AI驱动的自适应攻击:攻击流量模拟真实用户行为,差异率低至0.5%,传统规则引…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...
