假设检验的过程
假设检验的核心思想是小概率事件在一次实验中不可能发生,假设检验就是利用小概率事件的发生进行反正。学习假设检验,有几个概念不能跳过,原假设、p值
1.原假设
假设检验的基本过程如下:
1)做出一个假设H0,以及它的备择假设H1,注意,H0一般实验组和对照组无差异
2)在H0成立的情况下,根据置信度构造一个小概率事件。(显著性水平一般设为5%,即在H0成立的情况下,发生的可能性,这也就是我们说的小概率事件)
显著性水平和P值是假设检验中关键的两个概念,显著性水平
是认为定义的用于判断是否是小概率事件的阈值,低于该阈值,则认为是小概率事件,也是可以接受判断发生错误的概率。
显著性水平,是当原假设H0为真时,可以容忍的第一类错误(本来正确的判断为不正确的错误,之所以
选择第一类错误进行计算标准,是因为我们觉得第一类错误更严重,比方说上了个实验,本来没效果,判断为有效果,相对于有效果,判断为没效果,对业务影响更大)发生的概率,是认为定义的小概率事件发生的最大概率值。

2.统计功效
第二类错误也应该避免,因为如果第二类错误发生的概率过高,会导致错失发展机会,因此,为了控制第二类错误,引入功效概念,即当H0不成立时,做出拒绝H0的结论正确的概率=1-第二类错误发生的概率,功效越高,发生第二类错误的概率越小。
综上,P值是小概率事件实际发生的概率,P值<,证明小概率事件发生,拒绝H0,接受H1,认为策略有效;否则,不能拒绝H0,但不代表接受H1, 我们需要进一步看功效,若功效>80%(一般情况下),证明犯第二类错误的概率很低,说明策略大概率是无效的,若功效<80%,说明有效判断为无效的概率比较大,但是也可能是真没效果,可以通过增加样本量n的方法继续观察。
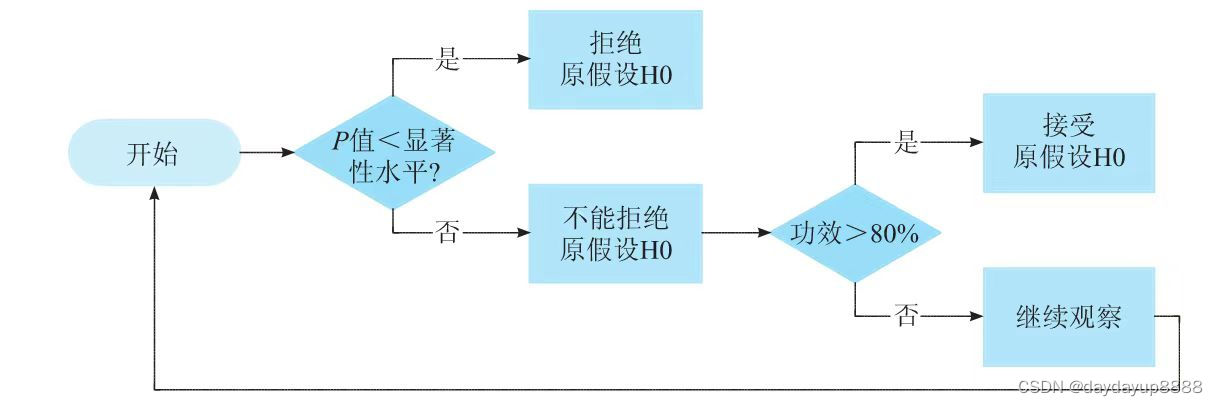
3.p值和统计功效的计算
在正态分布时,P值与t值(在下面公式中,假设了两个组别的方差是一样的)有对应关系,求p值可以转化为求检验统计量t值。在现成的t检验,输出的结果包括P值,置信区间,两个样本的均值。
通过构造t分布(是一个概率密度曲线,与正态分布很像,5%的显著性水平,对于t值>=1.96或t值<=-1.96, 双边的),计算在实际发生的概率,得到p值。
set.seed(123)
group1 <- rnorm(100, mean = 50, sd = 10)
group2 <- rnorm(100, mean = 50, sd = 10)# 使用t.test()函数进行两样本t检验
t.test(group1, group2, alternative = "two.sided")得到结果
Welch Two Sample t-testdata: group1 and group2
t = 1.4886, df = 197.35, p-value = 0.1382
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:-0.6428618 4.6019159
sample estimates:
mean of x mean of y 50.90406 48.92453 统计功效:,这里的u指的是我们认为两组数据真实的差值为u
设
公式变为
当u=0.05时,计算
相关文章:
假设检验的过程
假设检验的核心思想是小概率事件在一次实验中不可能发生,假设检验就是利用小概率事件的发生进行反正。学习假设检验,有几个概念不能跳过,原假设、p值 1.原假设 假设检验的基本过程如下: 1)做出一个假设H0,…...
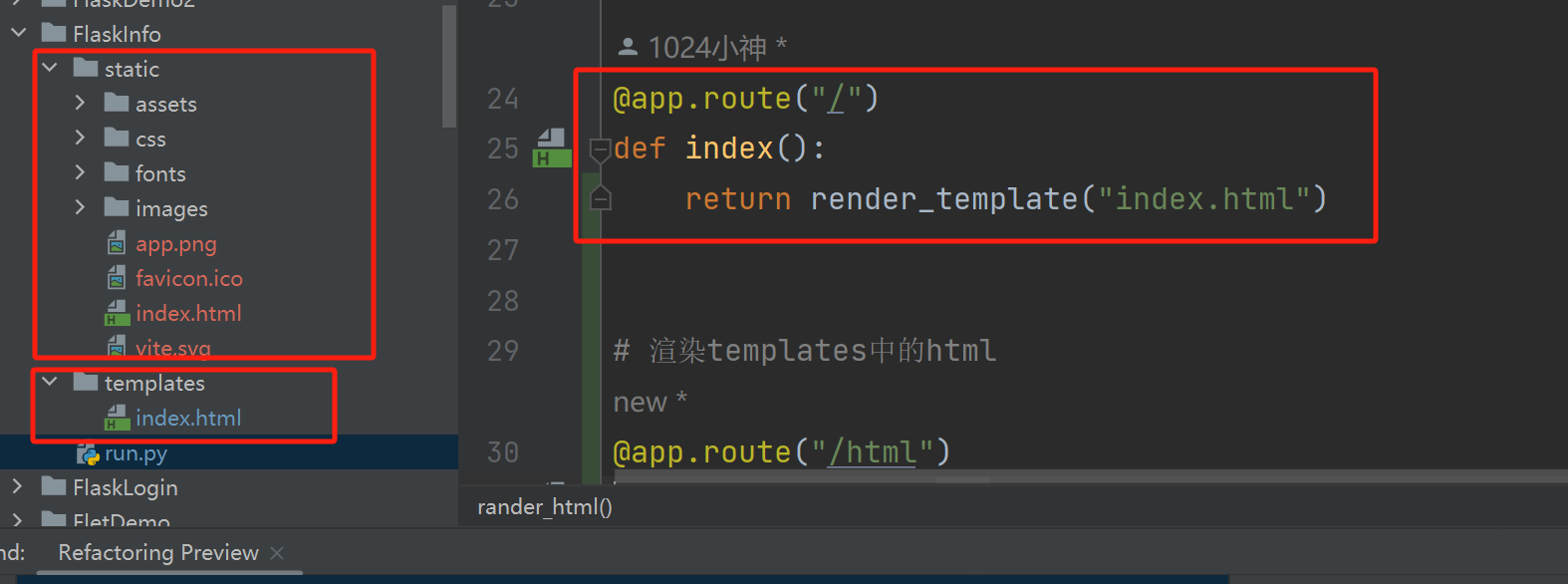
vue项目打包部署到flask等后端服务里面,实现前后端不分离部署,解决空白页面和刷新页面not fount问题
1. 编译模式一定要设置为esnext,否则会报错: Strict MIME type checking is enforced for module scripts per HTML spec.Expected a JavaScript module script but the server responded with a MIME type of "text/plain". 具体解释可以看vi…...
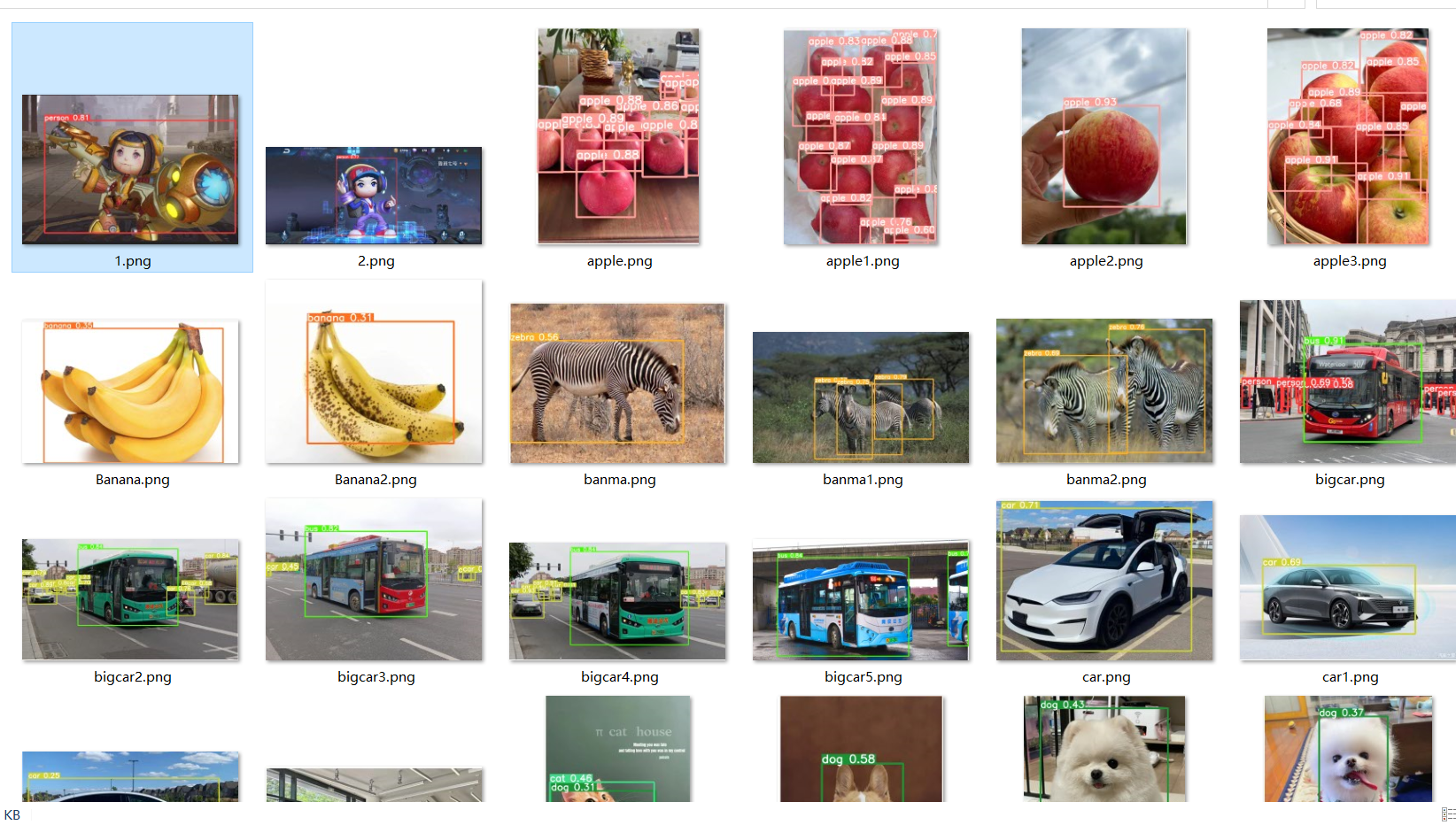
labelimg 在pycharm下载使用
labelimg 使用数据标注工具 labelimg 制作数据集 在pycharm中搜索labelimg 选择版本安装 labelimg install 使用数据标注工具制作数据集 启动 带参数启动 1、cmd cd到指定目录 2、带参数启动标注工具 左侧可以选择切换为需要的数据格式 一些快捷键 和自动保存,…...
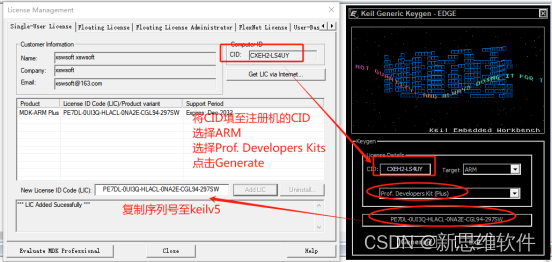
STM32/C51开发环境搭建(KeilV5安装)
Keil C51是美国Keil Software公司出品的51系列兼容单片机C语言软件开发系统,与汇编相比,C语言在功能上、结构性、可读性、可维护性上有明显的优势,因而易学易用。Keil提供了包括C编译器、宏汇编、链接器、库管理和一个功能强大的仿真调试器等…...
HTML基础)
前端开发 :(二)HTML基础
1. 介绍HTML 1.1 HTML的定义和作用 HTML(HyperText Markup Language)是一种标记语言,用于创建和设计网页的结构和内容。它通过使用标签来描述文档的结构,使得浏览器能够正确地解释和显示页面。 1.2 HTML的发展历史 HTML的发展…...

小米平板6获取root权限教程
1. 绑定账号 1> 打开"设置-我的设备-全部参数-连续点击MIUI版本按钮",直到提示已打开开发者模式( p s : 这里需要重点关注红框平板型号和 M I U I 版本,例如我这里平板型号是 X i a o m i P a d 6 , M I U I 版本是 14.0.10 &am…...
)
01. k210-命令行环境搭建(ubuntu环境)
本文主要讲解k210在ubuntu23.04操作系统中的环境搭建 1.获取工具链 github下载工具链 截止到目前最新版本是:Kendryte GNU Toolchain v8.2.0-20190409[Pre-release]。 编译好的镜像有ubuntu版本和windows版本,本章我们主要讲解的是ubuntu系统的开发环境。 Versio…...
Spring Boot3整合Redis
⛰️个人主页: 蒾酒 🔥系列专栏:《spring boot实战》 🌊山高路远,行路漫漫,终有归途。 目录 前置条件 1.导依赖 2.配置连接信息以及连接池参数 3.配置序列化方式 4.编写测试 前置条件 已经初始化好一个spr…...

算法之美_2024
算法与数据结构进阶 – liuyubobo 学习链接 : 算法与数据结构 玩转算法面试 – Leetcode真题分门别类讲解 学习链接:玩转算法面试 LLM行业领军大佬 带你转型大语言模型 学习链接:LLM 区块链 学习链接:区块链 运维测试 学…...
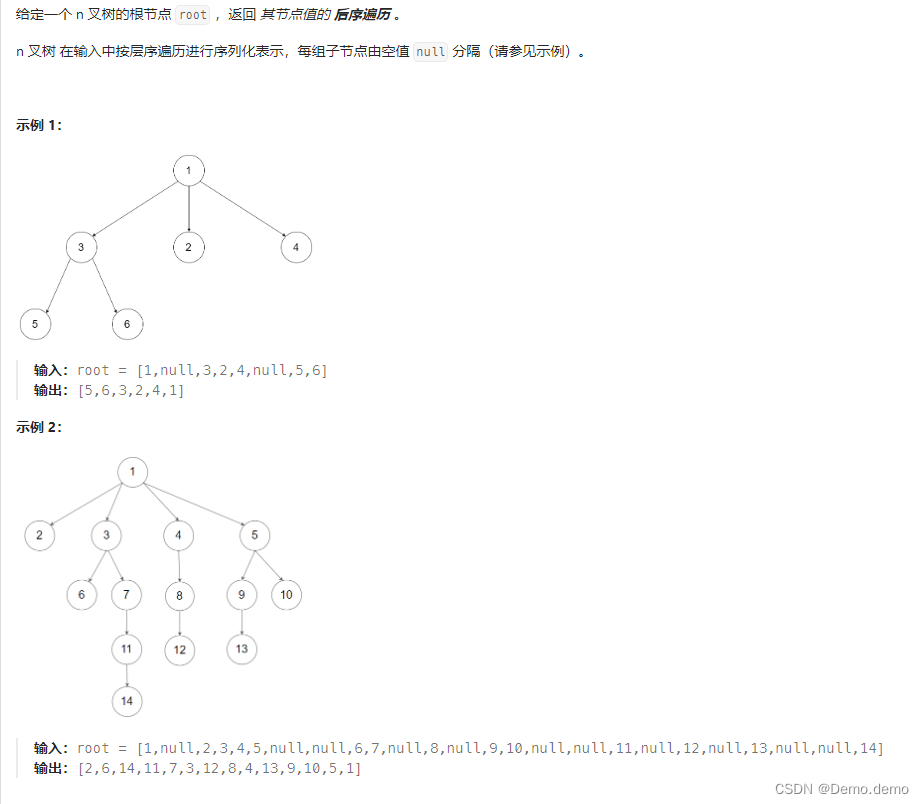
Leetcode刷题笔记题解(C++):590. N 叉树的后序遍历
思路:类似于二叉树的排序,这里需要将子树进行依次递归遍历,前序遍历也与之类似 /* // Definition for a Node. class Node { public:int val;vector<Node*> children;Node() {}Node(int _val) {val _val;}Node(int _val, vector<N…...

华为CC++语言编程规范--笔记
华为C&C语言编程规范 1.基本要求1.1 变量规则1.1.1:指针变量、表示资源描述符的变量、BOOL变量声明必须赋予初值规则1.1.2:指向资源句柄或描述符的变量,在资源释放后立即赋予新值规则1.1.3:类的成员变量必须在构造函数中赋予初…...
洛谷_P5461 赦免战俘_python写法
捋一下这道题的思路,理解了题目的意思之后我们知道这道题一定会用递归。 那递归的出口很简单,矩阵为1x1的时候就是题目所说的不能再细分下去的意思。 问题就在于递归体。 我对于递归体的理解是找到一个普适的规律,这个规律适用于每一次的递归…...
RabbitMQ的延迟队列实现[死信队列](笔记二)
上一篇已经讲述了实现死信队列的rabbitMQ服务配置,可以点击: RabbitMQ的延迟队列实现(笔记一) 目录 搭建一个新的springboot项目模仿订单延迟支付过期操作启动项目进行测试 搭建一个新的springboot项目 1.相关核心依赖如下 <dependency><groupId>org.…...

买电脑注意事项之CPU型号后面的字母都代表什么意思
在 CPU 型号后面的字母通常表示该 CPU 的一些特性或用途。不同的字母可能代表不同的系列、性能级别、功耗特性等。以下是一些常见的 CPU 后缀字母及其可能的含义: U(例如:i5-8250U): Ultra Low Power:表示低功耗&#…...
)
Transformer实战-系列教程11:SwinTransformer 源码解读4(WindowAttention类)
🚩🚩🚩Transformer实战-系列教程总目录 有任何问题欢迎在下面留言 本篇文章的代码运行界面均在Pycharm中进行 本篇文章配套的代码资源已经上传 点我下载源码 SwinTransformer 算法原理 SwinTransformer 源码解读1(项目配置/SwinTr…...
Jenkins(本地Windows上搭建)上传 Pipeline构建前端项目并将生成dist文件夹上传至指定服务器
下载安装jdk https://www.oracle.com/cn/java/technologies/downloads/#jdk21-windows 下载jenkins window版 双击安装 https://www.jenkins.io/download/thank-you-downloading-windows-installer-stable/ 网页输入 http://localhost:8088/ 输入密码、设置账号、安装推…...

Elasticsearch 安装和配置脚本文档
Elasticsearch 安装和配置脚本文档 目录 **Elasticsearch 安装和配置脚本文档**0.**概述**1.**使用方法:**2.**脚本步骤:**3. **完整代码如下:** 0.概述 此Bash脚本用于自动化在CentOS 7系统上安装和配置Elasticsearch(ES&#x…...

【Android辟邪】之:gradle——在项目间共享依赖关系版本
翻译和简单修改自:https://docs.gradle.org/current/userguide/platforms.html#sec:sharing-catalogs 建议看原文(有能力的话) 现在 Gradle 脚本可以使用两种语法编写:Kotlin 和 Groovy 本文只使用kotlin脚本语法,更…...

Qt 项目树工程,拷贝子项目dll到子项目exe运行路径
1、项目树工程 2、项目树列表 ---- BuildAll -------- App (exe) -------- Database (dll) 注:使用 子项目–>添加库–>内部库 的方式 3、qmake 内置的变量 $$OUT_PWD 表示输出文件(如可执行文件…...

进程间通信方式
1>内核提供的原始通信方式有三种 1)无名管道 2)有名管道 3)信号 2>System V提供了三种通信方式 4)消息队列 5)共享内存 6)信号量(信号灯集) 3>套接字通信 7)socke…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

字符串哈希+KMP
P10468 兔子与兔子 #include<bits/stdc.h> using namespace std; typedef unsigned long long ull; const int N 1000010; ull a[N], pw[N]; int n; ull gethash(int l, int r){return a[r] - a[l - 1] * pw[r - l 1]; } signed main(){ios::sync_with_stdio(false), …...

GraphRAG优化新思路-开源的ROGRAG框架
目前的如微软开源的GraphRAG的工作流程都较为复杂,难以孤立地评估各个组件的贡献,传统的检索方法在处理复杂推理任务时可能不够有效,特别是在需要理解实体间关系或多跳知识的情况下。先说结论,看完后感觉这个框架性能上不会比Grap…...
