P3647 题解
文章目录
- P3647 题解
- Overview
- Description
- Solution
- Lemma
- Proof
- Main
- Code
P3647 题解
Overview
很好的题,但是难度较大。
模拟小数据!——【数据删除】
Description
给定一颗树,有边权,已知这棵树是由这两个操作得到的:
Append(u, w):在 u u u 和 w w w 之间连一条红边,注意这里的 w w w 必须是新点。Insert(u, v, w):在 u u u 和 w w w, v v v 和 w w w 之间各连一条蓝边,注意这里的 w w w 必须是新点。
问蓝线的长度最大能到多少。
Solution
我们可以尝试将所有的 Insert 所产生的蓝边对都提取出来。
它们只可能有两种形式:son - u - father 和 son1 - u - son2。
Lemma
引理:所有的蓝边都可以在某一个根上表现出形如 son - u - father 的形式。
Proof
当树上没有形如 son1 - u - son2 的蓝边时,显然成立;
当树上恰好有一个形如 son1 - u - son2 的蓝边时,可以将 son1 和 son2 其中之一作为根,解决问题;
当树上有大于一个形如 son1 - u - son2 的蓝边时,可以证明不存在这样的边。
如图,当存在形如 1 的情况时,son1 和 son2 构成了单独的连通块,因为如果不是,那么 son1 和 son2 一定会是父子关系,矛盾;
当存在多个这样的连通块时,如图 2,建树时节点一定会组成单一的连通块,因为 u u u 总是存在,所以不成立。
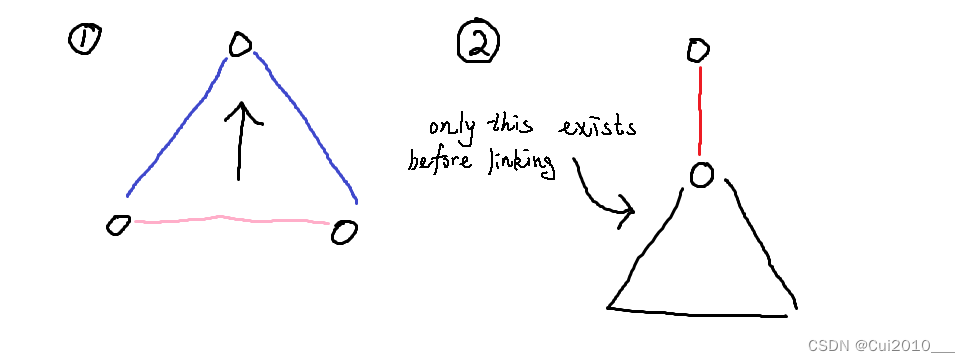
Main
有了引理,就可以树形 dp 了。
枚举树根,对每个根 DP。设 d u , 0 / 1 d_{u,0/1} du,0/1 为 u u u 为根, u u u 是否为蓝边终点的子树最大边权和。
先看 d u , 0 d_{u,0} du,0,因为没有边上的限制,所以可以任意取,对于是中点的情况,可以再加上边权 w ( u , v ) w(u,v) w(u,v),即 max ( d v , 1 + w ( u , v ) , d v , 0 ) \max(d_{v,1}+w(u,v), d_{v,0}) max(dv,1+w(u,v),dv,0)。
再看 d u , 1 d_{u,1} du,1,一定有一个 d v , 0 + w ( u , v ) d_{v,0}+w(u,v) dv,0+w(u,v),其它都是 max ( d v , 1 + w ( u , v ) , d v , 0 ) \max(d_{v,1}+w(u,v), d_{v,0}) max(dv,1+w(u,v),dv,0),所以要加上 max Δ sum \max \Delta_{\text{sum}} maxΔsum。
所以关于 d d d 的状态转移方程可以这样写:
d u , 0 = ∑ v ∈ son ( u ) max ( d v , 1 + w ( u , v ) , d v , 0 ) d u , 1 = d u , 0 + max v ∈ son ( u ) { d v , 0 + w ( u , v ) − max ( d v , 1 + w ( u , v ) , d v , 0 ) } d_{u,0} = \sum_{v\in \text{son}(u)}\max(d_{v,1}+w(u,v),d_{v,0})\\d_{u,1} = d_{u,0}+\max_{v\in \text{son}(u)}\{d_{v,0} + w(u,v) - \max(d_{v,1} + w(u,v), d_{v,0})\} du,0=v∈son(u)∑max(dv,1+w(u,v),dv,0)du,1=du,0+v∈son(u)max{dv,0+w(u,v)−max(dv,1+w(u,v),dv,0)}
这样,就可以枚举根得到 O ( n 2 ) O(n^2) O(n2) 的复杂度, 15 pts 15\text{pts} 15pts。
接下来考虑换根 DP。
一张图解释接下来两个 DP 数组的含义。
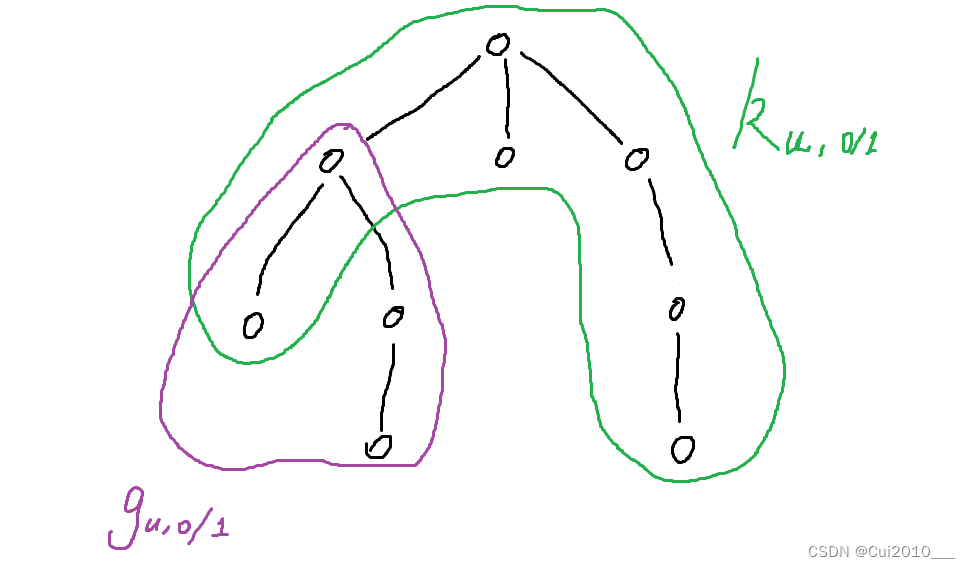
这里的 g g g 并不描述这个子树,而是以 u u u 为根的整棵树。
根据 f f f 的转移方程,我们照样也可以推出 g g g 和 k k k 的转移方程,留给读者思考。
注意到方程里仍有大量之前可以利用的内容,所以需要维护最大值和次大值。
Code
#include <bits/stdc++.h>using namespace std;int dp[200001][2], dp1[200001][2], dp2[200001][2], mx[200001], mx2[200001];vector<pair<int, int> > gv[200001];inline void add_edge(int u, int v, int w){gv[u].push_back(make_pair(v, w));gv[v].push_back(make_pair(u, w));
}void dfs(int u, int fa){vector<int> vec;vec.push_back(INT_MIN), vec.push_back(INT_MIN);for(auto v : gv[u]){if(v.first == fa) continue;dfs(v.first, u);dp[u][0] += max(dp[v.first][0], dp[v.first][1] + v.second);vec.push_back(dp[v.first][0] + v.second - max(dp[v.first][0], dp[v.first][1] + v.second));}sort(vec.begin(), vec.end(), greater<int>());mx[u] = vec[0], mx2[u] = vec[1];dp[u][1] = dp[u][0] + mx[u];
}void dfs1(int u, int fa, int lst){for(auto v : gv[u]){if(v.first == fa) continue;int tmp = dp[v.first][0] + v.second - max(dp[v.first][0], dp[v.first][1] + v.second);dp2[u][0] = dp1[u][0] - max(dp[v.first][0], dp[v.first][1] + v.second);dp2[u][1] = dp2[u][0] + (mx[u] == tmp ? mx2[u] : mx[u]);if(fa + 1) dp2[u][1] = max(dp2[u][1], dp2[u][0] + dp2[fa][0] + lst - max(dp2[fa][0], dp2[fa][1] + lst));dp1[v.first][0] = dp[v.first][0] + max(dp2[u][0], dp2[u][1] + v.second);
// dp1[v.first][1] = dp1[v.first][0] + max(mx[v.first], dp2[u][0] + v.second - max(dp2[u][0], dp2[u][1] + v.second));dfs1(v.first, u, v.second);}
}void init_vars(){// type your initiating code...
}void solve(int testcase, ...){init_vars();int n; cin >> n;for(int i = 0; i < n - 1; i++){int u, v, w; cin >> u >> v >> w;add_edge(u, v, w);}dfs(1, -1); dp1[1][0] = dp[1][0];dfs1(1, -1, 0);int ans = 0;for(int i = 1; i <= n; i++){//cout << mx[i] << " " << mx2[i] << endl;ans = max(ans, dp1[i][0]);}cout << ans << endl;
}signed main(){
#ifdef filesfreopen(".in", "r", stdin);freopen(".out", "w", stdout);
#endifios::sync_with_stdio(0);cin.tie(0), cout.tie(0);solve(1);
#ifdef filesfclose(stdin); fclose(stdout);
#endifreturn 0;
}/** things to check* 1. int overflow or long long memory need* 2. recursion/array/binary search/dp/loop bounds* 3. precision* 4. special cases(n=1,bounds)* 5. delete debug statements* 6. initialize(especially multi-tests)* 7. = or == , n or m ,++ or -- , i or j , > or >= , < or <=* 8. keep it simple and stupid* 9. do not delete, use // instead* 10. operator priority* 11. is there anything extra to output?* 12. THINK TWICE CODE ONCE, THINK ONCE DEBUG FOREVER* 13. submit ONCE, AC once. submit twice, WA forever* 14. calm down and you'll get good rank* 15. even a bit wrong scores zero* 16. ...**//** something to think about* 1. greedy? dp? searching? dp with matrix/ segment tree? binary search? ...?* 2. If it is difficult, why not the opposite?**//*########## ############ ##### ######### ##### #### ####
#### ##### #### ####
#### ########## #### ####
#### ##### #####
#### ##### ######### ##### ################ ############# #####
*/相关文章:

P3647 题解
文章目录 P3647 题解OverviewDescriptionSolutionLemmaProof Main Code P3647 题解 Overview 很好的题,但是难度较大。 模拟小数据!——【数据删除】 Description 给定一颗树,有边权,已知这棵树是由这两个操作得到的࿱…...
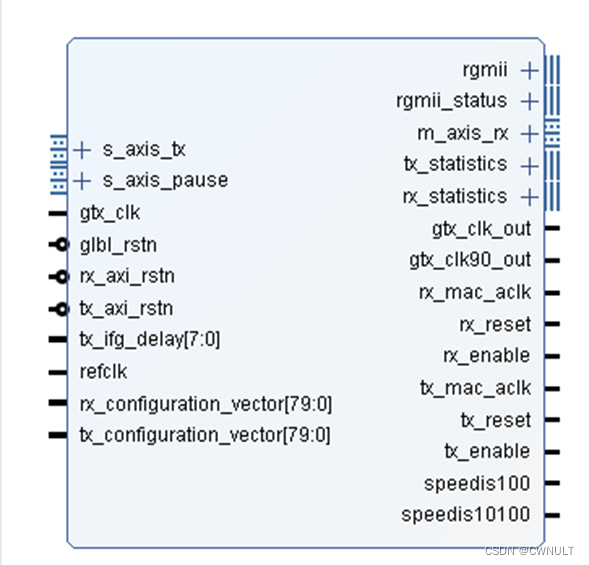
Vivado Tri-MAC IP的例化配置(三速以太网IP)
目录 1 Tri-MAC IP使用RGMII接口的例化配置1.1 Data Rate1.2 interface配置1.3 Shared Logic配置1.4 Features 2 配置完成IP例化视图 1 Tri-MAC IP使用RGMII接口的例化配置 在网络设计中,使用的IP核一般为三速以太网IP核,使用时在大多数场景下为配置为三…...
交友系统---让陌生人变成熟悉人的过程。APP小程序H5三端源码交付,支持二开。
随着社交网络的发展和普及,人们之间的社交模式正在发生着深刻的变革。传统的线下交友方式已经逐渐被线上交友取而代之。而同城交友正是这一趋势的产物,它利用移动互联网的便利性,将同城内的人们连接在一起,打破了时空的限制&#…...

uni-app 经验分享,从入门到离职(三)——关于 uni-app 生命周期快速了解上手
文章目录 📋前言⏬关于专栏 🎯什么是生命周期🧩应用生命周期📌 关于 App.vue/App.uvue 🧩页面生命周期📌关于 onShow 与 onLoad 的区别 🧩组件生命周期 📝最后 📋前言 这…...

PostgreSQL 与 MySQL 相比,优势何在?
我们将通过一张对比表格详细列出 PostgreSQL 与 MySQL 在不同方面的对比: 对比表格 特性/数据库PostgreSQLMySQL数据类型支持支持JSON/JSONB、数组、区间等高级数据类型基本数据类型支持,JSON支持较普通遵循SQL标准更严格遵循,支持复杂查询…...

Linux(三)--文件系统
Linux命令简介 [rootlocalhost ~]# 表示 Linux 系统的命令提示符。 []:这是提示符的分隔符号,没有特殊含义。 root:显示的是当前的登录用户,笔者现在使用的是 root 用户登录。 :分隔符号,没有特殊含义。 l…...
DC-8靶机渗透详细流程
信息收集: 1.存活扫描: arp-scan -I eth0 -l └─# arp-scan -I eth0 -l Interface: eth0, type: EN10MB, MAC: 00:0c:29:dd:ee:6a, IPv4: 192.168.10.129 Starting arp-scan 1.10.0 with 256 hosts (https://github.com/royhills/arp-scan) 192.168.10…...
SolidWorks学习笔记——入门知识2
目录 建出第一个模型 1、建立草图 2、选取中心线 3、草图绘制 4、拉伸 特征的显示与隐藏 改变特征名称 5、外观 6、渲染 建出第一个模型 1、建立草图 图1 建立草图 按需要选择基准面。 2、选取中心线 图2 选取中心线 3、草图绘制 以对称图形举例,先画出…...
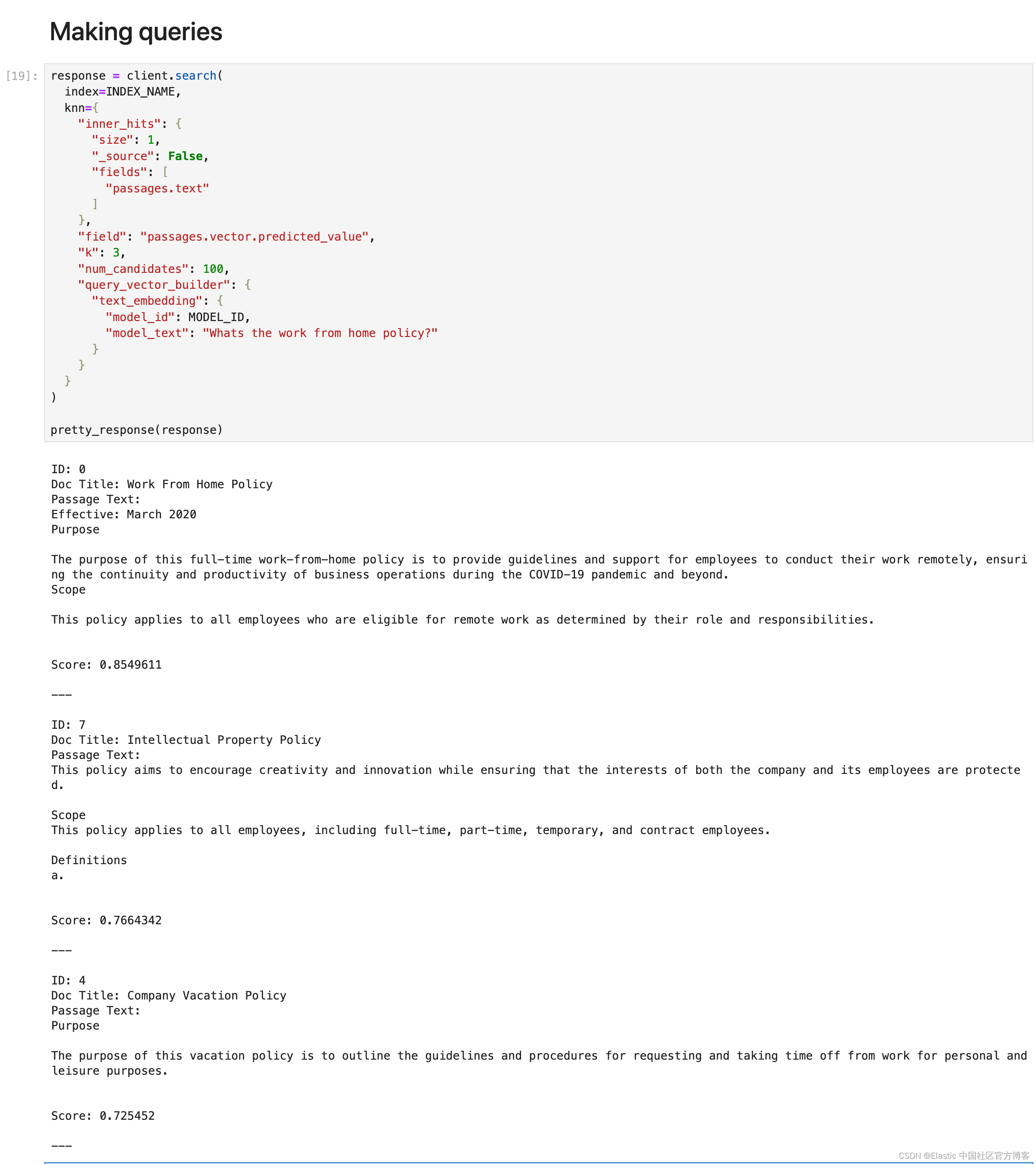
Elasticsearch:通过 ingest pipeline 对大型文档进行分块
在我之前的文章 “Elasticsearch:使用 LangChain 文档拆分器进行文档分块” 中,我详述了如何通过 LangChain 对大的文档进行分块。那个分块的动作是通过 LangChain 在 Python 中进行实现的。对于使用版权的开发者来说,我们实际上是可以通过 i…...
数据库管理-第148期 最强Oracle监控EMCC深入使用-05(20240208)
数据库管理148期 2024-02-08 数据库管理-第148期 最强Oracle监控EMCC深入使用-05(20240208)1 性能主页2 ADDM Spotlight3 实时ADDM4 数据库的其他5 主机总结 数据库管理-第148期 最强Oracle监控EMCC深入使用-05(20240208) 作者&am…...

Bug2- Hive元数据启动报错:主机被阻止因连接错误次数过多
错误代码: 在启动Hive元数据时,遇到了以下错误信息: Caused by: java.sql.SQLException: null, message from server: "Host 192.168.252.101 is blocked because of many connection errors, unblock with mysqladmin flush-hosts&qu…...
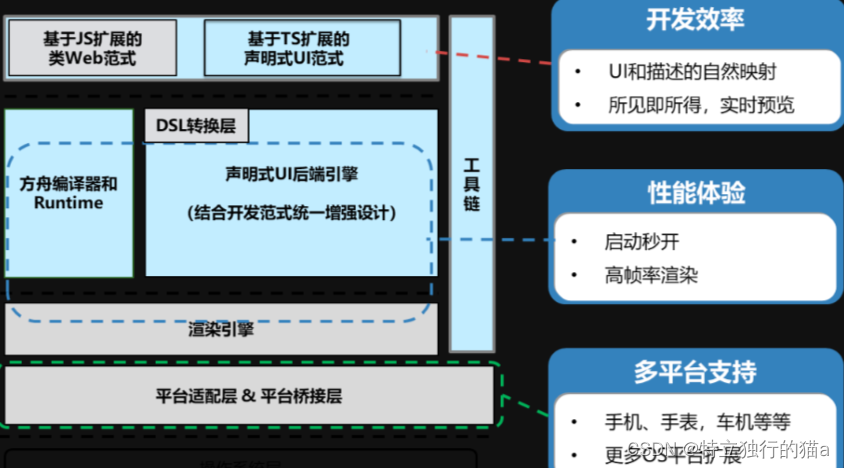
HarmonyOS 鸿蒙应用开发(十、第三方开源js库移植适配指南)
在前端和nodejs的世界里,有很多开源的js库,通过npm(NodeJS包管理和分发工具)可以安装使用众多的开源软件包。但是由于OpenHarmony开发框架中的API不完全兼容V8运行时的Build-In API,因此三方js库大都需要适配下才能用。 移植前准备 建议在适…...

Docker- chapter 1
note 1: docker 利用 volume 进行 presist data。 eg : compose.yaml: volumes:database: //# named db by self list golbal volumes: docker volume ls # the volumes on the disk inpect someone volume: docker volume inspect m…...
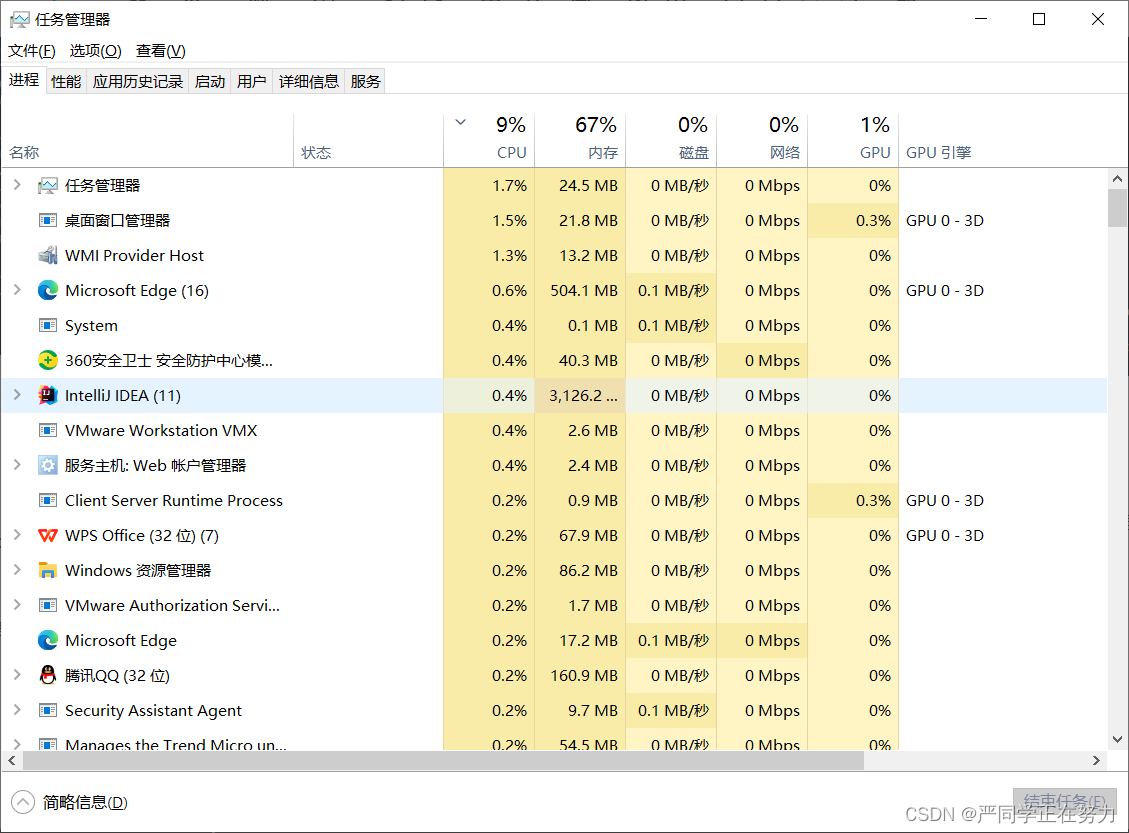
解决IntellIJ Idea内存不足
突然有一天我在IDEA打开两个项目时,发生了报错,说我内存不足,我这电脑内存16G怎么会内存不足。下面是我的解决方案。 IntelliJ IDEA 报告内存不足的原因通常与以下几个因素有关: 项目规模较大:如果您正在开发的项目非…...
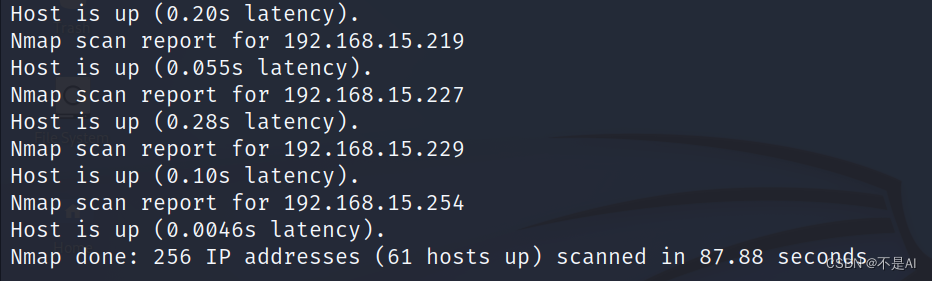
【网络技术】【Kali Linux】Nmap嗅探(二)多设备扫描
上期实验博文:(一)简单扫描 一、实验环境 本次实验进行Nmap多设备扫描,实验使用 Kali Linux 虚拟机(扫描端)、Ubuntu 22.04虚拟机(被扫描端1)、Ubuntu 18.04虚拟机(被扫…...
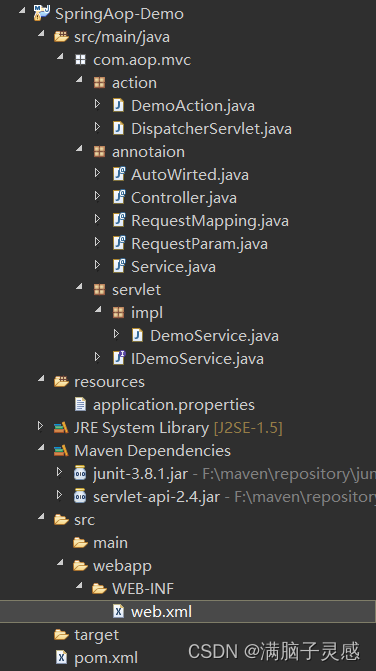
简化版SpringMVC
简化版SpringMVC web.xml xml version"1.0" encoding"UTF-8"?> <web-app version"2.5" xmlns"http://java.sun.com/xml/ns/javaee" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance" xsi:schemaLocation&quo…...
Java密码校验(正则表达式):密码由这四种元素组成(数字、大写字母、小写字母、特殊字符),且必须包含全部四种元素;密码长度大于等于8个字符。
1. 需求 对用户密码的强度进行校验,要求用户密码达到一定的强度,符合安全性要求。 1.1. 基础版需求 密码必须由字母和数字组成(同时包括数字和数字);密码长度大于等于8个字符。 1.2. 进阶版需求 密码由这四种元素…...

【AMI】2400 环境安装步骤
2400 环境安装步骤 ----------Ubuntu14.4 MDS4.0 加载代码需要勾上Update Installing SPX related packages sudo apt install gcc-multilib mtd-utils:i386 subversion patch patchutils bison sudo apt install libc6-dev libxml-dom-perl zlib1g zlib1g-dev libcurl4-ope…...

AI:124-基于深度学习的人体遮挡物体重建技术
🚀点击这里跳转到本专栏,可查阅专栏顶置最新的指南宝典~ 🎉🎊🎉 你的技术旅程将在这里启航! 从基础到实践,深入学习。无论你是初学者还是经验丰富的老手,对于本专栏案例和项目实践都有参考学习意义。 ✨✨✨ 每一个案例都附带有在本地跑过的关键代码,详细讲解供…...

23种设计模式之单例模式
目录 什么是单例模式 单例模式的优点 创建单例模式的三大要点 单例模式的实现方式 饿汉模式 懒汉模式 使用场景 什么是单例模式 单例模式是一种创建型设计模式,它的核心思想是保证一个类只有一个实例,并提供一个全局访问点来访问这个实例。 什…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...

高效的后台管理系统——可进行二次开发
随着互联网技术的迅猛发展,企业的数字化管理变得愈加重要。后台管理系统作为数据存储与业务管理的核心,成为了现代企业不可或缺的一部分。今天我们要介绍的是一款名为 若依后台管理框架 的系统,它不仅支持跨平台应用,还能提供丰富…...
