2024.1.29力扣每日一题——自由之路
2024.1.29
- 题目来源
- 我的题解
- 方法一 动态规划
题目来源
力扣每日一题;题序:514
我的题解
方法一 动态规划
定义 dp[i][j] 表示从前往后拼写出 key的第 i个字符, ring 的第 j个字符与 12:00 方向对齐的最少步数(下标均从 0 开始)。
显然,只有当字符串 ring 的第 j个字符需要和 key 的第 i 个字符相同时才能拼写出 key 的第 i 个字符,因此对于 key 的第 i个字符,需要考虑计算的 ring 的第 j 个字符只有 key[i] 在 ring 中出现的下标集合。对每个字符维护一个位置数组 pos[i],表示字符 ii在 ring 中出现的位置集合,用来加速计算转移的过程。
对于状态 dp[i][j],需要枚举上一次与 12:00 方向对齐的位置 k,因此可以列出如下的转移方程:
dp [ i ] [ j ] = min k ∈ p o s [ k e y [ i − 1 ] ] { d p [ i − 1 ] [ k ] + min { abs ( j − k ) , n − abs ( j − k ) } } \textit{dp}[i][j]=\min_{k \in pos[key[i-1]]}\{dp[i-1][k]+\min\{\text{abs}(j-k),n-\text{abs}(j-k)\}\} dp[i][j]=mink∈pos[key[i−1]]{dp[i−1][k]+min{abs(j−k),n−abs(j−k)}}
其中 min { abs ( j − k ) , n − abs ( j − k ) } \min\{\text{abs}(j-k),n-\text{abs}(j-k)\} min{abs(j−k),n−abs(j−k)} 表示在当前第 k 个字符与 12:00方向对齐时第 j 个字符旋转到 12:00 方向并按下拼写的最少步数。
最后答案即为 min i = 0 n − 1 { dp [ m − 1 ] [ i ] } + m \min_{i=0}^{n-1}\{\textit{dp}[m-1][i]\}+m mini=0n−1{dp[m−1][i]}+m。
时间复杂度: O( m n 2 mn^2 mn2)
空间复杂度: O(mn)
public int findRotateSteps(String ring, String key) {int n = ring.length(), m = key.length();//存储每个字符所在的位置List<Integer>[] pos = new List[26];for (int i = 0; i < 26; ++i) {pos[i] = new ArrayList<Integer>();}for (int i = 0; i < n; ++i) {pos[ring.charAt(i) - 'a'].add(i);}int[][] dp = new int[m][n];for (int i = 0; i < m; ++i) {Arrays.fill(dp[i], Integer.MAX_VALUE);}for (int i : pos[key.charAt(0) - 'a']) {dp[0][i] = Math.min(i, n - i);}for (int i = 1; i < m; ++i) {for (int j : pos[key.charAt(i) - 'a']) {for (int k : pos[key.charAt(i - 1) - 'a']) {dp[i][j] = Math.min(dp[i][j], dp[i - 1][k] + Math.min(Math.abs(j - k), n - Math.abs(j - k)));}}}return Arrays.stream(dp[m - 1]).min().getAsInt()+m;}
//优化空间版本
// 考虑到每次转移状态 dp[i][] 只会从 dp[i−1][] 转移过来,因此可以利用滚动数组优化第一维的空间复杂度public int findRotateSteps(String ring, String key) {int n = ring.length(), m = key.length();List<Integer>[] pos = new List[26];for (int i = 0; i < 26; ++i) {pos[i] = new ArrayList<Integer>();}for (int i = 0; i < n; ++i) {pos[ring.charAt(i) - 'a'].add(i);}//空间优化,dp[]int[] dp = new int[n];for (int i : pos[key.charAt(0) - 'a']) dp[i] = Math.min(i, n - i);for (int i = 1; i < m; ++i) {//若当前与上一次相同则不需要转动ringif(key.charAt(i)==key.charAt(i-1))continue;for (int j : pos[key.charAt(i) - 'a']) {dp[j]=Integer.MAX_VALUE;for (int k : pos[key.charAt(i - 1) - 'a']) {dp[j] = Math.min(dp[j], dp[k] + Math.min(Math.abs(j - k), n - Math.abs(j - k)));}}}return pos[key.charAt(m - 1) - 'a'].stream().mapToInt(i -> dp[i]).min().orElse(Integer.MAX_VALUE)+m;}
有任何问题,欢迎评论区交流,欢迎评论区提供其它解题思路(代码),也可以点个赞支持一下作者哈😄~
相关文章:

2024.1.29力扣每日一题——自由之路
2024.1.29 题目来源我的题解方法一 动态规划 题目来源 力扣每日一题;题序:514 我的题解 方法一 动态规划 定义 dp[i][j] 表示从前往后拼写出 key的第 i个字符, ring 的第 j个字符与 12:00 方向对齐的最少步数(下标均从 0 开始&…...

Qt应用软件【协议篇】UDP示例
UDP协议简介 UDP(用户数据报协议)是一种无连接的网络协议,提供了简单但是不可靠的消息传输服务。与TCP不同,UDP不保证数据包的顺序、重复性或者可达性,但它在速度和效率上具有优势,特别适合那些对实时性要求高的应用,如视频流、在线游戏等。 Qt中的UDP编程 在Qt中,U…...

MyBatis之动态代理实现增删改查以及MyBatis-config.xml中读取DB信息文件和SQL中JavaBean别名配置
MyBatis之环境搭建以及实现增删改查 前言实现步骤1. 编写MyBatis-config.xml配置文件2. 编写Mapper.xml文件(增删改查SQL文)3. 定义PeronMapper接口4. 编写测试类1. 执行步骤2. 代码实例3. 运行log 开发环境构造图总结 前言 上一篇文章,我们…...

百面嵌入式专栏(面试题)内存管理相关面试题1.0
沉淀、分享、成长,让自己和他人都能有所收获!😄 📢本篇我们将介绍内存管理相关面试题 。 一、内存管理相关面试题 page数据结构中的_refcount和_mapcount有什么区别?匿名页面和高速缓存页面有什么区别?page数据结构中有一个锁,我们称为页锁,请问trylock_page()和loc…...

SpringMVC 1.请求参数检查 2.全局异常处理 3.请求参数封装为Pojo
ErrorEnum.java // 枚举所有的错误 package com.example.demo.enums;import lombok.Getter;public enum ErrorEnum {SYSTEM_ERROR(-1, "系统错误"),PARAM_ERROR(-2, "参数错误"),OK(0, "成功"),;Getterprivate final int code;Getterprivate fi…...

7机器人位姿的数学描述与坐标变
由上次刚体的空间转动直接切换为机器人相关术语。 1.机器人位姿的数学描述与坐标变换 1.1位姿描述 {B}相对于{A}的姿态描述用3x3矩阵表示为: 式中为三个单位正交主矢量,分别表示刚体坐标系{B}的三个坐标轴XBYBZB在参考系{A}中的方位,∠XBXA表…...
基于ESP8266 开发板(MCU)遥控小车
遥控小车 遥控界面 【项目源码】 第一版ESP8266 https://github.com/liyinchigithub/esp8266_car_webServerhttps://github.com/liyinchigithub/esp8266_car_webServer 第二版ESP32 GitHub - liyinchigithub/esp32-wroom-car: 嵌入式单片机 ESP32 Arduino 遥控小车&a…...

【C生万物】C语言数据类型、变量和运算符
📚博客主页:爱敲代码的小杨. ✨专栏:《Java SE语法》 | 《数据结构与算法》 | 《C生万物》 ❤️感谢大家点赞👍🏻收藏⭐评论✍🏻,您的三连就是我持续更新的动力❤️ 🙏小杨水平有…...
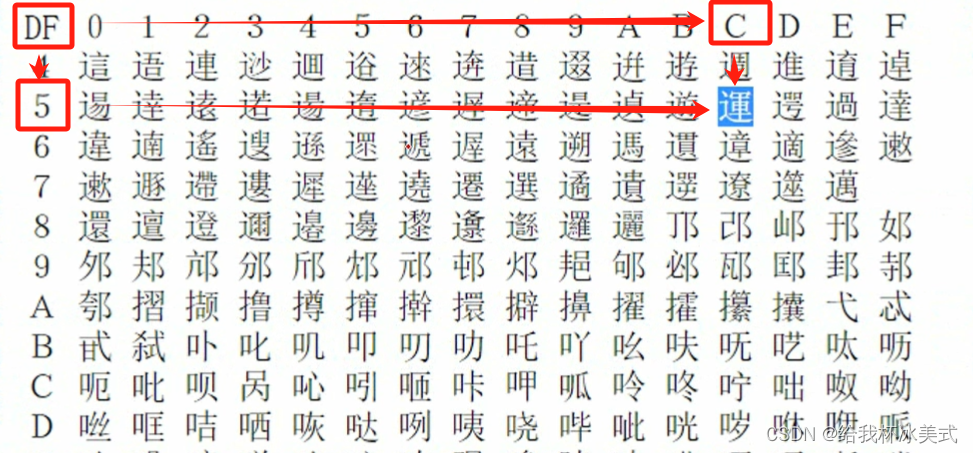
CTF--Web安全--SQL注入之‘绕过方法’
一、什么是绕过注入 众所周知,SQL注入是利用源码中的漏洞进行注入的,但是有攻击手段,就会有防御手段。很多题目和网站会在源码中设置反SQL注入的机制。SQL注入中常用的命令,符号,甚至空格,会在反SQL机制中…...

线程池常用的阻塞队列
新任务来的时候,会先判断当前运行的线程数量是否达到核心线程数,如果达到的话,新任务就会被存放在队列中。 不同的线程池会选用不同的阻塞队列,我们可以结合内置线程池来分析。 ● 容量为 Integer.MAX_VALUE 的 LinkedBlockingQue…...
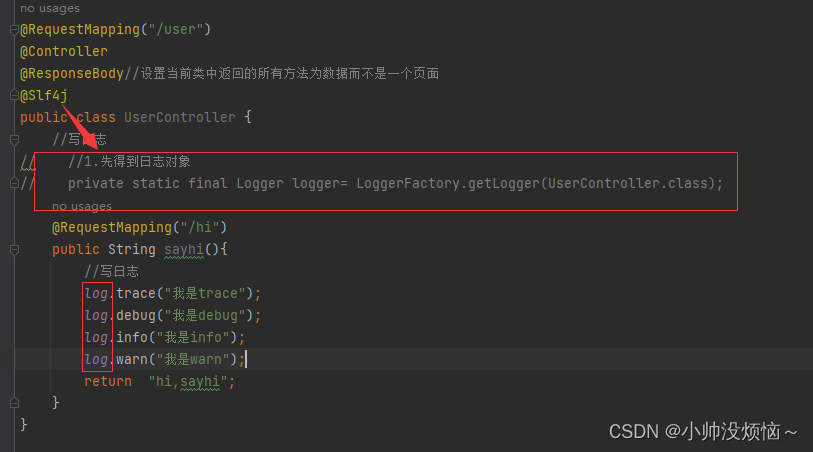
【Java EE】----SpringBoot的日志文件
1.SpringBoot使用日志 先得到日志对象通过日志对象提供的方法进行打印 2.打印日志的信息 3.日志级别 作用: 可以筛选出重要的信息不同环境实现不同日志级别的需求 ⽇志的级别分为:(1-6级别从低到高) trace:微量&#…...

【网络安全】2024年暗网威胁分析及发展预测
暗网因其非法活动而臭名昭著,现已发展成为一个用于各种非法目的的地下网络市场。 它是网络犯罪分子的中心,为被盗数据交易、黑客服务和邪恶活动合作提供了机会。为了帮助企业组织更好地了解暗网发展形势,近日,卡巴斯基的安全研究…...
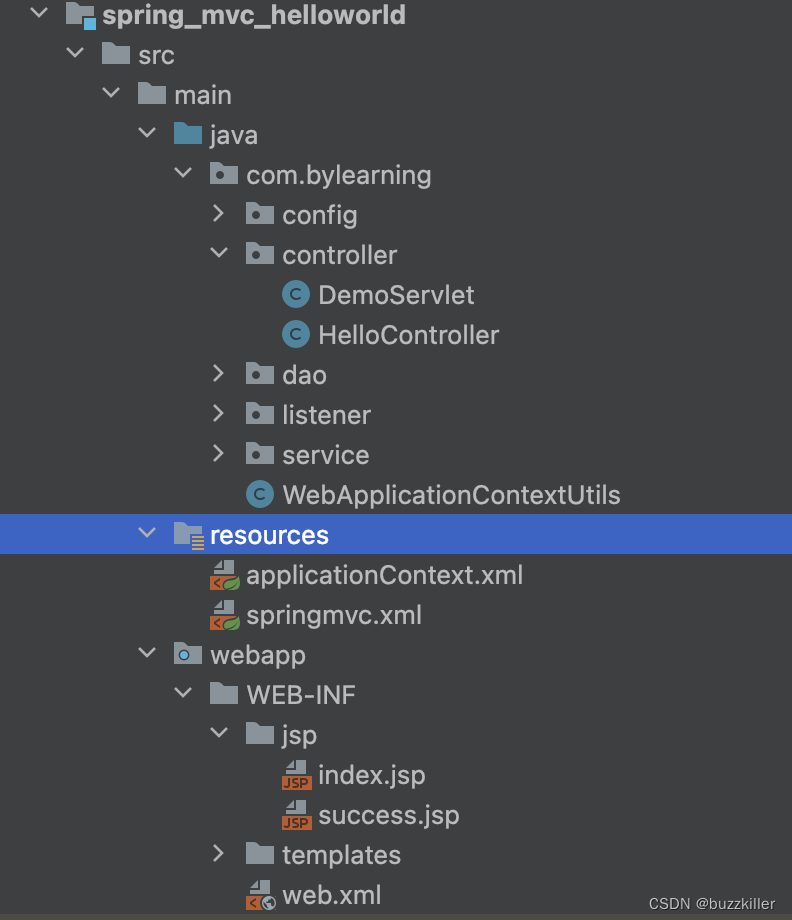
SpringMVC-组件解析
一、引子 我们在上一篇文章Spring MVC-基本概念中,为读者解释了如何使用SpringMVC框架,将承接客户端请求的工作从原生的Servlet转移到我们熟知的Controller中。那么我们不禁会好奇,SpringMVC框架到底做了什么,是怎么把请求分发给…...

ubuntu22.04@laptop OpenCV Get Started: 002_reading_writing_videos
ubuntu22.04laptop OpenCV Get Started: 002_reading_writing_videos 1. 源由2. Read/Display/Write应用Demo3 video_read_from_file3.1 C应用Demo3.2 Python应用Demo3.3 重点过程分析3.3.1 读取视频文件3.3.2 读取文件信息3.3.3 帧读取&显示 4 video_read_from_image_sequ…...
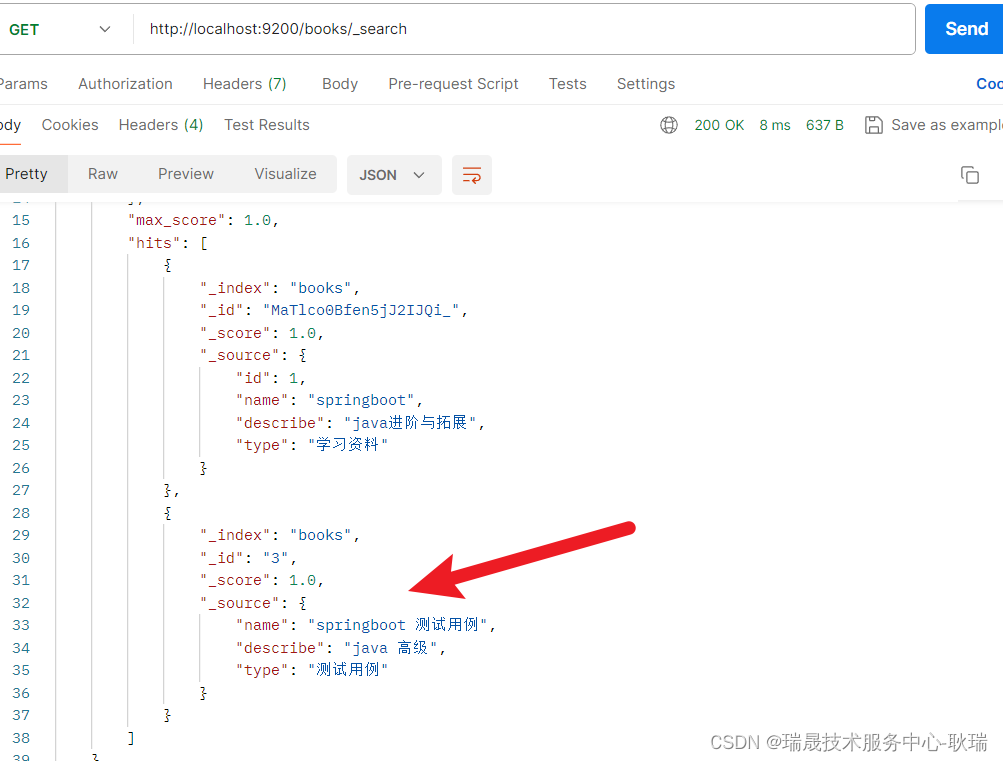
Elasticsearch(ES) 简述请求操作索引下文档 增删查改操作
上文 Elasticsearch(ES) 创建带有分词器规则的索引 带着大家创建了一个带有分词功能的索引 老规矩 我们启动一下ES服务 本文 我们就来说说 关于文档的操作 我们先来添加一个文档 就像数据库加一条数据一样 这里 并不需要指定什么表结构和数据结构 它的文档结构是无模式的 添…...

Chrome扩展开发纪要
1. 开发人员模式 以Edge(Chromium)为例, 可在管理扩展页, 在左侧开发人员模式打开, 只有此项开启后才能加载未压缩的扩展, 虽然也可以打包扩展, 但是浏览器会检测, 未上线的crx包是无法被安装的. 所以不打算上架的crx只能使用 加载解压缩的扩展 安装 2. 创建扩展 2.1 建立文…...

LeetCode-第28题-找出字符串中第一个匹配项的下标
1.题目描述 给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下标从 0 开始)。如果 needle 不是 haystack 的一部分,则返回 -1 。 2.样例描述 3.思路描述 可以让字符串 …...

分享90个行业PPT,总有一款适合您
分享90个行业PPT,总有一款适合您 90个行业PPT下载链接:https://pan.baidu.com/s/1bHvhk_42-IFAjNdjPPtMZw?pwd8888 提取码:8888 Python采集代码下载链接:采集代码.zip - 蓝奏云 学习知识费力气,收集整理更不易…...

【原创 附源码】Flutter海外登录--Tiktok登录最详细流程
最近接触了几个海外登录的平台,踩了很多坑,也总结了很多东西,决定记录下来给路过的兄弟坐个参考,也留着以后留着回顾。更新时间为2024年2月7日,后续集成方式可能会有变动,所以目前的集成流程仅供参考&#…...
)
国内chatGPT3.5升级到chatGPT4.0的教程(24年2月更新)
最新的充值方法看这里。 通过虚拟卡 WildCard 的方式来升级 GPT 4.0 最快了,大概2分钟就可以升级完成, 而且升级 GPT 4.0 价钱也不贵,虚拟卡一年10美元,GPT4 每个月也才 20美元。如果你觉得 GPT 4.0 对你可能有帮助,那就赶快来升级…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...

RLHF vs RLVR:对齐学习中的两种强化方式详解
在语言模型对齐(alignment)中,强化学习(RL)是一种重要的策略。而其中两种典型形式——RLHF(Reinforcement Learning with Human Feedback) 与 RLVR(Reinforcement Learning with Ver…...
