算法沉淀——位运算(leetcode真题剖析)

算法沉淀——位运算
- 常用位运算总结
- 1.基础位运算
- 2.确定一个数中第x位是0还是1
- 3.将一个数的第x位改成1
- 4.将一个数的第x位改成0
- 5.位图
- 6.提取一个数最右边的1
- 7.删掉一个数最右边的1
- 8.异或运算
- 9.基础例题
- 力扣题目讲解
- 01.面试题 01.01. 判定字符是否唯一
- 02.丢失的数字
- 03.两整数之和
- 04.只出现一次的数字 II
- 05.面试题 17.19. 消失的两个数字
常用位运算总结
1.基础位运算
-
按位与(&):对两个二进制数的对应位进行与运算,结果中的每一位都是两个数对应位上的位与操作的结果。
int result = a & b; -
按位或(|):对两个二进制数的对应位进行或运算,结果中的每一位都是两个数对应位上的位或操作的结果。
int result = a | b; -
按位异或(^):对两个二进制数的对应位进行异或运算,结果中的每一位都是两个数对应位上的位异或操作的结果。
int result = a ^ b; -
按位取反(~):对一个二进制数的每一位取反,即将0变为1,将1变为0。
int result = ~a; -
左移(<<):将一个二进制数的所有位向左移动指定的位数,右侧用0填充。
int result = a << 2; // 将a的二进制表示向左移动2位 -
右移(>>): 将一个二进制数的所有位向右移动指定的位数,左侧用符号位填充(对于有符号整数),无符号整数左侧用0填充。
int result = a >> 1; // 将a的二进制表示向右移动1位
2.确定一个数中第x位是0还是1
(n>>x)&1
n >> x:右移操作符将二进制表示的整数n向右移动x位。这意味着我们把整数n的二进制表示向右移动x位。(n >> x) & 1:与操作符&对两个二进制数的对应位进行与运算。在这里,对(n >> x)的结果与二进制数1进行与运算。- 如果
(n >> x)的二进制表示中第x位是1,与1进行与运算的结果是1。 - 如果
(n >> x)的二进制表示中第x位是0,与1进行与运算的结果是0。
- 如果
这是一种常见的技巧,特别是在位操作中,用于提取或测试一个特定位的值。
3.将一个数的第x位改成1
n|=(1<<x)
1 << x:左移操作符将二进制数1向左移动x位。这意味着我们在二进制数1的基础上,将其向左移动x位,从而在第x位设置为1,其它位为0。n |= (1 << x):按位或赋值操作符|=将n的二进制表示与(1 << x)的二进制表示进行按位或运算,并将结果存储回n。这样,n的第x位被设置为1,其它位保持不变。- 如果
n的第x位原本是0,进行按位或运算后仍然为1。 - 如果
n的第x位原本是1,进行按位或运算后仍然为1。
- 如果
4.将一个数的第x位改成0
n&=(~(1<<x))
1 << x:左移操作符将二进制数1向左移动x位。这意味着我们在二进制数1的基础上,将其向左移动x位,从而在第x位设置为1,其它位为0。~(1 << x):按位取反操作符~将(1 << x)的每一位取反,即将第x位由1变为0,其它位由0变为1。n &= (~(1 << x)):按位与赋值操作符&=将n的二进制表示与(~(1 << x))的二进制表示进行按位与运算,并将结果存储回n。这样,n的第x位被设置为0,其它位保持不变。- 如果
n的第x位原本是1,进行按位与运算后变为0。 - 如果
n的第x位原本是0,进行按位与运算后仍然为0。
- 如果
5.位图
- 基本概念:位图是一个由二进制位组成的数组,其中每一位都表示一个元素的存在或缺失。通常,每个元素都与位图中的一个二进制位相对应。
- 表示集合:位图主要用于表示集合,其中集合中的每个元素都有一个唯一的标识符,例如整数。如果集合中的元素存在,对应位置的位被设置为1;如果元素不存在,对应位置的位被设置为0。
- 节省空间:相比于其他数据结构,位图在存储上更加紧凑。一个位可以表示一个元素的存在与否,因此对于包含大量小范围整数的集合,位图可以显著减少存储空间的需求。
示例:
考虑一个集合 {1, 3, 5, 7, 9},对应的位图可能如下所示:
1 0 1 0 1 0 1 0 1 0
这表示集合中的元素存在,对应位置的位为1。通过位图,我们可以方便地进行快速的集合操作和检索。
具体可以看我之前写过的一篇博客
https://blog.csdn.net/kingxzq/article/details/133775093
6.提取一个数最右边的1
n&-n
- 计算
-n:在计算机中,负数通常以补码形式表示。-n可以通过将n的各位取反(按位取反)然后加1得到。也就是说,-n是n的按位取反再加1。 - 位与操作
n & -n:将n与-n进行按位与操作。这将保留n中最右边的1,而将其他位都置为0。
这个技巧的背后是,n 和 -n 在二进制表示中只有最右边的1是相同的,其他位都是相反的。因此,按位与操作会保留这个共同的最右边的1,其他位会被置零。
例如,如果 n 的二进制表示是 1011000,那么 -n 的二进制表示是 0101000,进行按位与操作后得到 0001000,即提取了 n 中最右边的1。
7.删掉一个数最右边的1
n&(n-1)
- 计算
n-1:将整数n减去1。这相当于将n的最右边的1变为0,并且将该1右侧的所有位都取反。 - 位与操作
n & (n-1):将n与n-1进行按位与操作。这将保留n中除了最右边的1之外的所有位。
通过这个操作,n 中最右边的1及其右侧的所有位都会被清零,而其他位保持不变。
例如,如果 n 的二进制表示是 1011000,那么 n-1 的二进制表示是 1010111,进行按位与操作后得到 1010000,即删除了 n 中最右边的1。
8.异或运算
-
a ^ 0 = a:任何数与0进行异或运算的结果都是它本身。这是因为异或运算的规则是,如果两个对应位的输入相同,则输出为0,如果不同,则输出为1。因此,一个数与0进行异或,对应的位都保持不变,结果就是这个数本身。
例如:
a = 1010,0 = 0000,则a ^ 0 = 1010。 -
a ^ a = 0:任何数与自己进行异或运算的结果都是0。这是因为对应位相同的情况下输出为0,而数与自己的对应位肯定相同,因此结果为0。
例如:
a = 1010,则a ^ a = 0000。 -
a ^ b ^ c = a ^ (b ^R c):异或运算满足结合律,即无论是如何加括号,得到的结果都是相同的。这是因为异或运算的结果取决于每一位的对应关系,而不受操作数的先后顺序影响。
例如:
a = 1010,b = 1100,c = 0110,则(a ^ b) ^ c = 0010,a ^ (b ^ c) = 0010。
9.基础例题
191. 位1的个数
338. 比特位计数
461. 汉明距离
136. 只出现一次的数字
260. 只出现一次的数字 III
力扣题目讲解
01.面试题 01.01. 判定字符是否唯一
题目链接:https://leetcode.cn/problems/is-unique-lcci/
实现一个算法,确定一个字符串 s 的所有字符是否全都不同。
示例 1:
输入: s = "leetcode"
输出: false
示例 2:
输入: s = "abc"
输出: true
限制:
0 <= len(s) <= 100s[i]仅包含小写字母- 如果你不使用额外的数据结构,会很加分。
思路
这里我们先想到的可能是哈希的思路,再进一步优化我们可以使用数组来模拟哈希,但还不是最优的解法,因为题目要求这里是只有小写字母,因此我们可以用一个整形利用位图思想来进行每一个比特位,所以这里我们只需要确定这个整形中的x位是0还是1,以及将第x位改成1,再进行判定即可。
代码
class Solution {
public:bool isUnique(string astr) {int n = astr.size(); // 获取字符串的长度int c = 0; // 使用一个整数c来表示出现过的字符情况for (int i = 0; i < n; ++i) {int t = 'z' - astr[i]; // 计算字符到 'z' 的距离if ((c >> t) & 1) {// 如果对应位为1,表示之前已经出现过相同的字符,返回falsereturn false;} else {// 否则将对应位设为1,表示该字符已经出现过c |= (1 << t);}}// 如果遍历完整个字符串,没有发现重复字符,返回truereturn true;}
};
解释:
c是一个整数,用来表示字符串中出现过的字符情况。这里用到了位运算,通过将某一位设为1来表示某个字符是否出现过。t计算了字符到 ‘z’ 的距离,目的是在整数c中的相应位置标记字符是否出现过。(c >> t) & 1判断c中对应位是否为1,如果为1,说明之前已经有相同的字符出现,返回false。c |= (1 << t)将对应位设为1,表示该字符已经出现过。
02.丢失的数字
题目链接:https://leetcode.cn/problems/missing-number/
给定一个包含 [0, n] 中 n 个数的数组 nums ,找出 [0, n] 这个范围内没有出现在数组中的那个数。
示例 1:
输入:nums = [3,0,1]
输出:2
解释:n = 3,因为有 3 个数字,所以所有的数字都在范围 [0,3] 内。2 是丢失的数字,因为它没有出现在 nums 中。
示例 2:
输入:nums = [0,1]
输出:2
解释:n = 2,因为有 2 个数字,所以所有的数字都在范围 [0,2] 内。2 是丢失的数字,因为它没有出现在 nums 中。
示例 3:
输入:nums = [9,6,4,2,3,5,7,0,1]
输出:8
解释:n = 9,因为有 9 个数字,所以所有的数字都在范围 [0,9] 内。8 是丢失的数字,因为它没有出现在 nums 中。
示例 4:
输入:nums = [0]
输出:1
解释:n = 1,因为有 1 个数字,所以所有的数字都在范围 [0,1] 内。1 是丢失的数字,因为它没有出现在 nums 中。
提示:
n == nums.length1 <= n <= 1040 <= nums[i] <= nnums中的所有数字都 独一无二
思路
同样我们这里可以使用哈希来进行标记,但显然是需要额外的空间,这里不使用额外空间还有其他的办法,比如使用高斯求和公式求出前n项和,再减去数组内数字的和,或者使用异或运算,我们使用先和数组中的每一个数异或,再和数组长度每一位异或,最终结果就是缺少的数
代码
class Solution {
public:int missingNumber(vector<int>& nums) {int n=nums.size(),ret=0;for(auto x:nums) ret^=x;for(int i=0;i<=n;++i) ret^=i;return ret;}
};
解释:
ret是用于保存异或结果的变量。- 第一次循环中,对数组中的所有元素进行异或运算,这样重复的元素会被抵消,最终剩下的就是缺失的数字。
- 第二次循环中,对数组的下标和数组中的元素进行异或运算,包括了所有可能的数字,因为数组的下标范围是 [0, n],所以最终异或的结果即为缺失的数字。
03.两整数之和
题目链接:https://leetcode.cn/problems/sum-of-two-integers/
给你两个整数 a 和 b ,不使用 运算符 + 和 - ,计算并返回两整数之和。
示例 1:
输入:a = 1, b = 2
输出:3
示例 2:
输入:a = 2, b = 3
输出:5
提示:
-1000 <= a, b <= 1000
思路
这里我们需要知道位运算中的一种思想,即无进位相加,详细看下面代码即可
代码
class Solution {
public:int getSum(int a, int b) {while (b) {int t = a ^ b; // 异或运算,得到无进位的和b = (a & b) << 1; // 与运算和左移1位,得到进位a = t; // 更新a为无进位和,继续循环}return a; // 当进位为0时,a即为最终的和}
};
解释:
a ^ b执行异或运算,得到无进位的和。(a & b) << 1执行与运算和左移1位,得到进位。因为只有在 a 和 b 的对应位都为1时,才会产生进位。a = t更新a为无进位和,继续循环,直到进位为0。
04.只出现一次的数字 II
题目链接:https://leetcode.cn/problems/single-number-ii/
给你一个整数数组 nums ,除某个元素仅出现 一次 外,其余每个元素都恰出现 **三次 。**请你找出并返回那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法且使用常数级空间来解决此问题。
示例 1:
输入:nums = [2,2,3,2]
输出:3
示例 2:
输入:nums = [0,1,0,1,0,1,99]
输出:99
提示:
1 <= nums.length <= 3 * 104-231 <= nums[i] <= 231 - 1nums中,除某个元素仅出现 一次 外,其余每个元素都恰出现 三次
思路
- 外层循环遍历32位整数的每一位。
- 内层循环遍历数组中的每个元素,统计在当前位上出现的次数。
- 对3取余,得到只出现一次的元素在当前位上的值。
- 将当前位上的值加到结果中。
代码
class Solution {
public:int singleNumber(vector<int>& nums) {int ret = 0;for (int i = 0; i < 32; ++i) {int sum = 0;for (auto x : nums) {// 统计数组中所有元素在当前位上的和if (x >> i & 1) {sum++;}}// 对3取余,得到只出现一次的元素在当前位上的值sum %= 3;// 将当前位上的值加到结果中if (sum) {ret |= 1 << i;}}return ret;}
};
05.面试题 17.19. 消失的两个数字
题目链接:https://leetcode.cn/problems/missing-two-lcci/
给定一个数组,包含从 1 到 N 所有的整数,但其中缺了两个数字。你能在 O(N) 时间内只用 O(1) 的空间找到它们吗?
以任意顺序返回这两个数字均可。
示例 1:
输入: [1]
输出: [2,3]
示例 2:
输入: [2,3]
输出: [1,4]
提示:
nums.length <= 30000
思路
主要是通过两次异或操作来找到缺失的两个数。
第一次异或操作:在第一次循环中,首先对数组中的所有元素和[0, n+2]范围内的所有数进行异或操作。这会得到一个结果 tmp,其中包含了两个缺失的数的异或值。由于异或的性质,重复的数都被抵消了,而缺失的两个数的位上的值则保留了下来。
找到不同的位:接着,通过循环找到 tmp 二进制表示中的一个为1的位,即找到两个缺失数的二进制表示中不同的位,用 diff 表示。
第二次异或操作:接下来,再次循环数组和[0, n+2]范围内的所有数,根据 diff 的值将它们分为两组。一组中这个位上为1,另一组中这个位上为0。这样就将问题转化为两个子问题,分别找出每组中缺失的数。
返回结果:最终返回的结果就是这两个缺失的数。将它们分别赋值给 a 和 b。
代码
class Solution {
public:vector<int> missingTwo(vector<int>& nums) {int tmp = 0;// 第一次异或,将数组中的所有元素和[0, n+2]范围内的所有数进行异或for (auto x : nums) {tmp ^= x;}for (int i = 0; i <= nums.size() + 2; ++i) {tmp ^= i;}int diff = 0;// 找到两个缺失数字的二进制表示中不同的位while (1) {if (tmp >> diff & 1) {break;}diff++;}int a = 0, b = 0;// 第二次异或,根据不同的位将数组分为两组for (auto x : nums) {if (x >> diff & 1) {a ^= x;} else {b ^= x;}}for (int i = 0; i <= nums.size() + 2; ++i) {if (i >> diff & 1) {a ^= i;} else {b ^= i;}}return {a, b};}
};
相关文章:

算法沉淀——位运算(leetcode真题剖析)
算法沉淀——位运算 常用位运算总结1.基础位运算2.确定一个数中第x位是0还是13.将一个数的第x位改成14.将一个数的第x位改成05.位图6.提取一个数最右边的17.删掉一个数最右边的18.异或运算9.基础例题 力扣题目讲解01.面试题 01.01. 判定字符是否唯一02.丢失的数字03.两整数之和…...
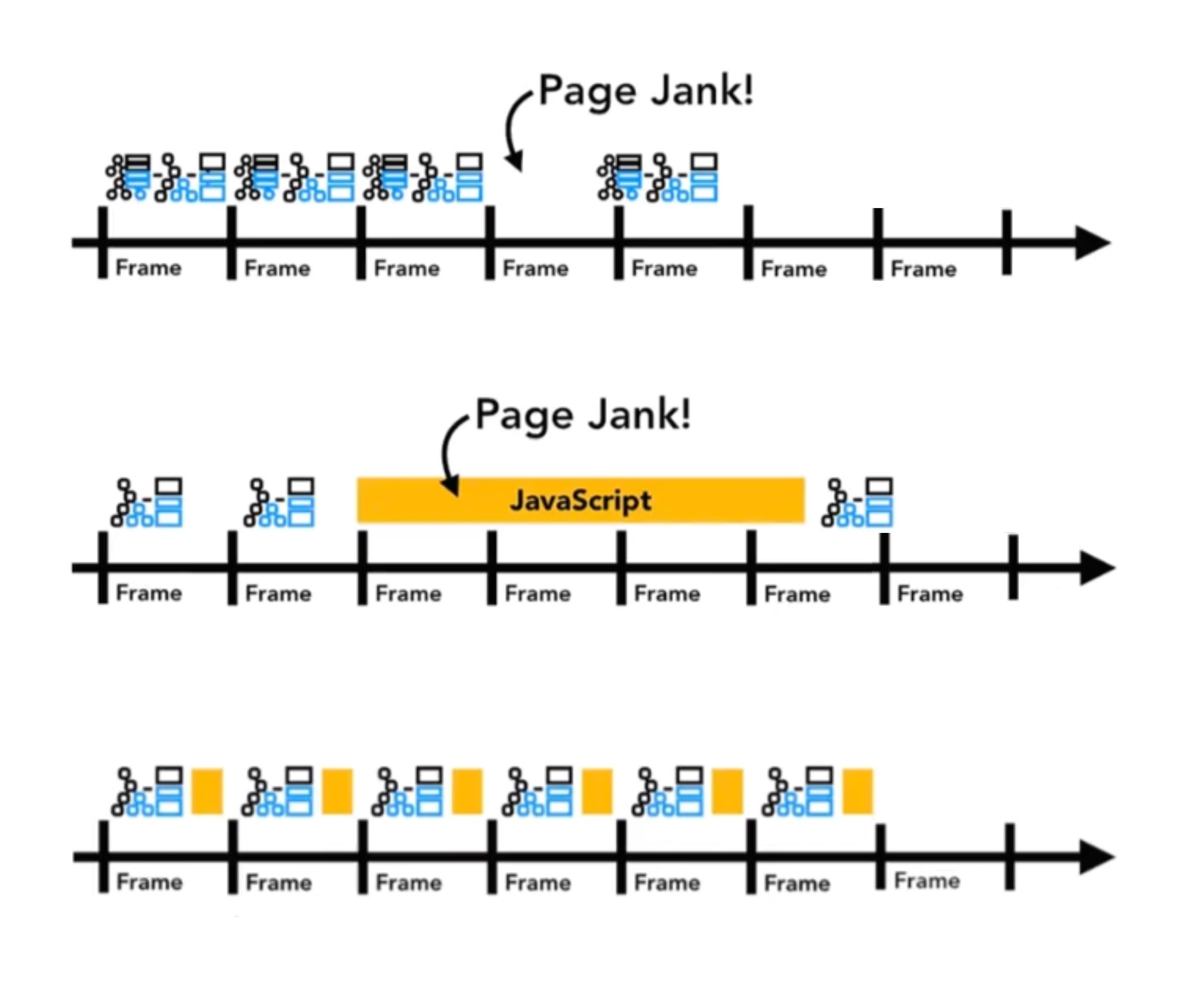
React18原理: 再聊Fiber架构下的时间分片
时间分片 react的任务可以被打断,其实就是基于时间分片的人眼最高能识别的帧数不超过30帧,电影的帧数差不多是在24浏览器的帧率一般来说是60帧,也就是每秒60个画面, 平均一个画面大概是16.5毫秒左右浏览器正常的工作流程是运算渲染ÿ…...

【玩转408数据结构】线性表——线性表的顺序表示(顺序表)
知识回顾 通过前文,我们了解到线性表是具有相同数据类型的有限个数据元素序列;并且,线性表只是一种逻辑结构,其不同存储形式所展现出的也略有不同,那么今天我们来了解一下线性表的顺序存储——顺序表。 顺序表的定义 …...

图像处理之《黑盒扰动的可逆噪声流鲁棒水印》论文阅读
一、文章摘要 近年来,基于深度学习的数字水印框架得到了广泛的研究。现有的方法大多采用基于“编码器-噪声层-解码器”的架构,其中嵌入和提取过程分别由编码器和解码器完成。然而,这种框架的一个潜在缺点是编码器和解码器可能不能很好地耦合…...

一个Vivado仿真问题的debug
我最近在看Synopsys的MPHY仿真代码,想以此为参考写个能实现PWM-G1功能的MPHY,并应用于ProFPGA原型验证平台。我从中抽取了一部分代码,用Vivado自带的仿真器进行仿真,然后就遇到了一个莫名其妙的问题,谨以此文作为debug…...

C#阿里云消息列队推送消息
推送消息到队列 IMNS nativeclient new Aliyun.MNS.MNSClient(accessKeyId, accessKeySecret, endpoint, _stsToken);var nativeSend nativeclient.GetNativeTopic("SMQ");nativeSend.PublishMessage("推送消息内容"); 需要引用Aliyun.MNS.dll 下载地址…...
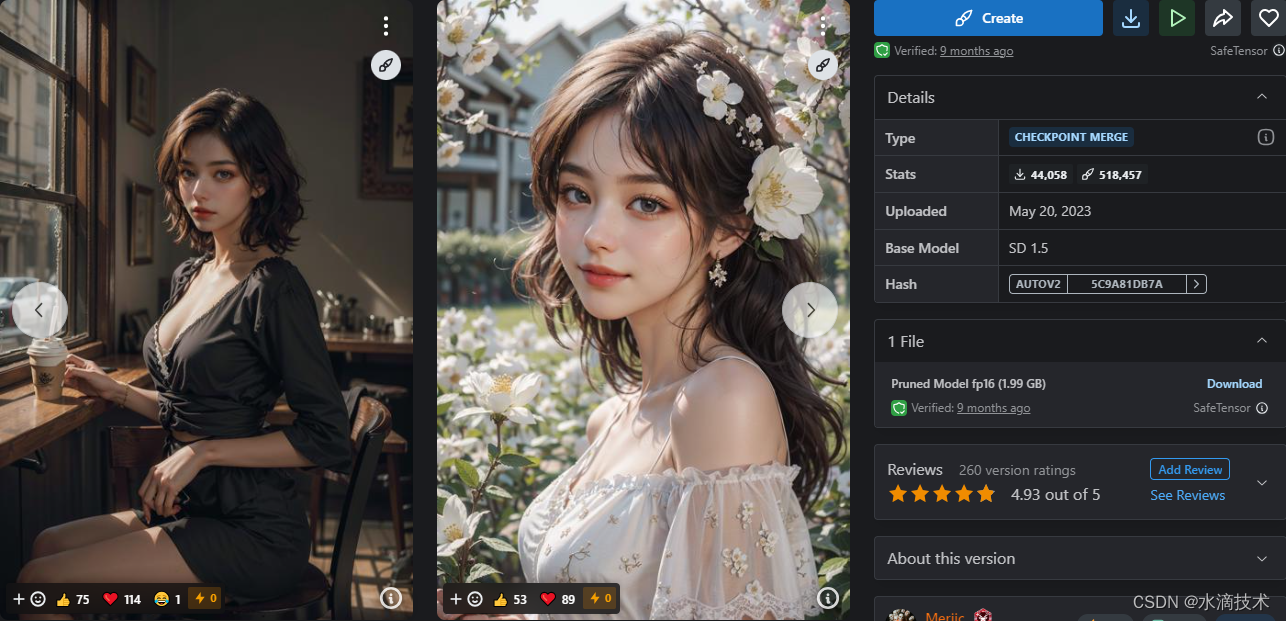
Stable Diffusion 模型下载:majicMIX sombre 麦橘唯美
本文收录于《AI绘画从入门到精通》专栏,专栏总目录:点这里。 文章目录 模型介绍生成案例案例一案例二案例三案例四案例五案例六案例七案例八案例九案例十...

WindowsLinuxmeterepreter渗透命令回顾
最近小编发现在学红队的时候总会忘记一些命令(基础的),导致整天红温,于是今天就来偷个懒记一下(一起回顾一下) 1.Linux 1.查看当前按目录 pwd2.查看文件内容 cat filename.txt3.cd 家族 cd ..|| cd ../…...
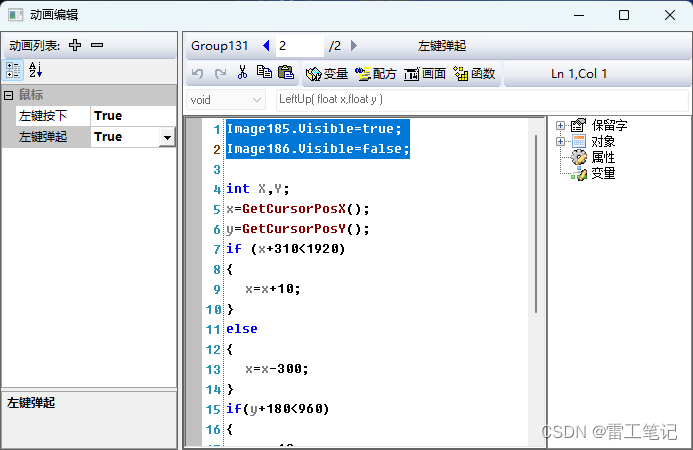
KingSCADA实现按钮点击效果
哈喽,你好啊,我是雷工! 在做SCADA项目的时候,按钮是不可缺少的功能,但软件自带的按钮太丑,已经无法满足现如今客户对界面美观度的要求。 这时候就需要UI小姐姐设计美观大气的SCADA界面,但UI设计…...

Python编程-二万字浅谈装饰器原理与装饰器设计模式和函数式编程案例讲解
Python编程-浅析装饰器原理与装饰器设计模式和函数式编程案例讲解 本文制作时基于Python3.11.8与Python3.12.1,存在谬误,请联系修改,希望对你有所帮助 什么是函数式编程 函数式编程(Functional Programming)是一种编程…...
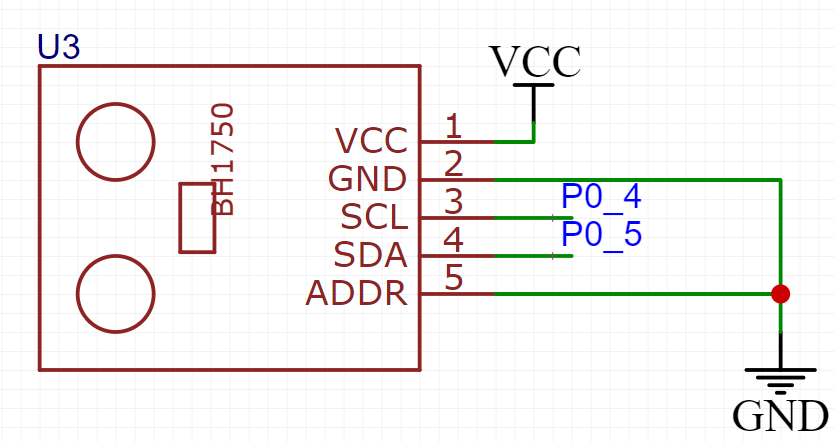
基于Zigbee的智能温室大棚系统(附详细使用教程+完整代码+原理图+完整课设报告)
🎊项目专栏:【Zigbee课程设计系列文章】(附详细使用教程+完整代码+原理图+完整课设报告) 前言 👑由于无线传感器网络(也即是Zigbee)作为🌐物联网工程的一门必修专业课,具有很强的实用性,因此很多院校都开设了zigbee的实训课程;👑同时最近很多使用了我的单片机课…...

【Web】Redis未授权访问漏洞学习笔记
目录 简介 靶机配置 Redis持久化 Redis动态修改配置 webshell 反弹shell Redis写入反弹shell任务 加固方案 简介 Redis(Remote Dictionary Server 远程字典服务器)是一个开源的内存数据库,也被称为数据结构服务器,它支持…...

【JAVA WEB】 css背景属性 圆角矩形的绘制
目录 背景属性设置 圆角矩形 背景属性设置 背景颜色,在style中 background-color:颜色; 背景图片 background-image:url(……) 背景图片的平铺方式 background-repeat: 平铺方式 repeat 平铺(默认)no-repeat 不平铺repeat-x 水平平铺repea…...
Docker-现代化应用部署的利器
一、容器部署的发展 今天我们来说说容器部署。我们知道容器部署的发展大致分三个阶段,下面来介绍一下不同阶段的部署方式的优缺点 物理机部署 优点是可以提供更高的性能、资源控制,也可以提供更好的数据隔离和安全性,因为不同的应用程序运行在…...

「优选算法」:山脉数组的峰顶索引
一、题目 符合下列属性的数组 arr 称为 山脉数组 : arr.length > 3存在 i(0 < i < arr.length - 1)使得: arr[0] < arr[1] < ... arr[i-1] < arr[i] arr[i] > arr[i1] > ... > arr[arr.length - 1] …...

网络安全红队基础建设与介绍
1.ATT&CK相关背景 ATT&CK在各种日常环境中都很有价值。开展任何防御活动时,可以应用ATT&CK防御法,参考攻击者及其行为。ATT&CK不仅对网络防御者提供通用技术库,还为渗透测试和红队提供了基础。提到对抗行为时,这为…...

Java语法学习反射
Java语法学习反射 大纲 基本介绍class的介绍 具体案例 1. 基本介绍 流程图(程序在计算机的阶段) 反射的主要的类 这个提高效率不大 2. class的介绍 对于第三点:首先类只会加载一次,得到的class的对象,也只有一…...

【MySQL】操作库 —— 库的操作 -- 详解
一、增删数据库 1、创建数据库 create database db_name; 本质就是在 /var/lib/mysql 创建一个目录。 说明: 大写的表示关键字。[ ] 是可选项。CHARACTER SET:指定数据库采用的字符集。COLLATE:指定数据库字符集的校验规则。 2、数据库删除…...

Rust安装——Win10
安装步骤 1、下载RUSTUP-INIT.EXE(64-BIT) 2、由于国外源下载依赖太慢,因此建议增加win10环境变量配置国内源,增加RUSTUP_DIST_SERVER、RUSTUP_UPDATE_ROOT环境变量即可 RUSTUP_DIST_SERVER随便选择其中的一个源就行,…...

【教学类-46-07】20240212立体春字1.0
背景需求: 在南浔古镇的非遗文化馆里看到一个新年活动折纸——立体春字, 我记得这个就是一个双三角结构折纸,完全可以用15*15的手工纸给孩子们做一套。 折纸教程 双三角折法 【“鼠”你有才】纸艺教学 剪纸——立体春字(2月23日…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...
