题解19-24
48. 旋转图像 - 力扣(LeetCode)
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在** 原地** 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1:
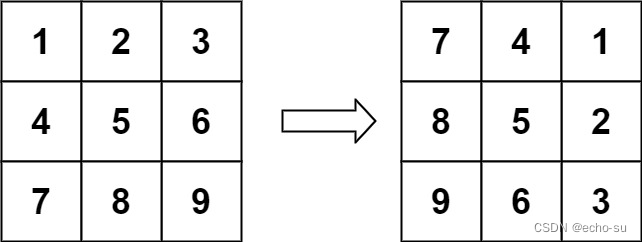
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[[7,4,1],[8,5,2],[9,6,3]]
示例 2:
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
提示:
n == matrix.length == matrix[i].length1 <= n <= 20-1000 <= matrix[i][j] <= 1000
思路:
这道题的思路我们可以总结为两个步骤,可以手写一个看看
- 将矩阵绕着对角线交换元素
- 按照中间的那条线交换
class Solution {
public:void rotate(vector<vector<int>>& matrix) {int n = matrix.size();for(int i = 0; i < n; i ++){for(int j = i + 1; j < n; j ++)swap(matrix[i][j], matrix[j][i]);}for(int i = 0; i < n; i ++){for(int j = 0, k = n - 1; j < k; j ++, k --){swap(matrix[i][j], matrix[i][k]);}}}
};
49. 字母异位词分组 - 力扣(LeetCode)
给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。
字母异位词 是由重新排列源单词的所有字母得到的一个新单词。
示例 1:
输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
输出: [["bat"],["nat","tan"],["ate","eat","tea"]]
示例 2:
输入: strs = [""]
输出: [[""]]
示例 3:
输入: strs = ["a"]
输出: [["a"]]
提示:
1 <= strs.length <= 1040 <= strs[i].length <= 100strs[i]仅包含小写字母
思路:
这道题就是用先排序,然后用哈希表记录对应下标即可
class Solution {
public:vector<vector<string>> groupAnagrams(vector<string>& strs) {map<string, vector<int>> pos;for(int i = 0; i < strs.size(); i ++){string s = strs[i];sort(s.begin(), s.end());pos[s].push_back(i);}vector<vector<string>> ans;for(auto&[k, v] : pos){vector<string> temp;for(auto&c : v)temp.push_back(strs[c]);ans.push_back(temp);}return ans;}
};
53. 最大子数组和 - 力扣(LeetCode)
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1]
输出:1
示例 3:
输入:nums = [5,4,-1,7,8]
输出:23
提示:
1 <= nums.length <= 105-104 <= nums[i] <= 104
**进阶:**如果你已经实现复杂度为 O(n) 的解法,尝试使用更为精妙的 分治法 求解。
思路:
这道题可以用动态规划思路来实现,我们假设 f [ i ] f[i] f[i]表示下标为i的最大值,所以 f [ i ] f[i] f[i]可以由 m a x ( f [ i − 1 ] + n u m s [ i ] , n u m s [ i ] ) max(f[i - 1] + nums[i], nums[i]) max(f[i−1]+nums[i],nums[i])转移得到
class Solution {
public:int maxSubArray(vector<int>& nums) {int n = nums.size();vector<int> f(n + 1, 0);f[0] = nums[0];int res = nums[0];for(int i = 1; i < n; i ++){f[i] = max(f[i - 1] + nums[i], nums[i]);res = max(res, f[i]);}return res;}
};
55. 跳跃游戏 - 力扣(LeetCode)
给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。
示例 1:
输入:nums = [2,3,1,1,4]
输出:true
解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2:
输入:nums = [3,2,1,0,4]
输出:false
解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
提示:
1 <= nums.length <= 1040 <= nums[i] <= 105
思路:
我们能够跳到的肯定是连续的一段,所以我们只需要统计每一个点跳到最远的位置即可
class Solution {
public:bool canJump(vector<int>& nums) {for (int i = 0, j = 0; i < nums.size(); i ++ ) {if (j < i) return false;j = max(j, i + nums[i]);//}return true;}
};
56. 合并区间 - 力扣(LeetCode)
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]]
输出:[[1,6],[8,10],[15,18]]
解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入:intervals = [[1,4],[4,5]]
输出:[[1,5]]
解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
提示:
1 <= intervals.length <= 104intervals[i].length == 20 <= starti <= endi <= 104
思路:
将所有区间按照左端点进行排序,然后遍历所有区间,如果新加入的区间左端点比当前区间的右端点还要大,即没有交集,我们就记录一个答案,并且更新新的左端点和右端点,最后不要忘记统计最后一个左端点和右端点
class Solution {
public:vector<vector<int>> merge(vector<vector<int>>& intervals) {vector<vector<int>> res;int n = intervals.size();if(n == 0) return res;sort(intervals.begin(), intervals.end());int l = intervals[0][0], r = intervals[0][1];for(int i = 1; i < n; i ++){if(intervals[i][0] > r){res.push_back({l, r});l = intervals[i][0], r = intervals[i][1];}else{r = max(r, intervals[i][1]);}}res.push_back({l, r});return res;}
};
62. 不同路径 - 力扣(LeetCode)
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
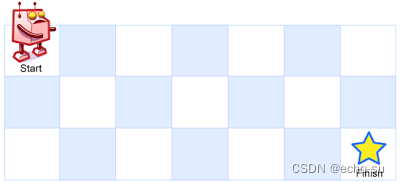
输入:m = 3, n = 7
输出:28
示例 2:
输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下
示例 3:
输入:m = 7, n = 3
输出:28
示例 4:
输入:m = 3, n = 3
输出:6
提示:
1 <= m, n <= 100- 题目数据保证答案小于等于
2 * 109
思路:
这道题也是经典的动态规划题目,每个点只能够从左边和上边转移过来,也是可以用记忆化搜索实现的
class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m, vector<int>(n, 0));for(int i = 0; i < m; i ++){dp[i][0] = 1;}for(int i = 0; i < n; i ++){dp[0][i] = 1;}for(int i = 1; i < m; i ++){for(int j = 1; j < n; j ++){dp[i][j] = dp[i][j - 1] + dp[i - 1][j];}}// return 0;return dp[m - 1][n - 1];}
};
class Solution {
public:vector<vector<int>> memo;int dfs(int x, int y){if(x == 0 || y == 0)return memo[x][y] = 1;if(memo[x][y] != 0)return memo[x][y];return memo[x][y] = dfs(x - 1, y) + dfs(x, y - 1);}int uniquePaths(int m, int n) {if(m <= 0 || n <= 0)return 0;memo = vector<vector<int>>(m, vector<int>(n, 0));return dfs(m - 1, n - 1);}
};
相关文章:

题解19-24
48. 旋转图像 - 力扣(LeetCode) 给定一个 n n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。 你必须在** 原地** 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。 示例 1࿱…...

基于图像掩膜和深度学习的花生豆分拣(附源码)
目录 项目介绍 图像分类网络构建 处理花生豆图片完成预测 项目介绍 这是一个使用图像掩膜技术和深度学习技术实现的一个花生豆分拣系统 我们有大量的花生豆图片,并以及打好了标签,可以看一下目录结构和几张具体的图片 同时我们也有几张大的图片&…...
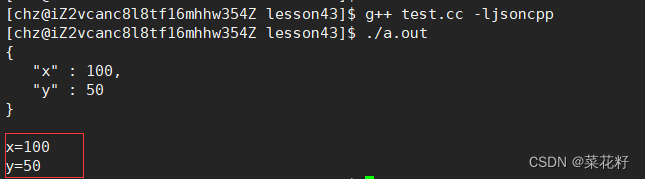
【网络】:序列化和反序列化
序列化和反序列化 一.json库 二.简单使用json库 前面已经讲过TCP和UDP,也写过代码能够进行双方的通信了,那么有没有可能这种通信是不安全的呢?如果直接通信,可能会被底层捕捉;可能由于网络问题,一方只接收到…...
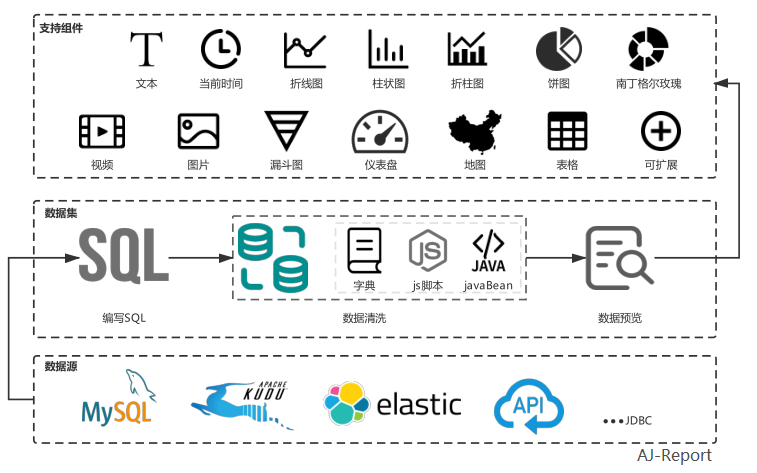
AJ-Report 【开源的一个BI平台】
AJ-Report是全开源的一个BI平台,酷炫大屏展示,能随时随地掌控业务动态,让每个决策都有数据支撑。 多数据源支持,内置mysql、elasticsearch、kudu驱动,支持自定义数据集省去数据接口开发,目前已支持30…...

Matplotlib核心:掌握Figure与Axes
详细介绍Figure和Axes(基于Matplotlib) 🌵文章目录🌵 🌳引言🌳🌳 一、Figure(图形)🌳🍁1. 创建Figure🍁🍁2. 添加Axes&am…...
问题:A注册会计师必须在期中实施实质性程序的情形是()。 #学习方法#其他
问题:A注册会计师必须在期中实施实质性程序的情形是()。 A.甲公司整体控制环境不佳 B.将期中实质性程序所获证据与期末数据进行比较 C.评估的认定层次重大错报风险很高 D.没有把握通过在期中…...
)
C#系列-C#EF框架返回单行记录(24)
在C#中,使用Entity Framework (EF)框架时,如果你想要执行一个查询并返回单行记录,你可以使用SingleOrDefault、FirstOrDefault、Single或First方法。这些方法适用于DbSet<T>对象,它们可以执行查询并返回单个实体或默认值&am…...
的生成)
【PyTorch】张量(Tensor)的生成
PyTorch深度学习总结 第一章 Pytorch中张量(Tensor)的生成 文章目录 PyTorch深度学习总结一、什么是PyTorch?二、张量(Tensor)1、张量的数据类型2、张量生成和信息获取 总结 一、什么是PyTorch? PyTorch是一个开源的深度学习框架,基于Python…...
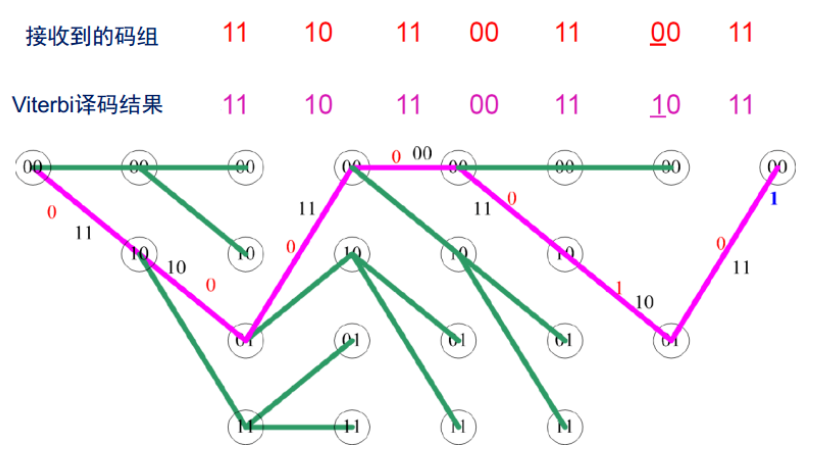
【5G NR】【一文读懂系列】移动通讯中使用的信道编解码技术-Viterbi译码原理
目录 一、引言 二、Viterbi译码的基本原理 2.1 卷积码与网格图 2.2 Viterbi算法的核心思想 2.3 路径度量与状态转移 三、Viterbi译码算法工作原理详解 3.1 算法流程 3.2 关键步骤 3.3 译码算法举例 3.4 性能特点 四、Viterbi译码的应用场景 4.1 移动通信系统 4.2 卫…...

矩阵在计算机图像处理中的应用
矩阵在计算机图像处理中是非常核心的概念,因为它们为表示和操作图像数据提供了一种非常方便和强大的方式。以下是矩阵在计算机图像处理中的一些关键作用: 图像表示:在计算机中,图像通常被表示为像素矩阵,也就是二维数组…...

Java实现教学资源共享平台 JAVA+Vue+SpringBoot+MySQL
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 数据中心模块2.2 课程档案模块2.3 课程资源模块2.4 课程作业模块2.5 课程评价模块 三、系统设计3.1 用例设计3.2 类图设计3.3 数据库设计3.3.1 课程档案表3.3.2 课程资源表3.3.3 课程作业表3.3.4 课程评价表 四、系统展…...
:使用 ant.jar 执行 SQL 脚本文件)
Spring Boot(六十五):使用 ant.jar 执行 SQL 脚本文件
ant用处,主要用在编译java文件,打包,部署。打包:jar,war,ear包等。ant在项目中有很重要的作用。今天我们讲解它的另一个作用:执行 SQL 脚本文件。 1 引入依赖 <dependency><groupId>org.apache.ant</groupId><artifactId>ant</artifactId&g…...
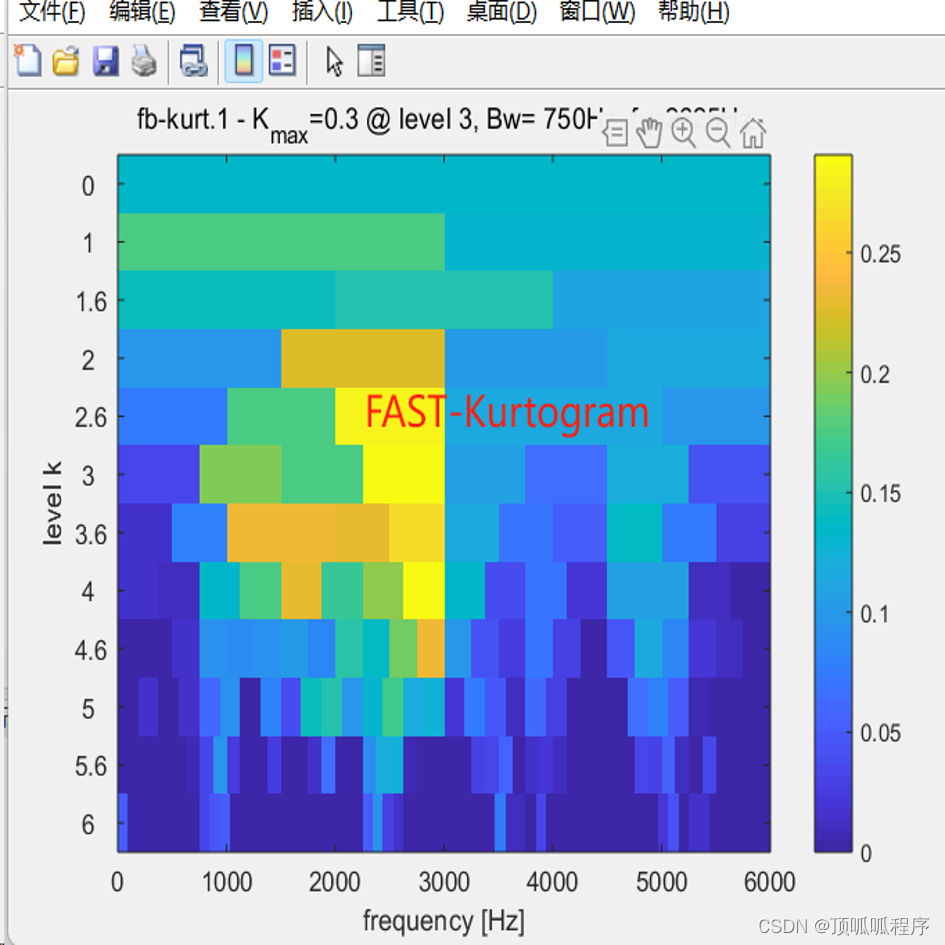
161基于matlab的快速谱峭度方法
基于matlab的快速谱峭度方法,选择信号峭度最大的频段进行滤波,对滤波好信号进行包络谱分析。输出快速谱峭度及包络谱结果。程序已调通,可直接运行。 161 信号处理 快速谱峭度 包络谱分析 (xiaohongshu.com)...
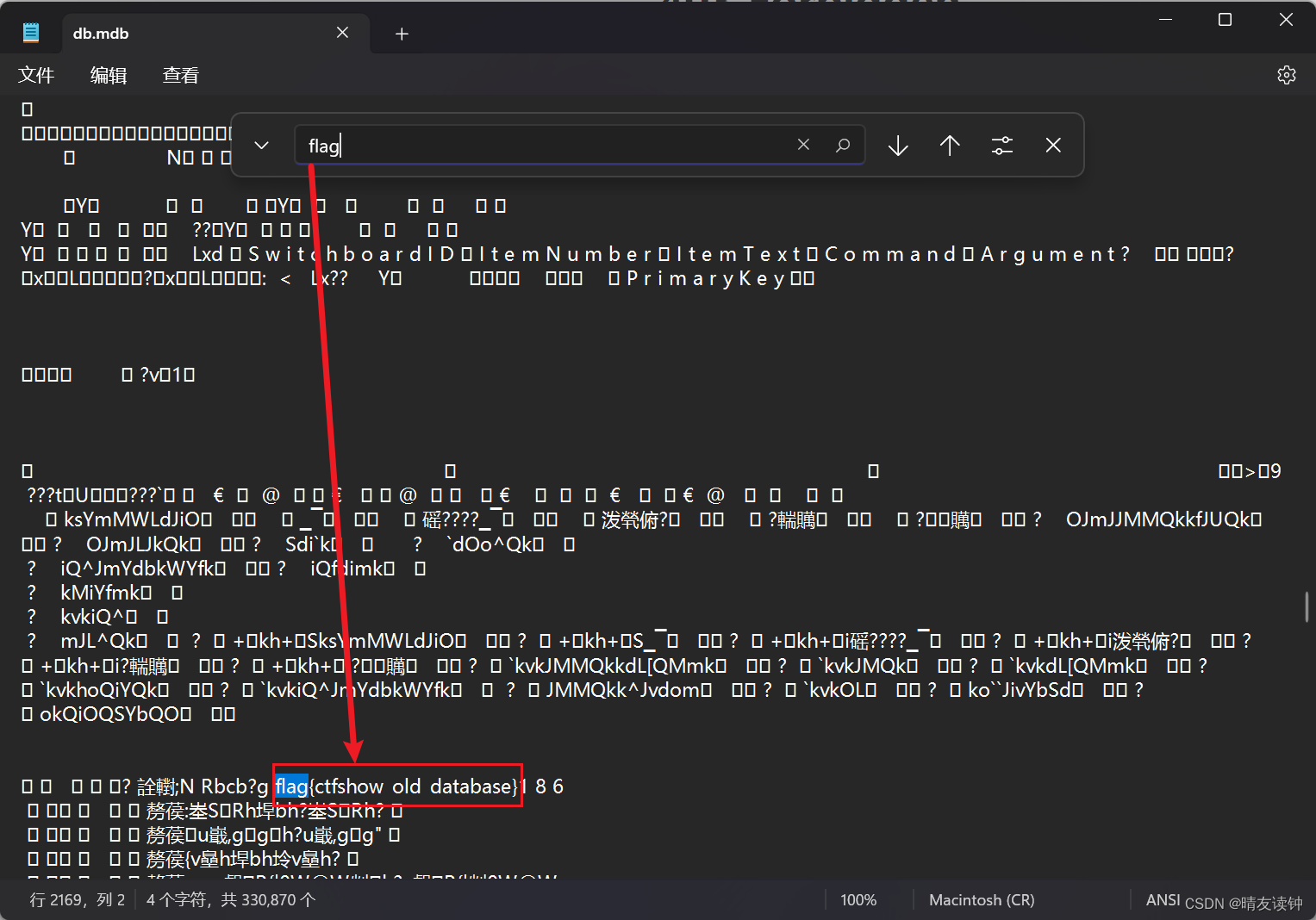
CTFshow-WEB入门-信息搜集
web1(查看注释1) wp 右键查看源代码即可找到flag web2(查看注释2) wp 【CtrlU】快捷键查看源代码即可找到flag web3(抓包与重发包) wp 抓包后重新发包,在响应包中找到flag web4(robo…...
)
django密码管理器(创建项目)
目录 创建项目 安装django 创建项目(django-admin) 创建管理员用户 创建数据库 创建项目 新建一个项目文件夹,如"密码管理器" 安装django 要先安装pip,pip安装地址:pypi.org、pypi.python.org、cheeseshop.python.org pip install django 创建项…...

Centos7之Oracle12c安装与远程连接配置
Centos7之Oracle12c安装与远程连接配置 文章目录 Centos7之Oracle12c安装与远程连接配置1.Oracle官网2. Centos7中安装Oracle12c(12.2.0.1.0)2.1 Introduction (介绍)2.2 Prerequisites(先决条件)2.3 Installation Steps(安装步骤)2.4 Oracle Installer Screens(Oracle安装程序…...
CVE-2022-25578 漏洞复现
CVE-2022-25578 路由/admin/admin.php是后台,登录账号和密码默认是admin、tao,选择文件管理。 是否还记得文件上传中的.htaccess配置文件绕过发,在这个文件中加入一句AddType application/x-httpd-php .jpg,将所有jpg文件当作php…...
)
Ubuntu22.04安装黑屏(进入U盘安装引导时 和 安装完成后)
一:进入U盘安转引导时黑屏 问题描述:选择’try or install ubuntu’,开始安装,出现黑屏。 解决方法:(可行) 安装时,先选择" try or install ubuntu", 此时不要按enter&a…...
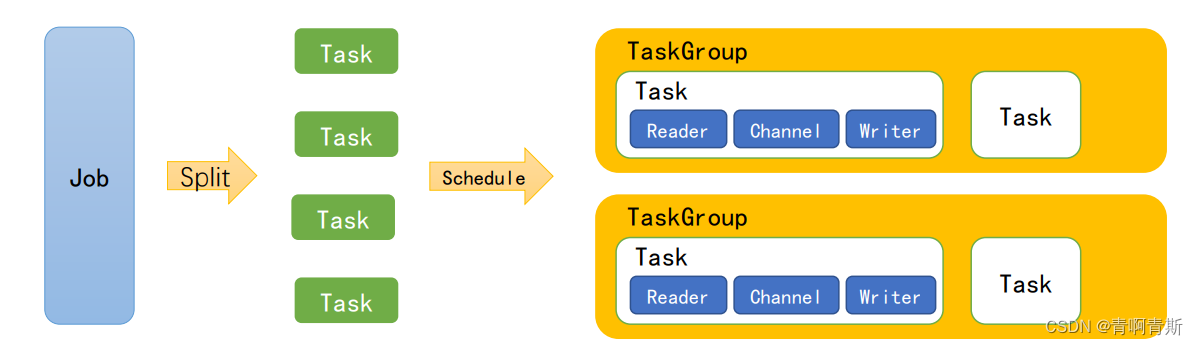
一、DataX简介
DataX简介 一、什么是DataX二、DataX设计三、支持的数据源四、框架设计五、运行原理六、DataX和Sqoop对比 一、什么是DataX DataX是阿里巴巴开源的一个异构数据源离线同步工具,致力于实现包括关系型数据库(MySQL、Oracle等)、HDFS、Hive、OD…...

直播app开发,技术驱动的实时互动新纪元
随着互联网技术的快速发展,直播已成为我们日常生活的重要组成部分。从娱乐、教育到商业活动,直播的广泛应用正在改变着我们的生活和工作方式。在这一变革中,直播开发扮演着至关重要的角色。本文将探讨直播开发的核心理念、技术挑战以及未来的…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...
