每日OJ题_位运算⑤_力扣371. 两整数之和
目录
力扣371. 两整数之和
解析代码
力扣371. 两整数之和
371. 两整数之和
难度 简单
给你两个整数 a 和 b ,不使用 运算符 + 和 - ,计算并返回两整数之和。
示例 1:
输入:a = 1, b = 2 输出:3
示例 2:
输入:a = 2, b = 3 输出:5
提示:
-1000 <= a, b <= 1000
class Solution {
public:int getSum(int a, int b) {}
};解析代码
此题知识点就是异或运算为无进位相加,异或后想办法找到进位就行了,进位就是两个数按位与然后左移一位,重复相加至进位为0即为答案。
class Solution {
public:int getSum(int a, int b) {while (b != 0){unsigned int carry = (unsigned int)(a & b) << 1; // 进位a = a ^ b; // 无进位相加b = carry; // 进位不为0的话就一直加,如a已经是a^b的结果,再^b,加进位}return a;}
};相关文章:

每日OJ题_位运算⑤_力扣371. 两整数之和
目录 力扣371. 两整数之和 解析代码 力扣371. 两整数之和 371. 两整数之和 难度 简单 给你两个整数 a 和 b ,不使用 运算符 和 - ,计算并返回两整数之和。 示例 1: 输入:a 1, b 2 输出:3示例 2: …...

Mysql中索引优化和失效
什么是索引 要了解索引优化和索引失效的场景就要先了解什么是索引 索引是一种有序的存储结构,按照单个或者多个列的值进行排序,以提升搜索效率。 索引的类型 UNIQUE唯一索引 不可以出现相同的值,可以有NULL值。 INDEX普通索引 允许出现相同…...

使用Python+OpenCV2进行图片中的文字分割(支持竖版)
扣字和分割 把图片中的文字,识别出来,并将每个字的图片抠出来; import cv2 import numpy as npHIOG 50 VIOG 3 Position []水平投影 def getHProjection(image):hProjection np.zeros(image.shape,np.uint8)# 获取图像大小(h,w)image.sh…...
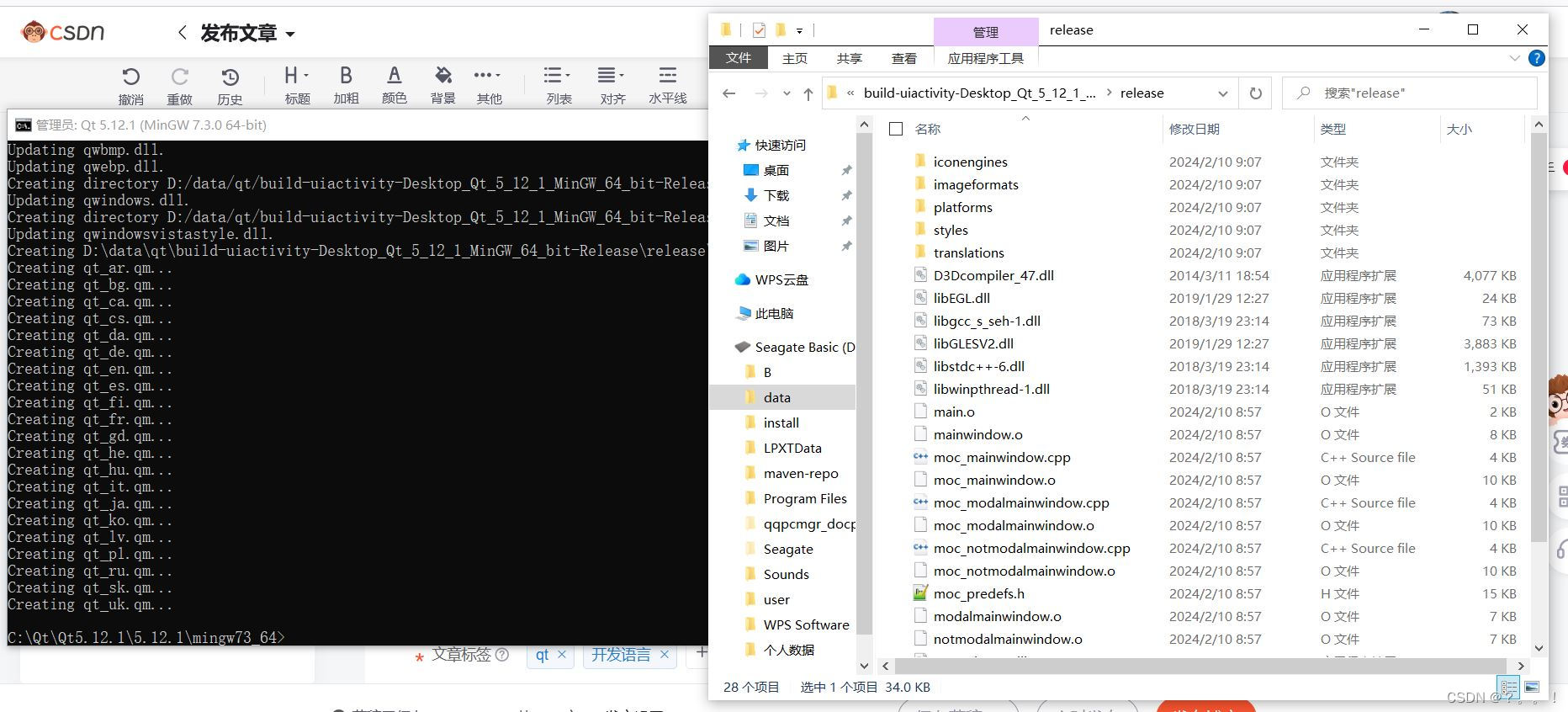
Qt中程序发布及常见问题
1、引言 当我们写好一个程序时通常需要发布给用户使用,那么在Qt中程序又是如何实现发布的呢,这里我就来浅谈一下qt中如何发布程序,以及发布程序时的常见问题。 2、发布过程 2.1、切换为release模式 当我们写qt程序时默认是debug模式&#x…...

C语言第二十三弹---指针(七)
✨个人主页: 熬夜学编程的小林 💗系列专栏: 【C语言详解】 【数据结构详解】 指针 1、sizeof和strlen的对比 1.1、sizeof 1.2、strlen 1.3、sizeof 和 strlen的对比 2、数组和指针笔试题解析 2.1、⼀维数组 2.2、二维数组 总结 1、si…...
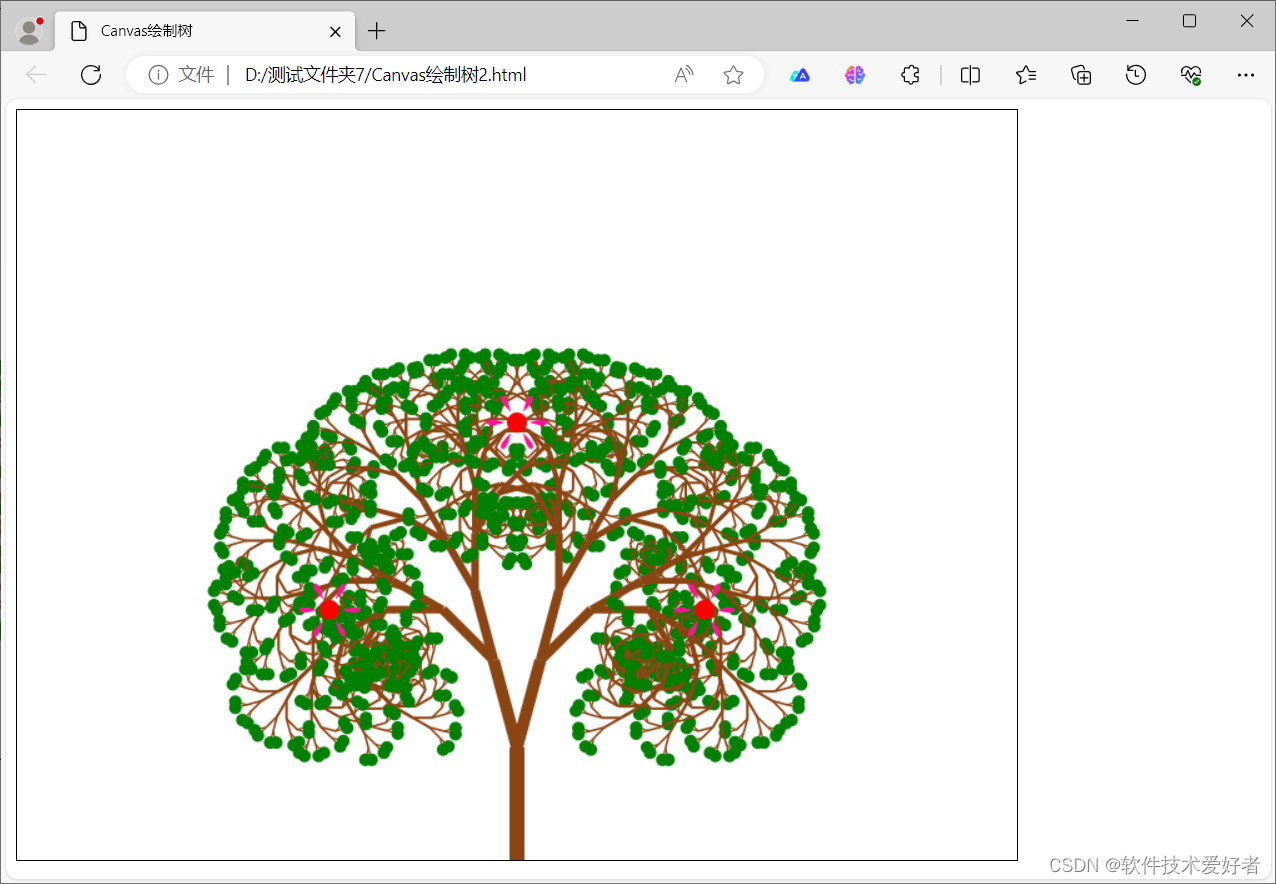
用HTML5 + JavaScript绘制花、树
用HTML5 JavaScript绘制花、树 <canvas>是一个可以使用脚本 (通常为JavaScript) 来绘制图形的 HTML 元素。 <canvas> 标签/元素只是图形容器,必须使用脚本来绘制图形。 HTML5 canvas 图形标签基础https://blog.csdn.net/cnds123/article/details/112…...

Science重磅_让大模型像婴儿一样学习语言
英文名称: Grounded language acquisition through the eyes and ears of a single child 中文名称: 通过一个孩子的眼睛和耳朵基于实践学习语言 文章: https://www.science.org/doi/10.1126/science.adi1374 代码: https://github.com/wkvong/multimodalbaby 作者: Wai Keen V…...
Java 数据结构篇-实现红黑树的核心方法
🔥博客主页: 【小扳_-CSDN博客】 ❤感谢大家点赞👍收藏⭐评论✍ 文章目录 1.0 红黑树的说明 2.0 红黑树的特性 3.0 红黑树的成员变量及其构造方法 4.0 实现红黑树的核心方法 4.1 红黑树内部类的核心方法 (1)判断当前…...
【实战】一、Jest 前端自动化测试框架基础入门(中) —— 前端要学的测试课 从Jest入门到TDD BDD双实战(二)
文章目录 一、Jest 前端自动化测试框架基础入门5.Jest 中的匹配器toBe 匹配器toEqual匹配器toBeNull匹配器toBeUndefined匹配器和toBeDefined匹配器toBeTruthy匹配器toBeFalsy匹配器数字相关的匹配器字符串相关的匹配器数组相关的匹配器异常情况的匹配器 6.Jest 命令行工具的使…...

【C语言 - 力扣 - 反转链表】
反转链表题目描述 给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。 题解1-迭代 假设链表为 1→2→3→∅,我们想要把它改成 ∅←1←2←3。 在遍历链表时,将当前节点的 next 指针改为指向前一个节点。由于节点没…...
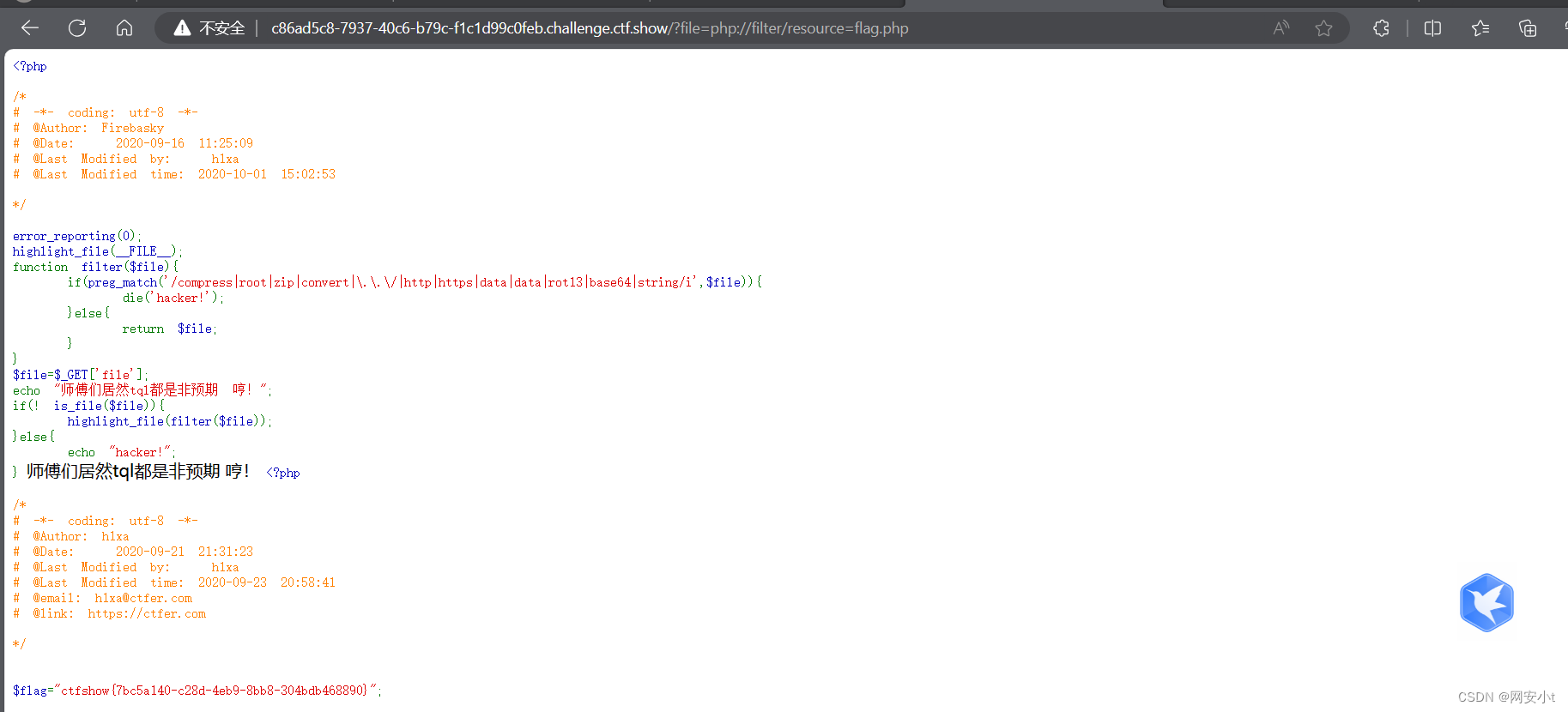
ctfshow-php特性(web102-web115)
目录 web102 web103 web104 web105 web106 web107 web108 web109 web110 web111 web112 web113 web114 web115 实践是检验真理的 要多多尝试 web102 <?php highlight_file(__FILE__); $v1$_POST[V1]; $v2$_GET[v2]; $v3$_GET[v3]; $v4is_numeric($v2)and is…...

python系统学习Day1
section1 python introduction 文中tips只做拓展,可跳过。 PartOne introduction 首先要对于python这门语言有一个宏观的认识,包括特点和应用场景。 特点分析: 优势 提供了完善的基础代码库,许多功能不必从零编写简单优雅 劣势 运…...

Idea里自定义封装数据警告解决 Spring Boot Configuration Annotation Processor not configured
我们自定对象封装指定数据,封装类上面一个红色警告,虽然不影响我们的执行,但是有强迫症看着不舒服, 去除方式: 在pom文件加上坐标刷新 <dependency><groupId>org.springframework.boot</groupId><…...

【流程图——讲解】
流程图介绍 流程图介绍 流程图介绍 流程图是一种图表,它展示了工作流程或过程中的步骤顺序,它通常由不同的符号表示,每个符号都代表一个步骤或过程中的一个元素,流程图非常有用,因为它们可以提供清晰、视觉化的过程表…...

「计算机网络」物理层
物理层的基本概念 物理层的作用:尽可能屏蔽掉不同传输媒体和通信手段的差异物理层规程:用于物理层的协议主要任务:确定与传输媒体的接口有关的一些特性 机械特性电器特性功能特性过程特性 数据通信的基础知识 数据通信系统的模型 划分为…...

ARM与X86架构的区别与联系
文章目录 1.什么是CPU2.复杂指令集和精简指令集3.ARM架构与X86架构的比较3.1.制造工艺3.2 64位计算3.3 异构计算3.4 功耗 4.ARM和X86的发展现状Reference 1.什么是CPU 中央处理单元(CPU)主要由运算器、控制器、寄存器三部分组成,从字面意思看…...

蓝桥杯每日一题------背包问题(二)
前言 本次讲解背包问题的一些延申问题,新的知识点主要涉及到二进制优化,单调队列优化DP,树形DP等。 多重背包 原始做法 多重背包的题意处在01背包和完全背包之间,因为对于每一个物品它规定了可选的个数,那么可以考虑…...

牛客错题整理——C语言(实时更新)
1.以下程序的运行结果是() #include <stdio.h> int main() { int sum, pad,pAd; sum pad 5; pAd sum, pAd, pad; printf("%d\n",pAd); }答案为7 由于赋值运算符的优先级高于逗号表达式,因此pAd sum, pAd, pad;等价于(…...

CIFAR-10数据集详析:使用卷积神经网络训练图像分类模型
1.数据集介绍 CIFAR-10 数据集由 10 个类的 60000 张 32x32 彩色图像组成,每类 6000 张图像。有 50000 张训练图像和 10000 张测试图像。 数据集分为5个训练批次和1个测试批次,每个批次有10000张图像。测试批次正好包含从每个类中随机选择的 1000 张图像…...

《傲剑狂刀》中的人物性格——龙吟风
在《傲剑狂刀》这款经典武侠题材的格斗游戏中,龙吟风作为一位具有传奇色彩的角色,其性格特征复杂且引人入胜。以下是对龙吟风这一角色的性格特点进行深度剖析: 一、孤高独立的剑客气质 龙吟风的名字本身就流露出一种独特的江湖气息,"吟风"象征着他的飘逸与淡泊名…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...
