「优选算法刷题」:寻找旋转排序数组中的最小值
一、题目
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:
- 若旋转
4次,则可以得到[4,5,6,7,0,1,2] - 若旋转
7次,则可以得到[0,1,2,4,5,6,7]
注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [3,4,5,1,2] 输出:1 解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。
示例 2:
输入:nums = [4,5,6,7,0,1,2] 输出:0 解释:原数组为 [0,1,2,4,5,6,7] ,旋转 3 次得到输入数组。
示例 3:
输入:nums = [11,13,15,17] 输出:11 解释:原数组为 [11,13,15,17] ,旋转 4 次得到输入数组。
二、思路解析
观察一下题目所给的数据,比如示例 1 ,我们可以发现下标为 3 的元素 1 跟其他元素有所不同:
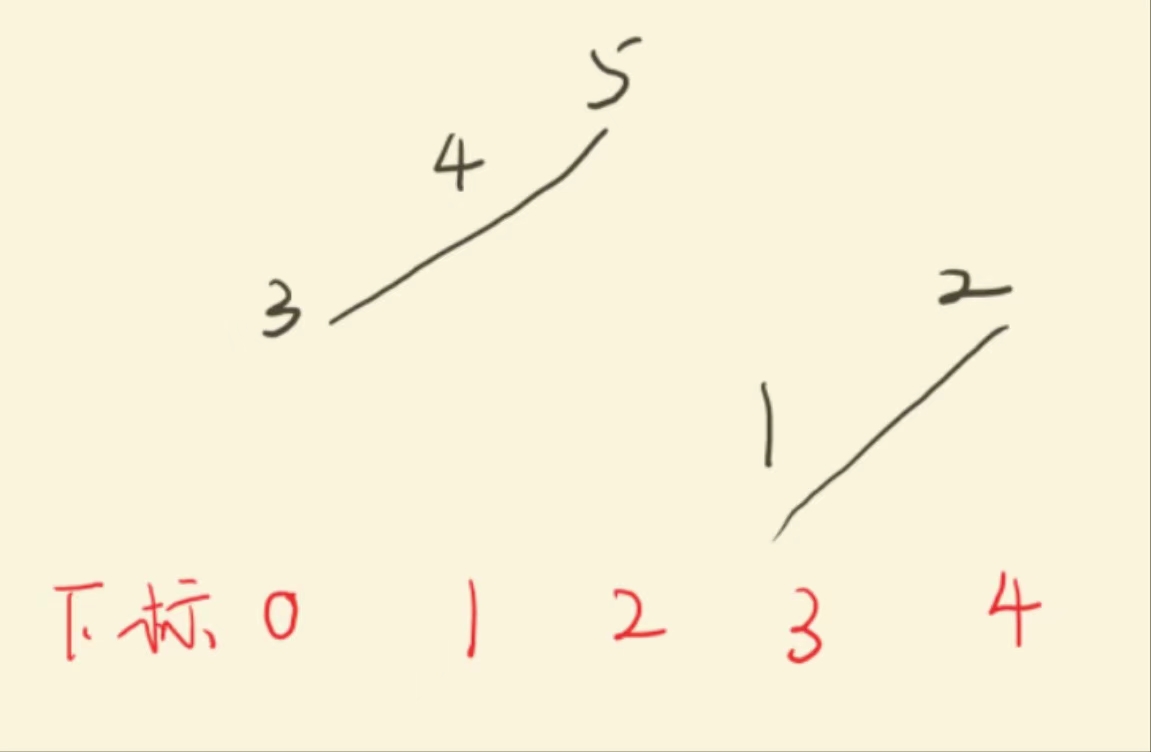
而这就是一个二段性,使得查找区间能够⼀分为二,也是二分查找的本质。
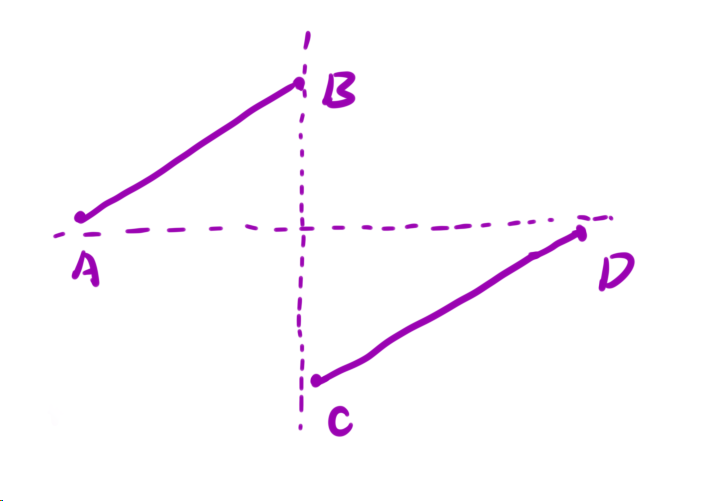
而这个二段性还可以继续抽象成上图,其中 C 点就是我们要求的点。
因此,初始化左右两个指针 left , right :
然后根据 mid 的落点,我们可以这样划分下⼀次查询的区间:
▪ 当 mid 在 [A,B] 区间的时候,也就是 mid 位置的值严格大于 D 点的值,下⼀次查询区间在 [mid + 1,right] 上;
▪ 当 mid 在 [C,D] 区间的时候,也就是 mid 位置的值严格小于等于 D 点的值,下次查询区间在[left,mid] 上。
当区间长度变成 1 的时候,就是我们要找的结果。
具体实现请看下面代码👇
三、完整代码
class Solution {public int findMin(int[] nums) {int left = 0;int right = nums.length - 1;int x = nums[right];while(left < right){int mid = left + (right - left - 1) / 2;if(x < nums[mid]){left = mid + 1;}else{right = mid;}}return nums[left];}
}以上就是本篇博客的全部内容啦,如有不足之处,还请各位指出,期待能和各位一起进步!
相关文章:

「优选算法刷题」:寻找旋转排序数组中的最小值
一、题目 已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums [0,1,2,4,5,6,7] 在变化后可能得到: 若旋转 4 次,则可以得到 [4,5,6,7,0,1,2]若旋转 7 次…...

MySQL 基础入门指南:从安装到基本操作
一、简介 MySQL 是一种流行的开源关系型数据库管理系统,被广泛用于各种规模和类型的应用程序中。如果您对 MySQL 还不熟悉,本文将为您提供一个基础的入门指南,从安装到基本操作。 1.1 安装 MySQL 首先,您需要下载并安装 MySQL。…...

嵌入式Qt Qt Creator安装与工程介绍
一.Qt概述 什么是Qt:Qt是一个跨平台的C图形用户界面应用程序框架。它为应用程序开发者提供建立图形界面所需的所有功能。它是完全面向对象的,很容易扩展,并且允许真正的组件编程。 二.Qt Creator下载安装 下载地址:Index of /a…...

Windows 系统盘(C盘)爆红如何清理、如何增加C盘空间
1、简介 Windows系统中,系统和保留占用太多的空间,一旦系统盘分配空间较少,使用一段时间后,备份文件、临时文件、系统更新记录等都会在占用系统盘较大空间,导致系统盘空间不够使用,会造成应用运行卡顿。如何…...
【JavaEE Spring】Spring 原理
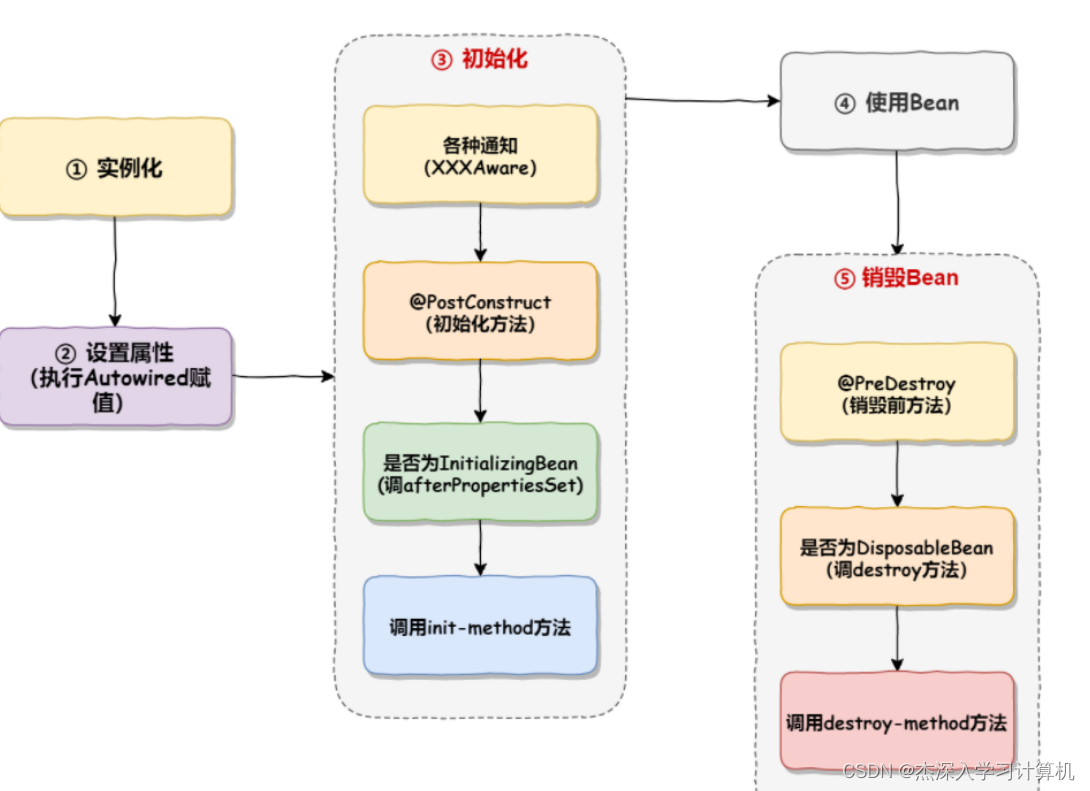
Spring 原理 1. Bean的作⽤域1.1 概念1.2 Bean的作⽤域 2. Bean的⽣命周期 1. Bean的作⽤域 1.1 概念 在Spring IoC&DI阶段, 我们学习了Spring是如何帮助我们管理对象的. 通过 Controller , Service , Repository , Component , Configuration ,Bean 来声明Bean对象。通…...

【Crypto | CTF】RSA打法
天命:我发现题题不一样,已知跟求知的需求都不一样 题目一:已知 p q E ,计算T,最后求D 已知两个质数p q 和 公钥E ,通过p和q计算出欧拉函数T,最后求私钥D 【密码学 | CTF】BUUCTF RSA-CSDN…...

红衣大叔讲AI:从OpenAI发布首个视频大模型Sora,谈2024年视觉大模型的十大趋势
OpenAI宣布推出全新的生成式人工智能模型“Sora”。据了解,通过文本指令,Sora可以直接输出长达60秒的视频,并且包含高度细致的背景、复杂的多角度镜头,以及富有情感的多个角色。 OpenAI发布首个视频大模型Sora,一句话生…...

java远程连接Linux执行命令的三种方式
java远程连接Linux执行命令的三种方式 1. 使用JDK自带的RunTime类和Process类实现2. ganymed-ssh2 实现3. jsch实现4. 完整代码:执行shell命令下载和上传文件 1. 使用JDK自带的RunTime类和Process类实现 public static void main(String[] args){Process proc Run…...

JavaScript- let var const区别
let 允许你声明⼀个作⽤域被限制在块级中的变量、语句或者表达式 let 绑定不受变量提升的约束,这意味着 let 声明不会被提升到当前 该变量处于从块开始到初始化处理的“暂存死区” function example() {let x 10;if (true) {let x 20;console.log(x); // Outpu…...

指针的经典笔试题
经典的指针试题,让你彻底理解指针 前言 之前对于指针做了一个详解,现在来看一些关于指针的经典面试题。 再次说一下数组名 数组名通常表示的都是首元素的地址,但是有两个意外,1.sizeof(数组名)这里数组名…...

书生浦语大模型实战营-课程笔记(1)
模型应用过程,大致还是了解的。和之前实习做CV项目的时候比起来,多了智能体这个环节。智能体是个啥? 类似上张图,智能体不太清楚。感觉是偏应用而不是模型的东西? 数据集类型很多,有文本/图片/视频。所以…...
磁盘database数据恢复: ddrescue,dd和Android 设备的数据拷贝
ddrescue和dd 区别: GNU ddrescue 不是 dd 的衍生物,也与 dd 没有任何关系 除了两者都可用于将数据从一台设备复制到另一台设备。 关键的区别在于 ddrescue 使用复杂的算法来复制 来自故障驱动器的数据,尽可能少地造成额外的损坏。ddrescue…...
SpringMVC-入门
1.概念 SpringMVC是一种软件架构思想,把软件按照模型(Model)、视图(View)、控制器(Controller)这三层来划分。Model:指的是工程中JavaBean,用来处理数据View:指的是工程中的html、jsp等页面,用来展示给用户数据Control…...

需要学习的知识点清单
div 4 div 3 F :拓扑排序 G : 组合数学 D : 结构体排序 div 2 div 12...
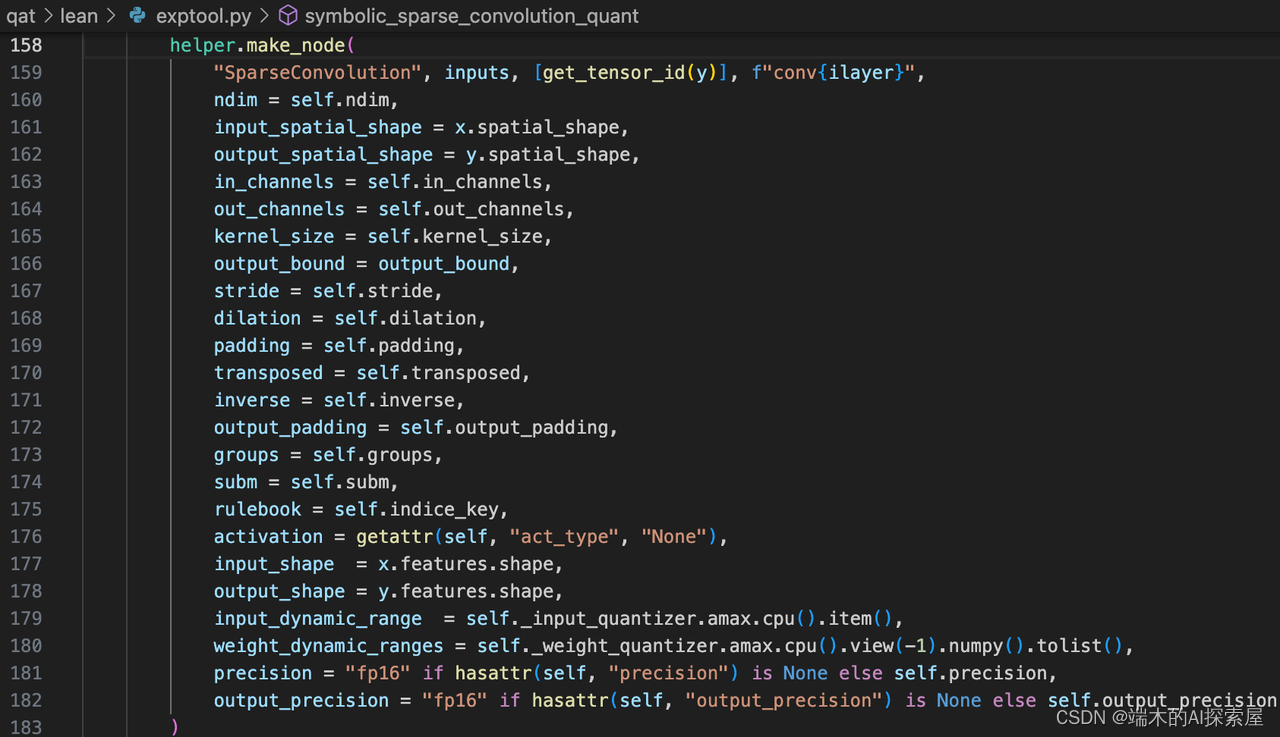
杂谈--spconv导出中onnx的扩展阅读
Onnx 使用 Onnx 介绍 Onnx (Open Neural Network Exchange) 的本质是一种 Protobuf 格式文件,通常看到的 .onnx 文件其实就是通过 Protobuf 序列化储存的文件。onnx-ml.proto 通过 protoc (Protobuf 提供的编译程序) 编译得到 onnx-ml.pb.h 和 onnx-ml.pb.cc 或 on…...
-Linux ARM驱动编程第二天-arm ads下的start.S分析(物联技术666))
嵌入式培训机构四个月实训课程笔记(完整版)-Linux ARM驱动编程第二天-arm ads下的start.S分析(物联技术666)
链接:https://pan.baidu.com/s/1E4x2TX_9SYhxM9sWfnehMg?pwd1688 提取码:1688 ; ; NAME: 2440INIT.S ; DESC: C start up codes ; Configure memory, ISR ,stacks ; Initialize C-variables ; 完全注释 ; HISTORY: ; 2002.02.25:kwtark: ver 0.…...
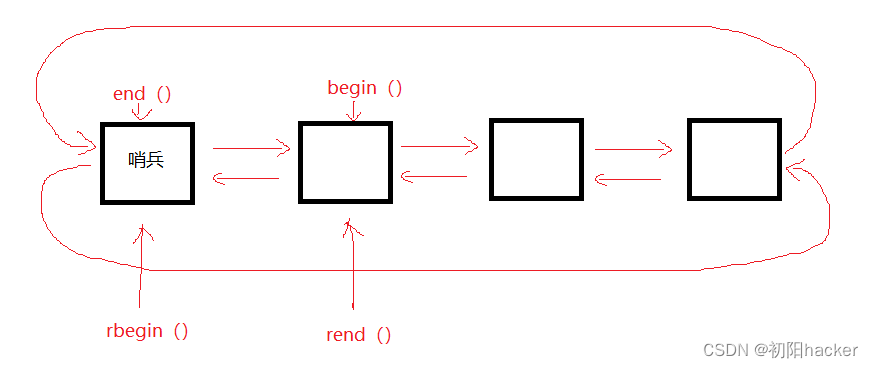
STL之list容器的介绍与模拟实现+适配器
STL之list容器的介绍与模拟实现适配器 1. list的介绍2. list容器的使用2.1 list的定义2.2 list iterator的使用2.3 list capacity2.4 list element access2.5 list modifiers2.6 list的迭代器失效 3. list的模拟实现3.1 架构搭建3.2 迭代器3.2.1 正向迭代器3.2.2反向迭代器适配…...

Leetcode With Golang 二叉树 part1
这一部分主要来梳理二叉树题目最简单最基础的部分,包括遍历,一些简单题目。 一、Leecode 144 - 二叉树的前序遍历 https://leetcode.cn/problems/binary-tree-preorder-traversal/description/ 二叉树的遍历是入门。我们需要在程序一开始就创建一个空…...
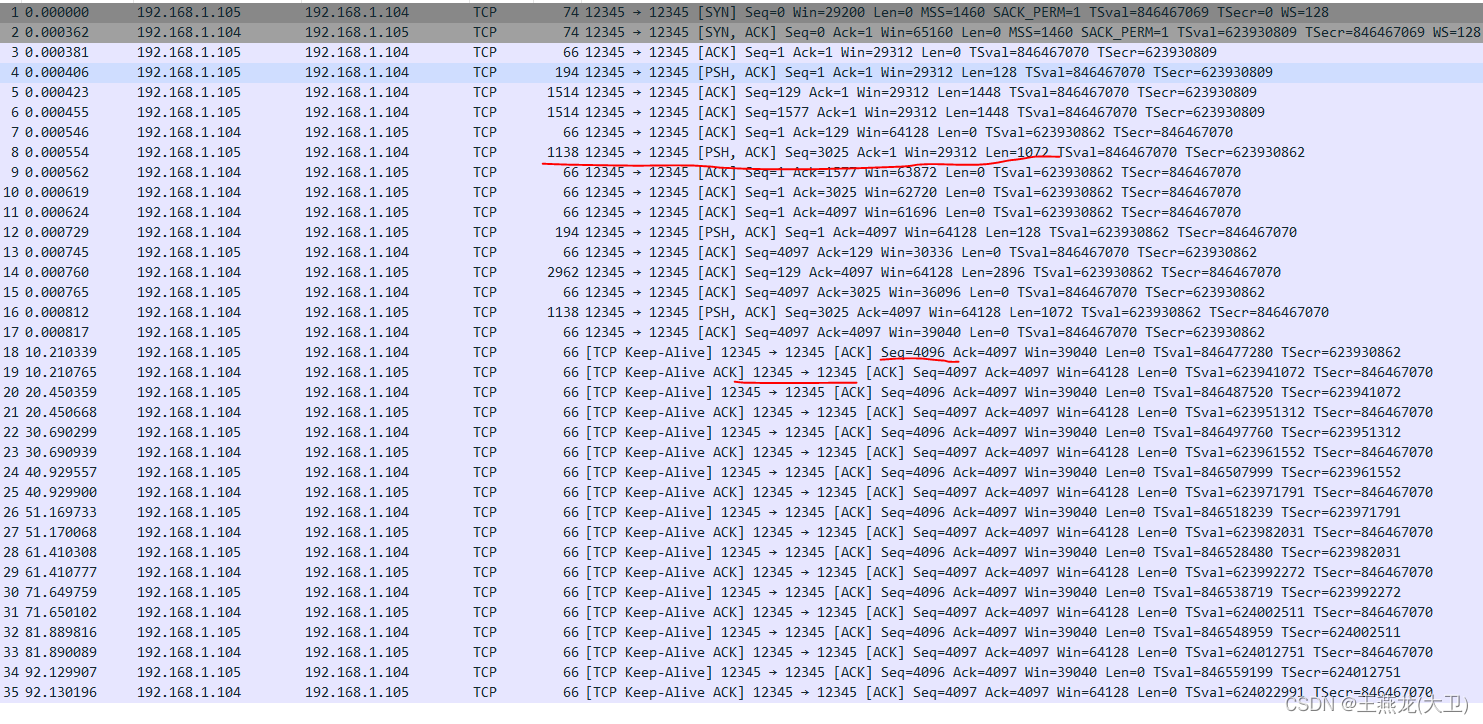
tcp 中使用的定时器
定时器的使用场景主要有两种。 (1)周期性任务 这是定时器最常用的一种场景,比如 tcp 中的 keepalive 定时器,起到 tcp 连接的两端保活的作用,周期性发送数据包,如果对端回复报文,说明对端还活着…...

黑马Java——IO流
一、IO流的概述 IO流:存储和读取数据的解决方案 IO流和File是息息相关的 1、IO流的分类 1.1、纯文本文件 word、Excel不是纯文本文件 而txt或者md文件是纯文本文件 2、小结 二、IO流的体系结构 三、字节流 1、FileOutputStream(字节输出流ÿ…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...
