Leetcode 516.最长回文子序列
题意理解:
给你一个字符串
s,找出其中最长的回文子序列,并返回该序列的长度。子序列定义为:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。
回文理解为元素对称的字串,这里求字符串中最长的对称字串的长度。
使用动态规划的思路来进行解题。
解题思路:
(1)定义dp数组
dp[i][j]表示从i到j的字串中最长回文序列的长度
(2)递推公式
当且仅当s[i]==s[j]
dp[i][j]=dp[i+1][j-1]+2
否则:dp[i][j]=Max(dp[i+1][j],dp[i][j-1],dp[i+1][j-1])
(3) 初始化:一个元素是回文,所以dp[i][j],i==j时,值为1
(4)由于dp[i][j]受dp[i+1][j-1]影响,所以,遍历顺序从左到右,从上到下
最后返回dp[0][s.size-1]
1.动态规划解题
public int longestPalindromeSubseq(String s) {int[][] dp=new int[s.length()][s.length()];for(int i=0;i<s.length();i++){Arrays.fill(dp[i],0);dp[i][i]=1;}for(int i=s.length()-1;i>=0;i--){for(int j=i+1;j<s.length();j++){if(s.charAt(i)==s.charAt(j)){dp[i][j]=dp[i+1][j-1]+2;}else{dp[i][j]=Math.max(Math.max(dp[i][j-1],dp[i+1][j]),dp[i+1][j-1]);}}}return dp[0][s.length()-1];}2.复杂度分析
时间复杂度:O(n^2)
空间复杂度:O(n^2)
相关文章:

Leetcode 516.最长回文子序列
题意理解: 给你一个字符串 s ,找出其中最长的回文子序列,并返回该序列的长度。 子序列定义为:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。 回文理解为元素对称的字串,这里…...
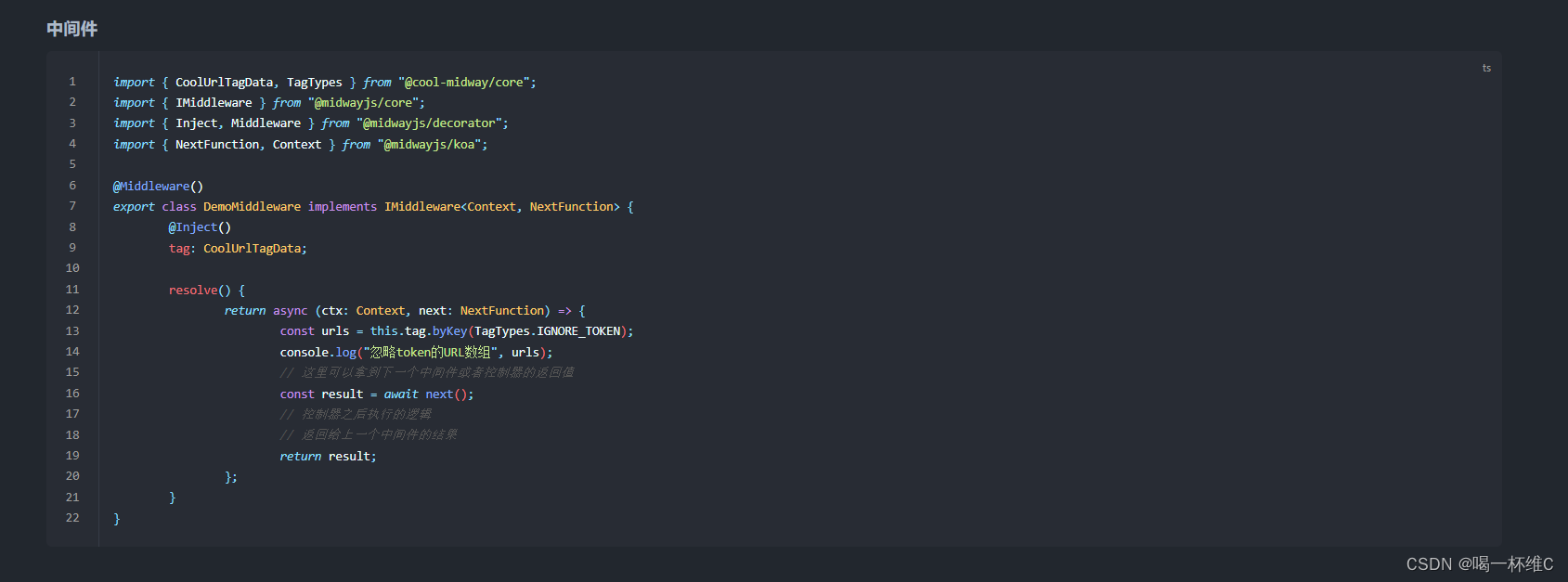
cool Node后端 中实现中间件的书写
1.需求 在node后端中,想实现一个专门鉴权的文件配置,可以这样来解释 就是 有些接口需要token调用接口,有些接口不需要使用token 调用 这期来详细说明一下 什么是中间件中间件顾名思义是指在请求和响应中间,进行请求数据的拦截处理…...
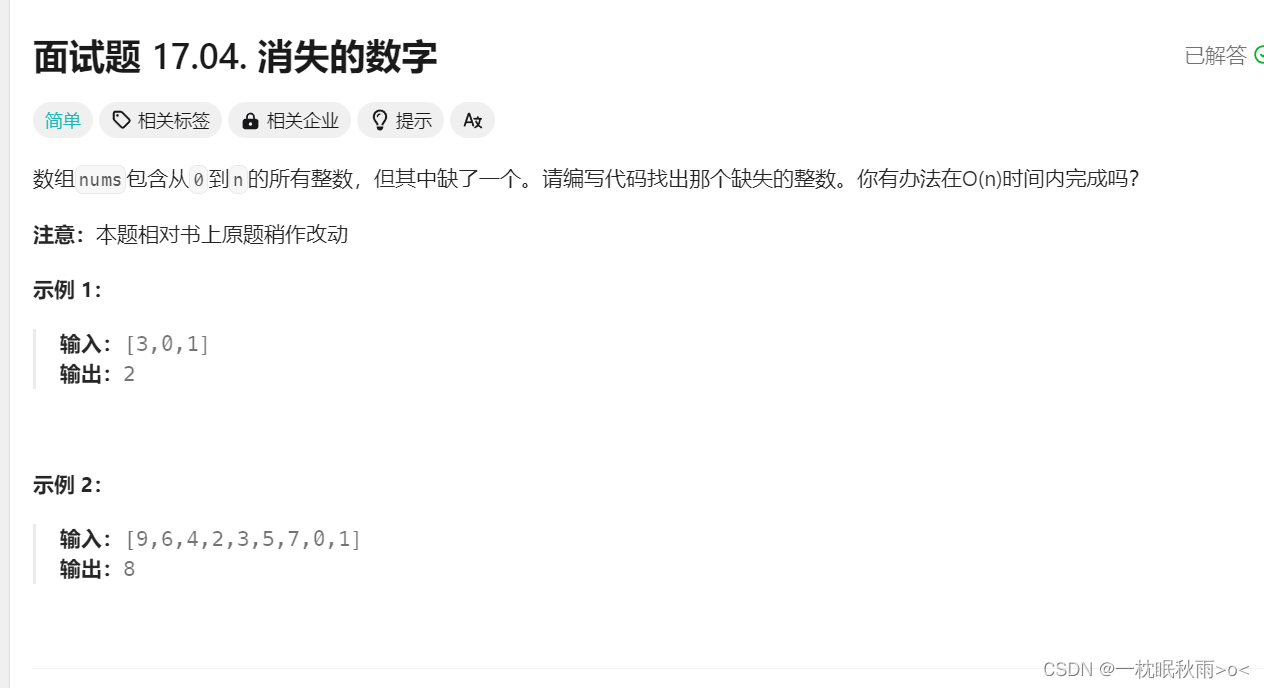
Leecode之面试题消失的数字
一.题目及剖析 https://leetcode.cn/problems/missing-number-lcci/description/ 数组nums包含从0到n的所有整数,但其中缺了一个。请编写代码找出那个缺失的整数。你有办法在O(n)时间内完成吗? 注意:本题相对书上原题稍作改动 示例 1&…...

STM32的三种下载方式
结果jlink,串口,stlink方式都没有问题,是当时缩减代码,看真正起作用的代码段有哪些,就把GPIO初始化中 /*开启GPIO外部时钟*/RCC_APB2PeriphClockCmd( RCC_APB2Periph_GPIOA, ENABLE); 把开启外部时钟的代码注释掉了。…...
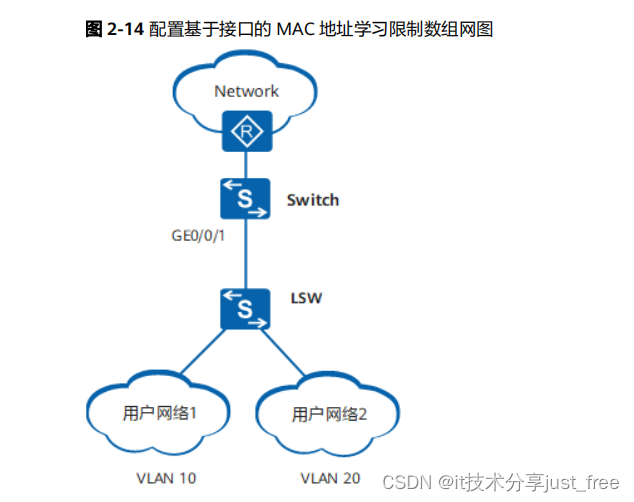
华为 huawei 交换机 接口 MAC 地址学习限制接入用户数量 配置示例
目录 组网需求: 配置思路: 操作步骤: 配置文件: 组网需求: 如 图 2-14 所示,用户网络 1 和用户网络 2 通过 LSW 与 Switch 相连, Switch 连接 LSW 的接口为GE0/0/1 。用户网络 1 和用户网络 2 分别属于 VLAN10 和 V…...

使用Python生成二维码的完整指南
无边落木萧萧下,不如跟着可莉一起游~ 可莉将这篇博客收录在了:《Python》 可莉推荐的优质博主首页:Kevin ’ s blog 本文将介绍如何使用Python中的qrcode库来生成二维码。通过简单的代码示例和详细解释,读者将学习如何在Python中轻…...
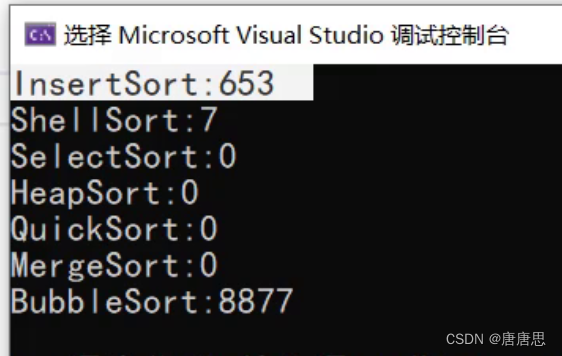
排序前言冒泡排序
目录 排序应用 常见的排序算法 BubbleSort冒泡排序 整体思路 图解分析 代码实现 每趟 写法1 写法2 代码NO1 代码NO2优化 时间复杂度 排序概念 排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递…...

红队笔记Day3-->隧道上线不出网机器
昨天讲了通过代理的形式(端口转发)实现了上线不出网的机器,那么今天就来讲一下如何通过隧道上线不出网机器 目录 1.网络拓扑 2.开始做隧道?No!!! 3.icmp隧道 4.HTTP隧道 5.SSH隧道 1.什么…...

C 练习实例70-求字符串长度
题目:写一个函数,求一个字符串的长度,在 main 函数中输入字符串,并输出其长度。 解答: #include <stdio.h> int length(char *s); int main() {int len;char str[20];printf("请输入字符串:\n");scan…...

HarmonyOS—@State装饰器:组件内状态
State装饰的变量,或称为状态变量,一旦变量拥有了状态属性,就和自定义组件的渲染绑定起来。当状态改变时,UI会发生对应的渲染改变。 在状态变量相关装饰器中,State是最基础的,使变量拥有状态属性的装饰器&a…...
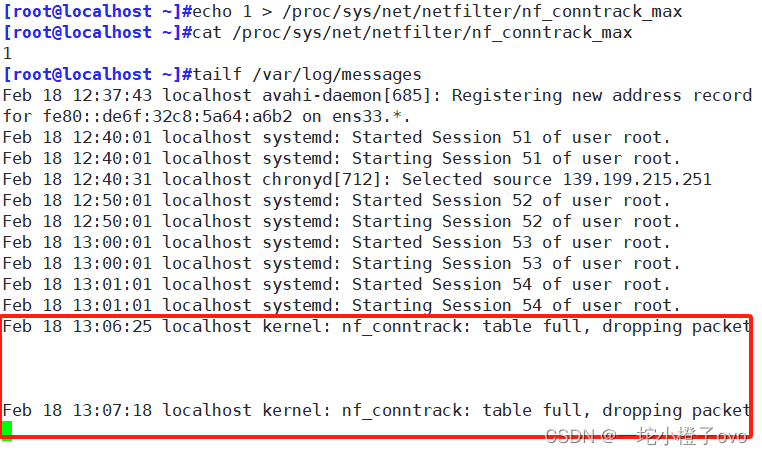
Linux系统——防火墙拓展及重点理解
目录 一、iptables 1.基本语法 2.四表五链——重点记忆 2.1四表 2.2五链 2.3总结 3.iptables选项示例 3.1 -Z 清空流量计数 3.2 -P 修改默认规则 3.3 -D 删除规则 3.4 -R 指定编号替换规则 5.白名单 6.通用匹配 7.示例 7.1添加回环网卡 7.2可以访问端口 7.3 主…...

阿里云短信验证码的两个坑
其它都参照官网即可,其中有两个坑需要注意: 1、除去官网pom引用的包之外,还需要引用以下包: <dependency><groupId>org.apache.httpcomponents.client5</groupId><artifactId>httpclient5</artifact…...
)
c入门第十五篇——学而时习之(阶段性总结)
古人说:“学而时习之。”古人又说:“温故而知新。”古人还说:“读书百遍,其义自见。” 总结一个道理那就是好书要反反复复的读,学习过的知识要时常去复习它,才有可能常读常新。 我:“师弟&…...

抽象的前端
问题背景:vue3,axios 直接导致问题:路由渲染失败 问题报错:Uncaught SyntaxError: The requested module /node_modules/.vite/deps/axios.js?v7bee3286 does not provide an export named post (at LoginIn.vue:16:9) 引入组…...

UPC训练赛二十/20240217
A:无穷力量 题目描述 2022年重庆突发山火让世界看到了中国一个又一个的感人事迹:战士们第一时间奔赴火场,志愿者们自发组成团队,为救火提供一切的可能的服务,人们自发输送物资,有的志愿者甚至几天几夜没有睡觉。每个…...
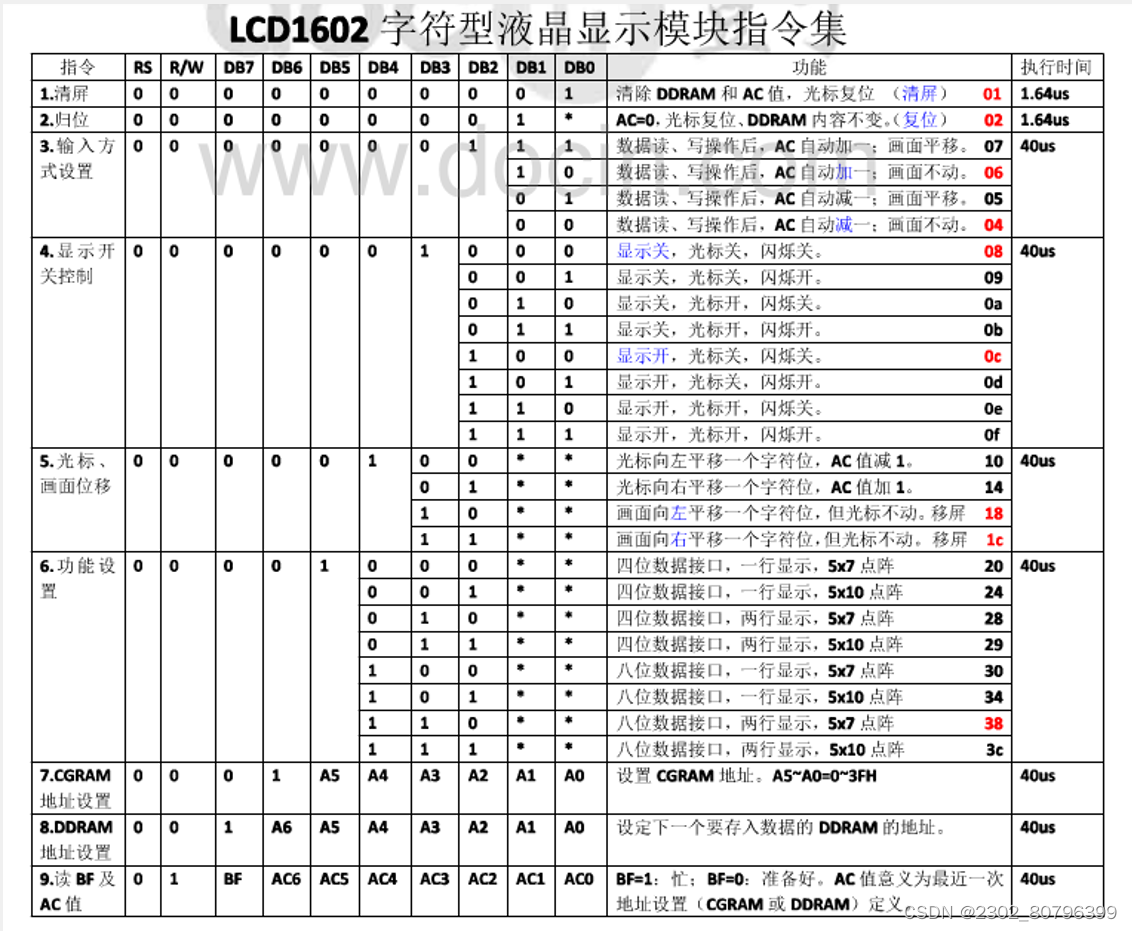
【51单片机】LCD1602(江科大)
1.LCD1602介绍 LCD1602(Liquid Crystal Display)液晶显示屏是一种字符型液晶显示模块,可以显示ASCII码的标准字符和其它的一些内置特殊字符,还可以有8个自定义字符 显示容量:162个字符,每个字符为5*7点阵 2.引脚及应用电路 3.内部结构框图 屏幕: 字模库:类似于数码管的数…...

conda与pip的常用命令
conda的常用命令 1.查看conda版本 $ conda --version conda 23.11.02.查看conda的配置信息 $ conda infoactive environment : baseactive env location : /home/myPc/miniconda3shell level : 1user config file : /home/myPc/.condarcpopulated config files : conda vers…...

你知道什么是物联网MQTT么?
目录 你知道什么是物联网MQTT么?MQTT的基本概念MQTT的工作原理MQTT的应用场景MQTT的实例案例智能家居场景工业监控场景 你知道什么是物联网MQTT么? MQTT(Message Queuing Telemetry Transport)是一种轻量级的、基于发布/订阅模式…...

P8 pair vector
pair是一个模板类,用于表示一对值的组合,用<utility>中 pair模板有两个模板参数,t1 t2,分别表示第一个值和第二个值类型 pair类有两个成员变量,frist和 cond,分别表示第一个值与第二个值 还有一些成员函数和…...

奇异值分解(SVD)的应用——图像压缩
SVD方法是模型降阶的一类重要方法,本征正交分解(POD)和平衡截断(BT)都属于SVD类方法。 要想深入了解模型降阶技术,我们可以先从SVD的应用入手,做一个直观的了解。 1. SVD的定义和分类 我们想寻找…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...
