庖丁解牛-二叉树的遍历
庖丁解牛-二叉树的遍历

〇、前言
01 文章内容
- 一般提到二叉树的遍历,我们是在说
- 前序遍历、中序遍历、后序遍历和层序遍历
- 或者说三序遍历+层序遍历,毕竟三序和层序的遍历逻辑相差比较大
- 下面讨论三序遍历的递归方法、非递归方法和非递归迭代的统一方法
- 然后再讨论一下层序的一般迭代方法(通过队列)
02 力扣网址
- 144. 二叉树的前序遍历 - 力扣(LeetCode)
- 94. 二叉树的中序遍历 - 力扣(LeetCode)
- 145. 二叉树的后序遍历 - 力扣(LeetCode)
一、前序遍历
01 递归实现
- 递归的基本逻辑是比较简单的,但是注意根据题目的需求不同,实现方式是存在差异的
- 如果题目要求主函数返回一个结果列表,那么就要构造一个辅助函数来帮助实现
- 如果题目只要求函数打印前序遍历的序列,那么一个函数就足够了
(1) 返回列表版本1
返回列表版本:辅助函数携带结果列表
public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();inorderTraversalHelper(root,result);return result;}
void preorderTraversalHelper(TreeNode root,List<Integer> result){if(root == null) return;result.add(root.val);inorderTraversalHelper(root.left,result);inorderTraversalHelper(root.right,result);return;
}
(2) 返回列表版本2
返回列表版本:设置全局变量
List<Integer> result = new ArrayList<>();
public List<Integer> preorderTraversal(TreeNode root) {inorderTraversalHelper(root,result);return result;
}
void preorderTraversalHelper(TreeNode root){if(root == null) return;result.add(root.val);inorderTraversalHelper(root.left,result);inorderTraversalHelper(root.right,result);return;
}
(3) 纯真打印版本
public List<Integer> preorderTraversal(TreeNode root) {inorderTraversalHelper(root,result);return result;
}
void preorderTraversal(TreeNode root){if(root == null) return;System.out.print(root.val);inorderTraversalHelper(root.left,result);inorderTraversalHelper(root.right,result);return;
}
(4) 面向对象版本
class Solution {class TraverBox{List<Integer> list;TraverBox(){list = new ArrayList<>();}void preorderTraversalHelper(TreeNode root) {list.add(root.val);}void preTraverHelper(TreeNode root) {if(root == null) return;list.add(root.val);preTraverHelper(root.left);preTraverHelper(root.right);}List<Integer> preTraver(TreeNode root) {preTraverHelper(root);return list;}}public List<Integer> preorderTraversal(TreeNode root) {TraverBox tox = new TraverBox();tox.preTraver(root);return tox.list;}
}
02 非递归实现
(1) 一般迭代法
(2) 统一迭代法
public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result = new LinkedList<>();Stack<TreeNode> stack = new Stack<>();TreeNode subRoot = new TreeNode();if (root != null) stack.push(root); //将根结点入栈while(!stack.isEmpty()){subRoot = stack.pop(); //弹出获取栈顶结点if(subRoot != null){//===右===if(subRoot.right != null){// 添加右结点(空结点不入栈)stack.push(subRoot.right);}//===左===if(subRoot.left != null){// 添加左节点(空结点不入栈)stack.push(subRoot.left);}//===中===stack.push(subRoot); // 添加中结点stack.push(null); // 中结点访问过,但是还没有处理,加入空结点做为标记。}else{ // 只有遇到空结点的时候,才将下一个结点放进结果集result.add(stack.pop().val); //重新取出栈中元素,加入到结果集}}return result;
}
二、中序遍历
01 递归实现
(1) 返回列表版本1
返回列表版本:辅助函数携带结果列表
public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();inorderTraversalHelper(root,result);return result;}
void preorderTraversalHelper(TreeNode root,List<Integer> result){if(root == null) return;inorderTraversalHelper(root.left,result);result.add(root.val);inorderTraversalHelper(root.right,result);return;
}
(2) 返回列表版本2
返回列表版本:设置全局变量
List<Integer> result = new ArrayList<>();
public List<Integer> preorderTraversal(TreeNode root) {inorderTraversalHelper(root,result);return result;
}
void preorderTraversalHelper(TreeNode root){if(root == null) return;inorderTraversalHelper(root.left,result);result.add(root.val);inorderTraversalHelper(root.right,result);return;
}
(3) 纯真打印版本
void preorderTraversal(TreeNode root){if(root == null) return;inorderTraversalHelper(root.left,result);System.out.print(root.val);inorderTraversalHelper(root.right,result);return;
}
02 非递归实现
(1) 一般迭代法
void inOrderNonRecur(){Stack<TreeNode> stack = new Stack<>();TreeNode subRoot = root;if (subRoot != null) {while (!stack.isEmpty() || subRoot != null) {if (subRoot != null) {stack.push(subRoot);subRoot = subRoot.left;} else {subRoot = stack.pop();System.out.print("【"+subRoot.val+"】");subRoot = subRoot.right;}}}
}
(2) 统一迭代法
带注释版本
public List<Integer> inorderTraversal(TreeNode root) {List<Integer> result = new LinkedList<>();Stack<TreeNode> stack = new Stack<>();TreeNode subRoot = new TreeNode();if (root != null) stack.push(root);while (!stack.isEmpty()) {subRoot = stack.pop(); // 将该节点弹出,避免重复操作,下面再将右中左节点添加到栈中if (subRoot != null) {//===右===if(subRoot.right != null){// 添加右节点(空节点不入栈)stack.push(subRoot.right);}//===中===stack.push(subRoot); // 添加中节点stack.push(null); // 中节点访问过,但是还没有处理,加入空节点做为标记。//===左===if(subRoot.left != null){// 添加左节点(空节点不入栈)stack.push(subRoot.left);}} else { // 只有遇到空节点的时候,才将下一个节点放进结果集result.add(stack.pop().val); // 加入到结果集}}return result;
}
无注释版本
public List<Integer> inorderTraversal(TreeNode root) {List<Integer> result = new LinkedList<>();Stack<TreeNode> stack = new Stack<>();TreeNode subRoot = new TreeNode();if (root != null) stack.push(root);while (!stack.isEmpty()) {subRoot = stack.pop();if (subRoot != null) {if(subRoot.right != null) stack.push(subRoot.right);stack.push(subRoot);stack.push(null);if(subRoot.left != null) stack.push(subRoot.left);} else {result.add(stack.pop().val);}}return result;
}
三、后序遍历
01 递归实现
(1) 返回列表版本1
返回列表版本:辅助函数携带结果列表
public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();inorderTraversalHelper(root,result);return result;}
void preorderTraversalHelper(TreeNode root,List<Integer> result){if(root == null) return;inorderTraversalHelper(root.left,result);inorderTraversalHelper(root.right,result);result.add(root.val);return;
}
(2) 返回列表版本2
返回列表版本:设置全局变量
List<Integer> result = new ArrayList<>();
public List<Integer> preorderTraversal(TreeNode root) {inorderTraversalHelper(root,result);return result;
}
void preorderTraversalHelper(TreeNode root){if(root == null) return;inorderTraversalHelper(root.left,result);inorderTraversalHelper(root.right,result);result.add(root.val);return;
}
(3) 纯真打印版本
void preorderTraversal(TreeNode root){if(root == null) return;inorderTraversalHelper(root.left,result);inorderTraversalHelper(root.right,result);System.out.print(root.val);return;
}
02 非递归实现
(1) 一般迭代法
public List<Integer> postorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();if (root != null) {Stack<TreeNode> stack = new Stack<TreeNode>();stack.push(root);TreeNode subRoot = null;while (!stack.isEmpty()) {subRoot = stack.peek();if (subRoot.left != null && root != subRoot.left && root != subRoot.right) {stack.push(subRoot.left);} else if (subRoot.right != null && root != subRoot.right) {stack.push(subRoot.right);} else {result.add(stack.pop().val);root = subRoot;}}}return result;
}
(2) 双栈迭代法
public List<Integer> postOrderNonRecurByTwoStack(){List<Integer> result = new ArrayList<>();TreeNode subRoot = root;if (subRoot != null) {Stack<TreeNode> s1 = new Stack<TreeNode>();Stack<TreeNode> s2 = new Stack<TreeNode>();s1.push(subRoot);while (!s1.isEmpty()) {subRoot = s1.pop();s2.push(subRoot);if (subRoot.left != null) {s1.push(subRoot.left);}if (subRoot.right != null) {s1.push(subRoot.right);}}while (!s2.isEmpty()) {result.add(s2.pop().val);}}
}
(3) 统一迭代法
public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result = new LinkedList<>();Stack<TreeNode> stack = new Stack<>();TreeNode subRoot = new TreeNode();if (root != null) stack.push(root); //将根结点入栈while(!stack.isEmpty()){subRoot = stack.pop(); //弹出获取栈顶结点if(subRoot != null){//===中===stack.push(subRoot); // 添加中结点stack.push(null); // 中结点访问过,但是还没有处理,加入空结点做为标记。//===右===if(subRoot.right != null){// 添加右结点(空结点不入栈)stack.push(subRoot.right);}//===左===if(subRoot.left != null){// 添加左节点(空结点不入栈)stack.push(subRoot.left);}}else{ // 只有遇到空结点的时候,才将下一个结点放进结果集result.add(stack.pop().val); //重新取出栈中元素,加入到结果集}}return result;
}
四、层序遍历
01 不分层输出
class Solution {public int[] levelOrder(TreeNode root) {//if(root == null) return new int[]{};ArrayList<Integer> result = new ArrayList<Integer>();Queue<TreeNode> queue = new LinkedList<TreeNode>();TreeNode subRoot = new TreeNode();if(root != null) queue.offer(root);while(!queue.isEmpty()){subRoot = queue.poll();result.add(subRoot.val);if(subRoot.left != null) queue.add(subRoot.left);if(subRoot.right != null) queue.add(subRoot.right);}int[] dest = new int[result.size()];for(int i = 0 ; i < result.size() ; i++){dest[i] = result.get(i);}return dest;}
}
02 分层输出
public List<List<Integer>> levelOrder(TreeNode root) {List<List<Integer>> ret = new ArrayList<List<Integer>>();if (root == null) {return ret;}Queue<TreeNode> queue = new LinkedList<TreeNode>();queue.offer(root);while (!queue.isEmpty()) {List<Integer> level = new ArrayList<Integer>();int currentLevelSize = queue.size();for (int i = 1; i <= currentLevelSize; ++i) {TreeNode node = queue.poll();level.add(node.val);if (node.left != null) {queue.offer(node.left);}if (node.right != null) {queue.offer(node.right);}}ret.add(level);}return ret;
}
相关文章:

庖丁解牛-二叉树的遍历
庖丁解牛-二叉树的遍历 〇、前言 01 文章内容 一般提到二叉树的遍历,我们是在说 前序遍历、中序遍历、后序遍历和层序遍历 或者说三序遍历层序遍历,毕竟三序和层序的遍历逻辑相差比较大下面讨论三序遍历的递归方法、非递归方法和非递归迭代的统一方法然…...
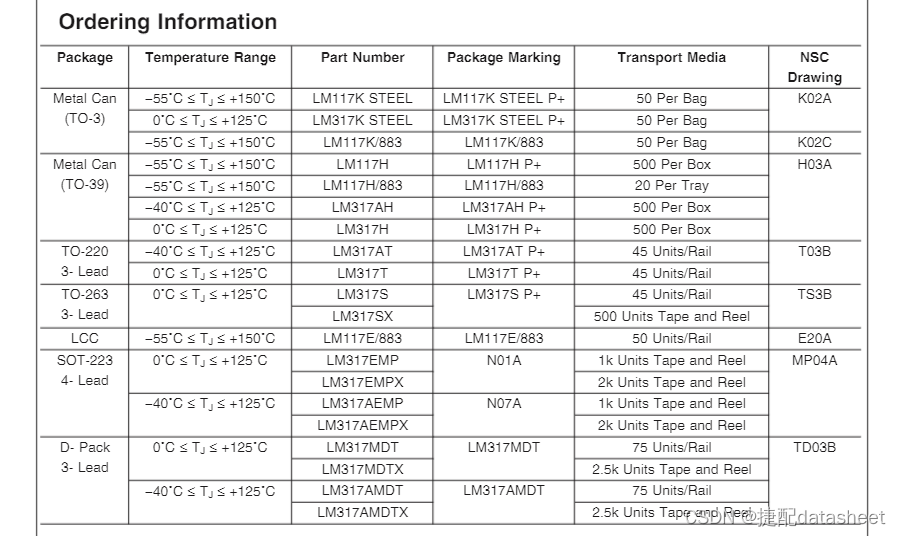
一文了解LM317T的引脚介绍、参数解读
LM317T是一种线性稳压器件,它具有稳定输出电压的特性。LM317T可以通过调整其输出电阻来确保输出电压的稳定性,因此被广泛应用于各种电子设备中。 LM317T引脚图介绍 LM317T共有3个引脚,分别是: 输入引脚(输入电压V_in&…...
【2024.02.22】定时执行专家 V7.0 发布 - TimingExecutor V7.0 Release - 龙年春节重大更新版本
目录 ▉ 新版本 V7.0 下载地址 ▉ V7.0 新功能 ▼2024-02-21 V7.0 - 更新日志▼ ▉ V7.0 新UI设计 ▉ 新版本 V7.0 下载地址 BoomWorks软件的最新版本-CSDN博客文章浏览阅读10w次,点赞9次,收藏41次。▉定时执行专家—毫秒精度、专业级的定时任务执行…...
☀️将大华摄像头画面接入Unity 【1】配置硬件和初始化摄像头
一、硬件准备 目前的设想是后期采用网口供电的形式把画面传出来,所以这边我除了大华摄像头还准备了POE供电交换机,为了方便索性都用大华的了,然后全都连接电脑主机即可。 二、软件准备 这边初始化摄像头需要用到大华的Configtool软件&#…...

直流电流电压变送器4-20mA 10V信号隔离转换模拟量精度变送器
品牌:泰华仪表 型号:TB-IP(U)XX 产地:中国大陆 省份:安徽省 地市:宿州市 颜色分类:4-20mA转4-20mA,4-20mA转0-10V,4-20mA转0-20mA,4-20mA转0-5V,0-20mA转0-20mA,0-20mA转4-20mA,0-20mA转0-10V,0-20mA转…...
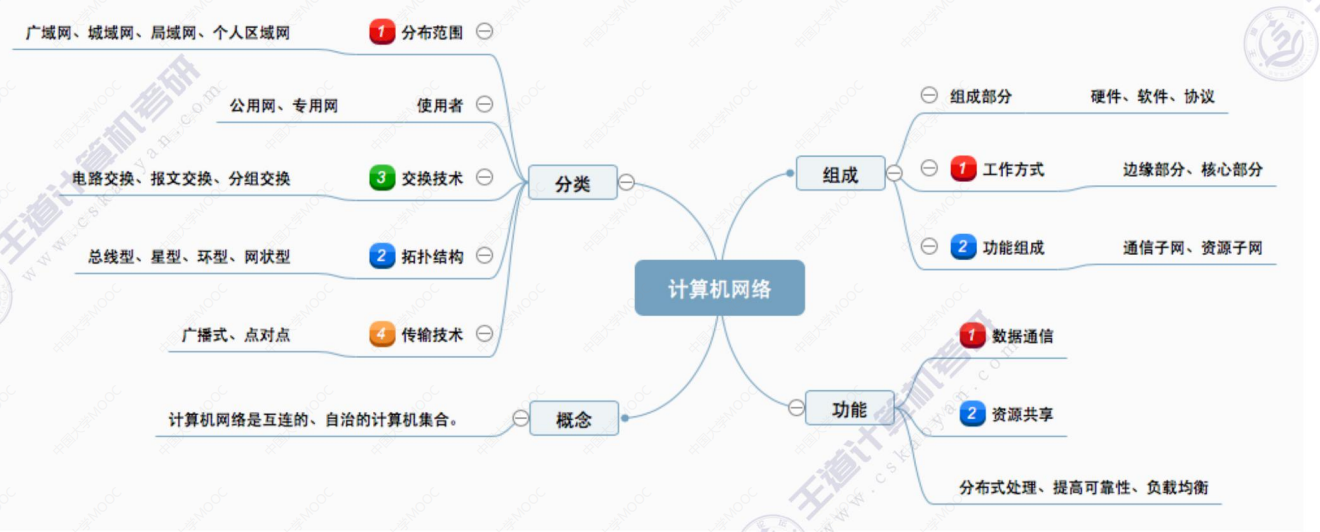
1.1 计算机网络的概念、功能、组成和分类
文章目录 1.1 计算机网络的概念、功能、组成和分类(一)计算机网络的概念(二)计算机网络的功能(三)计算机网络的组成1.组成部分2.工作方式3.功能组成 (四)计算机网络的分类 总结 1.1 …...
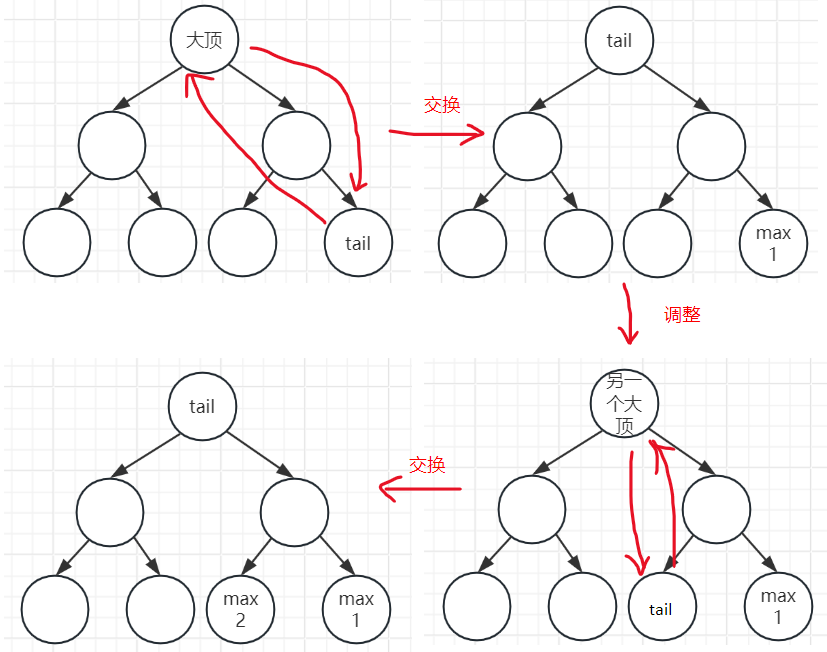
排序算法整理
排序种类排序特性代码背景 基于插入的排序直接插入排序原理代码 折半查找排序2路查找排序希尔排序(shell) 缩小增量排序原理代码 基于交换的排序冒泡排序原理代码 快速排序(重要!)原理我的思考 代码 基于选择的排序(简单)选择排序…...

ONLYOFFICE 桌面应用程序 v8.0 发布:全新 RTL 界面、本地主题、Moodle 集成等你期待的功能来了!
目录 📘 前言 📟 一、什么是 ONLYOFFICE 桌面编辑器? 📟 二、ONLYOFFICE 8.0版本新增了那些特别的实用模块? 2.1. 可填写的 PDF 表单 2.2. 双向文本 2.3. 电子表格中的新增功能 单变量求解:…...
c语言---数组(超级详细)
数组 一.数组的概念二. 一维数组的创建和初始化2.1数组的创建2.2数组的初始化错误的初始化 2.3 数组的类型 三. 一维数组的使用3.1数组的下标3.2数组元素的打印3.2数组元素的输入 四. 一维数组在内存中的存储五. 二维数组的创建5.1二维数组的概念5.2如何创建二维数组 六.二维数…...

神经网络权重初始化
诸神缄默不语-个人CSDN博文目录 (如果只想看代码,请直接跳到“方法”一节,开头我介绍我的常用方法,后面介绍具体的各种方案) 神经网络通过多层神经元相互连接构成,而这些连接的强度就是通过权重ÿ…...

代码随想录训练营第三十九天|62.不同路径63. 不同路径 II
62.不同路径 1确定dp数组(dp table)以及下标的含义 从(0,0)出发到(i,j)有 dp[i][j]种路径 2确定递推公式 dp[i][j]dp[i-1][j]dp[i][j-1] 3dp数组如何初始化 for(int i0;i<m…...
学习大数据所需的java基础(5)
文章目录 集合框架Collection接口迭代器迭代器基本使用迭代器底层原理并发修改异常 数据结构栈队列数组链表 List接口底层源码分析 LinkList集合LinkedList底层成员解释说明LinkedList中get方法的源码分析LinkedList中add方法的源码分析 增强for增强for的介绍以及基本使用发2.使…...
Python 光速入门课程
首先说一下,为啥小编在即PHP和Golang之后,为啥又要整Python,那是因为小编最近又拿起了 " 阿里天池 " 的东西,所以小编又不得不捡起来大概五年前学习的Python,本篇文章主要讲的是最基础版本,所以比…...

解决vite打包出现 “default“ is not exported by “node_modules/...问题
项目场景: vue3tsvite项目打包 问题描述 // codemirror 编辑器的相关资源 import Codemirror from codemirror;error during build: RollupError: "default" is not exported by "node_modules/vue/dist/vue.runtime.esm-bundler.js", impor…...

c语言strtok的使用
strtok函数的作用为以指定字符分割字符串,含有两个参数,第一个函数为待分割的字符串或者空指针NULL,第二个参数为分割字符集。 对一个字符串首次使用strtok时第一个参数应该是待分割字符串,strtok以指定字符完成第一次分割后&…...
hash,以及数据结构——map容器
1.hash是什么? 定义:hash,一般翻译做散列、杂凑,或音译为哈希,是把任意长度的输入(又叫做预映射pre-image)通过散列算法变换成固定长度的输出, 该输出就是散列值。这种转换是一种压缩映射&…...

AIoT网关 人工智能物联网网关
AIoT(人工智能物联网)作为新一代技术的代表,正以前所未有的速度改变着我们的生活方式。在这个智能时代,AIoT网关的重要性日益凸显。它不仅是连接智能设备和应用的关键,同时也是实现智能化家居、智慧城市和工业自动化的必备技术。 一…...

基于YOLOv8/YOLOv7/YOLOv6/YOLOv5的鸟类识别系统(Python+PySide6界面+训练代码)
摘要:本文详细阐述了一个利用深度学习进行鸟类识别的系统,该系统集成了最新的YOLOv8算法,并与YOLOv7、YOLOv6、YOLOv5等先前版本进行了性能比较。该系统能够在图像、视频、实时视频流和批量文件中精确地识别和分类鸟类。文中不仅深入讲解了YO…...

核密度分析
一.算法介绍 核密度估计(Kernel Density Estimation)是一种用于估计数据分布的非参数统计方法。它可以用于多种目的和应用,包括: 数据可视化:核密度估计可以用来绘制平滑的密度曲线或热力图,从而直观地表…...

先进语言模型带来的变革与潜力
用户可以通过询问或交互方式与GPT-4这样的先进语言模型互动,开启通往知识宝库的大门,即时访问人类历史积累的知识、经验与智慧。像GPT-4这样的先进语言模型,能够将人类历史上积累的海量知识和经验整合并加以利用。通过深度学习和大规模数据训…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...
