Codeforces Round 928 (Div. 4) (A-E)
比赛地址 :
https://codeforces.com/contest/1926
A
遍历每一个字符串,比较1和0的数量即可,那个大输出那个;
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'
#define lowbit(x) (x&(-x))
#define sz(a) (int)a.size()
#define pb push_back
#define all(a) a.begin(), a.end()
#define int long long
typedef long long LL;
const int mod = 1e9+7;
const int N = 2e5+10;using namespace std;inline void solve(){int n ; cin >> n ;for(int i=1;i<=n;i++){string s ; cin >> s ;int t = 0 ;for(char c : s){if(c=='A') t++;}if(t>=3) cout << "A" << endl;else cout << "B" << endl;}
}signed main()
{IOSint _ = 1;// cin >> _;while(_ --) solve();return 0;
}B .
模拟,先找第一个出现的'1' , 然后求这一列1的个数(也就是正方形的一条边) : n,然后求'1'的总个数: s,判断n*n==s && 右下角那个点也是1,就能够判断是不是正方形,否则就是三角形 ;
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'
#define lowbit(x) (x&(-x))
#define sz(a) (int)a.size()
#define pb push_back
#define all(a) a.begin(), a.end()
#define int long long
typedef long long LL;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;using namespace std;char a[13][13] ;inline void solve() {int n ; cin >> n ;int t = 0 ;bool tag = true;int x = 0 , y = 0 ;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){cin >> a[i][j] ;if(a[i][j]=='1' && tag){x = i ;y = j ;tag = false ;}if(a[i][j] == '1') t++;}}bool st = false ;int b = 0 ;for(int j=y;j<=n;j++){if(a[x][j]=='1') b++;// 长度 }if(x+b-1<=n&&y+b-1<=n&&a[x+b-1][y+b-1]=='1') st = true ;if(t==b*b && st) cout << "SQUARE" << endl;else cout << "TRIANGLE" << endl ;}signed main()
{IOSint _ = 1;cin >> _;while (_--) solve();return 0;
}C
前缀和 + 预处理
可以通过前缀和进行预处理,为O(2e5+n),然后对于每一个数据,都能够通过O(1)进行输出 ;
#include<bits/stdc++.h>
using namespace std;
typedef long long LL ;
const int N = 2e5 + 10 ;
LL a[N] ;int get(int x){int t = 0 ;while(x) t+=x%10,x/=10;return t ;
}void init(){a[1] = 1 ;for(int i=2;i<=2e5;i++){a[i] = a[i-1] + get(i) ;}
}int main() {int tt ; cin >> tt ;init() ;while(tt--){int n ; cin >> n ;cout << a[n] << endl;}return 0 ;
}
数学 推式子
分情况讨论,推出数学式子 , 然后算出答案 ;
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'
#define lowbit(x) (x&(-x))
#define sz(a) (int)a.size()
#define pb push_back
#define all(a) a.begin(), a.end()
typedef long long LL;
const int mod = 1e9+7;
const int N = 2e5+10;using namespace std;LL get0(int n){LL ans = (n+1)*n/2 ;return ans ;
}
LL get1(int n){int x = n / 10 ;int y = n % 10 ;LL t = x * (x-1) / 2 * 10 + 45 * x + get0(y) + (y+1) * x;return t ;
}LL get2(int n){int x = n / 100 ;int y = n % 100 ;LL t = get1(y) + x * (x-1) / 2 * 100 + x * get1(99) + (y+1) * x;return t ;
}
LL get3(int n){int x = n / 1000 ;int y = n % 1000 ;LL t = get2(y) + x * (x-1) / 2 * 1000 + x * get2(999) + (y+1) * x;return t ;
}
LL get4(int n){int x = n / 10000 ;int y = n % 10000 ;LL t = get3(y) + x * (x-1) / 2 * 10000 + x * get3(9999) + (y+1) * x;return t ;
}inline void solve(){int n ; cin >> n ;if(n<10) {cout << (n+1)*n/2 << endl;return ;}if(n>=10 && n<100){int x = n / 10 ;int y = n % 10 ;LL t = x * (x-1) / 2 * 10 + 45 * x + get0(y) + (y+1) * x;cout << t << endl;return ;}if(n>=100 && n<1000){int x = n / 100 ;int y = n % 100 ;LL t = get1(y) + x * (x-1) / 2 * 100 + x * get1(99) + (y+1) * x;cout << t << endl;return ;}if(n>=1000 && n<10000){int x = n / 1000 ;int y = n % 1000 ;LL t = get2(y) + x * (x-1) / 2 * 1000 + x * get2(999) + (y+1) * x;cout << t << endl;return ;}if(n>=10000 && n<100000){int x = n / 10000 ;int y = n % 10000 ;LL t = get3(y) + x * (x-1) / 2 * 10000 + x * get3(9999) + (y+1) * x;cout << t << endl;return ;}if(n>=100000 && n<1000000){int x = n / 100000 ;int y = n % 100000 ;LL t = get4(y) + x * (x-1) / 2 * 100000 + x * get4(99999) + (y+1) * x;cout << t << endl;return ;}
}signed main()
{IOSint _ = 1;cin >> _;while(_ --) solve();return 0;
}D
哈希表 + 位运算
对于每个数来说,能与它一组的有且仅有二进制在低31位上的31位都完全相反这一个数,那么可以得到一个组最多两个数字,对于x,那么能够与它配对的数字也就是 : ((1<<31)-1) ^ x ,其中((1<<31)-1)代表2^31-1,其二进制的低31位全是一;
通过上面就可以一遍遍历,用map记录之前出现过的数,遇到能匹配的,就删掉一个 ;
int yy = (1<<31) - 1 ;
/ 一对中的所有位都不同的条件等价于当我们对 2个数进行异或时,该对产生的数的所有位都设置为 1
inline void solve2(){int n ; cin >> n ;map<int,int> mp ;int ans = 0 ;for(int i=1;i<=n;i++){int x ; cin >> x ;if(!mp[x]) ++ans,++mp[yy^x];else --mp[x] ;}cout << ans << endl ;
}哈希表 + 字符串
如果不精通位运算,就可以直接采取hash表存字符串的方式;
这里采用set + map进行模拟 ;
LL a[N] ;string get(string s){string str = "" ;for(char c : s) str += c == '1' ? '0' : '1' ;return str;
}inline void solve(){int n ; cin >> n ;for(int i=1;i<=n;i++) cin >> a[i] ;set<string> st ;map<string,int> mp ;int x = 0 ;for(int i=1;i<=n;i++){string s = bitset<32>(a[i]).to_string();s = s.substr(1);string str = get(s) ;if(st.count(str)){x++;if(mp[str]>1){mp[str]--;}else{st.erase(str);mp[str]--;}}else{st.insert(s) ;mp[s]++; } }cout << n - x << endl ;
}E
思维题
对于第一轮,就已经把全部的奇数放完了,那么之后的就全部都是偶数 ;
永远不会在非2的幂的棋步上放下棋 ,因为非2的幂的步上,一定包含一个奇数因子,会在第一轮就被放下 ;
加入上一步还剩n个棋子,那么下一步一定会下其中的一半棋子,然后模拟就好了 ;
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'
#define lowbit(x) (x&(-x))
#define sz(a) (int)a.size()
#define pb push_back
#define all(a) a.begin(), a.end()
#define int long long
typedef long long LL;
const int mod = 1e9+7;
const int N = 2e5+10;using namespace std;// 第一轮 把奇数放完了,后面一定全是偶数
// 永远不会在非2的幂的棋步上放下棋 ,因为非2的幂的步上,一定包含一个奇数因子,会在第一轮就被放下 ;void solve() {int n, k;cin >> n >> k;vector<int> v;while (n) {v.push_back((n + 1) / 2); //每次放奇数个 n /= 2;}int tot = 0, pow2 = 1;for (int x : v) {if (tot < k && k <= tot + x) {cout << pow2 * (2 * (k - tot) - 1) << '\n';return;}tot += x;pow2 *= 2;}
}signed main()
{IOSint _ = 1;cin >> _;while(_ --) solve();return 0;
}相关文章:
 (A-E))
Codeforces Round 928 (Div. 4) (A-E)
比赛地址 : https://codeforces.com/contest/1926 A 遍历每一个字符串,比较1和0的数量即可,那个大输出那个; #include<bits/stdc.h> #define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); #define endl \n #define lowbit(x) (x&am…...

git远程操控gitee
配置SSH公钥 首先,在本地计算机上生成SSH公钥。打开终端或命令提示符窗口,并执行以下命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com"按照提示操作,生成SSH密钥对。默认情况下,公钥将保存在~…...
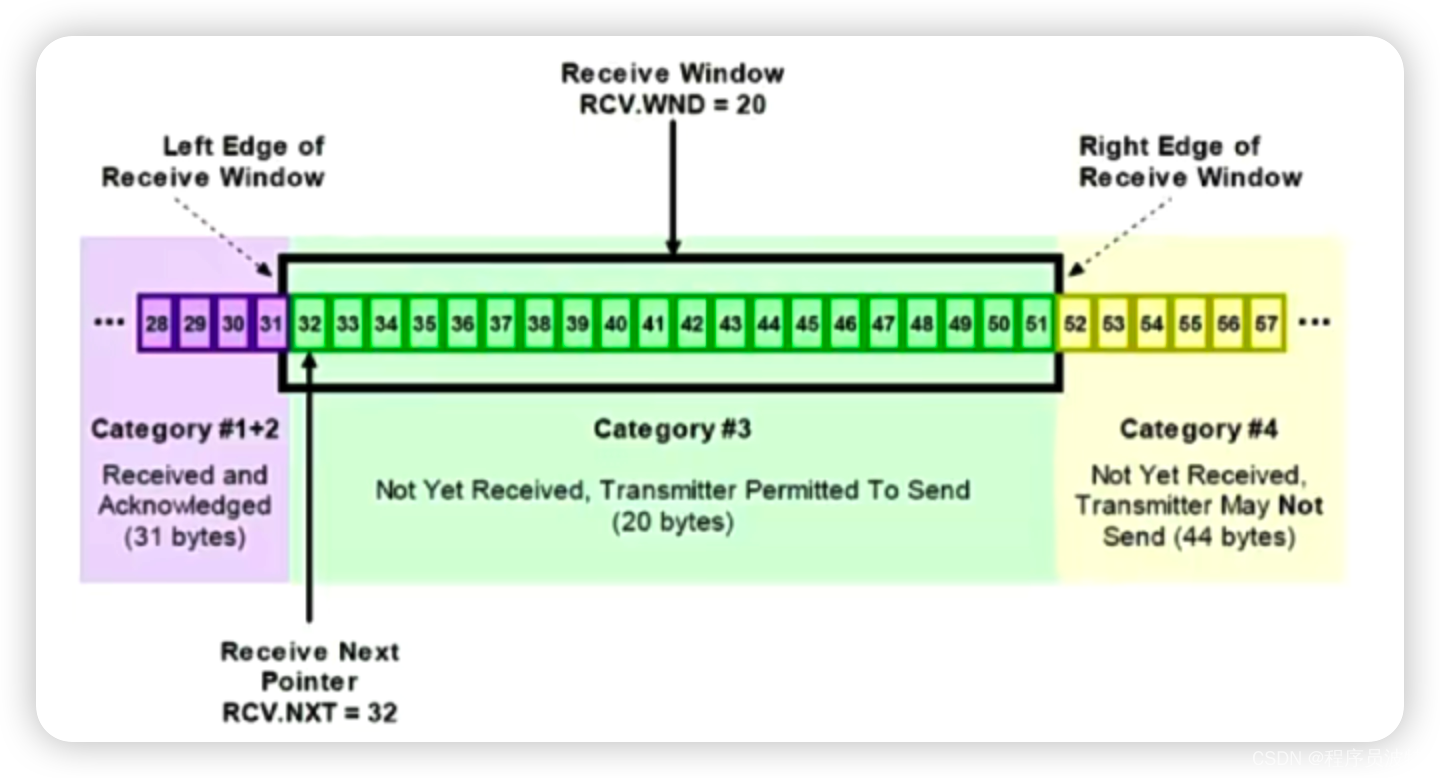
常见面试题:TCP的四次挥手和TCP的滑动窗口
说一说 TCP 的四次挥手。 挥手即终止 TCP 连接,所谓的四次挥手就是指断开一个 TCP 连接时。需要客户端和服务端总共发出四个包,已确认连接的断开在 socket 编程中,这一过程由客户端或服务端任意一方执行 close 来触发。这里我们假设由客户端…...

力扣随笔之两数之和 Ⅱ -输入有序数组(中等167)
思路:在递增数组中找出满足相加之和等于目标数 定义左右两个指针(下标)从数组两边开始遍历,若左右指针所指数字之和大于目标数,则将右指针自减,若左右指针所指数字之和小于目标数,则左指针自加&…...
最优传输(Optimal Transport)
最优传输(Optimal Transport)是一种数学理论和计算方法,用于描述两个概率分布之间的距离或者对应关系。它的核心概念是如何以最佳方式将一组资源(如质量、能量等)从一个位置传输到另一个位置。 基本概念: …...
MIT-6.824-Lab2,Raft部分笔记|Use Go
文章目录 前记Paper6:RaftLEC5、6:RaftLAB22AtaskHintlockingstructureguide设计与编码 2BtaskHint设计与编码 2CtaskHint question后记 LEC5:GO, Threads, and Raftgo threads技巧raft实验易错点debug技巧 前记 趁着研一考完期末有点点空余…...
使用openeuler 22.03替代CentOS 7.9,建立虚拟机详细步骤
进入浏览器搜索网址下载openeuler 22.03镜像文件 https://mirrors.huaweicloud.com/openeuler/openEuler-22.03-LTS-SP3/ISO/x86_64/openEuler-22.03-LTS-SP3-x86_64-dvd.iso 打开VMware Workstation新建一个虚拟机: 自定义虚拟机位置 加入下载好的openeuler镜像文件…...

代理技术引领出海征程
在数字娱乐的繁荣时代,游戏开发者和发行商们意识到,要在全球市场立足,必须迈向国际化的出海之路。然而,这一旅程面临着跨越网络壁垒、适应多元文化和提升全球连接性的巨大挑战。本文将深入探讨代理技术在游戏行业出海过程中的创新…...
谷粒商城篇章9 ---- P248-P261/P292-P294 ---- 消息队列【分布式高级篇六】
目录 1 消息队列(Message Queue)简介 1.1 概述 1.2 消息服务中两个重要概念 1.3 消息队列主要有两种形式的目的地 1.4 JMS和AMQP对比 1.5 应用场景 1.6 Spring支持 1.7 SpringBoot自动配置 1.7 市面上的MQ产品 2 RabbitMQ 2.1 RabbitMQ简介 2.1.1 RabbitMQ简介 2…...
----生命周期事件)
【Spring连载】使用Spring Data访问 MongoDB(五)----生命周期事件
【Spring连载】使用Spring Data访问 MongoDB(五)----生命周期事件Lifecycle Events 一、实体回调Entity Callbacks1.1 实现实体回调1.2 注册实体回调 二、特定存储的实体回调 一、实体回调Entity Callbacks 1.1 实现实体回调 1.2 注册实体回调 二、特…...

JavaSec 之 SQL 注入简单了解
文章目录 JDBC 注入语句拼接(Statement)修复方案 语句拼接(PrepareStatement)修复方案 预编译 JdbcTemplate修复方案 MyBatisLike 注入Order By 注入In 注入 寒假学了一个月 pwn,真心感觉这玩意太底层学的我生理不适应了,接下来学一段时间 java 安全缓一…...

第十一章——期约与异步函数
ECMAScript 6及之后的几个版本逐步加大了对异步编程机制的支持,提供了令人眼前一亮的新特性。ECMAScript 6新增了正式的Promise(期约)引用类型,支持优雅地定义和组织异步逻辑。接下来几个版本增加了使用async和await关键字定义异步…...

工具方法合集-utils.js
通用 import get from lodash.get import cloneDeep from lodash.clonedeep // 深度clone export function deepClone(obj) {return obj ? cloneDeep(obj) : obj } export function lodashGet(obj, key, defaultValue = ) {//这个 defaultValue 不能给默认 值 会报错;retur…...

安卓11-设置HDMI分辨率流程
安卓11中从设置-显示设置hdmi分辨率流程:framework层通过jni控制底层驱动实现,标准驱动模型 packages\apps\Settings\src\com\android\settings\display\HdmiSettings.javaprivate void updateResolution(final ITEM_CONTROL control, final int index) {showWaitin…...
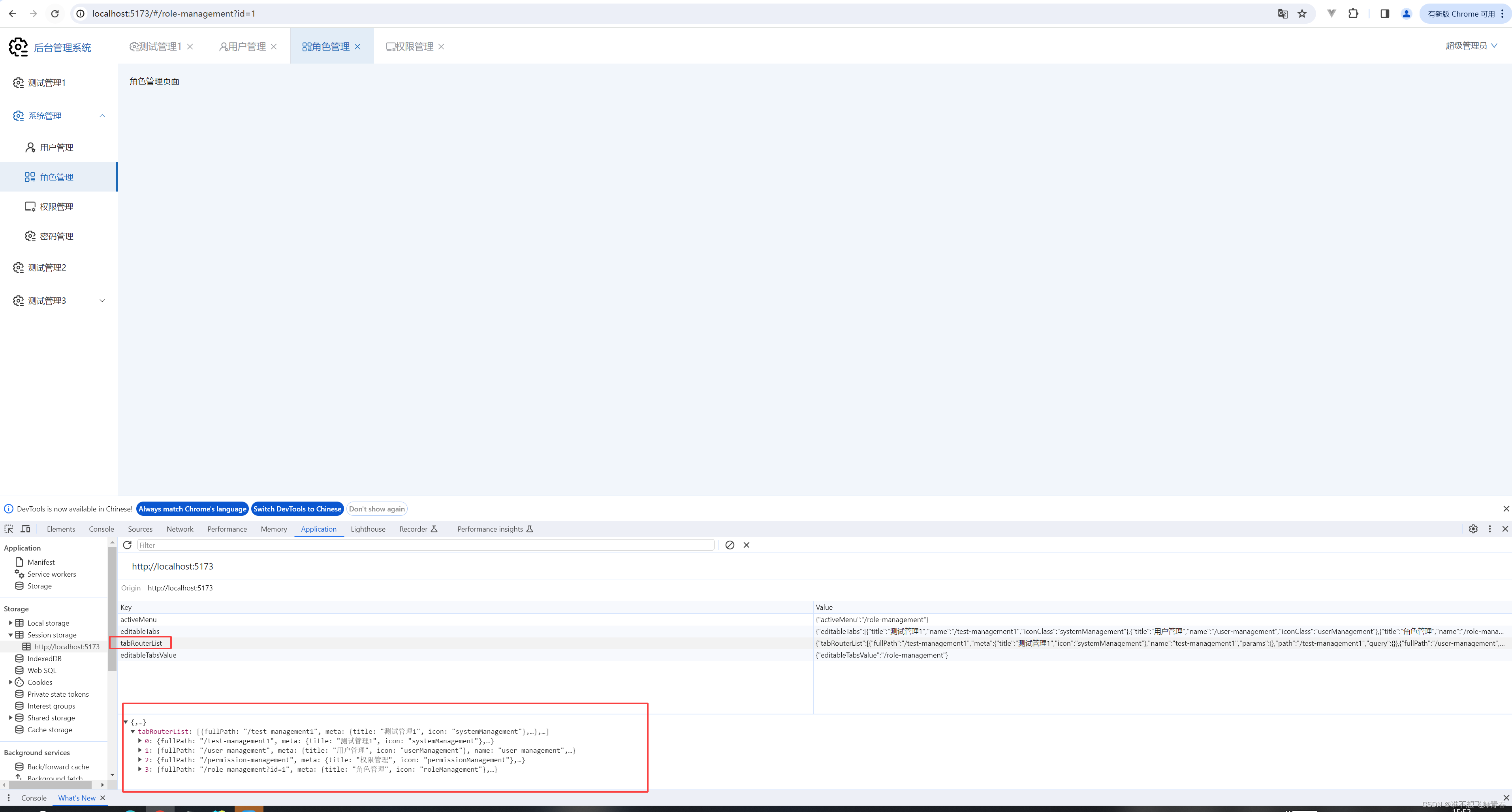
Vue3+vite搭建基础架构(11)--- 菜单栏功能和Tab页功能实现
Vue3vite搭建基础架构(11)--- 菜单栏功能和Tab页功能实现 说明删除项目中不需要的文件userStore全局属性代码菜单栏代码Tab页代码解决浏览器输入地址时不会打开tab页问题和切换tab页时参数丢失问题 说明 这里记录下自己在Vue3vite的项目实现菜单栏功能和…...

餐饮神秘顾客公司:关于餐饮行业神秘顾客调查注意事项
在餐饮业,顾客体验往往决定品牌的成败。为深入了解顾客需求和感受,许多餐饮企业引入“神秘顾客”调查。然而,此调查并非简单走过场,其中细节和注意事项颇多。餐饮行业神秘顾客调查需注意以下几点: 1. 专业培训&#x…...
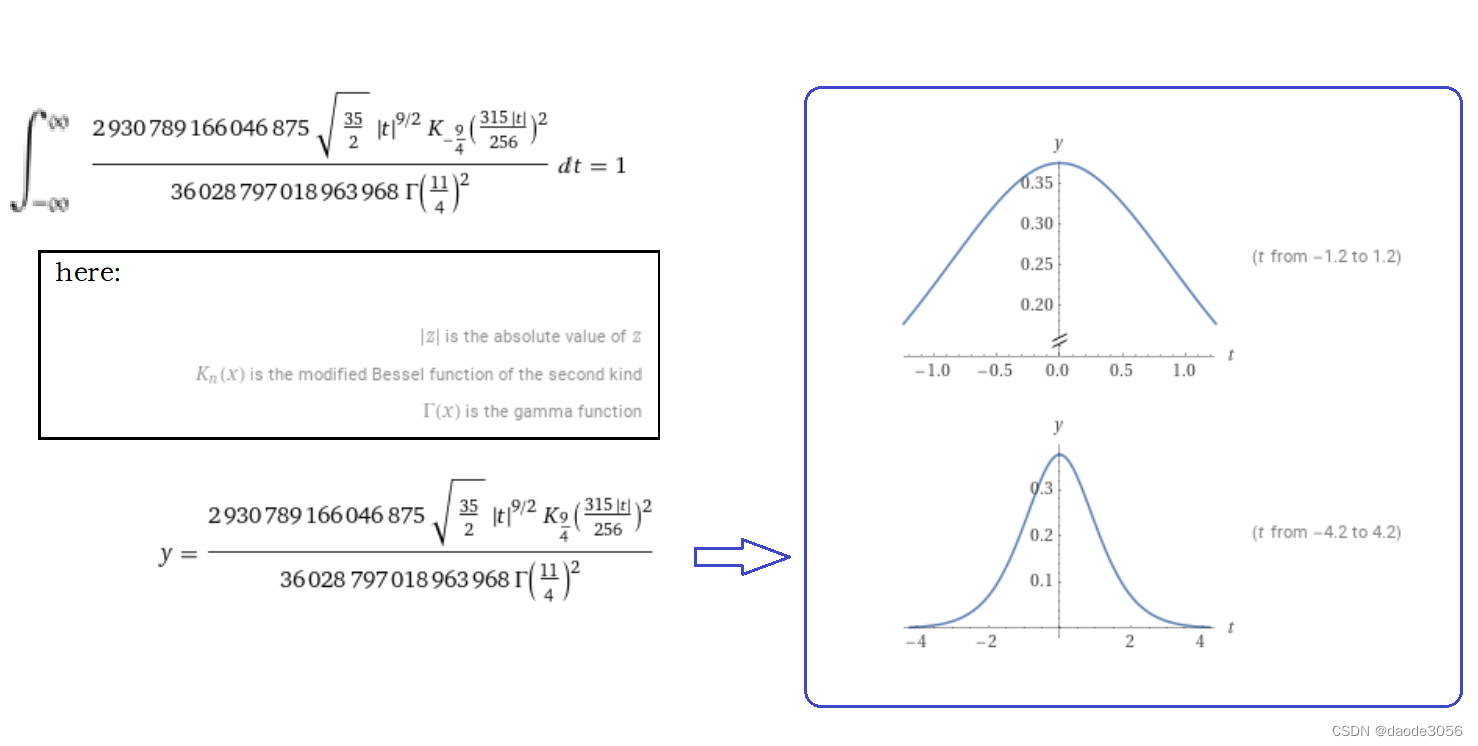
概率密度函数(PDF)与神经网络中的激活函数
原创:项道德(daode3056,daode1212) 在量子力学中,许多现象都是统计的结果,基本上用的是正态分布,然而,从本质上思考,应该还存在低阶的分布,标准的正态分布是它的极限,这样一来,或许在…...
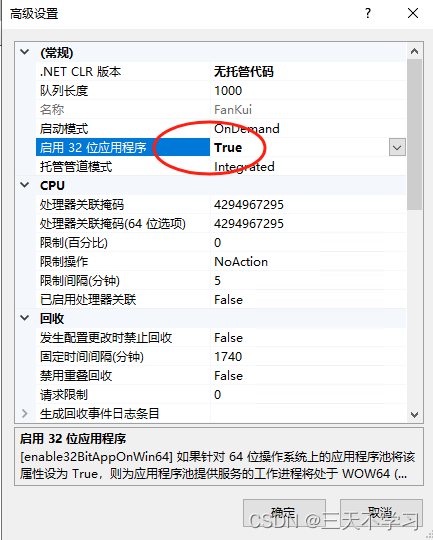
.netcore 6.0/7.0项目迁移至.netcore 8.0 注意事项
1、SqlSugarCore 相关 1.1 主项目添加数据,否则会报数据库连接错误: <InvariantGlobalization>false</InvariantGlobalization> <PropertyGroup><TargetFramework>net8.0</TargetFramework><Nullable>enable</…...
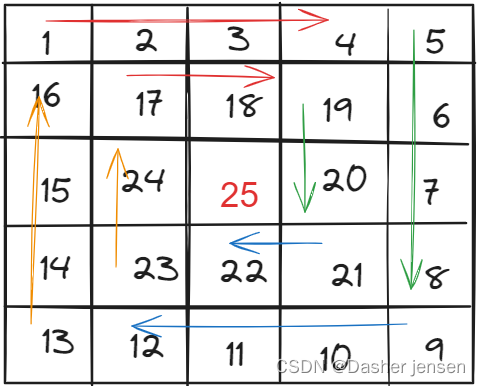
算法打卡day2|数组篇|Leetcode 977.有序数组的平方、 209.长度最小的子数组、59.螺旋矩阵II
算法题 Leetcode 977.有序数组的平方 题目链接: 977.有序数组的平方 大佬视频讲解:977.有序数组的平方 个人思路 第一时间就只想到暴力解法,双重循环一个循环比较一个循环赋值;但这样可能会超时,所以还能用双指针࿰…...

Hive【内部表、外部表、临时表、分区表、分桶表】【总结】
目录 Hive的物种表结构特性 一、内部表 建表 使用场景 二、外部表 建表:关键词【EXTERNAL】 场景: 外部表与内部表可互相转换 三、临时表 建表 临时表横向对比编辑 四、分区表 建表:关键字【PARTITIONED BY】 场景: 五、分桶表 …...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...
