平台组成-监控服务
监控服务和其他服务不同,不是一个单一的微服务,准确来说是一个体系。每个微服务都集成了Actuator,通过Actuator对外提供微服务的运行状况。关于Actuator大家可以阅读这篇文章。《Spring boot——Actuator 详解》
其上是Micrometer,关于Micrometer可以阅读这篇文章《万字长文详解服务性能监控之Micrometer》。
这部分只解决了微服务自身监控。系统还需要监控操作系统运行情况、硬件情况等等,这部分平台是集成了oshi。关于oshi请阅读这篇文章《使用oshi库获取CPU硬件信息》。
平台的理念是开放体系,在各个领域优选成熟方案集成进来。使用平台学习的东西,离开了平台一样用。很多所谓低代码平台的致命缺陷就是封闭,在平台上学习和实践的东西,离开平台将毫无价值,导致开发人员学习意愿非常低。为了解决复杂问题,很多低代码平台要求使用者学习它发明的脚本语言,为什么不直接用JAVA。就像是放着普通话不用,非要去学习某个乡村的地方方言,何苦来着。作为一个资深程序员,我对拖拽生成界面也不认可,我不认为拖拽一个输入控件到界面上,比输入一个<el-input>省了多少事。一个界面大量的工作不是摆个控件,而是数据的提取、数据的校验、数据存入后台这些逻辑工作,是出现问题调试bug这些工作。
千里马平台的核心理念是通过组件的管理的来降低开发工作量和提高稳定性。模块、服务之后将讲解平台的组件体系。
相关文章:

平台组成-监控服务
监控服务和其他服务不同,不是一个单一的微服务,准确来说是一个体系。每个微服务都集成了Actuator,通过Actuator对外提供微服务的运行状况。关于Actuator大家可以阅读这篇文章。《Spring boot——Actuator 详解》 其上是Micrometer&…...
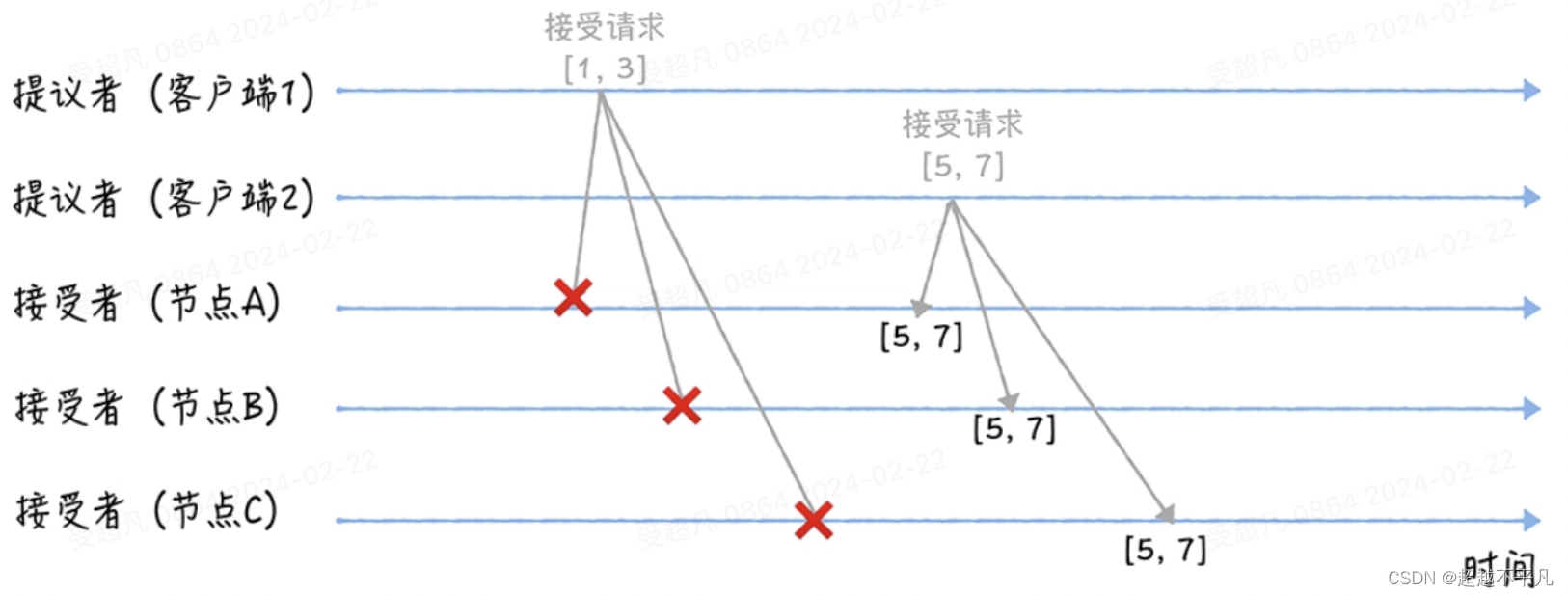
探索分布式强一致性奥秘:Paxos共识算法的精妙之旅
提到分布式算法,就不得不提 Paxos 算法,在过去几十年里,它基本上是分布式共识的代名词,因为当前一批常用的共识算法都是基于它改进的。比如,Fast Paxos 算法、Cheap Paxos、Raft 算法等。 由莱斯利兰伯特(L…...

使用 ES|QL 优化可观察性:简化 Kubernetes 和 OTel 的 SRE 操作和问题解决
作者:Bahubali Shetti 作为一名运营工程师(SRE、IT 运营、DevOps),管理技术和数据蔓延是一项持续的挑战。 简单地管理大量高维和高基数数据是令人难以承受的。 作为单一平台,Elastic 帮助 SRE 将无限的遥测数据&#…...

Docker 第十九章 : 阿里云个人镜像仓使用
Docker 第十九章 : 阿里云个人镜像仓使用 本章知识点: 如何创建镜像库,如何设置密码,如何登录与退出个人镜像仓,如何本地打镜像,如何将本地镜像推送到个人镜像库。 背景 在项目YapiDocker部署中,因读取mongo:latest 版本不一致,导致后续执行步骤的异常。遇到此场景…...

二、系统知识笔记-系统架构概述
一、系统架构定义 系统架构是指对一个系统的整体结构和组成部分进行描述和规划的过程。系统架构定义决定了系统的设计、开发和实施过程中的关键方向和决策。是系统的骨架和根基,支撑和链接各个部分,包括组件、连接件、约束规范以及指导这些内容设计与演…...

【高德地图】Android高德地图绘制标记点Marker
📖第4章 Android高德地图绘制标记点Marker ✅绘制默认 Marker✅绘制多个Marker✅绘制自定义 Marker✅Marker点击事件✅Marker动画效果✅Marker拖拽事件✅绘制默认 Infowindow🚩隐藏InfoWindow 弹框 ✅绘制自定义 InfoWindow🚩实现 InfoWindow…...
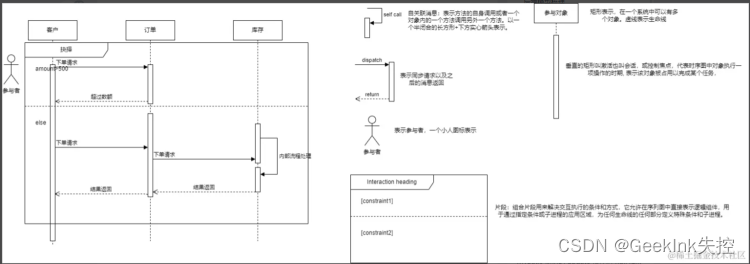
每天一个知识点 - 如何快速熟悉后端项目
入职一家新公司的时候,不可避免的就是接触到新公司的项目,有些项目一启动就是好几年,业务功能极其复杂,下面我总结几个方法让大家快速熟悉后端项目(图文结合) 用例图简析 用例是系统中的一个功能单元&…...
如何将cocos2d-x js打包部署到ios上 Mac M1系统
项目环境 cocos2d-x 3.13 xcode 12 mac m1 big sur 先找到你的项目 使用xcode软件打开上面这个文件 打开后应该是这个样子 执行编译运行就好了 可能会碰到的错误 在xcode11版本以上都会有这个错误,这是因为iOS11废弃了system。 将上面代码修改为 #if (CC_TARGE…...

pdffactory pro 8中文破解版
详细介绍 PdfFactory,PDF文档虚拟打印机,无须Acrobat即可创建Adobe PDF文件,创建PDF文件的方法比其他方法更方便和高效。支持将多个文档整合到一个PDF文件、增加字体和便签、PDF加密、去水印、压缩优化。 FinePrint,Windows虚拟…...

常用ADB命令整理已经ADB键盘输入
我们在测试Android app过程中 需要经常更换安装包的操作 熟练使用ADB命令可以提升测试效率 * 查看设备 adb devices ps这个命令是查看当前连接的设备, 连接到计算机的android设备或者模拟器将会列出显示 若有多台安卓设备,可以通过在adb后面加上 -s <设备id>…...
buuctf_N1BOOK_粗心的小李
题目: 看完题目,git下载文件?然后将.git文件传到线上环境?(which 会造成git泄露的安全威胁)<这个背景抱歉我不太了解哈,可能后续有补充> 这里主要记录做法过程: 工具…...
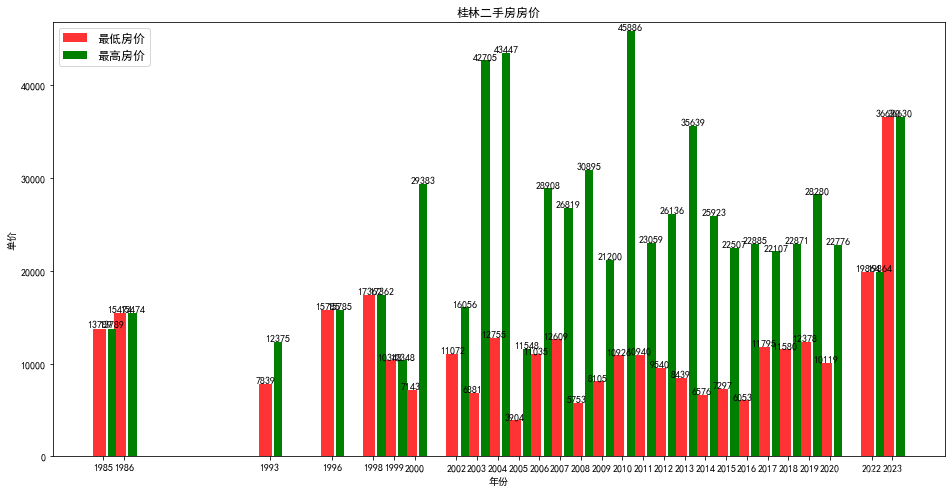
爬取链家二手房房价数据存入mongodb并进行分析
实验目的 1.使用python将爬虫数据存入mongodb; 2.使用python读取mongodb数据并进行可视化分析。 实验原理 MongoDB是文档数据库,采用BSON的结构来存储数据。在文档中可嵌套其他文档类型,使得MongoDB具有很强的数据描述能力。本节案例使用的…...
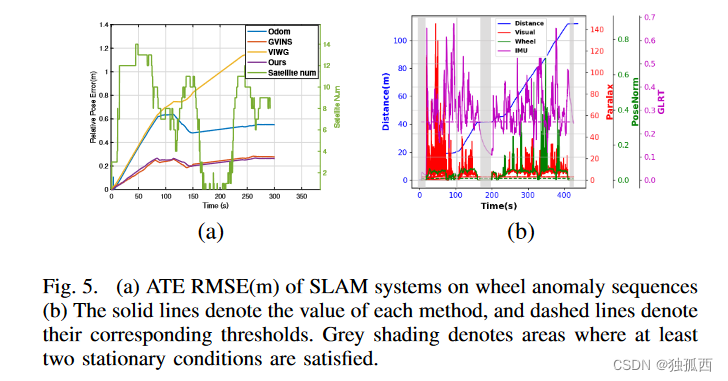
论文阅读:Ground-Fusion: A Low-cost Ground SLAM System Robust to Corner Cases
前言 最近看到一篇ICRA2024上的新文章,是关于多传感器融合SLAM的,好像使用了最近几年文章中较火的轮式里程计。感觉这篇文章成果不错,代码和数据集都是开源的,今天仔细读并且翻译一下,理解创新点、感悟研究方向、指导…...

一键获取电商平台商品信息,快速提高电商业务效率
阿里巴巴店铺所有商品API接口技术全解析 一、引言 在阿里巴巴这个全球领先的电商平台上,店铺所有商品API接口(item_search_shop)为开发者提供了一个便捷的途径,能够获取店铺的所有商品信息。通过这一接口,无论是数据…...

vue 中实现音视频播放进度条(满足常见开发需求)
由于开发需要,作者封装了一个音视频播放进度条的插件,支持 vue2 及 vue3 ,有需要的朋友可联系作者,下面是对该款插件的介绍。 插件默认样式👇(插件提供了多个配置选项,可根据自身需求进行个性化…...

【广度优先搜索】【网格】【割点】1263. 推箱子
作者推荐 视频算法专题 涉及知识点 广度优先搜索 网格 割点 并集查找 LeetCode:1263. 推箱子 「推箱子」是一款风靡全球的益智小游戏,玩家需要将箱子推到仓库中的目标位置。 游戏地图用大小为 m x n 的网格 grid 表示,其中每个元素可以是墙、地板或…...
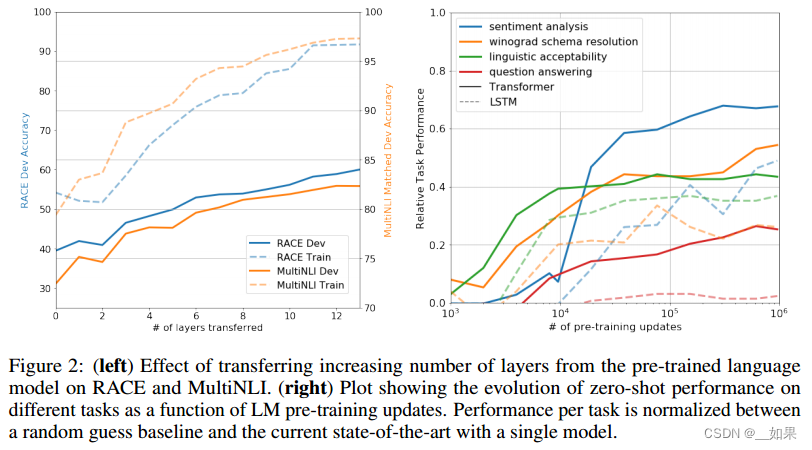
论文精读--GPT1
把transformer的解码器拿出来,在没有标号的大量文本数据上训练一个语言模型,来获得预训练模型,然后到子任务上微调,得到每个任务所需的分类器 Abstract Natural language understanding comprises a wide range of diverse tasks…...
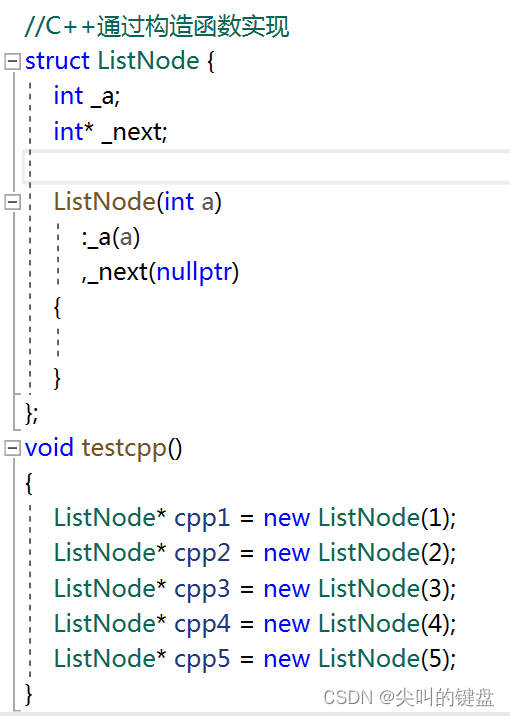
C/C++的内存管理(1)
内存管理 C与C的内存分布C语言中动态内存管理方式回顾C内存管理的方式 C与C的内存分布 我们学习C语言时就知道,储存不同的变量计算机会相应分配不同区块的内存。那为什么要把内存化为不同的区域呢?实质上是为了方便管理 下面我们来看看下面一道例题&…...

C 标准库 - <stdlib.h>
简介 <stdlib.h> 头文件定义了四个变量类型、一些宏和各种通用工具函数。 库变量 下面是头文件 stdlib.h 中定义的变量类型: 序号变量 & 描述1size_t2wchar_t3div_t4ldiv_t 库宏 下面是头文件 stdlib.h 中定义的宏: 序号宏 & 描述1…...

Python中回调函数的理解与应用
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站零基础入门的AI学习网站~。 目录 前言 回调函数的概念 回调函数的基本用法 回调函数的实现方式 1 使用函数 2 使用类方法 3 使用类实…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...
