B3623枚举排列
题目描述
今有 n 名学生,要从中选出 k 人排成一列拍照。
请按字典序输出所有可能的排列方式。
输入格式
仅一行,两个正整数 n,k。
输出格式
若干行,每行 k 个正整数,表示一种可能的队伍顺序。
输入输出样例
输入 #1复制
3 2
输出 #1复制
1 2 1 3 2 1 2 3 3 1 3 2
#include<bits/stdc++.h>
using namespace std;
int a[10],n,k;
bool b[10]={0},flag=0;
void dfs(int x,int n,int k)
{if(x==k)//到边界{for(int i=0;i<k;i++)//输出{cout<<a[i]<<" ";}cout<<endl;}for(int i=1;i<=n;i++)//从n个数中选{if(b[i]==1)continue;for(int j=0;j<x;j++)//找重复if(a[j]==i)flag=1;if(flag)continue;a[x]=i;b[i]=1;//标记dfs(x+1,n,k);a[x]=0;//回溯b[i]=0;//回溯*2}
}
int main()
{cin>>n>>k;dfs(0,n,k);//从0开始搜索return 0;
}
相关文章:

B3623枚举排列
题目描述 今有 n 名学生,要从中选出 k 人排成一列拍照。 请按字典序输出所有可能的排列方式。 输入格式 仅一行,两个正整数 n,k。 输出格式 若干行,每行 k 个正整数,表示一种可能的队伍顺序。 输入输出样例 输入 #1复制 …...

vuex怎么防止数据刷新丢失?
Vuex 是一个专为 Vue.js 应用程序开发的状态管理模式和库。它采用集中式存储管理应用的所有组件的状态,并以相应的规则保证状态以一种可预测的方式发生变化。为了防止 Vuex 中的数据在刷新时丢失,你可以采取以下策略: 持久化插件:…...
)
OpenGL ES 渲染 NV21、NV12、I420、YV12、YUYV、UYVY、I444(建议收藏)
本文主要讲解常见的 YUV 格式图像渲染方式,如果对 YUV 格式不是很熟悉的同学可以翻看旧文一文掌握 YUV 图像的基本处理,YUV 格式的介绍这里不再展开。 渲染 NV21、NV12 格式图像 NV21、NV12 可以看成同一种结构,区别只是 uv 的交错排列顺序不同。 渲染 NV21/NV12 格式图像…...

云计算的两地三中心和灾备介绍
两地三中心是指在不同的地理位置建立两个数据中心和一个灾备中心,其中一个数据中心为主数据中心,另一个数据中心为备用数据中心,灾备中心则用于备份数据和在主数据中心或备用数据中心发生故障或灾难时提供应急支持。 异地灾备则是指在不同的地…...

Spring Bean
Spring的配置方式 1、xml配置文件 2、基于注解的方式 3、基于Java的方式 Spring Bean的生命周期 1、通过构造器或工厂方法创建bean实例 2、为bean的属性赋值 3、调用bean的初始化方法 4、使用bean 5、当容器关闭时,调用bean的销毁方法 Spring inner beans …...

Linux的时间操作
当涉及到时间操作时,Linux提供了一系列函数和结构体来处理时间的获取、转换和操作。 time_t 别名 time_t 是 C/C 中用来表示时间的类型,通常被定义为整数类型。它通常用来存储从纪元(通常是1970年1月1日)到某一特定时间点之间的…...
2024-02-21 作业
作业要求: 复习课上内容 //已完成结构体字节对齐,64位没做完的做完,32位重新都做一遍,课上指定2字节对齐的做一遍,自己验证 //已完成两种验证大小端对齐的代码写一遍复习指针内容 //已完成完善顺序表已写出的…...

平台组成-监控服务
监控服务和其他服务不同,不是一个单一的微服务,准确来说是一个体系。每个微服务都集成了Actuator,通过Actuator对外提供微服务的运行状况。关于Actuator大家可以阅读这篇文章。《Spring boot——Actuator 详解》 其上是Micrometer&…...
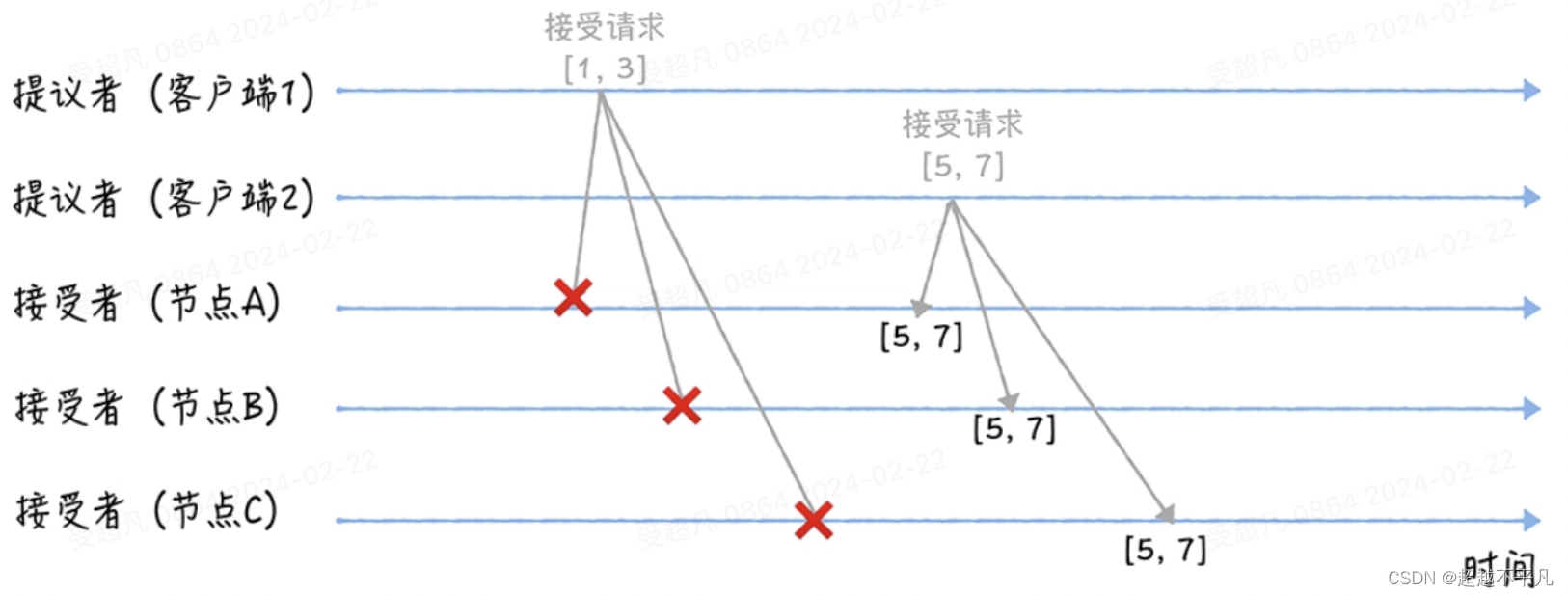
探索分布式强一致性奥秘:Paxos共识算法的精妙之旅
提到分布式算法,就不得不提 Paxos 算法,在过去几十年里,它基本上是分布式共识的代名词,因为当前一批常用的共识算法都是基于它改进的。比如,Fast Paxos 算法、Cheap Paxos、Raft 算法等。 由莱斯利兰伯特(L…...

使用 ES|QL 优化可观察性:简化 Kubernetes 和 OTel 的 SRE 操作和问题解决
作者:Bahubali Shetti 作为一名运营工程师(SRE、IT 运营、DevOps),管理技术和数据蔓延是一项持续的挑战。 简单地管理大量高维和高基数数据是令人难以承受的。 作为单一平台,Elastic 帮助 SRE 将无限的遥测数据&#…...

Docker 第十九章 : 阿里云个人镜像仓使用
Docker 第十九章 : 阿里云个人镜像仓使用 本章知识点: 如何创建镜像库,如何设置密码,如何登录与退出个人镜像仓,如何本地打镜像,如何将本地镜像推送到个人镜像库。 背景 在项目YapiDocker部署中,因读取mongo:latest 版本不一致,导致后续执行步骤的异常。遇到此场景…...

二、系统知识笔记-系统架构概述
一、系统架构定义 系统架构是指对一个系统的整体结构和组成部分进行描述和规划的过程。系统架构定义决定了系统的设计、开发和实施过程中的关键方向和决策。是系统的骨架和根基,支撑和链接各个部分,包括组件、连接件、约束规范以及指导这些内容设计与演…...

【高德地图】Android高德地图绘制标记点Marker
📖第4章 Android高德地图绘制标记点Marker ✅绘制默认 Marker✅绘制多个Marker✅绘制自定义 Marker✅Marker点击事件✅Marker动画效果✅Marker拖拽事件✅绘制默认 Infowindow🚩隐藏InfoWindow 弹框 ✅绘制自定义 InfoWindow🚩实现 InfoWindow…...
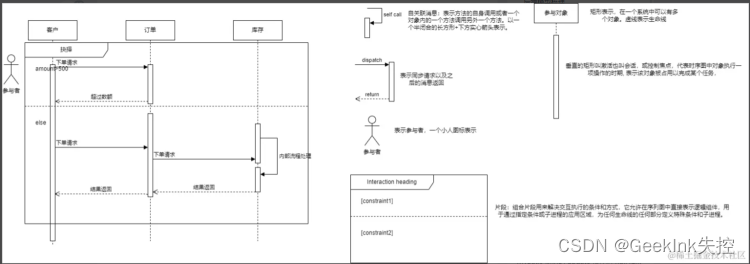
每天一个知识点 - 如何快速熟悉后端项目
入职一家新公司的时候,不可避免的就是接触到新公司的项目,有些项目一启动就是好几年,业务功能极其复杂,下面我总结几个方法让大家快速熟悉后端项目(图文结合) 用例图简析 用例是系统中的一个功能单元&…...
如何将cocos2d-x js打包部署到ios上 Mac M1系统
项目环境 cocos2d-x 3.13 xcode 12 mac m1 big sur 先找到你的项目 使用xcode软件打开上面这个文件 打开后应该是这个样子 执行编译运行就好了 可能会碰到的错误 在xcode11版本以上都会有这个错误,这是因为iOS11废弃了system。 将上面代码修改为 #if (CC_TARGE…...

pdffactory pro 8中文破解版
详细介绍 PdfFactory,PDF文档虚拟打印机,无须Acrobat即可创建Adobe PDF文件,创建PDF文件的方法比其他方法更方便和高效。支持将多个文档整合到一个PDF文件、增加字体和便签、PDF加密、去水印、压缩优化。 FinePrint,Windows虚拟…...

常用ADB命令整理已经ADB键盘输入
我们在测试Android app过程中 需要经常更换安装包的操作 熟练使用ADB命令可以提升测试效率 * 查看设备 adb devices ps这个命令是查看当前连接的设备, 连接到计算机的android设备或者模拟器将会列出显示 若有多台安卓设备,可以通过在adb后面加上 -s <设备id>…...
buuctf_N1BOOK_粗心的小李
题目: 看完题目,git下载文件?然后将.git文件传到线上环境?(which 会造成git泄露的安全威胁)<这个背景抱歉我不太了解哈,可能后续有补充> 这里主要记录做法过程: 工具…...
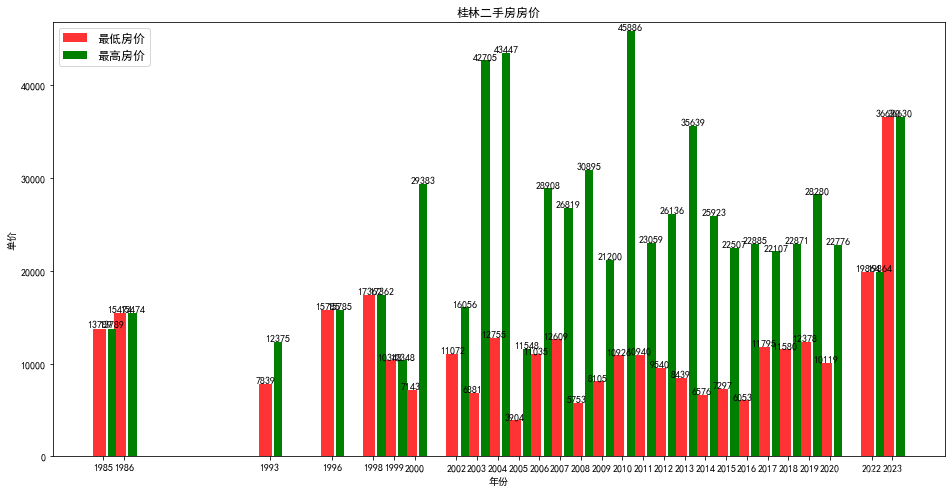
爬取链家二手房房价数据存入mongodb并进行分析
实验目的 1.使用python将爬虫数据存入mongodb; 2.使用python读取mongodb数据并进行可视化分析。 实验原理 MongoDB是文档数据库,采用BSON的结构来存储数据。在文档中可嵌套其他文档类型,使得MongoDB具有很强的数据描述能力。本节案例使用的…...
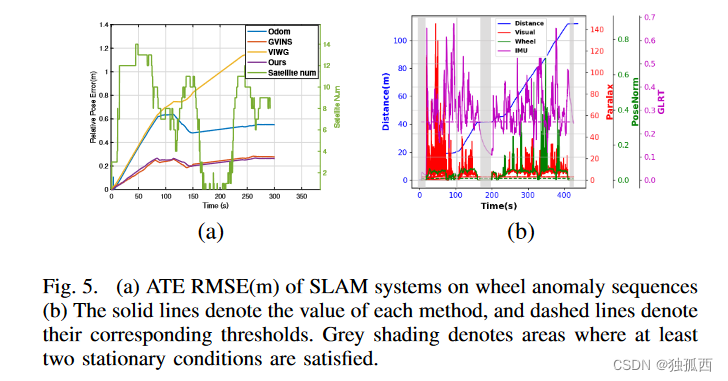
论文阅读:Ground-Fusion: A Low-cost Ground SLAM System Robust to Corner Cases
前言 最近看到一篇ICRA2024上的新文章,是关于多传感器融合SLAM的,好像使用了最近几年文章中较火的轮式里程计。感觉这篇文章成果不错,代码和数据集都是开源的,今天仔细读并且翻译一下,理解创新点、感悟研究方向、指导…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

2025-05-08-deepseek本地化部署
title: 2025-05-08-deepseek 本地化部署 tags: 深度学习 程序开发 2025-05-08-deepseek 本地化部署 参考博客 本地部署 DeepSeek:小白也能轻松搞定! 如何给本地部署的 DeepSeek 投喂数据,让他更懂你 [实验目的]:理解系统架构与原…...
