吴恩达deeplearning.ai:sigmoid函数的替代方案以及激活函数的选择
以下内容有任何不理解可以翻看我之前的博客哦:吴恩达deeplearning.ai专栏
文章目录
- 引入——改进下需求预测模型
- ReLU函数(整流线性单元 rectified linear unit)
- 线性激活函数(linear activation function)
- 激活函数的选择
- 实现方式
- 为什么需要激活函数
到现在为止,我们一直在隐藏层和输出层使用sigmoid函数作为激活函数,之所以我们这样做是因为我们创建了大量逻辑回归单元,并且要将它们串联起来。但在很多情况下,你使用其它的激活函数会使你的神经网络更加强大。
引入——改进下需求预测模型
让我们先看看之前的博客中见到过的需求预测例子:

在之前,我们将awareness这个神经元看作是一个逻辑回归,即要么意识到,要么没有意识到。但在很多情况下,awareness的情况并不会这么绝对,它们可能有些了解但不多,有可能很了解,也有可能已经开始病毒化传播了,如果此时仍然使用sigmoid函数就会降低神经网络模型的准确性。所以,我们不如改变为预测awareness的概率为多大,甚至是从0到无穷大的一个值(因为要考虑到病毒化传播的几何级增长),从而可以更精确地调整模型。
之前我们采用的sigmoid函数的数学公式为:
a 2 [ 1 ] = g ( w 2 [ 1 ] + b 2 [ 1 ] ) g ( z ) = 1 1 + e − z a_2^{[1]}=g(w_2^{[1]}+b_2^{[1]})\\ g(z)=\frac{1}{1+e^{-z}} a2[1]=g(w2[1]+b2[1])g(z)=1+e−z1
通过数学上的分析可以知道,g(z)一定是一个(0,1)之间的数,因此无法满足我们对于改变模型的需求。

ReLU函数(整流线性单元 rectified linear unit)
事实上,为了满足函数取值为0到无限大,我们可以采取非常简单的函数就是relu函数,数学公式为:
g ( z ) = m a x ( 0 , z ) g(z)=max(0,z) g(z)=max(0,z)

通俗点解释这个函数就是,如果z大于0,那么就是z本身,否则就是0。
线性激活函数(linear activation function)
和ReLU函数类似,只是允许了小于零的部分存在,在某些地方,可能会有人称呼它为没有使用激活函数(no activation function)(因为就是它本身,和没用一样),数学表达式为:
g ( z ) = z g(z)=z g(z)=z
以上三个可以说是迄今为止神经网络最常用的三个激活函数,在之后的博客中我们将讨论第四种激活函数Softmax,通过这些激活函数,你能构建功能强大的神经网络。但是问题来了,我们什么时候该使用何种激活函数呢。
激活函数的选择
事实上,关于激活函数的选择,只要你观察了特征向量X和标签Y,那么对于激活函数的选择将会十分地自然。
它主要取决于你输出层的标签。

具体来说,如果你正在处理Y为布尔值的问题,即二分类问题时,通常选择的就是sigmoid函数,原理在之前的章节中提到过,这也是非常自然的想法。
但如果你正在解决一些回归相关问题,那么你可能会选择其它的激活函数,例如股票预测,就建议使用线性激活函数,因为你对于输出值的范围要求在负无穷到正无穷之间。
最后,如果y只能取非负值,例如房子的价格等(总不能倒贴吧),就可以使用ReLU作为激活函数。
事实上,ReLU是神经网络中迄今为止使用的最广泛的激活函数。尽管我们早期使用了很多的sigmoid函数,但现在ReLU的应用比sigmoid多多了(除非你要解决的单纯是二分类问题)。
这是为什么呢?第一,ReLU的运算比sigmoid快多了,ReLU只需要一步判断便能得出结果,但是sigmoid既要求幂,又要取反等等。第二个重要原因是ReLU仅仅在图形的一个部分变平,而sigmoid有两个部分变平,一个函数在很多地方都很平时,会导致你在使用梯度下降的速度真的很慢;这也很好理解,假设你在预测一个二分类问题,结果输出的结果为0.8和0.9对于代价函数来说带来的修正都很小,而且越靠近正确答案时,这个修正越小,从而使速度降低了。

在下面这张w,b和成本函数的图中也可以看出,图中的很多地方都非常平坦,这意味着斜率近乎于0,这会阻碍梯度下降。而ReLU函数就没有这个问题。

下面补充下激活函数在代码中的实现方式
实现方式
就是在Dense函数中修改参数:
from dense.keras.layers import Dense
model = Sequential([Dense(units=25, activation = 'relu'),#layer1Dense(units=15, activation = 'relu'),#layer2Dense(units=1, activation = 'sigmoid')#layer3])
当然在别的情况下也有别的激活函数:
Dense(units=x, activation = 'linear')
激活函数的种类还有很多,例如tan h函数、LeakyReLU函数、swish函数等,这些函数一般使用范围就没那么广,可以自己了解。
为什么需要激活函数

还是这个需求预测模型,如果我们采用线性激活函数会如何呢?事实证明,这个神经网络将会变得和线性回归网络没有什么不同,所以这会破坏使用神经网络模型的全部目的。因为它将无法拟合比线性回归更加复杂的模型。让我们举个更简单的例子吧:

假设一个只有一个隐藏层,一个最终输出层,且每层只有一个神经元,特征向量也仅仅含有一个特征,这估计是最最最简单的神经网络了,假设所有的激活函数仍然使用线性激活函数,那么计算过程如上,那么 a [ 2 ] a^{[2]} a[2]就是上图所计算出来的线性函数,那么还不如使用线性回归模型呢。
如果你学过线性代数,那么你会知道这个结果源于:线性函数的线性组合仍然是线性函数。那么无论如何都无法创造出更加复杂的模型。
所以,对于任何一个神经网络而言,只使用线性激活函数那么模型的计算结果仍然等同于线性回归的结果。对于大部分神经网络,使用ReLU就足够了。
这篇博客把激活函数有关的内容详细介绍了一下,下一博客将介绍有关多分类问题的内容。
为了给读者你造成不必要的麻烦,博主的所有视频都没开仅粉丝可见,如果想要阅读我的其他博客,可以点个小小的关注哦。
相关文章:

吴恩达deeplearning.ai:sigmoid函数的替代方案以及激活函数的选择
以下内容有任何不理解可以翻看我之前的博客哦:吴恩达deeplearning.ai专栏 文章目录 引入——改进下需求预测模型ReLU函数(整流线性单元 rectified linear unit)线性激活函数(linear activation function)激活函数的选择实现方式为什么需要激活函数 到现在…...

Alias许可分析中的数据可视化
Alias许可分析中的数据可视化:引领企业洞察合规之道的明灯 在信息化时代,数据可视化已成为各行各业的重要工具,能够帮助用户直观地理解和分析复杂的数据。在Alias许可分析中,数据可视化同样发挥着至关重要的作用,为企…...

【计算机网络】数据链路层--以太网/MTU/ARP/RARP协议
文章目录 一、以太网1.以太网帧格式2.MAC地址3.局域网的转发原理 二、MTU1.什么是MTU2.MTU对IP协议的影响3.MTU对UDP影响4.MTU对于TCP协议的影响 三、ARP协议1.ARP协议的作用2.ARP数据报的格式3.ARP协议的工作流程 一、以太网 “以太网” 不是一种具体的网络, 而是一种技术标准…...
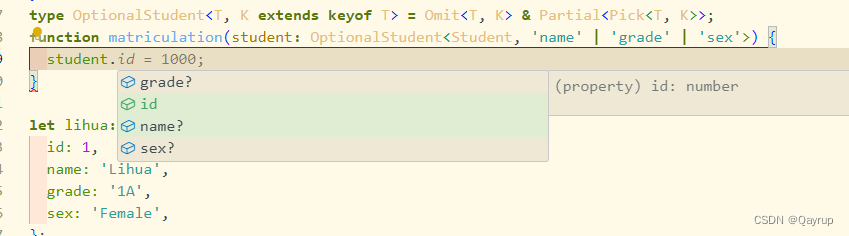
typescript使用解构传参
看下面这个函数 interface Student {id: number;name: string;class: string;sex: string;}function matriculation(student: Student) {//...}我们要调用它,就需要传递一个实现了Student约束的对象进去 interface Student {id: number;name: string;class: string;sex: string…...
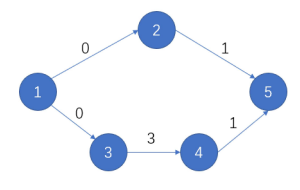
CSP-J 2023 复赛第4题:旅游巴士
【题目来源】https://www.luogu.com.cn/problem/P9751https://www.acwing.com/problem/content/description/5313/【题目描述】 小 Z 打算在国庆假期期间搭乘旅游巴士去一处他向往已久的景点旅游。 旅游景点的地图共有 n 处地点,在这些地点之间连有 m 条道路。 其中…...

JAVA算法和数据结构
一、Arrays类 1.1 Arrays基本使用 我们先认识一下Arrays是干什么用的,Arrays是操作数组的工具类,它可以很方便的对数组中的元素进行遍历、拷贝、排序等操作。 下面我们用代码来演示一下:遍历、拷贝、排序等操作。需要用到的方法如下 public…...

每日五道java面试题之spring篇(七)
目录: 第一题. 什么是Spring beans?第二题. 一个 Spring Bean 定义 包含什么?第三题. 如何给Spring 容器提供配置元数据?Spring有几种配置方式?第四题. Spring基于xml注入bean的几种方式?第五题:你怎样定义类的作用域…...
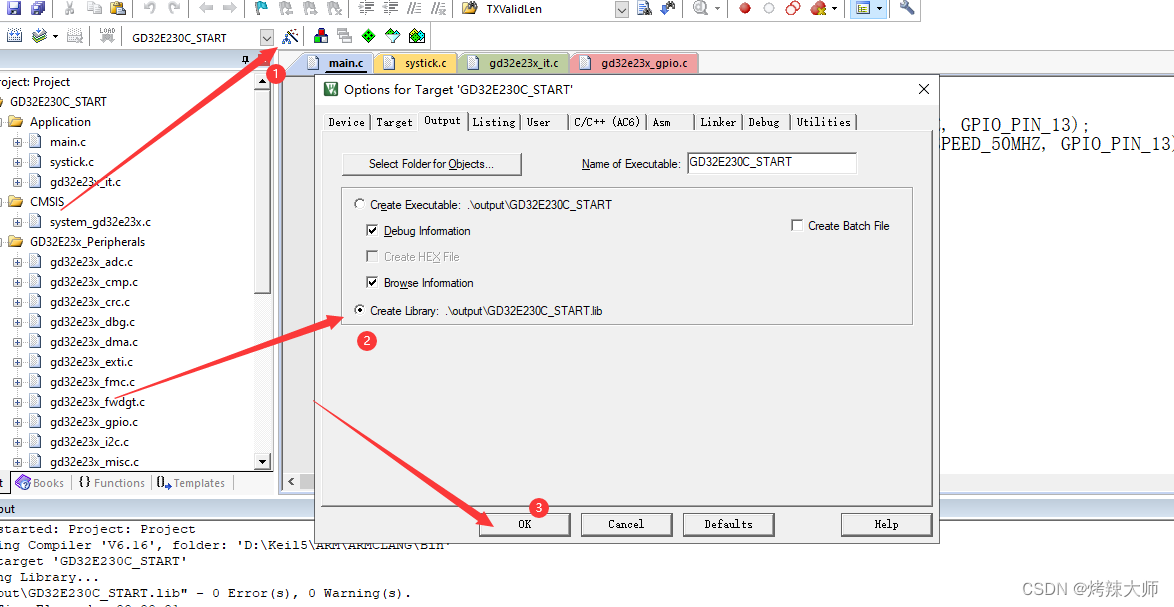
Keil编译GD32工程时找不到lib库文件
D:\Keil5\ARM\ARMCLANG\Bin\..\lib\armlib\mc_p.l:SELECTION_SCRIPT(2974): error: L6907E: Expected an expression. 问题 解决方法:因为编译器没有找到那个函数的代码,也就未解析了 其实问题很简单,把你的lib文件加进去,ok了…...

测试C#使用ViewFaceCore实现图片中的人脸遮挡
基于ViewFaceCore和DlibDotNet都能实现人脸识别,准备做个遮挡图片中人脸的程序,由于暂时不清楚DlibDotNet返回的人脸尺寸与像素的转换关系,最终决定使用ViewFaceCore实现图片中的人脸遮挡。 新建Winform项目,在Nuget包管理器中…...

2.21 Qt day2 菜单栏/工具栏/状态栏/浮动窗口、UI界面、信号与槽
思维导图 使用手动连接,将登录框中的取消按钮使用qt4版本的连接到自定义的槽函数中,在自定义的槽函数中调用关闭函数 将登录按钮使用qt5版本的连接到自定义的槽函数中,在槽函数中判断ui界面上输入的账号是否为"admin",…...
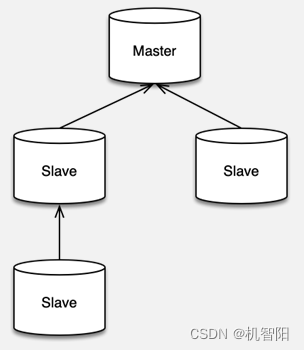
300分钟吃透分布式缓存-16讲:常用的缓存组件Redis是如何运行的?
Redis 基本原理 Redis 简介 Redis 是一款基于 ANSI C 语言编写的,BSD 许可的,日志型 key-value 存储组件,它的所有数据结构都存在内存中,可以用作缓存、数据库和消息中间件。 Redis 是 Remote dictionary server 即远程字典服务…...

上一篇文章补充:已经存在的小文件合并
对于HDFS上已经存在的大量小文件问题,有多种策略可以进行处理和优化: 1. **合并小文件**: - **使用Spark作业合并**:通过编写Spark程序读取小文件并调用repartition()或coalesce()函数重新分区数据,然后将合并后的…...

代码随想录训练营第三十期|第四十三天|动态规划 part05|1049. 最后一块石头的重量 II ● 494. 目标和 ● 474.一和零
1049. 最后一块石头的重量 II - 力扣(LeetCode) class Solution {public int lastStoneWeightII(int[] stones) {int sum 0;for (int n : stones) {sum n;}int target sum / 2;int[] dp new int[target 1];for (int i 0; i < stones.length; i…...

c++学习记录 string容器—字符串插入和删除
函数原型: string& insert(int pos,const char* s); //插入字符串string& insert(int pos,const string& str); //插入字符串string& insert(int pos,int n,char c); //在指定位置插入n个字符cstring&…...

【IEEE会议征稿】2024年第九届智能计算与信号处理国际学术会议(ICSP 2024)
2024年第九届智能计算与信号处理国际学术会议(ICSP 2024) 2024年第八届智能计算与信号处理国际学术会议(ICSP 2024)将在西安举行, 会期是2024年4月19-21日, 为期三天, 会议由西安科技大学主办。 欢迎参会&…...
【电机仿真】HFI算法脉振高频电压信号注入观测器-PMSM无感FOC控制
【电机仿真】HFI算法脉振高频电压信号注入观测器-PMSM无感FOC控制 文章目录 前言一、脉振高频电压注入法简介(注入在旋转坐标系的d轴)1.旋转高频电压(电流)注入法2.脉振高频电压注入法 二、高频注入理论1.永磁同步电机的高频模型2…...

Java学习——集合框架
Java集合框架(Java Collections Framework)是一套性能优良、使用方便的接口和类的集合,它位于java.util包下。这个框架包含了一系列集合接口的标准实现,比如列表、集合、队列,以及映射。使用这些集合,你可以…...
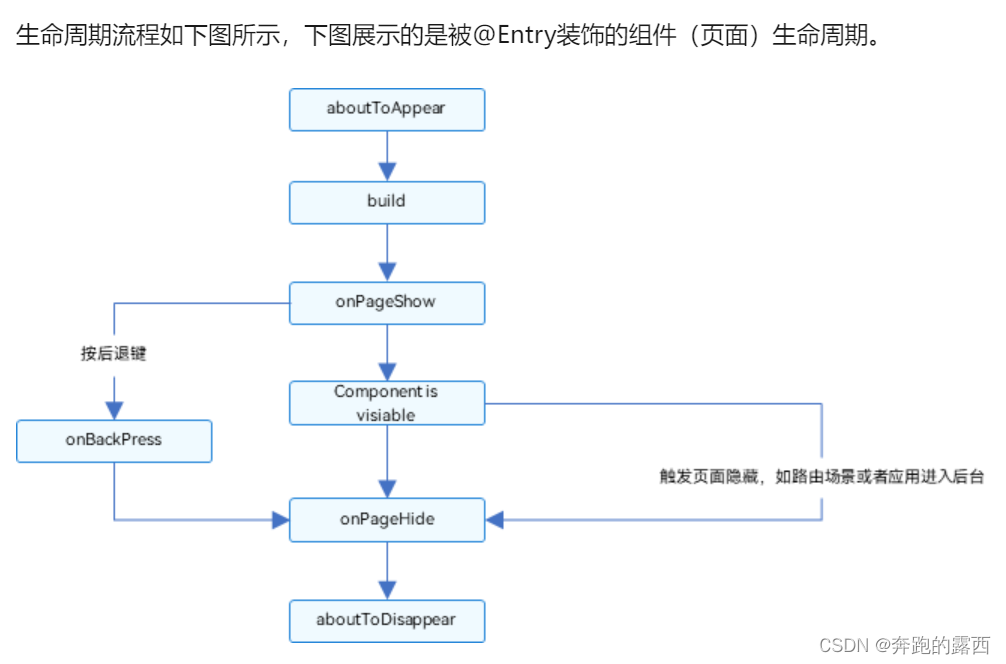
【鸿蒙 HarmonyOS 4.0】UIAbility、页面及组件的生命周期
一、背景 主要梳理下鸿蒙系统开发中常用的生命周期 二、UIAbility组件 UIAbility组件是一种包含UI界面的应用组件,主要用于和用户交互。 UIAbility组件是系统调度的基本单元,为应用提供绘制界面的窗口;一个UIAbility组件中可以通过多个页…...

jdk动态代理与CGLib动态代理
jdk动态代理 目标对象 package com.study;/*** 目标对象(被代理的对象)**/ public class Target implements TargetInf{public String name;public Target() {}public Target(String name) {this.name name;}public String buyCola (String name){Sys…...

Linux 命令行的世界 :4.操作文件和目录
此时此刻,我们已经准备好了做些真正的工作!这一章节将会介绍以下命令: • cp —复制文件和目录 • mv —移动/重命名文件和目录 • mkdir —创建目录 • rm —删除文件和目录 • ln —创建硬链接和符号链接 图形文件管理器能轻松地实现…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...
