【数据结构】时间复杂度与空间复杂度
目录
时间复杂度
空间复杂度
时间复杂度
算法的时间复杂度并不是指一个代码运行时间的快慢,因为在不同机器上运行的时间肯定不同,因此算法的时间复杂度指的是基本操作的执行次数,他是一个数学意义上的函数。这个函数并不是C语言中那种函数,而是一个数学函数,比如

显然是执行了N方+2N+10次,这个N方假设我们说他是F(N),也就是一个数学函数,那么这个F(N)就是上面这个算法的时间复杂度。但是实际上我们并不一定要计算精确的执行次数,而只需要大概执行次数,因为当N足够大的时候,F(N)的大小主要是由N方决定了,因此我们就可以用N方来近似这个表达式的值。 我们可以使用大O的渐进表示法。
大O渐进表示法的规则如下:
1、用常数1取代运行时间中的所有加法常数。比如要运行一万次是O(1),一亿次也是写作O(1),这是因为CPU的功能很强大,对于我们能写出来的这些常数,在CPU看来都一样,都是瞬间搞定。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。换句话说如果保留的最高阶数系数不是1,通通都写成系数是1,也就是说不管最终决定运算次数的项是2N,3N,1000N,使用大O渐进表示法都写作O(N),如果最后算出来运算次数是2的n-1次方,n-2次方等等,那么时间复杂度是O(2^n)
4.有些算法的时间复杂度存在最好、平均和最坏情况:最坏情况:任意输入规模的最大运行次数(上界)平均情况:任意输入规模的期望运行次数最好情况:任意输入规模的最小运行次数(下界)例如:在一个长度为N数组中搜索一个数据x最好情况:1次找到最坏情况:N次找到平均情况:N/2次找到。在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)
下面来计算一下冒泡排序的时间复杂度

执行的次数也就是for循环一共循环了多少次,可以看到第一次要比较n-1个,第二次要比较n-2个,第n-1次要比较1个,一共执行的次数就是这些全加起来,等差数列求和,因此一共是n(n-1)/2,最高次数是2次方,虽然有系数二分之一,但是要忽略掉,因此他的时间复杂度是O(n方)
注:只是在本例中执行次数就是循环次数,并不是说所有代码的执行次数都是循环次数
计算二分查找的时间复杂度
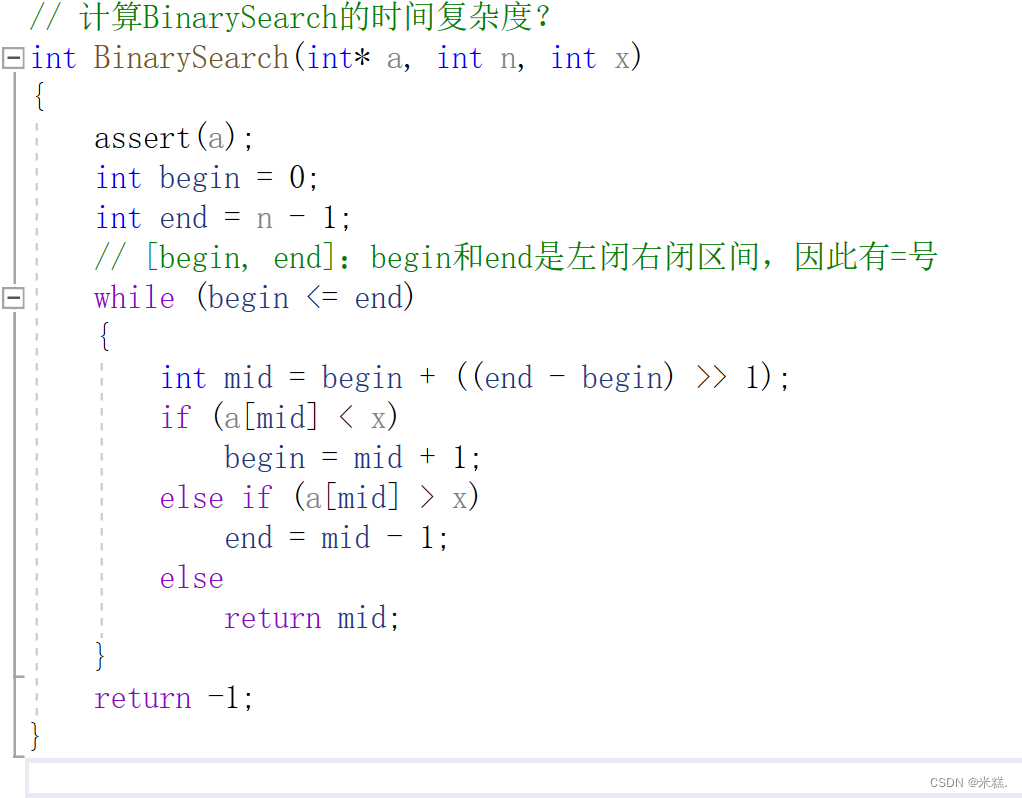
二分查找的思想就是一次去掉一半,实际上有可能是一次找到了,也有可能是找到剩下最后一个了也没找到,要计算复杂度,我们就要考虑最坏情况,最坏情况就是找到了剩下最后一个元素,这就是最后一次,不管最后剩下的这个元素是不是我们要找的元素,都不会再执行了,假设有n个数,找了x次最后剩下一个了,实际上x就是复杂度,那么x能不能用已知条件表示呢?N除了x个2变成了1,换句话说1乘上x个2也就是2的x次方等于n,x也就是以二为底n的对数,因此二分查找的时间复杂度是以二为底n的对数。
阶乘递归的时间复杂度

第一次调用Fac(N),而Fac(N)又会调用Fac(N-1),以此类推直到Fac(1)调用Fac(0),就开始一直返回了,因此实际基本语句执行了N+1次,时间复杂度是O(N)
把代码稍作修改,这次时间复杂度是多少?

仍然是Fac(N)调用Fac(N-1),Fac(N-1)调用Fac(N-2)以此类推直到Fac(1)调用Fac(0),但是在每次调用之前都有一个循环语句,在Fac(N)里执行了N次,在Fac(N-1)里执行了n-1次......在Fac(1)里执行了1次,因此基本操作一共执行了N(N+1)/2次,所以时间复杂度是O(N方)
计算斐波那契递归的时间复杂度

一生二,二生四,直到调用参数是2或者1的时候才可以返回值,因此右边的会先开始返回值,左边的后返回,最终形状大概是缺一块的三角形

形状类似这样
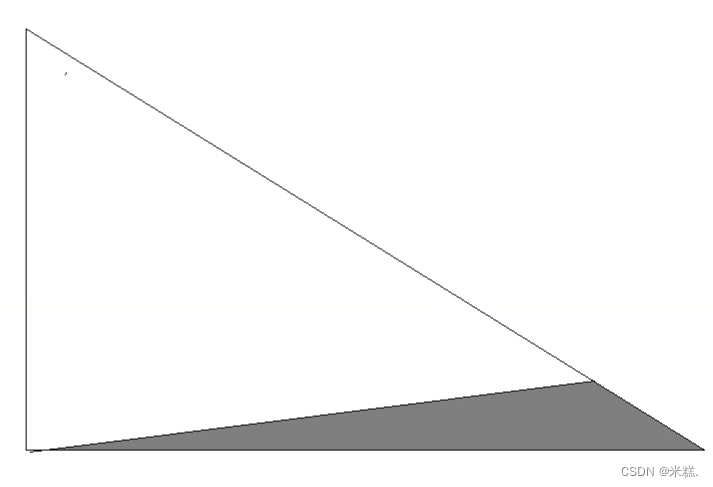
假设是一个满的三角形,那么最终应该有2的零次方一直加到2的N-2次方,这样一个等比数列求和,结果是2的N-1次方-1,实际上没有什么多项,还应该减去这个灰色的三角形,但是当N足够大的时候,实际上这个灰色三角形非常的小,可以忽略不计,因为复杂度考虑的是量级,是一个大约的数,因此我们就用这个完整三角形形状的个数来表示,因此斐波那契递归的时间复杂度是O(2^N)
空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度, 空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟实践复杂度类似,也使用大O渐进表示法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
计算冒泡排序的空间复杂度

在冒泡排序中,为了给传给我们的数组排序而额外创建的变量就只有end,exchange,i等等,也就是常数个,因此冒泡排序的空间复杂度是O(1)

创建了n+1个变量,因此空间复杂度是n+1,写作O(n+1),可能疑问就是这不是开辟了能放n+1个long long类型的空间吗,怎么就开辟变量了,这虽然是个指针,指针变量的名字实际上就相当于一个数组名,申请空间相当于是创建了一个数组,我可以使用[]操作符来访问这块空间的元素,比如fibArray[1]就访问了第二个元素,这不就是创建变量吗?
实际上我们在求空间复杂度的时候没有必要每次都紧扣定义创建的变量个数,一般来说就是关注开辟的空间能放多少个变量。

Fac(N)会调用Fac(N-1)以此类对直到Fac(1)调用Fac(0),一共调用了N+1次,每次里面创建了常数个变量,因此空间复杂度是O(N)

在上面计算过Fib的时间复杂度是O(2^N),也就是说执行了这个量级次基本操作,而每次基本操作创建的变量都是常数个,那是不是说Fib的空间复杂度也是O(2^N)呢?首先说答案:不是。在计算时间复杂度和空间复杂度的时候,我们应该遵循时间是一去不复返的,空间是可以重复利用的。
什么叫空间可以重复利用呢?
首先来说重复利用并不是共用,因为在调用完某个函数的时候,为他申请的栈帧就随之销毁了,何谈共用?
比如有这样一段代码

我们发现这两个变量的地址是相同的,这是因为我们在主函数里面调用了这两个函数,先调用Func1,于是为他开辟了一块栈帧,里面有变量a
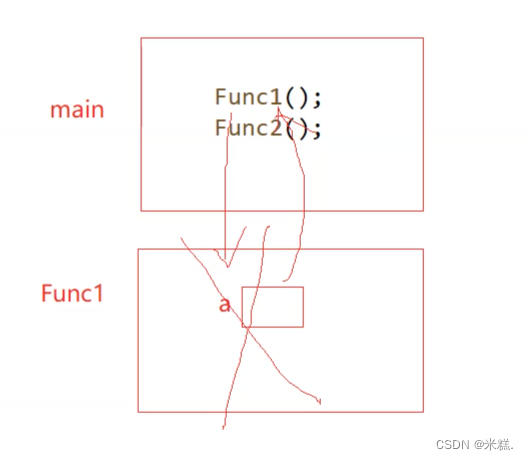
Func1调用完成之后,为他开辟的栈帧就被换给了操作系统,俗称栈帧被销毁,然后就开始调用Func2,也要为他开辟一块栈帧,前面通过打印地址我们知道这两个变量的地址是相同的,也就是说为Func2开辟的栈帧也是同一块。这就是空间的重复利用。
再回到Fib函数的空间复杂度计算
假设我们刚上来调用的是Fib(5)

计算这种递归函数的空间复杂度主要就是考虑开辟的栈帧是什么情况,比如我们刚上来调用的是Fib(5),Fib(5)为了得到返回值,就要调用Fib(4)和Fib(3),那问题来了,先后给Fib(4)和Fib(3)开辟栈帧吗?当然不是,先调用的是Fib(4),Fib(4)都还没返回呢,那必然不能调用Fib(3),那就不能为Fib(3)开辟栈帧,而是继续执行Fib(4),而Fib(4)会调用Fib(3)和Fib(2),先调用的是Fib(3),Fib(3)为了得到返回值就会调用Fib(2)和Fib(1),先调用的是Fib(2),此时有返回值了,在返回之后为Fib(2)申请的这快栈帧就可以还给操作系统了,有了返回值Fib(2)就算执行完了,那就可以接着调用Fib(1),从而又要为Fib(1)开辟一块栈帧,这块栈帧和刚才Fib(2)申请的那块是同一块,也能得到一个返回值并把这块栈帧销毁,这样Fib(3)就有值了,就能调用倒数第二行的Fib(2)了,于是为他申请一块栈帧,这快栈帧和刚才调用完Fib(3)被销毁的那块是同一块栈帧,以此类推,最终实际上就只申请了4块栈帧。
于是调用Fib(N)就申请了N-1块栈帧,因为同层的都在重复利用同一块空间,因此Fib的空间复杂度是O(N)。
相关文章:

【数据结构】时间复杂度与空间复杂度
目录 时间复杂度 空间复杂度 时间复杂度 算法的时间复杂度并不是指一个代码运行时间的快慢,因为在不同机器上运行的时间肯定不同,因此算法的时间复杂度指的是基本操作的执行次数,他是一个数学意义上的函数。这个函数并不是C语言中那种函数&…...

分别使用js与jquery写 单击按钮时出现内容 点击删除按钮不会再向下出现
HTML部分 <body><button id"btn">单击我</button><button id"delAll">删除所有事件</button><div id"test"></div> </bady>jQuery代码 <script type"text/JavaScript" src"…...
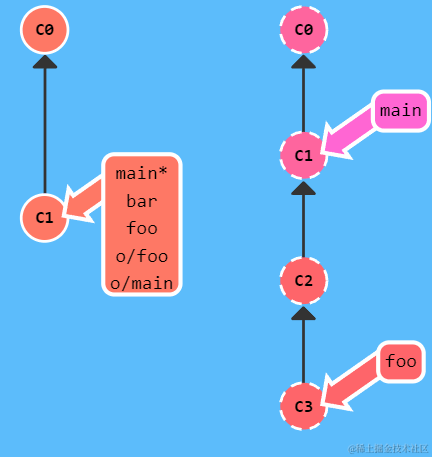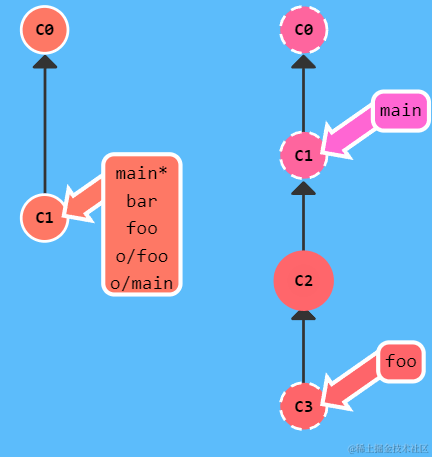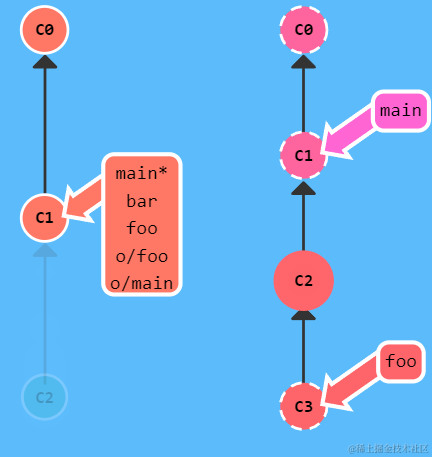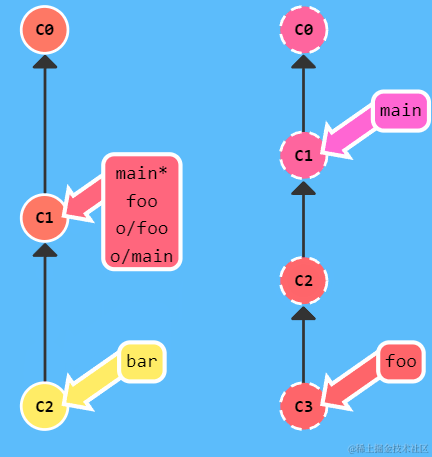
【Git】Git命令的学习与总结
本文实践于 Learn Git Branching 这个有趣的 Git 学习网站。在该网站,可以使用 show command 命令展示所有可用命令。你也可以直接访问网站的sandbox,自由发挥。 一、本地篇 基础篇 git commit git commit将暂存区(staging areaÿ…...

前端工程化面试题 | 18.精选前端工程化高频面试题
🤍 前端开发工程师、技术日更博主、已过CET6 🍨 阿珊和她的猫_CSDN博客专家、23年度博客之星前端领域TOP1 🕠 牛客高级专题作者、打造专栏《前端面试必备》 、《2024面试高频手撕题》 🍚 蓝桥云课签约作者、上架课程《Vue.js 和 E…...

大公司的工程师是怎么废掉的...
大家好,我是砖一。 此文作者以嵌入式工程师为基本视角,细说了从初阶到高阶工程师的资质需求,并提示工程师职业道路上的陷阱。可供参考。 一,基础知识 一个嵌入式工程师,很多都是从51单片机或者STM32单片机开始&…...

将yolov8权重文件转为onnx格式并在c#中使用
yolo模型转ONNX 在yolov8中,我们将训练结果的.pt权重文件转换为onnx格式只需要使用ultralytics库中的YOLO类,使用pip安装ultralytics库,然后执行下面python代码 from ultralytics import YOLO# 加载YOLOv8模型 model YOLO("best.pt&q…...

在Spring Boot启动时禁止自动配置数据源相关的组件、@SpringBootApplication
一、SpringBootApplication(exclude {DataSourceAutoConfiguration.class})注解 在Spring Boot启动时禁止自动配置数据源相关的组件。 SpringBootApplication(exclude {DataSourceAutoConfiguration.class})注解的使用案例 这个注解通常应该写在微服务项目的主启动类上&…...

程序人生:不积跬步无以致千里
程序人生 癸卯年冬月,往渭南韩城,拜访司马迁祠。入门攀爬而上,至人有困乏之时,抬头现:高山仰止。归路下山,始现三官洞,遥想西汉时三官洞,出口处刻意再拜别:高山仰止。泪…...

通过二叉树例题深入理解递归问题
目录 引入: 例1:二叉树的前序遍历: 例2: N叉树的前序遍历: 例3:二叉树的最大深度: 例4:二叉树的最小深度 例5:N叉树的最大深度: 例6:左叶子…...

【Android 协程常见用法】
我们这里只讲解一下,协程在Android项目中常见用法,原理知识不在进行说明了。 依赖 lifecycleScope只能在Activity、Fragment中使用,会绑定Activity和Fragment的生命周期。依赖库: implementation androidx.lifecycle:lifecycle…...
python 进程笔记一 (概念+示例代码)
1. 进程的概念 进程是资源分配的最小单位,也是线程的容器,线程(python 线程 (概念示例代码))是CPU调度的基本单位,一个进程包括多个线程。 程序:例如xxx.py是一个程序 进程…...

各中间件数据库默认访问端口总结
说明 在生态丰富的开发环境下,我们常常需要接触很多中间件产品,中间件默认的连接端口以及可视化ui访问端口也时不时的需要用到,这里循序渐进做好登记,以备查阅! 中间件/数据库名称默认端口管理台端口默认账号密码rabbi…...

鲲鹏arm64架构下安装KubeSphere
鲲鹏arm64架构下安装KubeSphere 官方参考文档: https://kubesphere.io/zh/docs/quick-start/minimal-kubesphere-on-k8s/ 在Kubernetes基础上最小化安装 KubeSphere 前提条件 官方参考文档: https://kubesphere.io/zh/docs/installing-on-kubernetes/introduction/prerequi…...

python 函数-02-返回值注释格式
01 函数返回值 1)python中函数可以没有返回值,也可以有通过return的方式 – 【特殊性,区别于java c#等】 2)返回值可以是一个或者多个,多个时通过逗号隔开 – 【特殊性,区别于java c#等】 3)多…...
【前端素材】推荐优质后台管理系统Upcube平台模板(附源码)
一、需求分析 后台管理系统在多个层次上提供了丰富的功能和细致的管理手段,帮助管理员轻松管理和控制系统的各个方面。其灵活性和可扩展性使得后台管理系统成为各种网站、应用程序和系统不可或缺的管理工具。 当我们从多个层次来详细分析后台管理系统时࿰…...
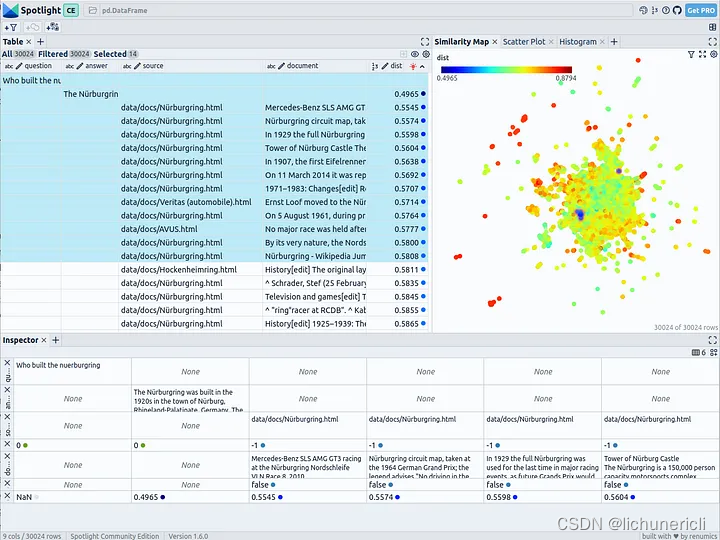
可视化 RAG 数据 — 用于检索增强生成的 EDA
原文地址:Visualize your RAG Data — EDA for Retrieval-Augmented Generation 2024 年 2 月 8 日 Github:https://github.com/Renumics/rag-demo/blob/main/notebooks/visualize_rag_tutorial.ipynb 为探索Spotlight中的数据,我们使用Pa…...

数学建模论文、代码百度网盘链接
1.[2018中国大数据年终总决赛冠军] 金融市场板块划分与轮动规律挖掘与可视化问题 2.[2019第九届MathorCup数模二等奖] 数据驱动的城市轨道交通网络优化策略 3.[2019电工杯一等奖] 露天停车场停车位的优化设计 4.[2019数学中国网络数模一等奖] 基于机器学习的保险业数字化变革…...

mysql 迁移-data目录拷贝方式
背景:从服务器进水坏掉,50多G的数据库要重新做主从,但以导入导出的方式太慢,简直是灾难性的,一夜都没好,只好想到了拷贝mysql数据文件的方式 拷贝的数据文件的前提 1.数据库版本必需一致(可以…...
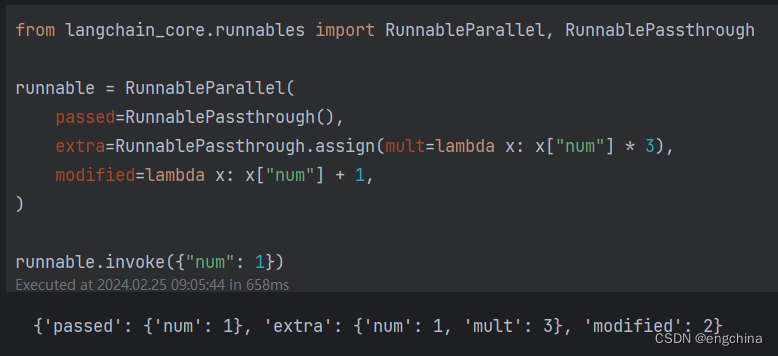
学习 LangChain 的 Passing data through
学习 LangChain 的 Passing data through 1. Passing data through2. 示例 1. Passing data through RunnablePassthrough 允许不改变或添加额外的键来传递输入。这通常与 RunnableParallel 结合使用,将数据分配给映射中的新键。 RunnablePassthrough() 单独调用&…...
C# OpenVINO PaddleSeg实时人像抠图PP-MattingV2
目录 效果 项目 代码 下载 C# OpenVINO 百度PaddleSeg实时人像抠图PP-MattingV2 效果 项目 代码 using OpenCvSharp; using Sdcb.OpenVINO; using System; using System.Diagnostics; using System.Drawing; using System.Security.Cryptography; using System.Text; us…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...
