通过二叉树例题深入理解递归问题
目录
引入:
例1:二叉树的前序遍历:
例2: N叉树的前序遍历:
例3:二叉树的最大深度:
例4:二叉树的最小深度
例5:N叉树的最大深度:
例6:左叶子之和:
例7:翻转二叉树:
例8: 路径总和:
例9:路径总和II:
例10:二叉树展开为链表:
引入:
递归是一种在函数定义中使用函数自身的方法。它是一种常见的编程技巧,用于解决可以被分解为相同问题的子问题的问题。递归函数通常包含两个部分:基本情况和递归情况。
基本情况是指递归函数停止调用自身的条件。当满足基本情况时,递归函数将不再调用自身,而是返回一个特定的值或执行特定的操作。
递归情况是指递归函数调用自身解决更小规模的子问题。通过不断地调用自身,递归函数可以将原始问题分解为更小的子问题,直到达到基本情况。
让我们再看二叉树的遍历,其实它的结构大概是这样(基本框架):
public void traverse(TreeNode root) {//前序遍历的位置traverse(root.left);//中序遍历的位置traverse(root.right);//后续遍历的位置}你或许会认为前中后续遍历不过就是要操作的代码位于这三个不同的位置而已,其实不然。我们抛开操作代码不谈,就只看这段代码,你就会发现他的主要遍历过程是这样:
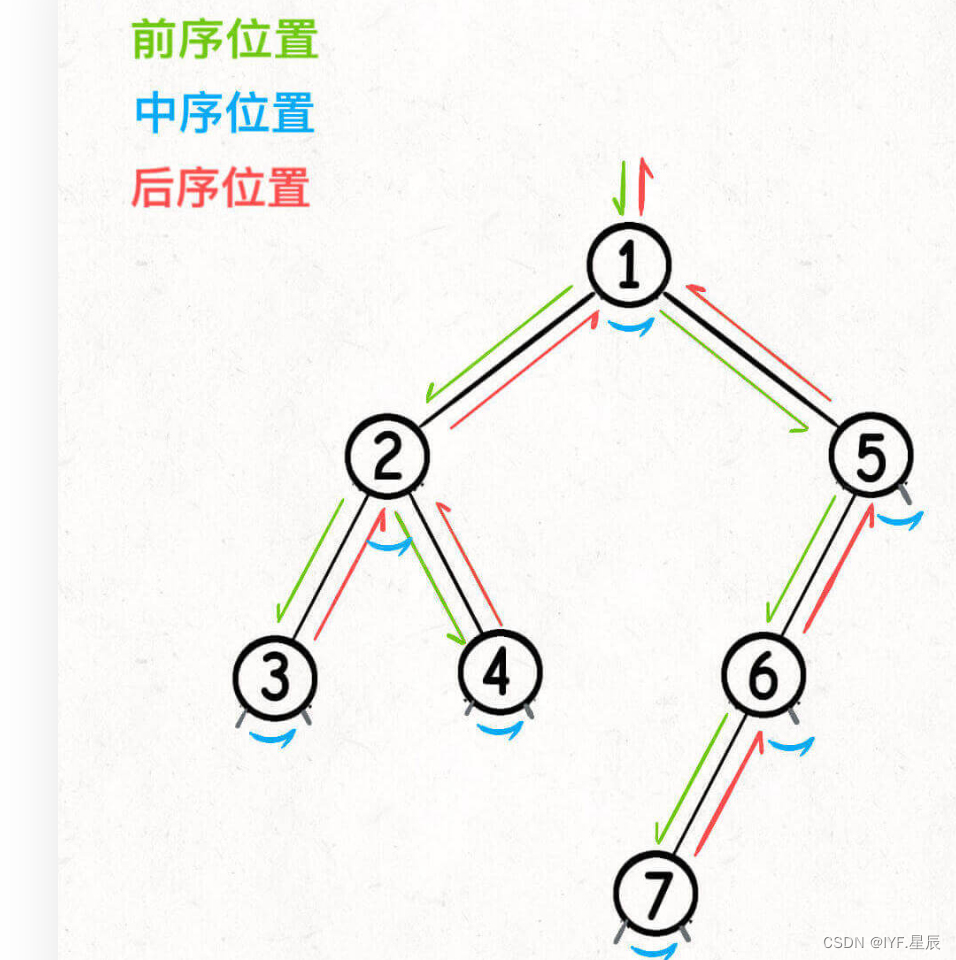
只不过我们在其遍历的过程中对某个节点进行了不同的操作罢了。如前序遍历,我们按照这个过程进入二叉树的遍历(绿->蓝->红),由于我们是在遍历前加入不同的操作,也就是按照:
①->②->③->④->⑤->⑥->⑦分别进行各项操作,前中后序是遍历二叉树过程中处理每一个节点的三个特殊时间点。 二叉树的问题,大致就是让你在这三个不同的时间节点注入巧妙的代码逻辑,来达成各项操作。关键要注意我们要在每个节点做什么,实施怎样的操作来完成我们的目标。通过递归将一个大的二叉树问题转化为一个个子树问题,直到不可再分就结束。
前序位置的代码在刚刚进入一个二叉树节点的时候执行;
后序位置的代码在将要离开一个二叉树节点的时候执行;
中序位置的代码在一个二叉树节点左子树都遍历完,即将开始遍历右子树的时候执行。
例1:二叉树的前序遍历:
题目:给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
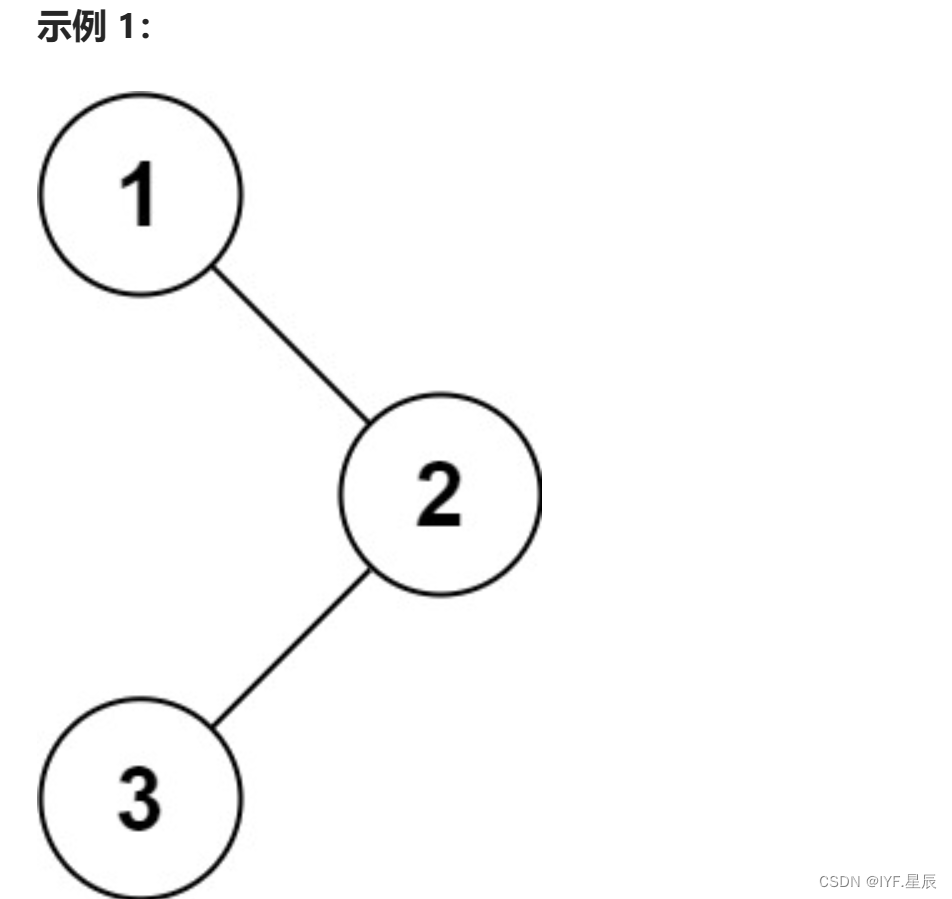
输入:root = [1,null,2,3] 输出:[1,2,3]
题目链接:144. 二叉树的前序遍历 - 力扣(LeetCode)
题解:通过联系二叉树的遍历过程,前序遍历就是让我们在框架前将该节点加入到list中
class Solution {List<Integer> list = new LinkedList<>();//用于存储遍历的信息public List<Integer> preorderTraversal(TreeNode root) {//递归的结束条件if(root == null){return list;}list.add(root.val);//根据框架,我们将该节点加入到list中preorderTraversal(root.left);preorderTraversal(root.right);return list;}
}二叉树的中后序遍历也是一样,将list分别放到框架中间和后面
例2: N叉树的前序遍历:
注:由于N叉树(不止包含左右子节点,可能有多个)的特性,其没有中序遍历,其大致框架是:
public void traverse(TreeNode root){if(root == null){return ;}//前序遍历的位置for(Node child : root.children){traverse(child);}//后序遍历的位置}题目:
给定一个 n 叉树的根节点 root ,返回 其节点值的 前序遍历 。
n 叉树 在输入中按层序遍历进行序列化表示,每组子节点由空值 null 分隔(请参见示例)。
题目链接:589. N 叉树的前序遍历 - 力扣(LeetCode)
题解:
class Solution {List<Integer> res = new LinkedList<Integer>();//用于存储二叉树的节点信息public List<Integer> preorder(Node root) {traverse(root);return res;}void traverse(Node root){if(root == null){return ;}res.add(root.val);for(Node child : root.children){traverse(child);}}
}例3:二叉树的最大深度:
题目:
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
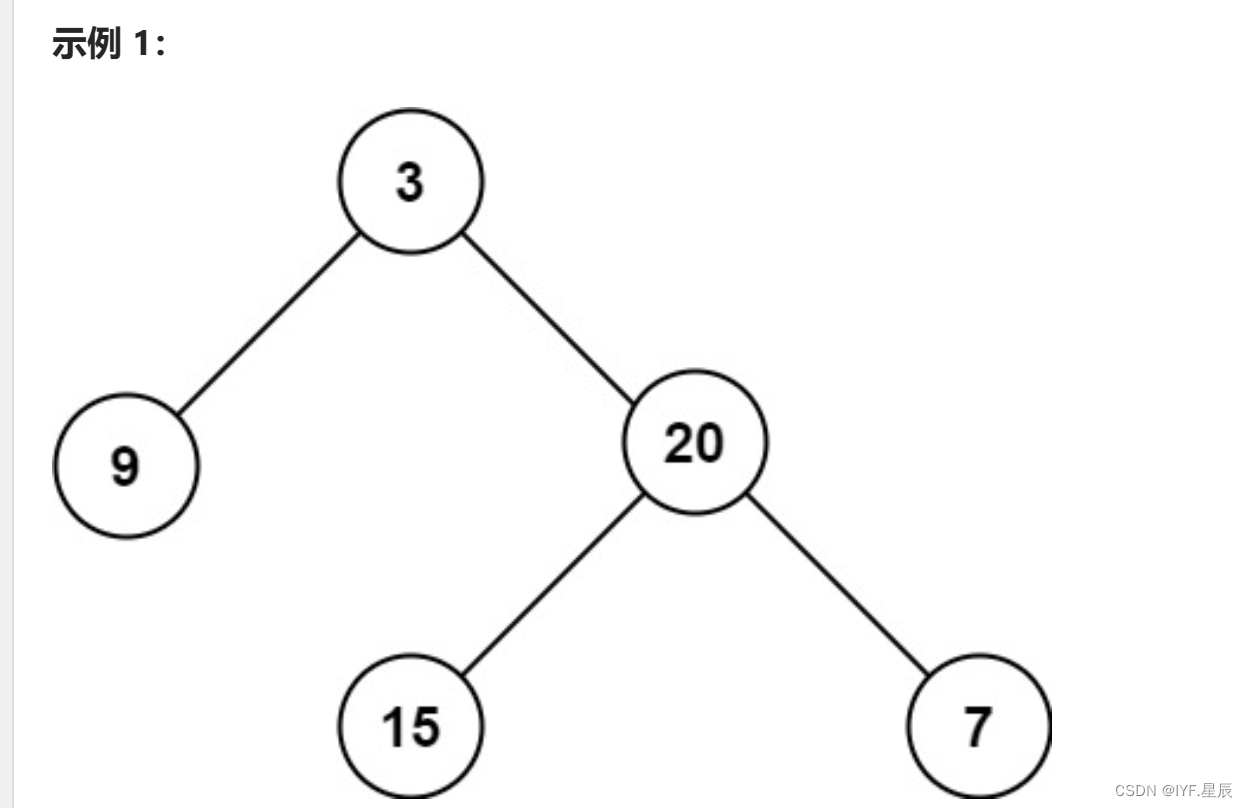
输入:root = [3,9,20,null,null,15,7] 输出:3
题目链接:104. 二叉树的最大深度 - 力扣(LeetCode)
法一:通过二叉树的遍历将其转化为左右子树的最大深度+1(自身)的方式进行求解:
class Solution {public int maxDepth(TreeNode root) {if(root == null){return 0;}int leftMax = maxDepth(root.left);//得到左树的最大深度int rightMax = maxDepth(root.right);//得到右树的最大深度return 1 + Math.max(leftMax,rightMax);//返回左右子树中的最大深度+1}
}我们不进入递归理解,而是从该函数的定义出发,maxDepth这个方法就是求树的最大深度,那是不是按照上面的思路我们照搬,先求左子树的最大深度,在求左子树的最大深度,然后从中去最大+1就行了。 或者按照上述的二叉树遍历过程理解:将这颗树不断分解(后序遍历),直到其分解成叶子节点,当它为空时,返回左右子树中的最大+1,在从最小的子树出发,不断往上进行比较,求最值+1---》最终得到我们的结果

法二:迭代思想,通过前序遍历记录最大深度,后续遍历来减少最大深度,同时不断记录最大深度的值:
class Solution {int ret = 0;//不断刷新最大深度的值int depth = 0;//记录深度public void traverse(TreeNode root){if(root == null){return ;}depth++;//在前序遍历时记录深度不断增加ret = Math.max(depth,ret);//同时刷新最大值traverse(root.left);traverse(root.right);depth--;//后续遍历时记录深度减少}public int maxDepth(TreeNode root) {traverse(root);return ret;}
}例4:二叉树的最小深度
题目:
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。说明:叶子节点是指没有子节点的节点。
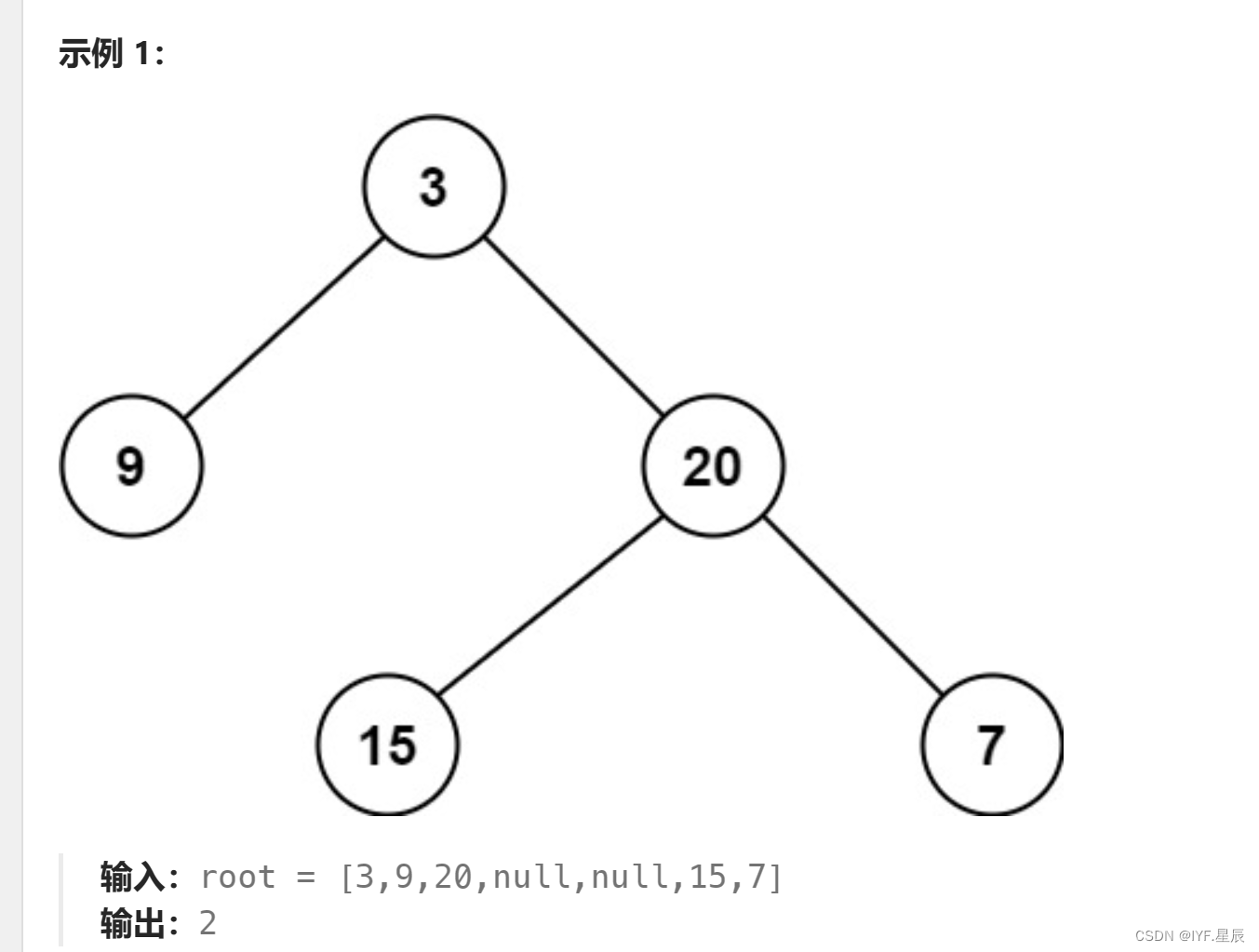
题目链接:111. 二叉树的最小深度 - 力扣(LeetCode)
题解:
法一:分解问题,不断求左右子树最小值:
// 「分解问题」的递归思路
class Solution2 {public int minDepth(TreeNode root) {// 基本情况:如果节点为空,返回深度为0if (root == null) {return 0;}// 递归计算左子树的最小深度int leftDepth = minDepth(root.left);// 递归计算右子树的最小深度int rightDepth = minDepth(root.right);// 特殊情况处理:如果左子树为空,返回右子树的深度加1if (leftDepth == 0) {return rightDepth + 1;}// 特殊情况处理:如果右子树为空,返回左子树的深度加1if (rightDepth == 0) {return leftDepth + 1;}// 计算并返回最小深度:左右子树深度的最小值加1return Math.min(leftDepth, rightDepth) + 1;}
}法二:迭代思想:与最小深度类似,但这里需要多一个判断是否是叶子节点,是叶子节点是我们才刷新最小值,不然开始就是最小值后续不会在改变,小细节,开始就定义一个极大值,为后续的找最小值做准备
class Solution {int depth = 0;int res = Integer.MAX_VALUE;public void traverse(TreeNode root){if(root == null){return ;}depth++;if(root.left == null && root.right == null){res = Math.min(res,depth);}traverse(root.left);traverse(root.right);depth--;}public int minDepth(TreeNode root) {if(root == null){return 0;}traverse(root);return res;}
}例5:N叉树的最大深度:
题目:
给定一个 N 叉树,找到其最大深度。
最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。
N 叉树输入按层序遍历序列化表示,每组子节点由空值分隔(请参见示例)。
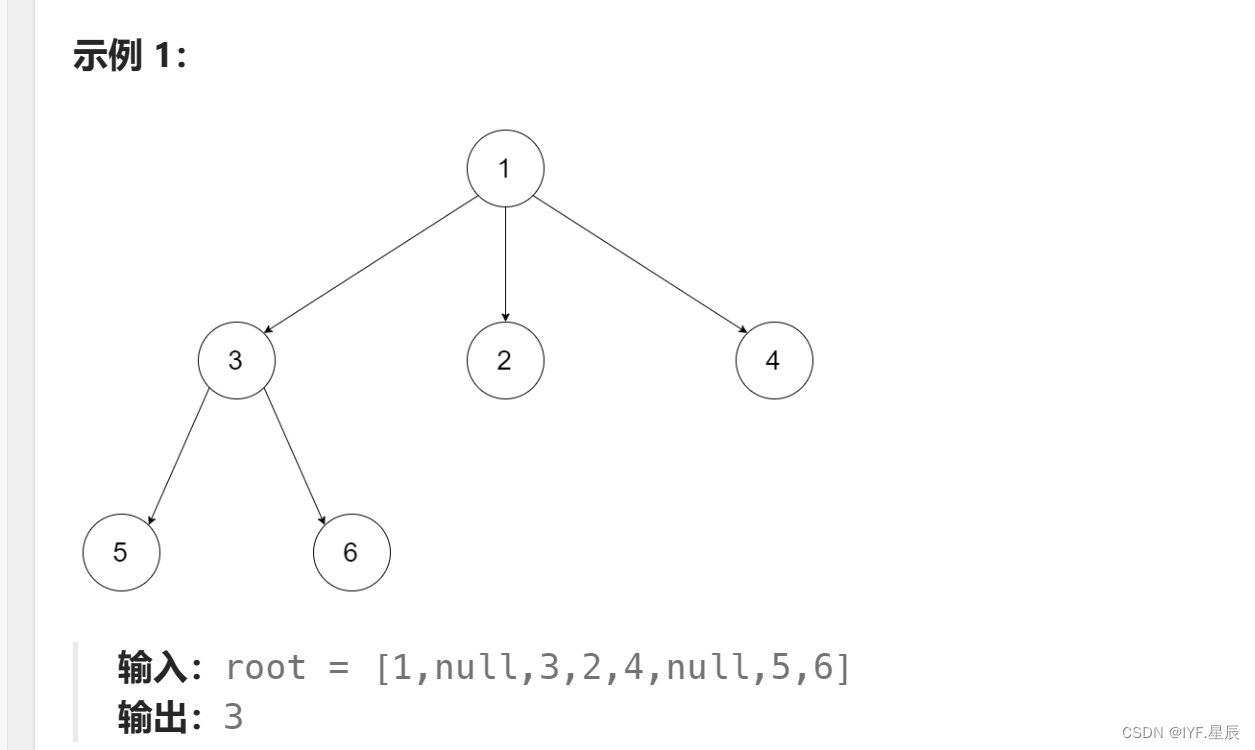
题目链接:559. N 叉树的最大深度 - 力扣(LeetCode)
题解:与二叉树的最大深度基本一致,就是要遍历所有子树:
class Solution {int res = 0;//记录最大值int depth = 0;//记录深度public int maxDepth(Node root) {if(root == null){return 0;}traverse(root);return res;}public void traverse(Node root){depth++;res = Math.max(res,depth);for(Node child : root.children){traverse(child);}depth--;}
}例6:左叶子之和:
题目:给定二叉树的根节点 root ,返回所有左叶子之和。
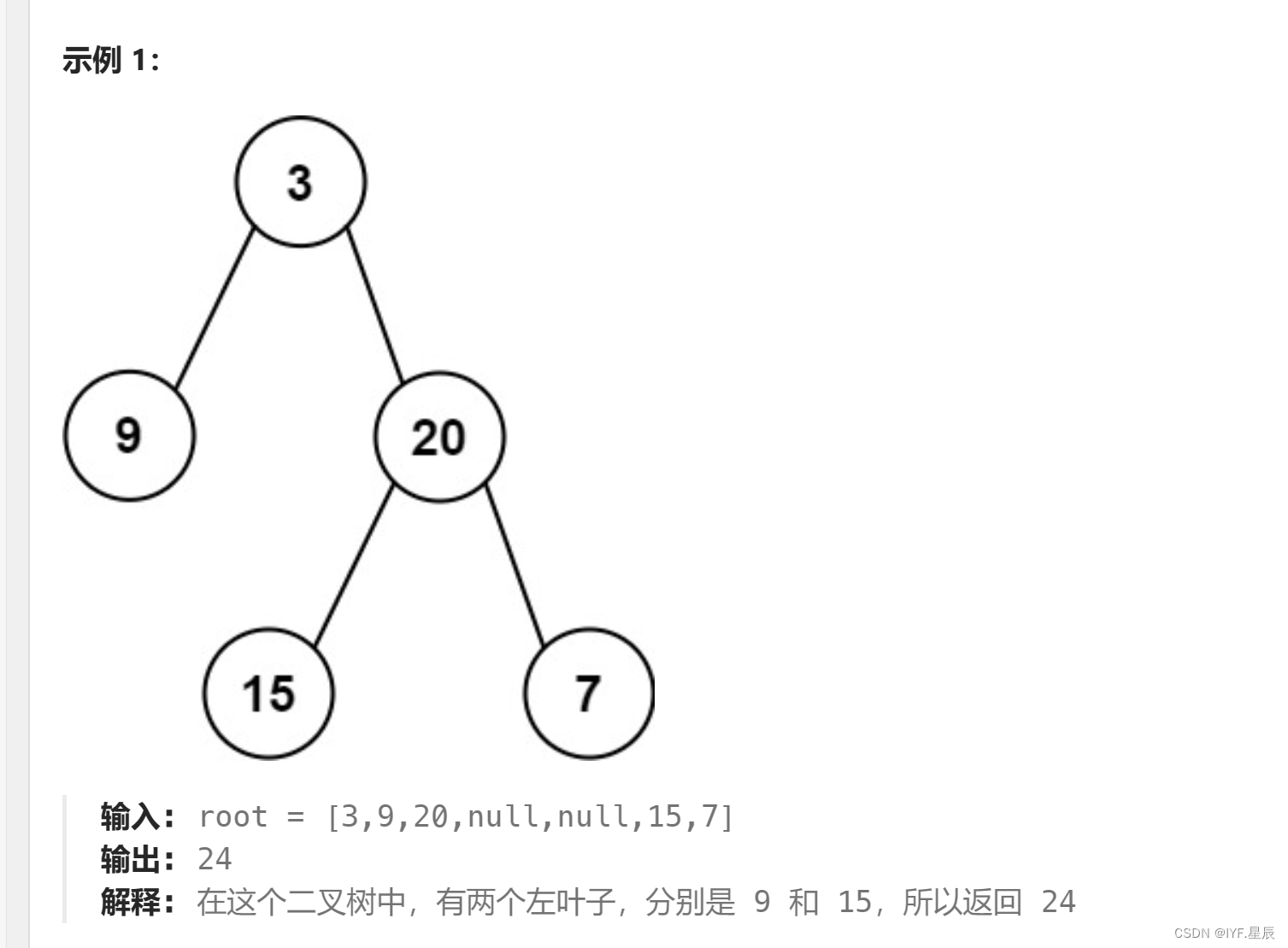
题目链接:404. 左叶子之和 - 力扣(LeetCode)
题解:通过给函数传一个boolean值通过二叉树的遍历来判断是否是左叶子节点。然后将是左叶子节点的值相加
class Solution {int res = 0;public void dfs(TreeNode root,boolean isLeft){if(root == null){return ;}//判断是否是左叶子节点,是就加上if(root.left == null && root.right == null && isLeft){res += root.val;}dfs(root.left,true);dfs(root.right,false);}public int sumOfLeftLeaves(TreeNode root) {dfs(root,false);return res;}
}例7:翻转二叉树:
题目:
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
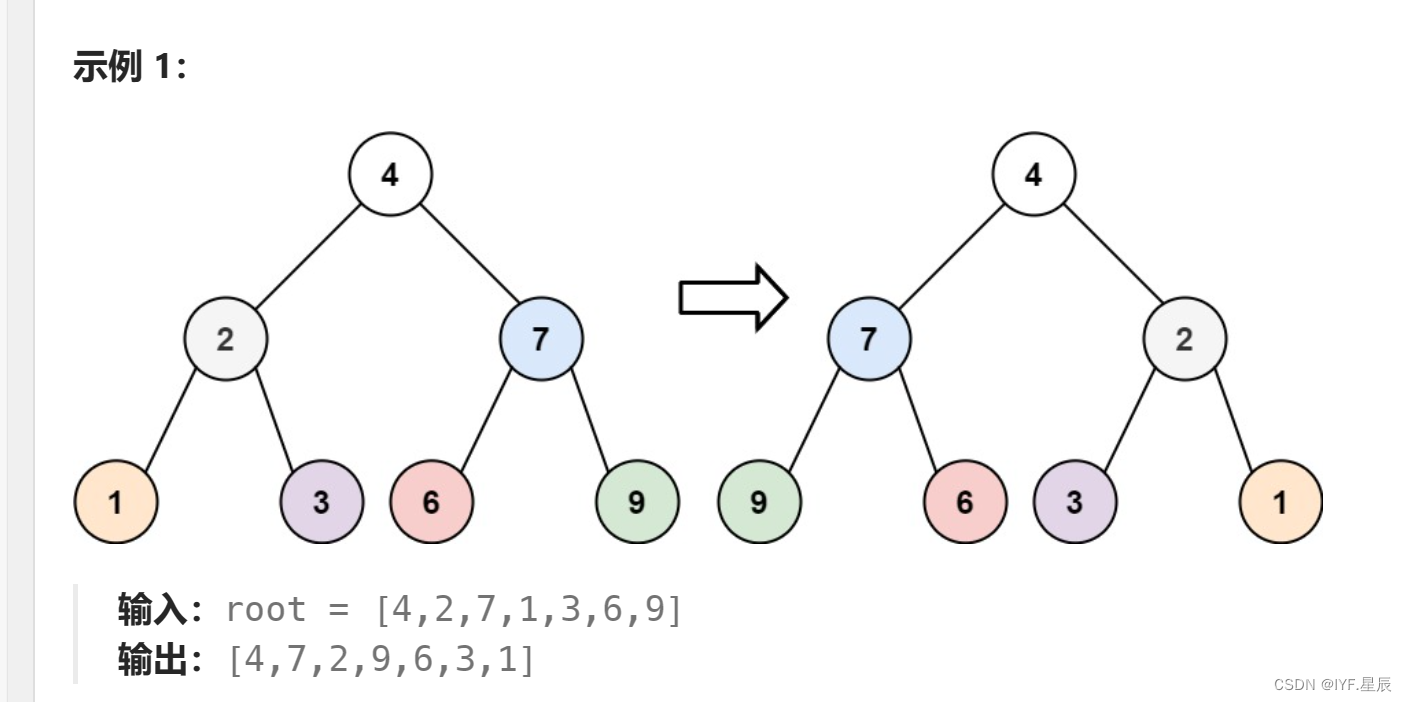
题目链接:226. 翻转二叉树 - 力扣(LeetCode)
题解:在前序遍历的基础上交换左右子树即可(图解):
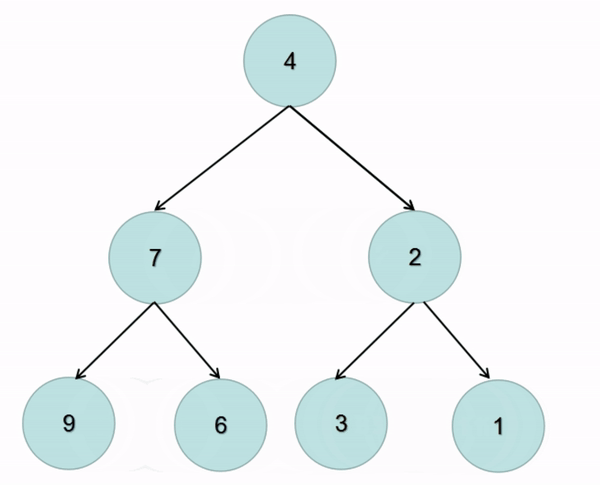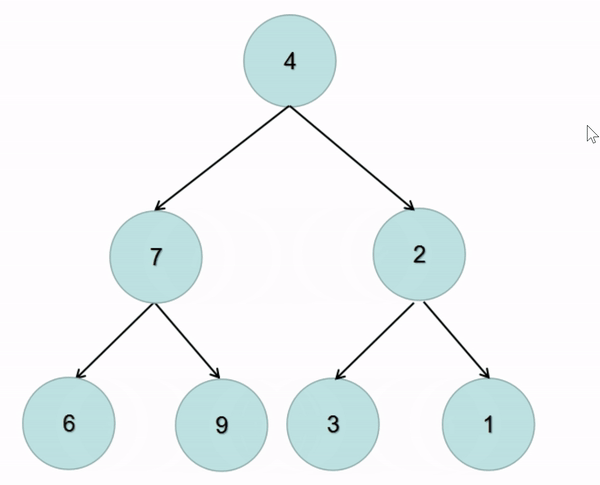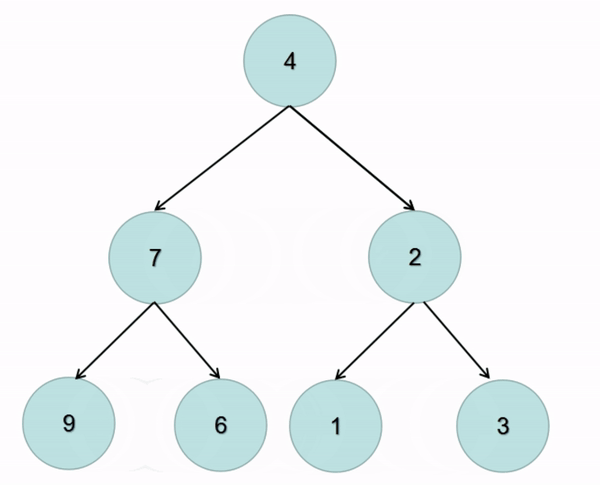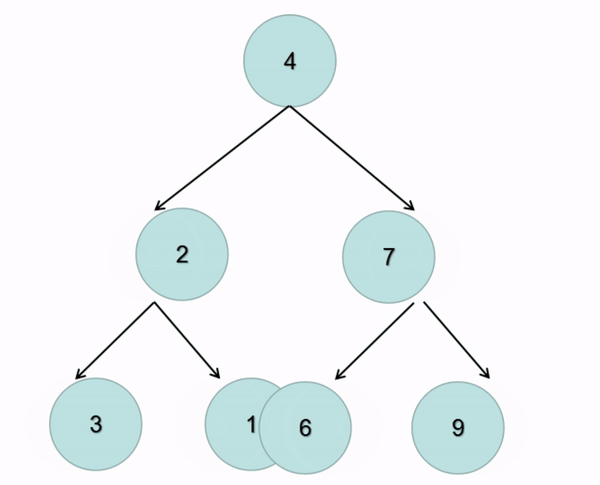
class Solution {public TreeNode invertTree(TreeNode root) {if(root == null){return null;}//交换左右子树TreeNode temp = root.left;root.left = root.right;root.right = temp;invertTree(root.left);invertTree(root.right);return root;}
}例8: 路径总和:
题目:给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
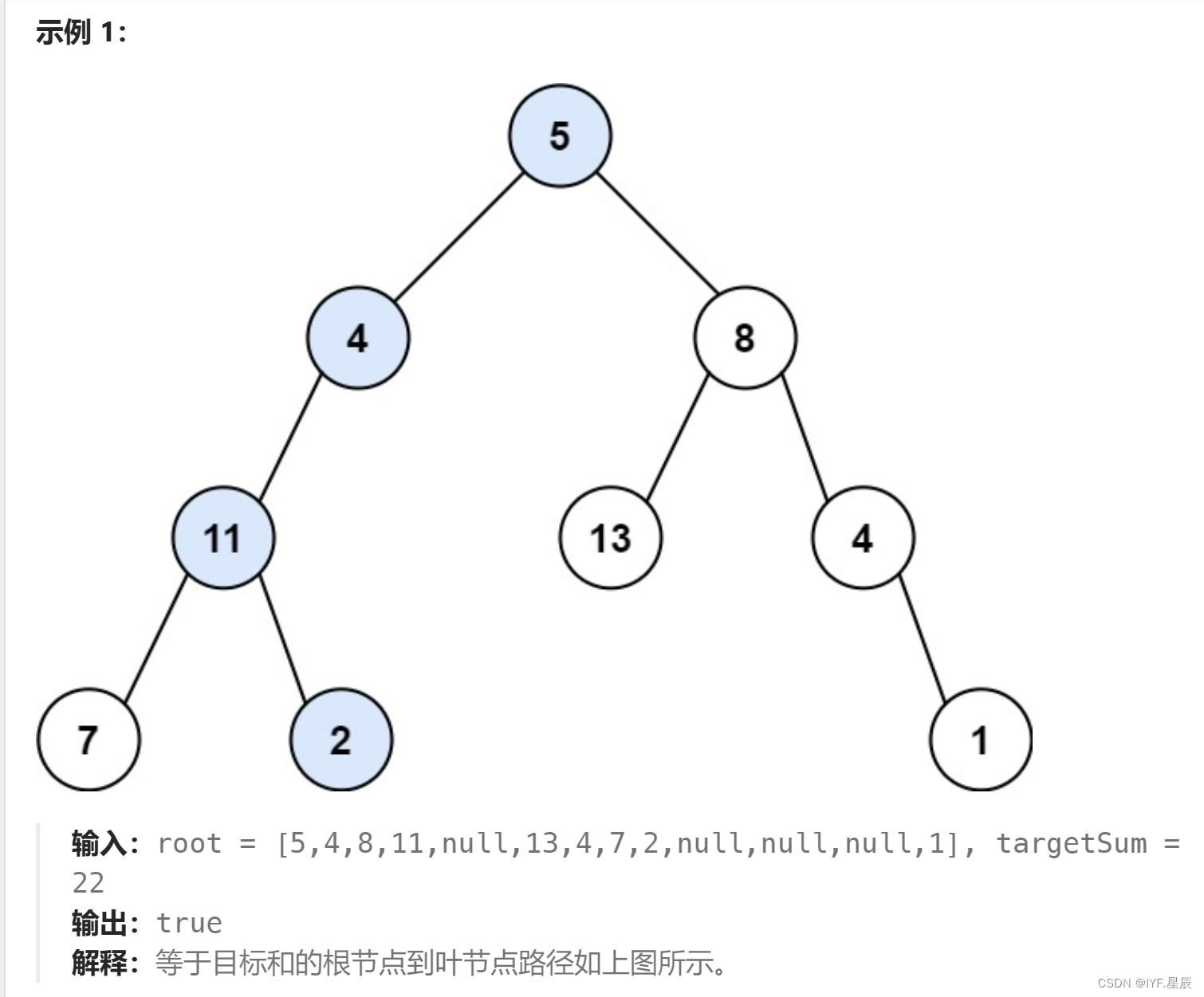
题目链接:112. 路径总和 - 力扣(LeetCode)
题解:法一:在前序遍历位置记录路径的和(节点的val值累加),后序遍历的位置删除路径的和(节点的val值减少):
class Solution {boolean found = false;int curSum = 0;int target;public void traverse(TreeNode root){if(root == null){return ;}//前序遍历不断加入节点的和curSum += root.val;//判断是否是叶子节点,是就和target值比较if(root.left == null && root.right == null){if(curSum == target){found = true;}}traverse(root.left);traverse(root.right);//后序遍历删除节点的值curSum -= root.val;}public boolean hasPathSum(TreeNode root, int targetSum) {if(root == null){return false;}this.target = targetSum;traverse(root);return found;}
}法二:将路径和不断分解为子树的路径和:
lass Solution {/* 解法一、分解问题的思路 */// 定义:输入一个根节点,返回该根节点到叶子节点是否存在一条和为 targetSum 的路径public boolean hasPathSum(TreeNode root, int targetSum) {// base caseif (root == null) {return false;}// root.left == root.right 等同于 root.left == null && root.right == nullif (root.left == root.right && root.val == targetSum) {return true;}return hasPathSum(root.left, targetSum - root.val)|| hasPathSum(root.right, targetSum - root.val);}
例9:路径总和II:
题目:
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
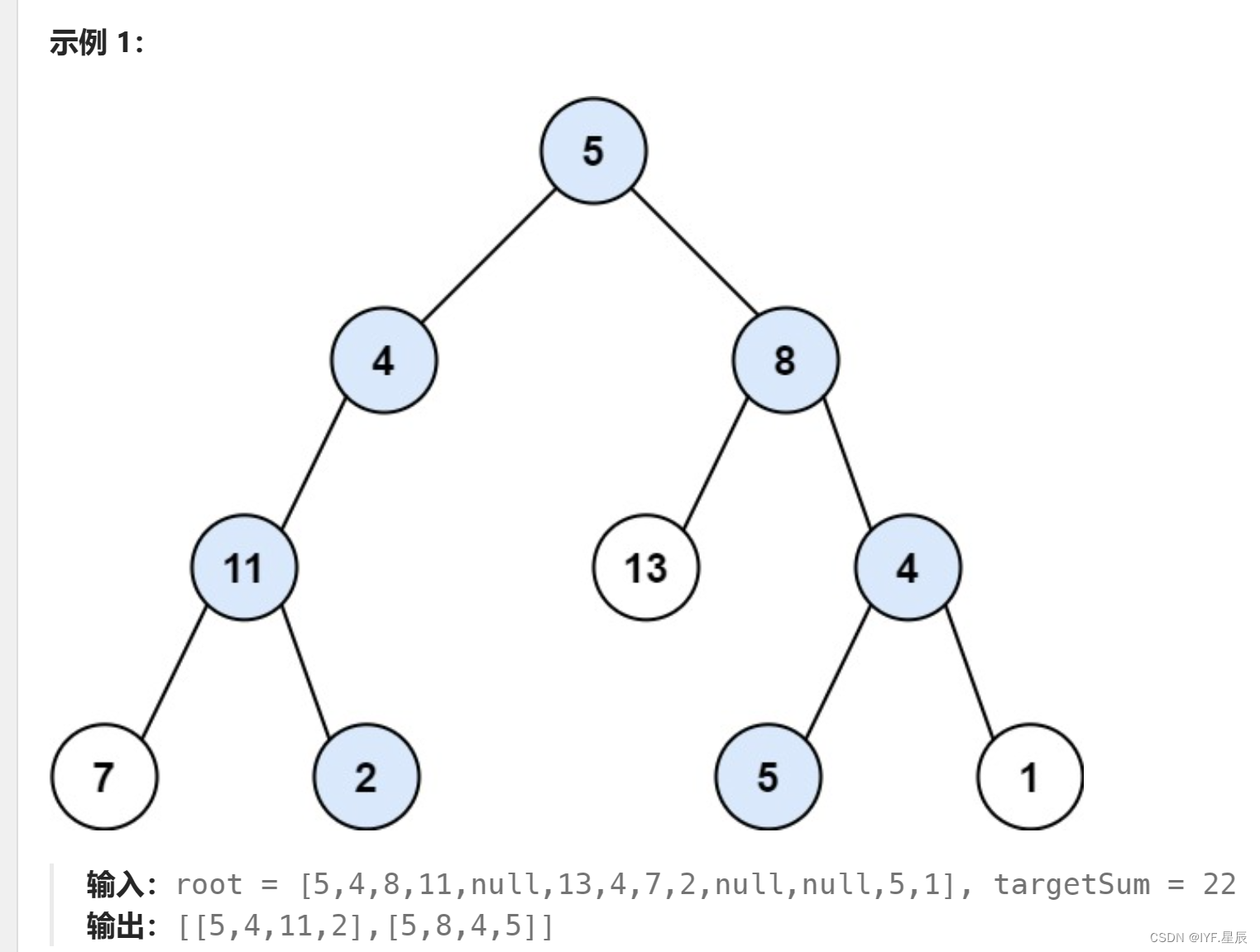
题目链接:113. 路径总和 II - 力扣(LeetCode)
题解:遍历一遍二叉树,就可以把所有符合条件的路径找出来。为了维护经过的路径,在进入递归的时候要在 path 列表添加节点,结束递归的时候删除节点。
class Solution {List<List<Integer>> res = new LinkedList<>();public List<List<Integer>> pathSum(TreeNode root, int sum) {if (root == null) return res;traverse(root, sum, new LinkedList<>());return res;}// 遍历二叉树private void traverse(TreeNode root, int sum, LinkedList<Integer> path) {if (root == null) return;int remain = sum - root.val;if (root.left == null && root.right == null) {if (remain == 0) {// 找到一条路径path.addLast(root.val);res.add(new LinkedList<>(path));path.removeLast();}return;}// 维护路径列表path.addLast(root.val);traverse(root.left, remain, path);path.removeLast();path.addLast(root.val);traverse(root.right, remain, path);path.removeLast();}
}例10:二叉树展开为链表:
题目:
给你二叉树的根结点 root ,请你将它展开为一个单链表:
- 展开后的单链表应该同样使用
TreeNode,其中right子指针指向链表中下一个结点,而左子指针始终为null。 - 展开后的单链表应该与二叉树 先序遍历 顺序相同。
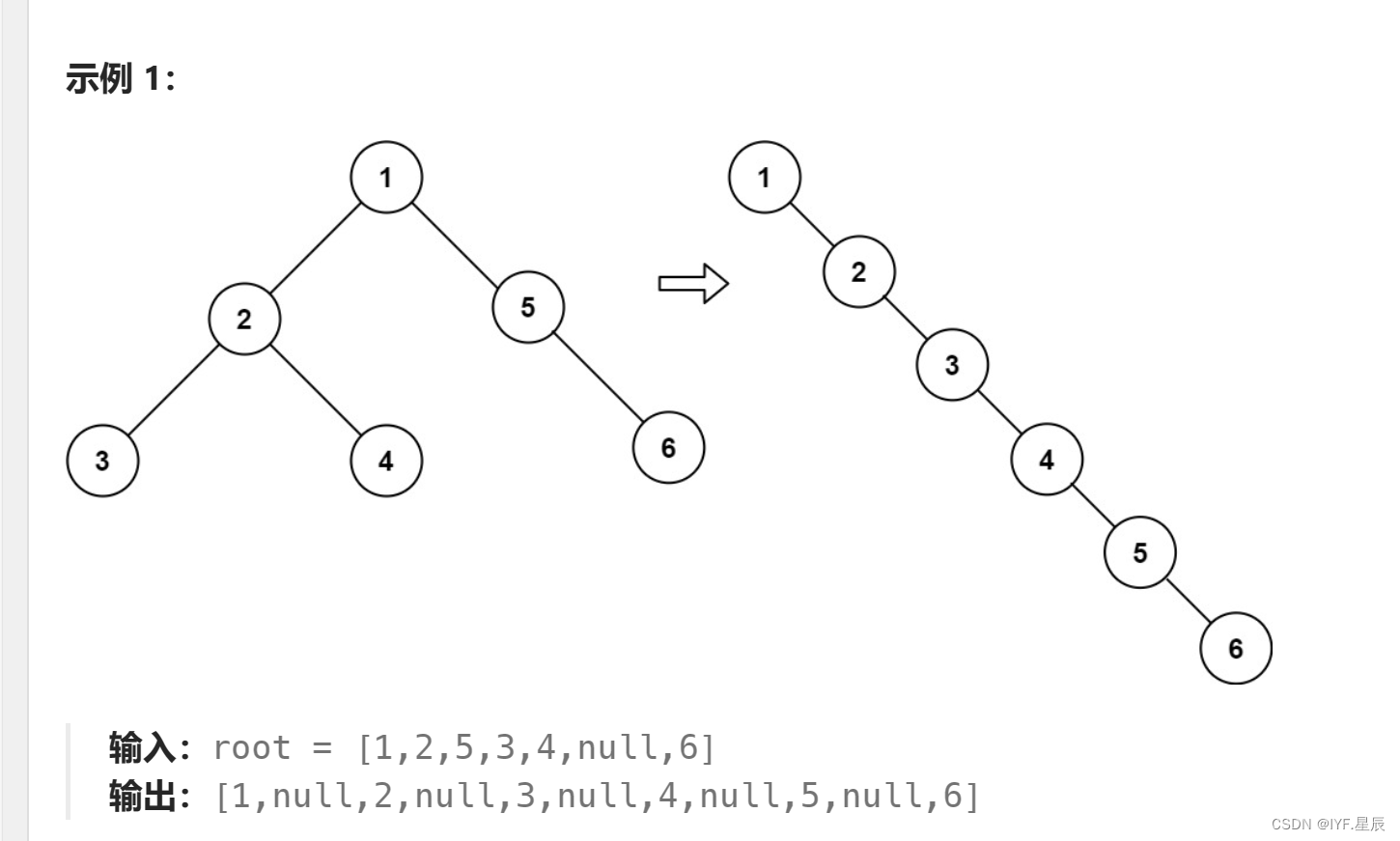
题目链接:114. 二叉树展开为链表 - 力扣(LeetCode)
题解:只要运用二叉树的递归遍历框架即可;后者的关键在于明确递归函数的定义,然后利用这个定义,这题就属于后者,flatten 函数的定义如下:给 flatten 函数输入一个节点 root,那么以 root 为根的二叉树就会被拉平为一条链表。流程:
1、将 root 的左子树和右子树拉平。
2、将 root 的右子树接到左子树下方,然后将整个左子树作为右子树。
class Solution {// 定义:将以 root 为根的树拉平为链表public void flatten(TreeNode root) {// base caseif (root == null) return;// 先递归拉平左右子树flatten(root.left);flatten(root.right);/****后序遍历位置****/// 1、左右子树已经被拉平成一条链表TreeNode left = root.left;TreeNode right = root.right;// 2、将左子树作为右子树root.left = null;root.right = left;// 3、将原先的右子树接到当前右子树的末端TreeNode p = root;while (p.right != null) {p = p.right;}p.right = right;}
}
结语: 写博客不仅仅是为了分享学习经历,同时这也有利于我巩固自己的知识点,总结该知识点,由于作者水平有限,对文章有任何问题的还请指出,接受大家的批评,让我改进。同时也希望读者们不吝啬你们的点赞+关注+收藏,你们的鼓励是我创作的最大动力!

相关文章:

通过二叉树例题深入理解递归问题
目录 引入: 例1:二叉树的前序遍历: 例2: N叉树的前序遍历: 例3:二叉树的最大深度: 例4:二叉树的最小深度 例5:N叉树的最大深度: 例6:左叶子…...

【Android 协程常见用法】
我们这里只讲解一下,协程在Android项目中常见用法,原理知识不在进行说明了。 依赖 lifecycleScope只能在Activity、Fragment中使用,会绑定Activity和Fragment的生命周期。依赖库: implementation androidx.lifecycle:lifecycle…...
python 进程笔记一 (概念+示例代码)
1. 进程的概念 进程是资源分配的最小单位,也是线程的容器,线程(python 线程 (概念示例代码))是CPU调度的基本单位,一个进程包括多个线程。 程序:例如xxx.py是一个程序 进程…...

各中间件数据库默认访问端口总结
说明 在生态丰富的开发环境下,我们常常需要接触很多中间件产品,中间件默认的连接端口以及可视化ui访问端口也时不时的需要用到,这里循序渐进做好登记,以备查阅! 中间件/数据库名称默认端口管理台端口默认账号密码rabbi…...

鲲鹏arm64架构下安装KubeSphere
鲲鹏arm64架构下安装KubeSphere 官方参考文档: https://kubesphere.io/zh/docs/quick-start/minimal-kubesphere-on-k8s/ 在Kubernetes基础上最小化安装 KubeSphere 前提条件 官方参考文档: https://kubesphere.io/zh/docs/installing-on-kubernetes/introduction/prerequi…...

python 函数-02-返回值注释格式
01 函数返回值 1)python中函数可以没有返回值,也可以有通过return的方式 – 【特殊性,区别于java c#等】 2)返回值可以是一个或者多个,多个时通过逗号隔开 – 【特殊性,区别于java c#等】 3)多…...
【前端素材】推荐优质后台管理系统Upcube平台模板(附源码)
一、需求分析 后台管理系统在多个层次上提供了丰富的功能和细致的管理手段,帮助管理员轻松管理和控制系统的各个方面。其灵活性和可扩展性使得后台管理系统成为各种网站、应用程序和系统不可或缺的管理工具。 当我们从多个层次来详细分析后台管理系统时࿰…...
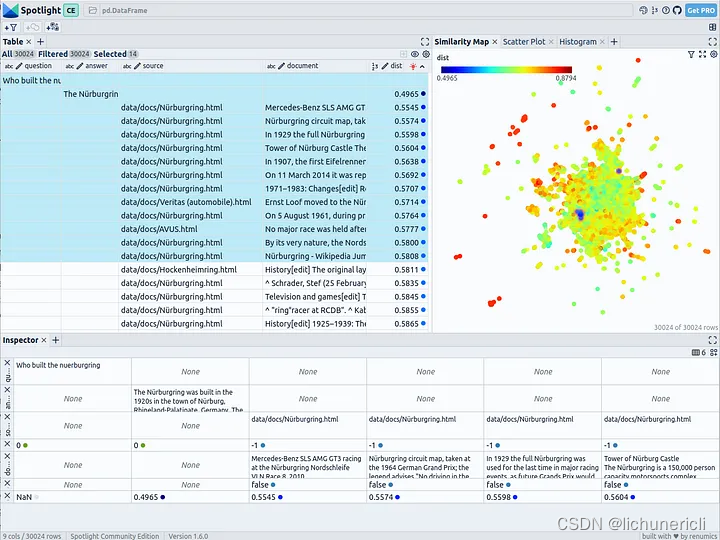
可视化 RAG 数据 — 用于检索增强生成的 EDA
原文地址:Visualize your RAG Data — EDA for Retrieval-Augmented Generation 2024 年 2 月 8 日 Github:https://github.com/Renumics/rag-demo/blob/main/notebooks/visualize_rag_tutorial.ipynb 为探索Spotlight中的数据,我们使用Pa…...

数学建模论文、代码百度网盘链接
1.[2018中国大数据年终总决赛冠军] 金融市场板块划分与轮动规律挖掘与可视化问题 2.[2019第九届MathorCup数模二等奖] 数据驱动的城市轨道交通网络优化策略 3.[2019电工杯一等奖] 露天停车场停车位的优化设计 4.[2019数学中国网络数模一等奖] 基于机器学习的保险业数字化变革…...

mysql 迁移-data目录拷贝方式
背景:从服务器进水坏掉,50多G的数据库要重新做主从,但以导入导出的方式太慢,简直是灾难性的,一夜都没好,只好想到了拷贝mysql数据文件的方式 拷贝的数据文件的前提 1.数据库版本必需一致(可以…...
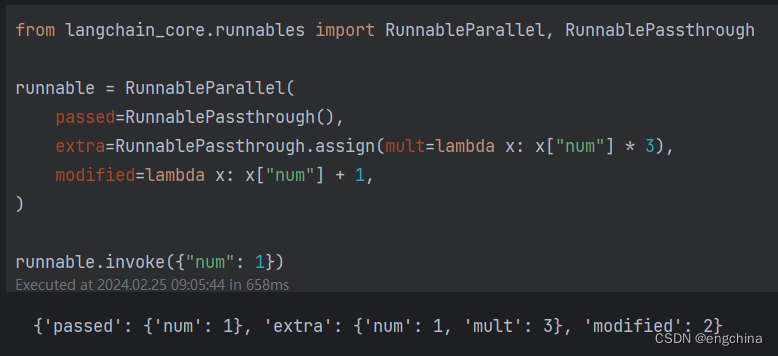
学习 LangChain 的 Passing data through
学习 LangChain 的 Passing data through 1. Passing data through2. 示例 1. Passing data through RunnablePassthrough 允许不改变或添加额外的键来传递输入。这通常与 RunnableParallel 结合使用,将数据分配给映射中的新键。 RunnablePassthrough() 单独调用&…...
C# OpenVINO PaddleSeg实时人像抠图PP-MattingV2
目录 效果 项目 代码 下载 C# OpenVINO 百度PaddleSeg实时人像抠图PP-MattingV2 效果 项目 代码 using OpenCvSharp; using Sdcb.OpenVINO; using System; using System.Diagnostics; using System.Drawing; using System.Security.Cryptography; using System.Text; us…...

【Android 11】AOSP Settings WIFI随机MAC地址功能
AOSP Settings WIFI随机MAC地址功能 背景 最近客户提出了想要实现随机WIFIMAC地址的功能(我们默认WIFI的MAC地址是固定的)。网上搜到了一篇不错的文章,本次改动也是基于这个来写的。 由于客户指定使用的settings是AOSP的,所以在…...

dmrman备份还原
脱机还原工具-dmrman 前言 根据达梦官网文档整理 一、概述 DMRMAN 命令行设置参数执行又可分为命令行指定脚本、命令行指定语句两种执行方式。 指定语句 $ DMRMAN RMAN>BACKUP DATABASE/dmdata/data/DAMENG/dm.ini;指定脚本 创建一个名为 cmd_file.txt 的文件&#x…...

网页403错误(Spring Security报异常 Encoded password does not look like BCrypt)
这个错误通常表现为"403 Forbidden"或"HTTP Status 403",它指的是访问资源被服务器理解但拒绝授权。换句话说,服务器可以理解你请求看到的页面,但它拒绝给你权限。 也就是说很可能测试给定的参数有问题,后端…...
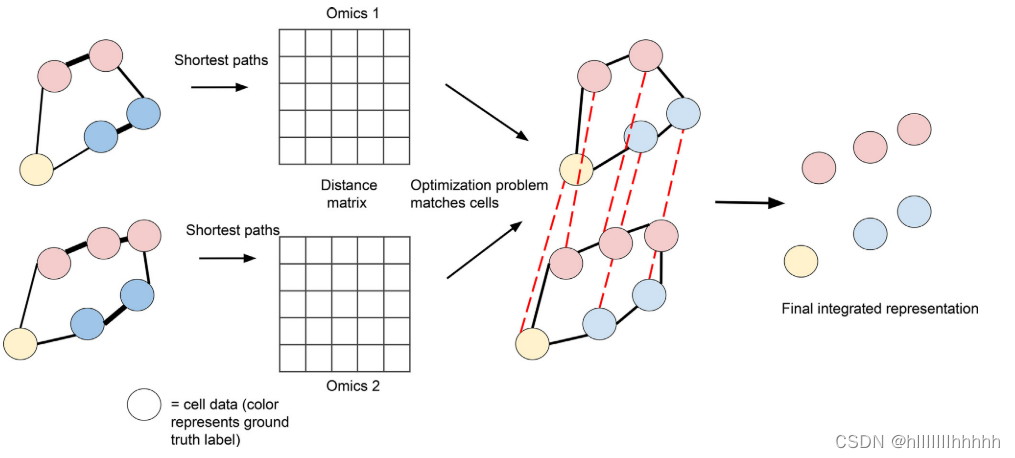
单细胞多组学整合与对齐的计算方法
Computational Methods for Single-cell Multi-omics Integration and Alignment Bioinformatics-2022-密西根大学 关键词:单细胞;多组学;机器学习;无监督学习;集成 摘要 最近发展起来的生成单细胞基因组数据的技术在生物学领域产生了革命性的影响。多组学测定提…...

33.openeuler OECA认证模拟题16
一 、选择题 1.如何查看系统支持的 shell? A、cat /etc/passwd B、cat /etc/shells C、echo SSHELL D、echo $0 答案 :B 2.下列哪项不是 shell的功能? A 、 用户界面,提供用户与内核交互接口 B 、 命令解释器 C 、提供编译环境 D 、 提供各种管理工具,…...

javaScript数组去重的几种实现方式——适用非引用数据去重
最传统的使用循环遍历 //最传统的使用循环遍历 function getUnique(arr) {let newArr [];for (let i 0; i < arr.length; i) {for (let j i 1; j < arr.length; j) {if (arr[i] arr[j]) {i; //相同丢掉前面的元素}}newArr.push(arr[i]);}return newArr; } 利用Set实…...
Nexus Repository Manager
Nexus Repository Manager https://s01.oss.sonatype.org/#welcome https://mvnrepository.com/-CSDN博客...

Python世界之运算符
一、算术运算符 以下假设变量: a10,b20: 运算符 描述 实例 加 - 两个对象相加 a b 输出结果 30 - 减 - 得到负数或是一个数减去另一个数 a - b 输出结果 -10 * 乘 - 两个数相乘或是返回一个被重复若干次的字符串 a * b 输出结…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

小智AI+MCP
什么是小智AI和MCP 如果还不清楚的先看往期文章 手搓小智AI聊天机器人 MCP 深度解析:AI 的USB接口 如何使用小智MCP 1.刷支持mcp的小智固件 2.下载官方MCP的示例代码 Github:https://github.com/78/mcp-calculator 安这个步骤执行 其中MCP_ENDPOI…...
