仪表放大器放大倍数分析-运算放大器
仪表放大器是一种非常特殊的精密差分电压放大器,它的主要特点是采用差分输入、具有很高的输入阻抗和共模抑制比,能够有效放大在共模电压干扰下的信号。本文简单分析一下三运放仪表放大器的放大倍数。
一、放大倍数理论分析
三运放仪表放大器的电路结构如下图所示,可以将整个电路分为两级:第一级为两个同相比例运算电路,第二级为差分运算电路。
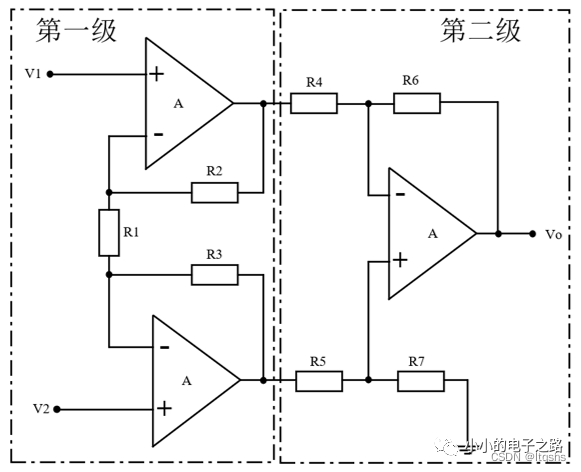
1、第一级电路分析
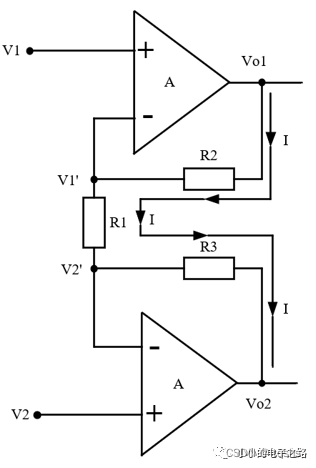
根据运放的虚短可以得到:
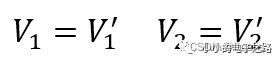
同时根据虚断可以得到流经电阻R1、R2、R3的电流近似相等,记为I。
易知
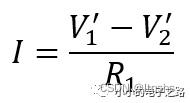
此时可以得到
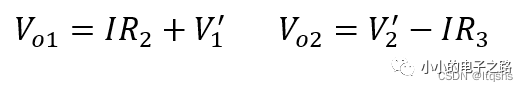
因此,第一级电路的电压放大倍数
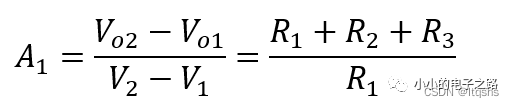
值得注意的是,该放大倍数为差模电压放大倍数。
当输入信号为共模信号时,
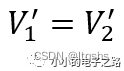
因此,流经电阻R3的电流
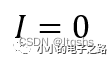
此时两个运放相当于两个电压跟随器,因此其共模增益为1。
根据上述分析可以得到:
(1)输入端的两个同相比例运算电路可以提高整个电路的输入阻抗;
(2)差模增益可调,共模增益始终为1,提高差模增益可以提高共模抑制比。
2、第二级电路分析
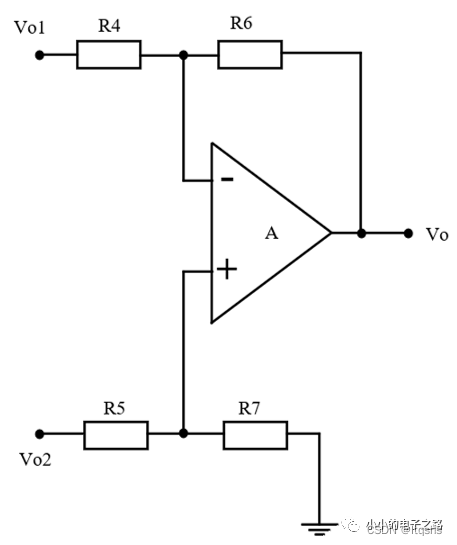
假设R4=R5、R6=R7,此时根据差分放大电路的放大倍数计算公式可以得到第二级电路的差模放大倍数
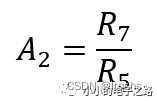
因此该仪表放大器的差模放大倍数
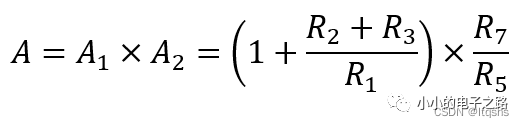
二、仿真分析
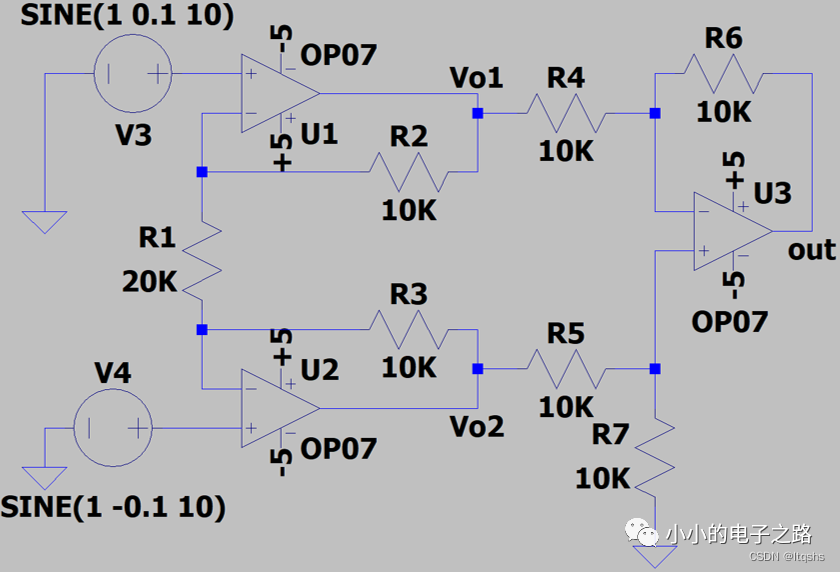
令电阻R1=20kΩ,R2=R3=R4=R5=R6=R7=10 kΩ,在电路的两端输入频率为10Hz,直流分量为1V,峰峰值为200mV,相位相差180°的两路正弦信号。根据上述理论分析可得,第一级电路的差模放大倍数为2,共模放大倍数为1;整个电路的放大倍数为2。
1、观察第一级电路的输入与输出波形,即(V2-V1)与(Vo2-Vo1)的波形,可以看出,第一级电路的放大倍数近似为2,符合上述理论计算。
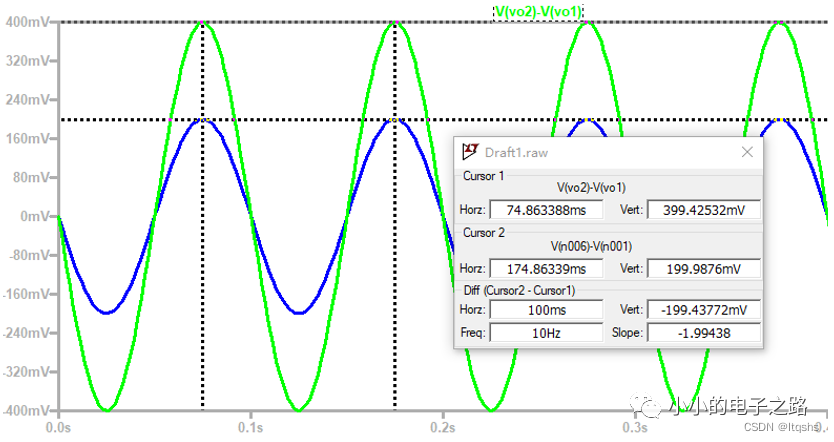
2、观察第一级电路的单端输入输出波形,即V1与Vo1的波形,可以看出,输入共模信号为1V,输出共模信号仍为1V,共模增益为1,与理论分析相符。
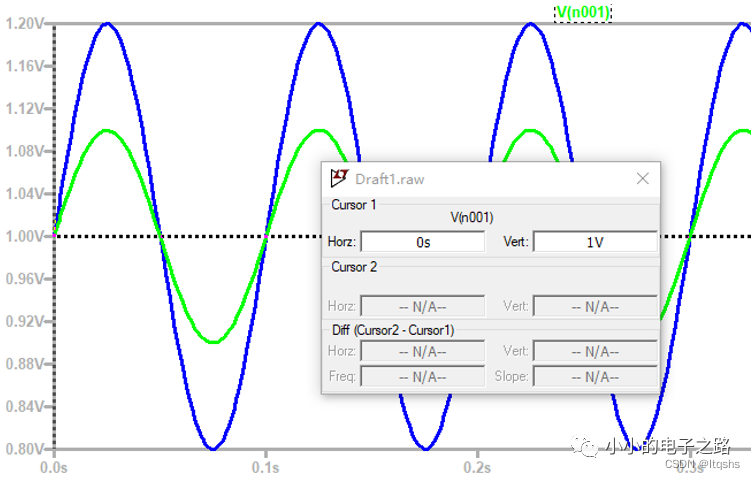
3、观察整个电路的传递函数,可以看出,整个电路的放大倍数近似为2,符合理论计算,同时根据仿真结果也可以看出,仪表放大器具有很大的输入阻抗,其输出阻抗则很小。

参考原文:《仪表放大器放大倍数分析》
相关文章:

仪表放大器放大倍数分析-运算放大器
仪表放大器是一种非常特殊的精密差分电压放大器,它的主要特点是采用差分输入、具有很高的输入阻抗和共模抑制比,能够有效放大在共模电压干扰下的信号。本文简单分析一下三运放仪表放大器的放大倍数。 一、放大倍数理论分析 三运放仪表放大器的电路结构…...
laravel8多模块、多应用和多应用路由
1、安装多应用模块 composer require nwidart/laravel-modules2、执行命令,config文件夹下生成一个modules.php配置文件 php artisan vendor:publish --provider"Nwidart\Modules\LaravelModulesServiceProvider"3、修改config文件夹下的modules.php&am…...

【Java学习笔记】6.Java 变量类型
Java 变量类型 在Java语言中,所有的变量在使用前必须声明。声明变量的基本格式如下: type identifier [ value][, identifier [ value] ...] ;格式说明:type为Java数据类型。identifier是变量名。可以使用逗号隔开来声明多个同类型变量。 …...

Promise对象状态属性 工作流程 Promise对象的几个属性
Promise 对象状态属性介绍 实例对象中的一个属性 PromiseState pending 1、pending 变为 resolved / fullfilled 成功 2、pending 变为 rejected 失败 说明:只有这2种,且一个promise对象只能改变一次 无论变为成功还是失败,都会有一个结果…...

webgpu思考obj携带属性
今天在搞dbbh.js的时候,想到一个问题,啥问题呢,先看看情况 画2个材质不相同的box的时候 首先开始createCommandEncoder,然后beginRenderPass,分歧就在这里了 第一个box,他有自己的pipeline,第二个也有,那么…...
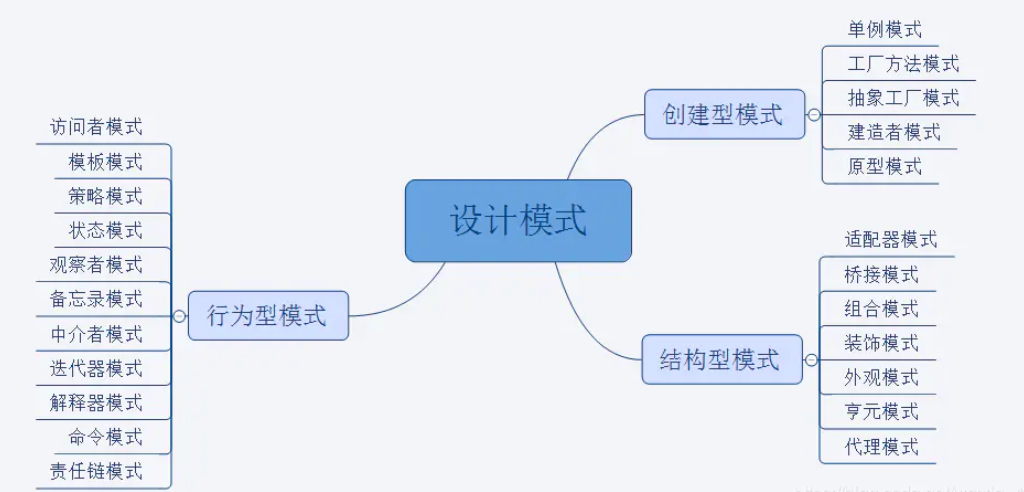
设计模式(只谈理解,没有代码)
1.什么是设计模式设计模式,是一套被反复使用、多数人知晓的、经过分类编目的、代码设计经验的总结。使用设计模式是为了可重用代码、让代码更容易被他人理解、保证代码可靠性、程序的重用性。2.为什么要学习设计模式看懂源代码:如果你不懂设计模式去看Jd…...

06、Eclipse 中使用 SVN
Eclipse 中使用 SVN1 在 Eclipse 中安装 SVN 客户端插件1.1 在线安装1.2 离线安装2 SVN 在 Eclipse 分享3 检出提交更新3.1 检出3.2 提交3.3 更新4 Eclipse 中 SVN 图标及其含义4.1 ?图标4.2 图标4.3 金色圆柱图标4.4 * 图标5 恢复历史版本5.1 恢复步骤5.2 权限控制…...

Zookeeper3.5.7版本——客户端命令行操作(命令行语法)
目录一、命令行语法二、help命令行语法示例一、命令行语法 命令行语法列表 命令基本语法功能描述help显示所有操作命令ls path使用 ls 命令来查看当前 znode 的子节点 [可监听]-w 监听子节点变化-s 附加次级信息create普通创建-s 含有序列-e 临时(重启或者超时消失…...

2023.03.05 学习周报
文章目录摘要文献阅读1.题目2.摘要3.介绍4.SAMPLING THE OUTPUT5.LOSS FUNCTION DESIGN5.1 ranking loss: Top1 & BPR5.2 VANISHING GRADIENTS5.3 ranking-max loss fuction5.4 BPR-max with score regularization6.实验7.结论深度学习1.相关性1.1 什么是相关性1.2 协方差1…...
java Spring JdbcTemplate配合mysql实现数据批量修改
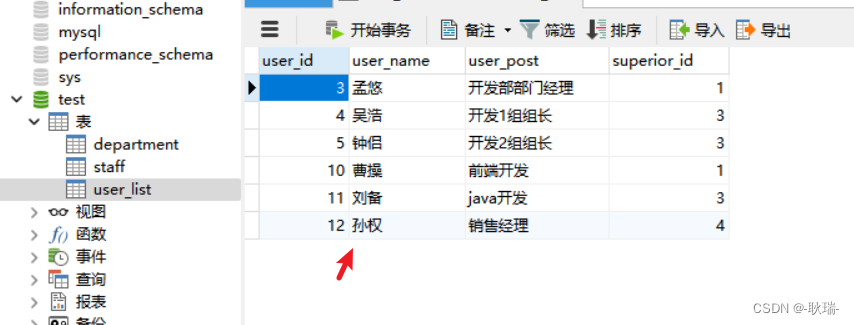
其实这个操作和批量添加挺像的 调的同一个方法 首先 我们看数据库结构 这是我本地的 mysql 里面有一个test数据库 里面有一张user_list表 然后创建一个java项目 然后 引入对应的JAR包 在src下创建 dao 目录 在下面创建一个接口 叫 BookDao 参考代码如下 package dao;impo…...
《算法分析与设计》笔记总结
《算法分析与设计》笔记总结第一章 算法引论1.1 算法与程序1.2 表达算法的抽象机制1.3 描述算法1.4 算法复杂性分析第二章 递归与分治策略2.1 递归的概念2.2 分治法的基本思想2.3 二分搜索技术2.4 大整数乘法2.5 Strassen矩阵乘法2.7 合并排序2.8 快速排序2.9 线性时间选择2.10…...

序列化与反序列化概念
序列化是指将对象的状态信息转换为可以存储或传输的形式的过程。 在Java中创建的对象,只要没有被回收就可以被复用,但是,创建的这些对象都是存在于JVM的堆内存中,JVM处于运行状态时候,这些对象可以复用, 但…...
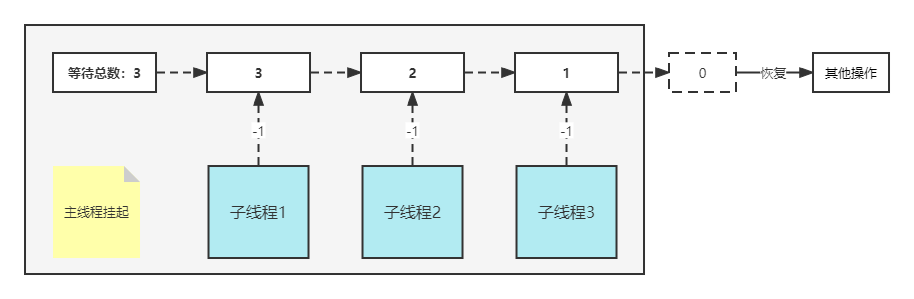
【Java并发编程】CountDownLatch
CountDownLatch是JUC提供的解决方案 CountDownLatch 可以保证一组子线程全部执行完牛后再进行主线程的执行操作。例如,主线程启动前,可能需要启动并执行若干子线程,这时就可以通过 CountDownLatch 来进行控制。 CountDownLatch是通过一个线程…...

【iOS】Blocks
BlockBlocks概要什么是Blocks?Block语法Block类型变量截获自动变量值__block说明符Blocks的实现Block的实质Blocks概要 什么是Blocks? Blocks可简单概括为: 带有自动变量(局部变量)的匿名函数 在使用Blocks时&#x…...
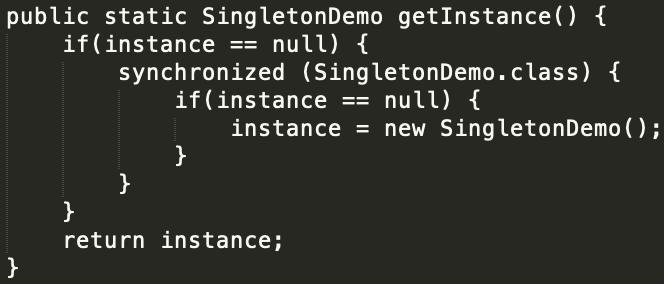
Java Volatile的三大特性
本文通过学习:周阳老师-尚硅谷Java大厂面试题第二季 总结的volatile相关的笔记volatile是Java虚拟机提供的轻量级的同步机制,三大特性为:保证可见性、不保证原子性、禁止指令重排一、保证可见性import java.util.concurrent.TimeUnit;class M…...
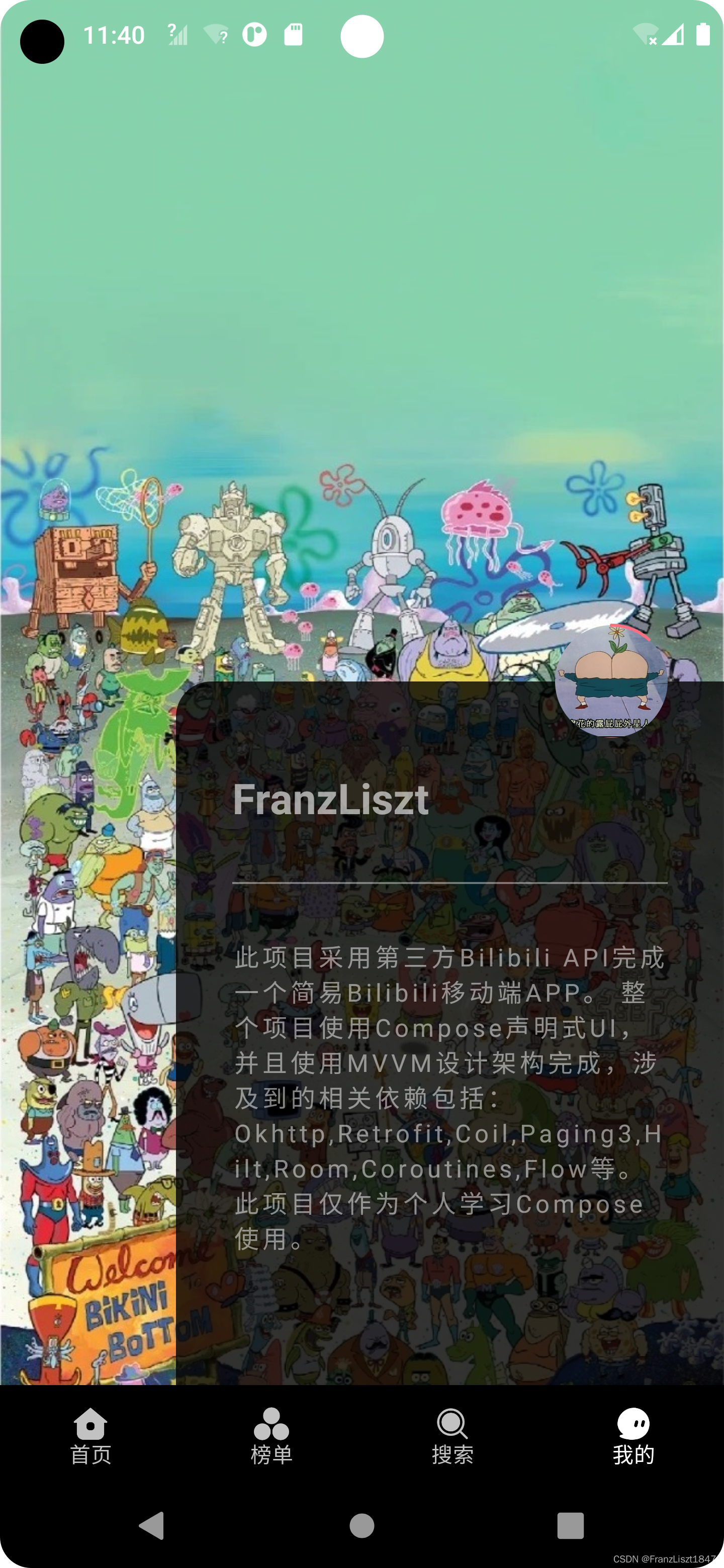
Android Compose——一个简单的Bilibili APP
Bilibili移动端APP简介依赖效果登录效果WebView自定义TobRow的Indicator大小首页推荐LazyGridView使用Paging3热门排行榜搜索模糊搜索富文本搜索结果视频详情合集信息Coroutines进行网络请求管理,避免回调地狱添加suspendwithContextGit项目链接末简介 此Demo采用A…...
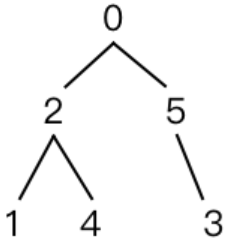
二叉树的最近公共祖先【Java实现】
题目描述 现有一棵n个结点的二叉树(结点编号为从0到n-1,根结点为0号结点),求两个指定编号结点的最近公共祖先。 注:二叉树上两个结点A、B的最近公共祖先是指:二叉树上存在的一个结点P,使得P既是…...
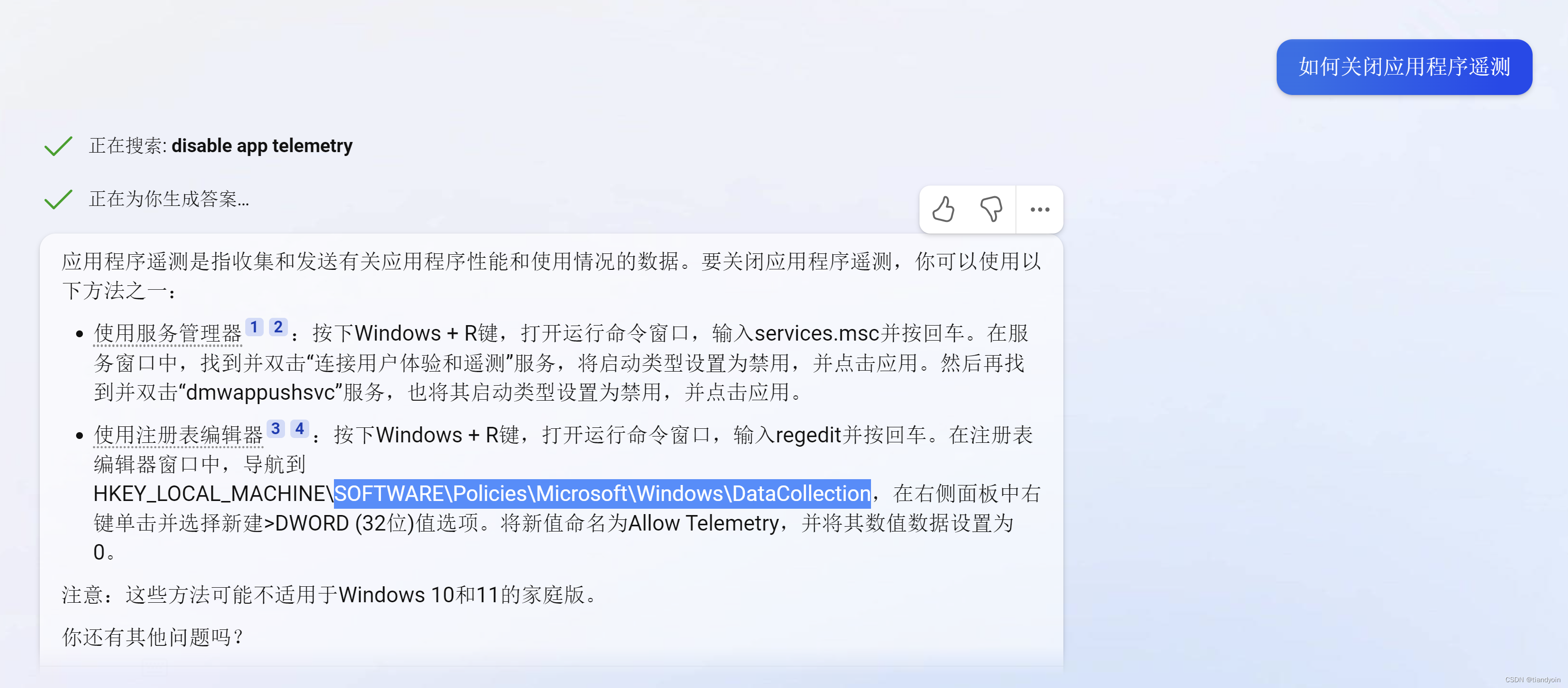
关闭应用程序遥测,禁止Windows收集用户信息
目录 1. 先创建还原点,防止意外 2. 界面设置 3. 服务 (1) GPEdit.msc - 本地计算机策略 - 计算机配置 - 管理模板 - Windows 组件 - 应用程序兼容性 - 关闭应用程序遥测 - 已启用 (2) GPEdit.msc - 本地计算机策略 - 计算机配置 - 管理模板 - Windows 组件 - 数…...

【备战面试】每日10道面试题打卡-Day4
本篇总结的是Java集合知识相关的面试题,后续也会更新其他相关内容 文章目录1、HashMap在JDK1.7和JDK1.8中有哪些不同?2、HashMap 的长度为什么是2的幂次方?3、HashMap的扩容操作是怎么实现的?4、HashMap是怎么解决哈希冲突的&…...

热乎的面经——初出茅庐
⭐️前言⭐️ 本篇文章记录博主与2023.03.04面试上海柯布西公司,一面所被问及的面试问题,回答答案仅供参考。 🍉欢迎点赞 👍 收藏 ⭐留言评论 📝私信必回哟😁 🍉博主将持续更新学习记录收获&am…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...
