动态规划 背包问题
动态规划 背包问题
问题描述:
有一个背包,总容量为12。有6件物品,每件物品的重量和价值不同,求在背包总容量12的前提下,装进物品的最大价值以及装进物品的编号
单个物品重量和价值:
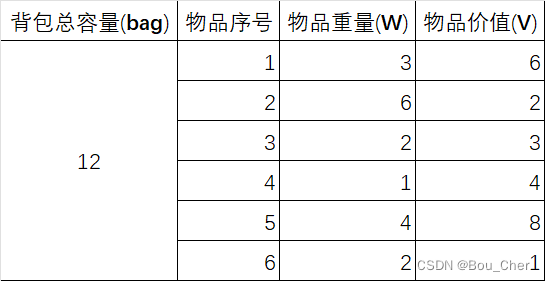
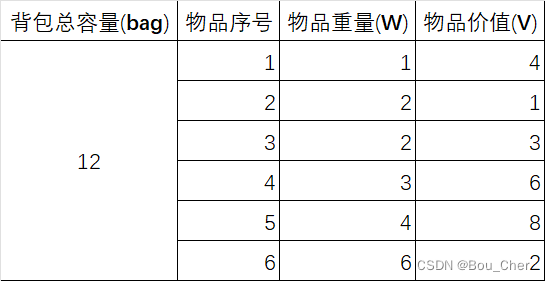
为方便进行思考,我们将物品按照重量价值递增,重新排序
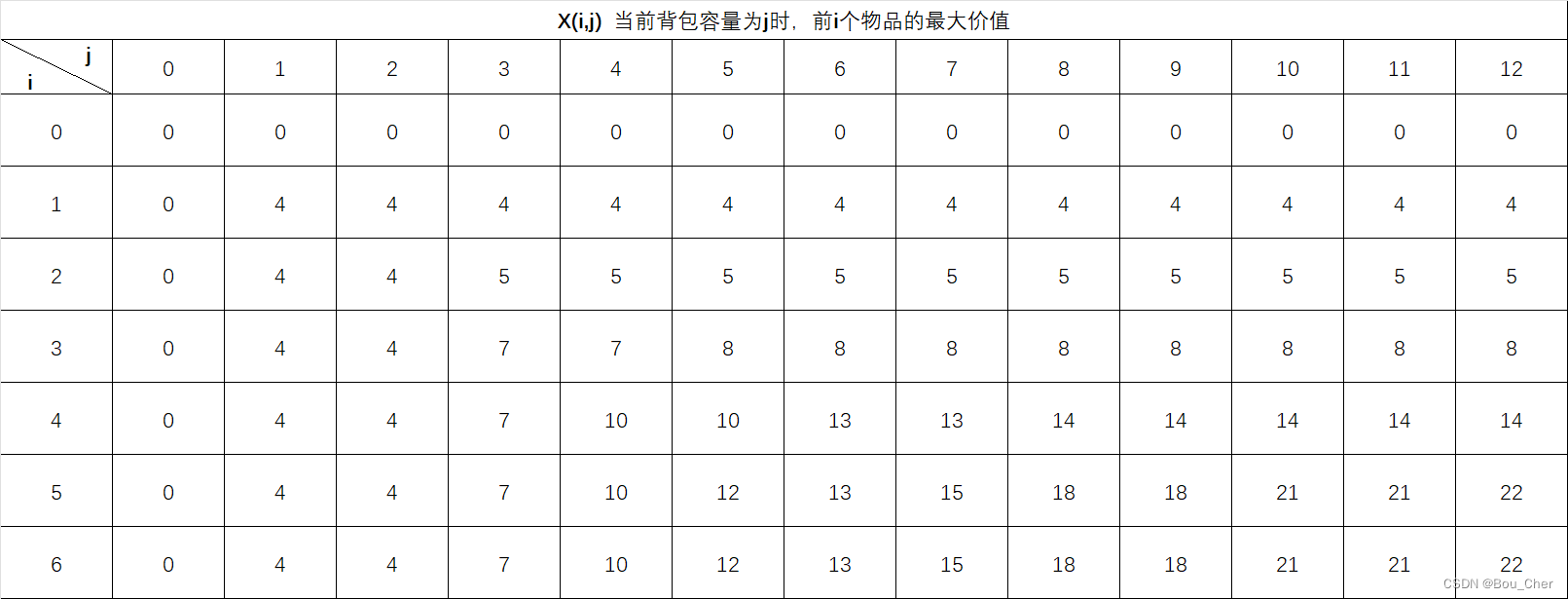
针对此问题,我们可以先列一张表格,标识当前背包容量为j时,前i个物品的最大价值。
例如X(3,3),代表当背包容量为3时,前3个物品可装入的最大价值。
第一行X(0,0)到X(0,12),代表当背包容量为0到12时,前0个物品可装入的最大价值,前0个物品不存在没有价值,即价值恒为0,因此第一行都填入0。
同理第一列X(0,0)到X(6,0),代表当背包容量为0时,第0个物品到第6个物品可装入的最大价值,因为背包容量为0,没有物品可以装下,所以第一列都填入0。
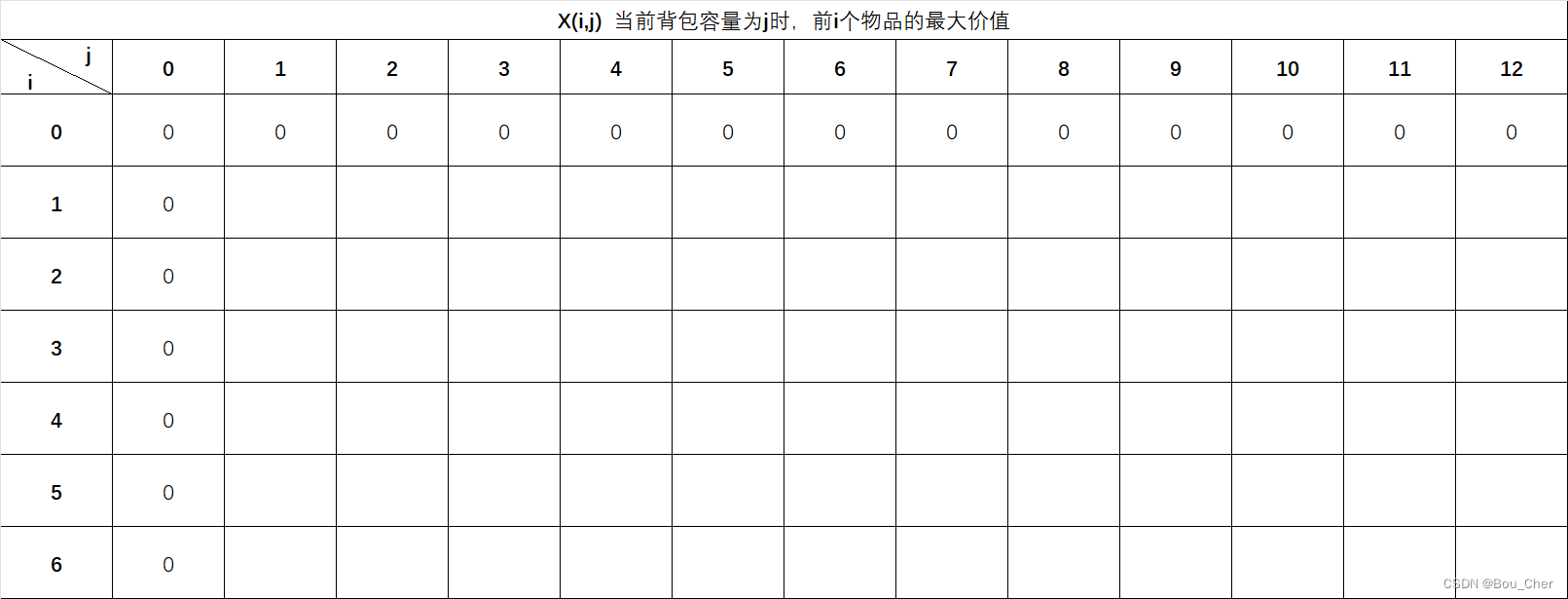
X(1,1) 代表当背包容量为1时,前1个物品的最大价值。由于W(1)=1,刚好可以装入,那么X(i,j)=X(1,1)=V(1)=4 ,因此填入4。并且不论之后背包容量如何扩展,前1个物品的最大价值恒为4。
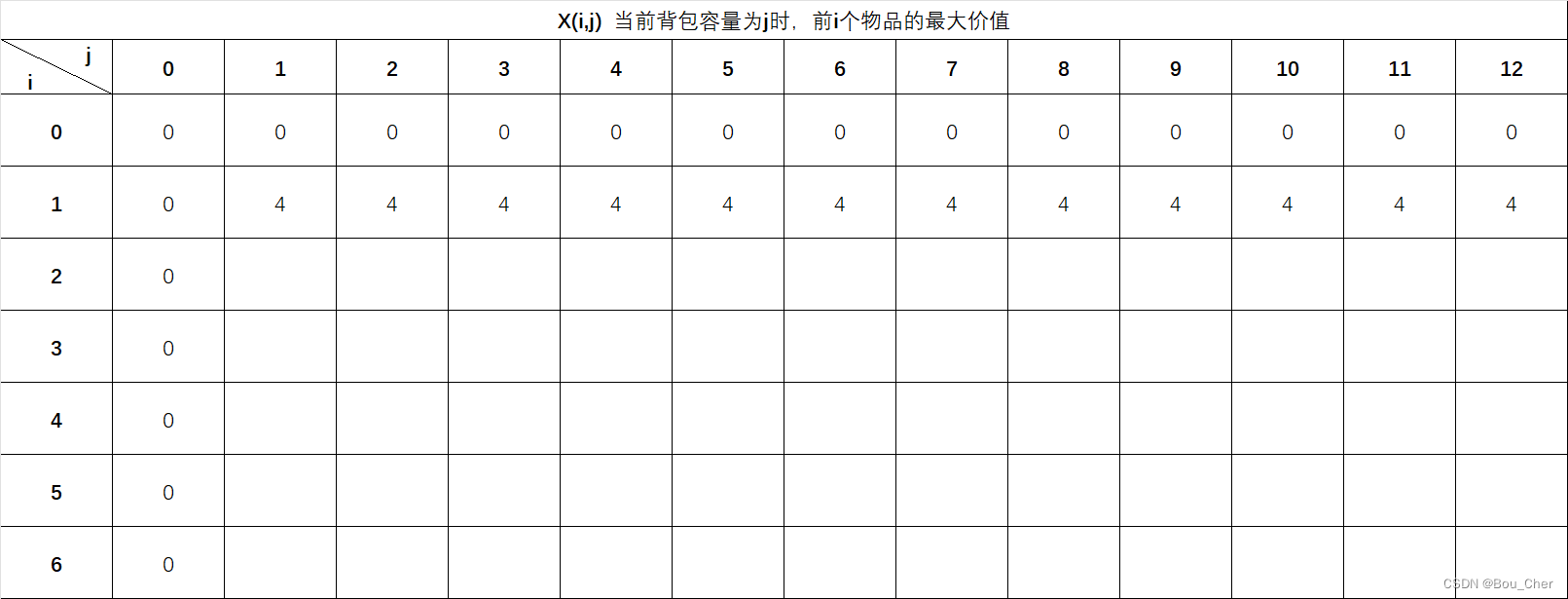
当开始第三行,即X(2,j) 填写时,就需要判断背包容量够不够装下当前物品,如果能装下,那装下当前物品和不装当前物品哪个价值最大:
-
背包装不下:
当背包容量j小于当前第i个物品重量W(i) 时,即j<W(i) 判断为装不下,此时的最大价值X(i,j) 与前一个X(i-1,j) 的最大价值一样,即X(i,j)=X(i-1,j)。
-
背包装得下:
当背包容量j大于等于当前第i个物品重量W(i) 时,判断要不要装进背包。
2.1:装入当前物品时的最大价值Value1:
背包总容量j减去当前物品的重量W(i) 后,获取剩余总容量的上一物品最大价值X(i-1,j-W(i)) 与当前物品的价值V(i) 相加,即 Value1=X(i-1,j-W(i)) + V(i) 。2.2:不装当前物品时的最大价值Value2:
前一个物品i-1在此背包总容量j情景下的最大价值X(i-1,j),即 Value2=X(i-1,j) 。
Value1-Value2 大于0则取当前和值Value1,反之取上一物品此背包总容量情景下的最大价值Value2。
此时不理解上述公式没关系,跟着下面的填数去慢慢理解
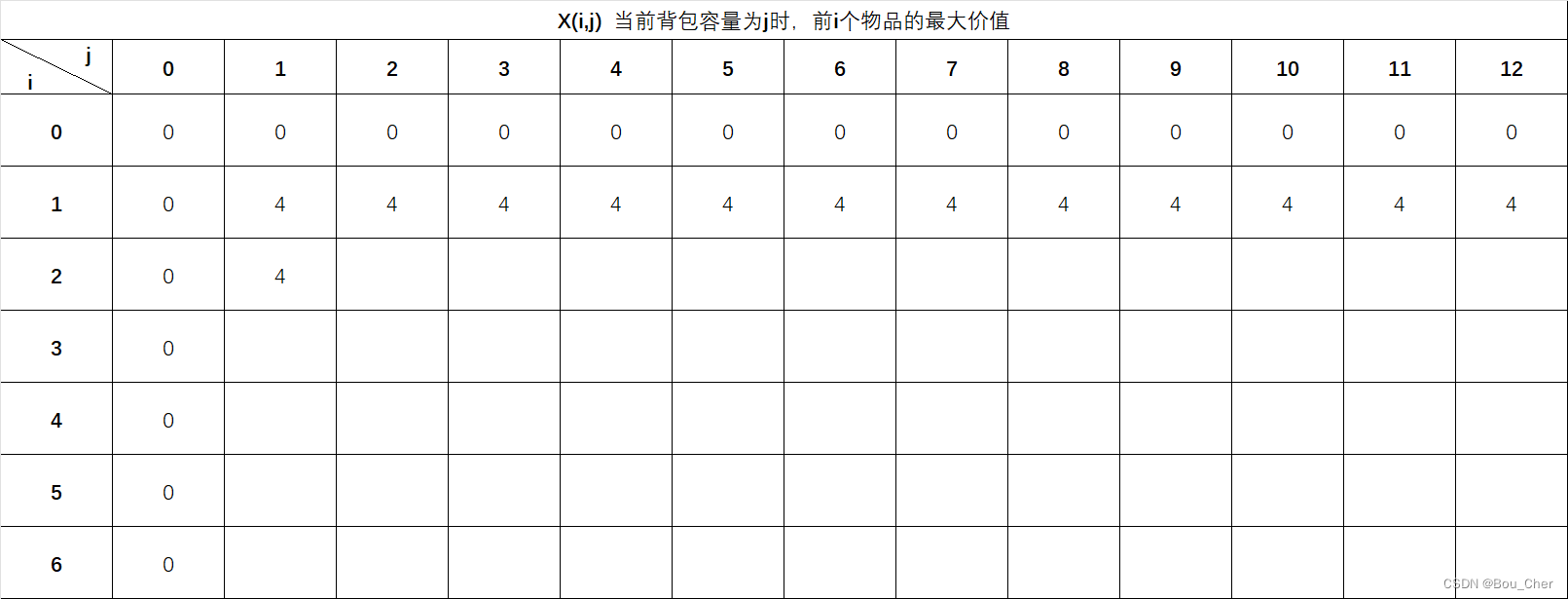
X(2,1) 填数,首先判断背包能否装下:
j=1,W(2)=2,j<W(2),因此当背包容量为1时,物品2装不下,此时最大价值取前一个物品i-1此背包总容量j情景下的最大价值X(i-1,j)=X(2-1,1)=X(1,1)=4,因此X(2,1)=4。
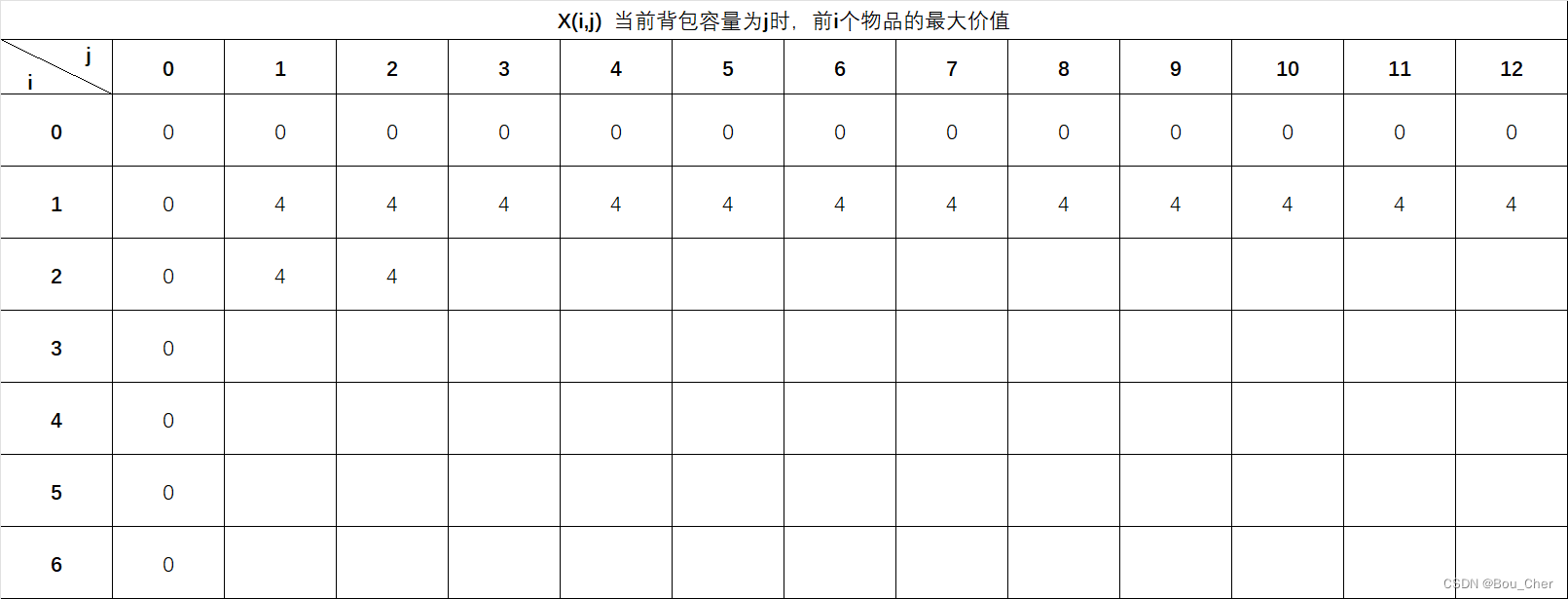
X(2,2) 填数,首先判断背包能否装下:
j=2,W(2)=2,j=W(2),因此当背包容量为2时,物品2装得下。
此时需要判断要不要装物品2:
装入当前物品时的最大价值:Value1 = X(i-1,j-W(i)) + V(i) = X(2-1,2-2) + 1 = X(1,0) + 1 = 0 + 1 = 1。
不装当前物品时的最大价值:Value2 = X(i-1,j) = X(2-1,2) = X(1,2) = 4。
Value1<Value2,因此取上一物品此背包总容量情景下的最大价值,即X(2,2) = X(1,2) = 4。
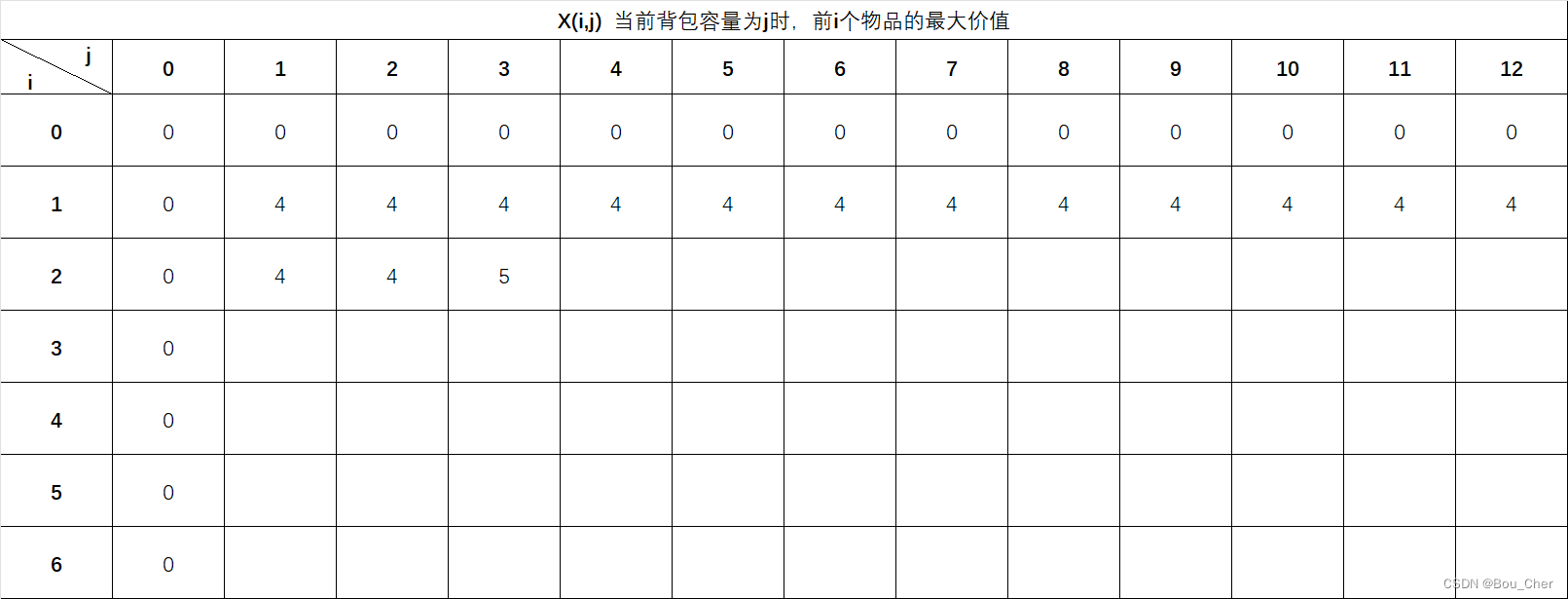
X(2,3) 填数,首先判断背包能否装下:
j=3,W(2)=2,j>W(2),因此当背包容量为3时,物品2装得下。
此时需要判断要不要装物品2:
装入当前物品时的最大价值:Value1 = X(i-1,j-W(i)) + V(i) = X(2-1,3-2) + 1 = X(1,1) + 1 = 4 + 1 = 5。
不装当前物品时的最大价值:Value2 = X(i-1,j) = X(2-1,3) = X(1,3) = 4。
Value1>Value2,因此取当前物品的价值加剩余总容量的最佳价值,即X(2,3) = 5。
按照此规律,我们将表全部填充完毕:
取两个坐标进行验证:
例如1:X(4,3) 填数,首先判断背包能否装下:
j=3,W(4)=3,j=W(4),因此当背包容量为3时,物品4装得下。
此时需要判断要不要装物品4:
装入当前物品时的最大价值:Value1 = X(i-1,j-W(i)) + V(i) = X(4-1,3-3) + 6 = X(3,0) + 6 = 0 + 6 = 6。
不装当前物品时的最大价值:Value2 = X(i-1,j) = X(4-1,3) = X(3,3) = 7。
Value1<Value2,因此取上一物品此背包总容量情景下的最大价值,即X(4,3) = X(3,3) = 7。
例如2:X(4,4) 填数,首先判断背包能否装下:
j=4,W(4)=3,j>W(4),因此当背包容量为4时,物品4装得下。
此时需要判断要不要装物品4:
装入当前物品时的最大价值:Value1 = X(i-1,j-W(i)) + V(i) = X(4-1,4-3) + 6 = X(3,1) + 6 = 4 + 6 = 10。
不装当前物品时的最大价值:Value2 = X(i-1,j) = X(4-1,4) = X(3,4) = 7。
Value1>Value2,因此取当前物品的价值加剩余总容量的最佳价值,即X(4,3) = 10。
代码实现:
int bag = 12; // 背包总容量
int number = 6; // 物品数量
int[] weight = {1, 2, 2, 3, 4, 6}; // 物品重量数组
int[] value = {4, 1, 3, 6, 8, 2}; // 物品价值数组
int[][] max = new int[number + 1][bag + 1]; // 最大价值数组int value1 = 0; // 过渡值:装入当前物品时的最大价值
int value2 = 0; // 过渡值:不装当前物品时的最大价值// 找出最大价值for (int i = 1; i <= number; i++) { // 行for (int j = 1; j <= bag; j++) { // 列// 判断背包能否装得下if (j < weight[i - 1]) { // 装不下max[i][j] = max[i - 1][j]; // 与前一个物品的最大价值相同} else { // 能装下// 前一个物品剩余重量的最大价值+当前物品的价值value1 = max[i - 1][j - weight[i - 1]] + value[i - 1];// 前一个物品当前重量的最大价值value2 = max[i - 1][j];// 取最大值max[i][j] = value1 > value2 ? value1 : value2;}}
}System.out.println(Arrays.deepToString(max)); // 打印最大价值数组
System.out.println("MaxValue = " + max[number][bag]); // 打印最大价值
结果输出:
[[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4],
[0, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5],
[0, 4, 4, 7, 7, 8, 8, 8, 8, 8, 8, 8, 8],
[0, 4, 4, 7, 10, 10, 13, 13, 14, 14, 14, 14, 14],
[0, 4, 4, 7, 10, 12, 13, 15, 18, 18, 21, 21, 22],
[0, 4, 4, 7, 10, 12, 13, 15, 18, 18, 21, 21, 22]]
MaxValue = 22
在上述结果基础上,如果需要知道最大价值情况下,都装入了哪些商品,就需要进行回溯。
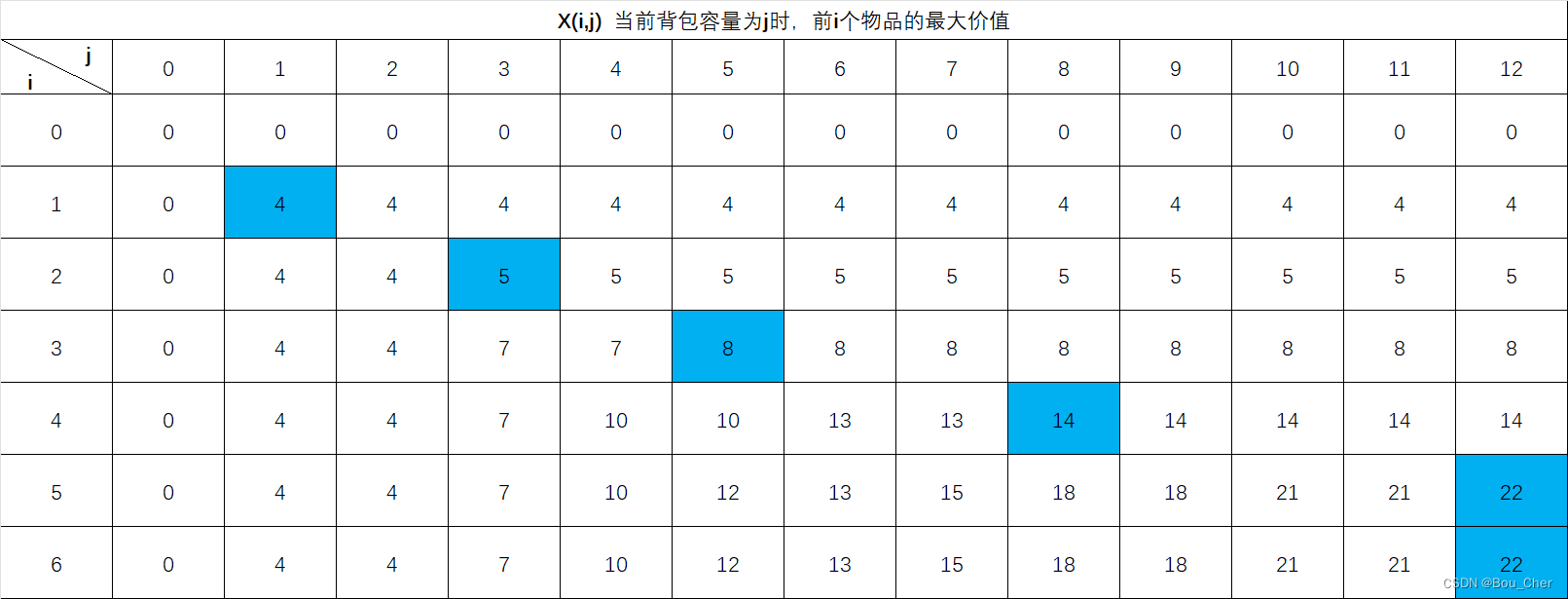
已知X[6][12] 为最大价值,首先判断它有没有装入背包,即X[6][12] = X[6-1][12] 是否生效,若相等,则未装入,继续以X[6-1][12] 作为最大价值进行判断。
X[5][12] 同理与X[5-1][12] 比较,发现不相等,通过公式22 = X[5-1][j-W(5)] + V[5] = X[4][12-4] + 8 = X[4][8] + 8 ,即X[4][8] = 22-8 = 14,反算后值也相等,则第5个物品装入了背包。
以此类推,公式为:
-
未装入背包:
X[i][j] = X[i-1][j],则当前物品未装入背包。 -
转入背包:
X[i-1][j-W(i)] = X[i][j] - V[i],则当前物品装入背包。
代码实现:
List list = new ArrayList<>(); // 装入物品编号// 回溯查找装入物品编号
findNo(number, bag);
Collections.sort(list); // 按照物品编号排序
System.out.println(list.toString());void findNo(int i, int j) {if (i > 0) {// 判断是否装入背包if (max[i][j] == max[i - 1][j]) {// 与上一物品最大价值相等,当前物品未装入findNo(i - 1, j);} else if (j - weight[i-1] >= 0 && (max[i - 1][j - weight[i-1]] == max[i][j] - value[i-1])) { // 与上一物品最大价值不相等且反算成功,当前物品装入,继续递归list.add(i);findNo(i - 1, j - weight[i-1]);}}
}
结果输出:
[1, 2, 3, 4, 5]
相关文章:

动态规划 背包问题
动态规划 背包问题 问题描述: 有一个背包,总容量为12。有6件物品,每件物品的重量和价值不同,求在背包总容量12的前提下,装进物品的最大价值以及装进物品的编号 单个物品重量和价值: 为方便进行思考&#…...
—— 内存模型和名称空间)
C++ Primer Plus 学习笔记(四)—— 内存模型和名称空间
1 单独编译 C允许将组件函数放在独立的文件即头文件中,头文件中可以包含以下内容: 函数原型;使用#define或const定义的符号常量;结构声明;类声明;模板声明;内联函数。 注意,在包含…...
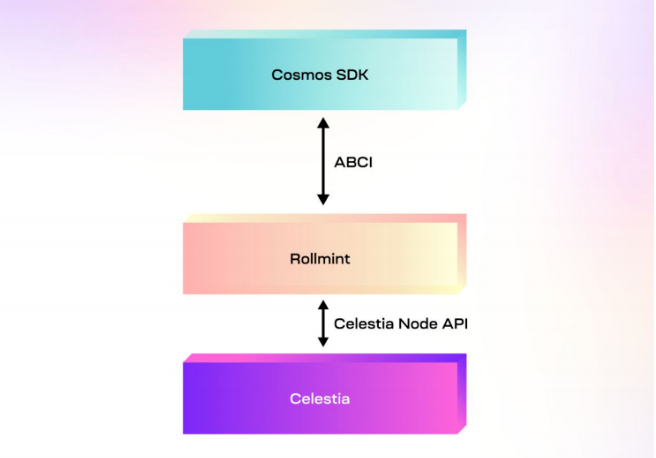
详解基于 Celestia、Eclipse 构建的首个Layer3 链 Nautilus Chain
以流支付为主要概念的Zebec生态,正在推动流支付这种新兴的支付方式向更远的方向发展,该生态最初以Zebec Protocol的形态发展,并从初期的Solana进一步拓展至BNB Chian以及Near上。与此同时,Zebec生态也在积极的寻求从协议形态向公链…...

列表与数组的转化
目录用np.array(a)将列表转换为数组列表转数组的特殊情况(一)列表转数组的特殊情况(二)针对子元素个数不一致的解决办法用a.tolist()函数将数组转化为列表在python的学习中,经常会用到数组与列表的相互转化,本文主要介绍下关于数组与列表转化的问题。用n…...
docker 运行花生壳实现内外网穿透
环境:centos 7 ,64位 1、创建一个指定的文件夹作为安装示例所用,该示例文件夹为“hsk-nwct”。“hsk-nwct”内创建“app”文件夹作为docker容器挂载出来的文件。 2、在“app”内下载花生壳linux安装包,下载花生壳应用:花生壳客户…...
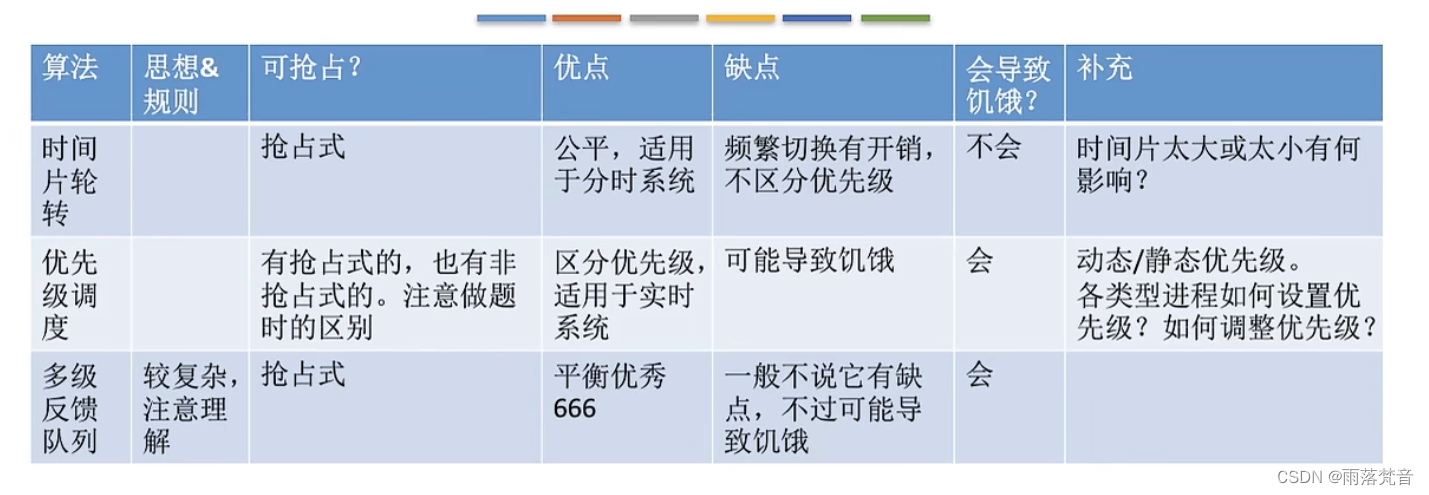
操作系统——16.时间片轮转、优先级、多级反馈队列算法
这篇文章我们来看一下进程调度算法中的时间片轮转、优先级、多级反馈队列算法 目录 1.概述 2.时间片轮转调度算法(RR,Round-Robin) 3.优先级调度算法 4.多级反馈队列调度算法 5.分析对比 1.概述 首先,我们来看一下这篇文章…...

Python3.8.8-Django3.2-Redis-连接池-数据类型-字符串-list-hashmap-命令行操作
文章目录1.认识Redis1.1.优点1.2.缺点2.在Django中Redis的连接3.Redis的基础用法3.1.hashmap结构3.2.list结构4.命令行查看数据库5.作者答疑1.认识Redis Remote DIctionary Server(Redis) 是一个key-value 存储系统,是跨平台的非关系型数据库。是一个开源的使用 AN…...

Android kotlin 系列讲解(进阶篇)高级项目架构模式 - MVVM
<<返回总目录 1、MVVM是什么 MVVM是Model-View-ViewModel的缩写,是一种高级项目架构模式。 MVVM架构可以将程序结构主要分成三个部分: Model:数据模型部分,包括从服务端获取的json数据或者从本地获取的数据等等View&…...

8. 查找
1 题目描述 查找成绩10开启时间2021年09月24日 星期五 18:00折扣0.8折扣时间2021年11月15日 星期一 00:00允许迟交否关闭时间2021年11月23日 星期二 00:00 输入 n(n ≤ 10^6)个不超过 10^9的单调不减的(就是后面的数字不小于前面的数字)非负整数 &#…...

二分查找算法
感谢“五点七边”工作室的算法讲解,详细内容可以参考视频讲解 二分查找为什么总是写错?_哔哩哔哩_bilibili 此处仅是个人学习总结 以target等于5为例,输入: 1 2 3 5 5 5 8 9 1. 找到第一个 > target 的元素 判断条件 < target&am…...
之远程服务器)
Git(3)之远程服务器
Git基础之远程服务器 Author:onceday date:2023年3月5日 满满长路有人对你微笑过嘛… windows安装可参考文章:git简易配置_onceday_CSDN博客 參考文档: 《progit2.pdf》,Progit2 Github。《git-book.pdf》 文章目…...
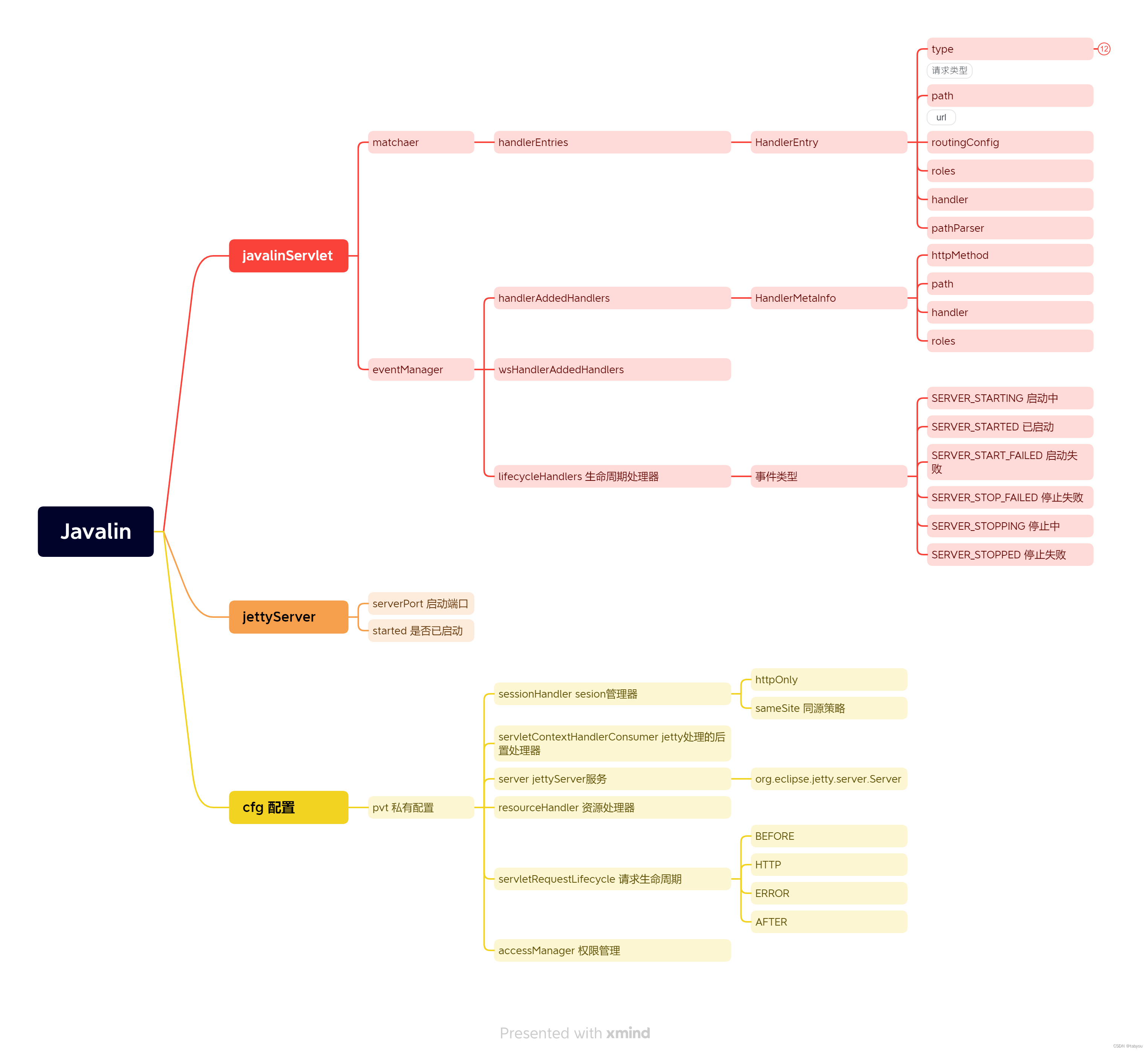
Javalin解构
Javalin Javalin是一个轻量级http框架,我们可以很容易的了解请求的处理过程及其设计,具有较高的学习意义。 从demo说起 public static void main(String[] args) {Javalin app Javalin.create(config -> {System.out.println("用户配置"…...
yolov5算法,训练模型,模型检测
嘟嘟嘟嘟!工作需要,所以学习了下yolov5算法。是干什么的呢? 通俗来说,可以将它看做是一个小孩儿,通过成年人(开发人员)提供的大量图片的学习,让自己知道我看到的哪些场景需要提醒给成…...

linux系统防火墙开放端口
linux系统防火墙开放端口 在外部访问CentOS中部署应用时,需要通过防火墙管理软件,开端口,或者直接关闭防火墙进行解决(不建议) 加粗样式 常用命令: systemctl start firewalld #启动 systemctl stop firewalld #停止 systemctl status firewalld #查看…...

CSAPP第九章 虚拟内存
理解虚拟内存的原因 本章前部分描述虚拟内存是如何工作的,后一部分描述应用程序如何使用和管理虚拟内存 物理和虚拟寻址 虚拟内存作为缓存的工具 页表 页命中 缺页 虚拟内存作为内存管理的工具 简化链接,简化加载,简化共享,简化…...
)
numpy数组与矩阵运算(二)
文章目录矩阵生成与常用操作矩阵生成矩阵转置查看矩阵特性矩阵乘法计算相关系数矩阵计算方差、协方差、标准差计算特征值与特征向量计算逆矩阵求解线性方程组奇异值分解函数向量化矩阵生成与常用操作 矩阵生成 扩展库numpy中提供的matrix()函数可以用来把列表、元组、range对…...

Dubbo 中 Zookeeper 注册中心原理分析
Dubbo 中 Zookeeper 注册中心原理分析 文章目录Dubbo 中 Zookeeper 注册中心原理分析一、ZooKeeper注册中心1.1 ZooKeeper数据结构1.2 ZooKeeper的Watcher机制1.3 ZooKeeper会话机制1.4 使用ZooKeeper作为注册中心二、源码分析2.1 AbstractRegistry2.2 FailbackRegistry2.2.1 核…...
--哥德巴赫猜想的第一次实际应用)
素数产生新的算法(由筛法减法改为增加法)--哥德巴赫猜想的第一次实际应用
素数产生新的算法(由筛法减法改为增加法)--哥德巴赫猜想的第一次实际应用 摘要:长期以来,人们认为哥德巴赫猜想没有什么实际应用的。 现在,我假设这个不是猜想,而是定理或公理,就产生了新的应用…...

递归-需要满足三个条件
一,概述 递归是一种应用非常广泛的算法(或者编程技巧)。很多数据结构和算法的编码实现都要用到递归,比如 DFS 深度优先搜索、前中后序二叉树遍历等。 去的过程叫“递”,回来的过程叫“归”。基本上所有的递归问题都可…...

【剑指Offer-Java】两个栈实现队列
题目 用两个栈实现一个队列。队列的声明如下,请实现它的两个函数 appendTail 和 deleteHead ,分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素,deleteHead 操作返回 -1 ) 输入: [“CQueue”,“appendT…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...
