【LeetCode】剑指 Offer(16)
目录
题目:剑指 Offer 33. 二叉搜索树的后序遍历序列 - 力扣(Leetcode)
题目的接口:
解题思路:
代码:
过啦!!!
写在最后:
题目:剑指 Offer 33. 二叉搜索树的后序遍历序列 - 力扣(Leetcode)
题目的接口:
class Solution {
public:bool verifyPostorder(vector<int>& postorder) {}
};解题思路:
我一般做二叉树的遍历的题目,
用的都是递归法,
这里二叉搜索树有一个特点:左子树小于根节点,右子树大于根节点
我们就利用这个特性来判断数组是不是二叉搜索树的后序遍历。
大体思路就是判断:
左子树是否小于根节点,右子树是否大于根节点,
遍历过程中找到左子树和右子树的边界,
再以每个左子树和右子树作为子集,
递归遍历每一个子集,如果符合条件就返回 true,不符合就返回 false。
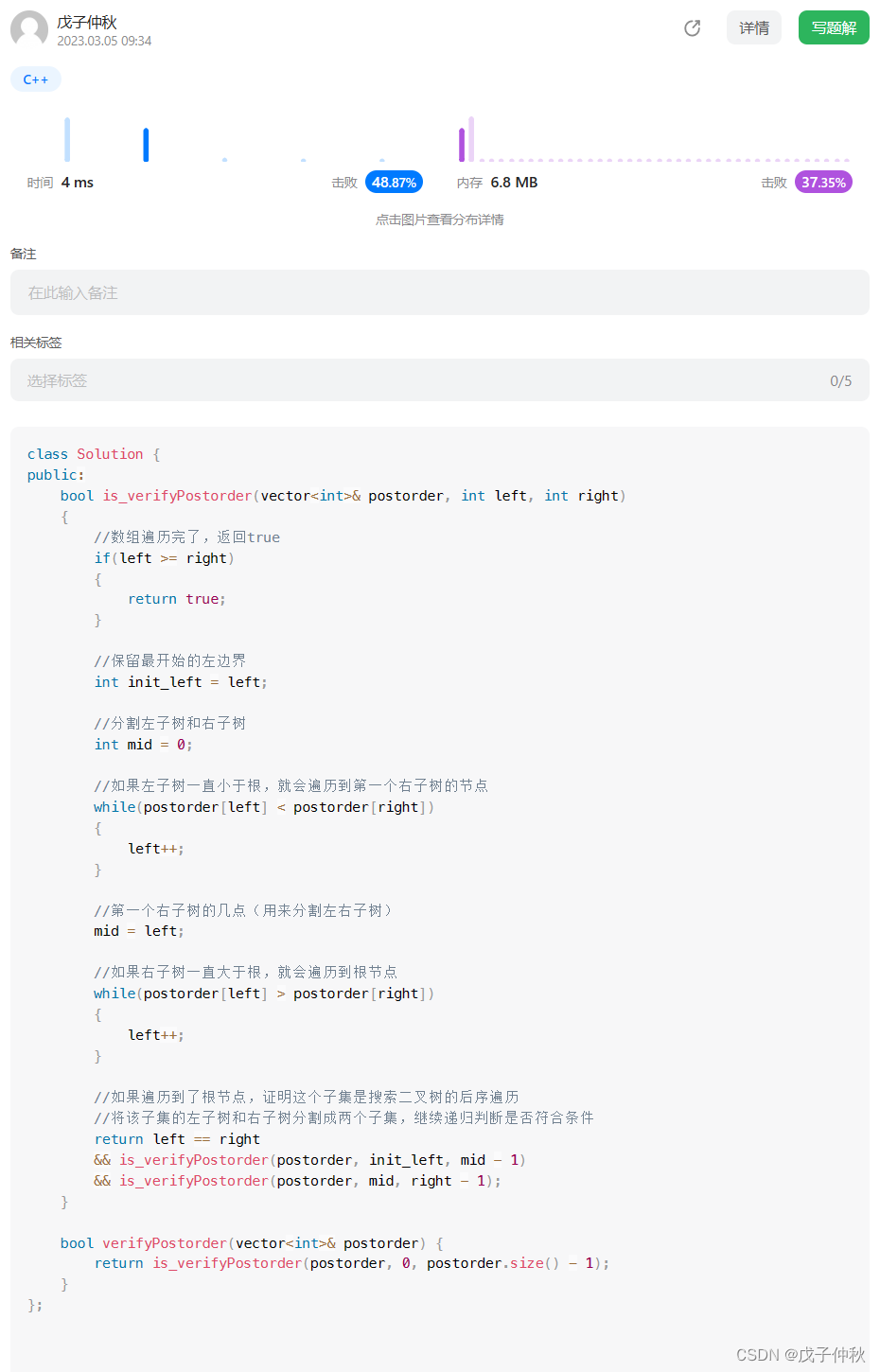
代码:
class Solution {
public:bool is_verifyPostorder(vector<int>& postorder, int left, int right){//数组遍历完了,返回trueif(left >= right){return true;}//保留最开始的左边界int init_left = left;//分割左子树和右子树int mid = 0;//如果左子树一直小于根,就会遍历到第一个右子树的节点while(postorder[left] < postorder[right]){left++;}//第一个右子树的几点(用来分割左右子树)mid = left;//如果右子树一直大于根,就会遍历到根节点while(postorder[left] > postorder[right]){left++;}//如果遍历到了根节点,证明这个子集是搜索二叉树的后序遍历//将该子集的左子树和右子树分割成两个子集,继续递归判断是否符合条件return left == right && is_verifyPostorder(postorder, init_left, mid - 1)&& is_verifyPostorder(postorder, mid, right - 1);}bool verifyPostorder(vector<int>& postorder) {return is_verifyPostorder(postorder, 0, postorder.size() - 1);}
};过啦!!!
写在最后:
以上就是本篇文章的内容了,感谢你的阅读。
如果喜欢本文的话,欢迎点赞和评论,写下你的见解。
如果想和我一起学习编程,不妨点个关注,我们一起学习,一同成长。
之后我还会输出更多高质量内容,欢迎收看。
相关文章:

【LeetCode】剑指 Offer(16)
目录 题目:剑指 Offer 33. 二叉搜索树的后序遍历序列 - 力扣(Leetcode) 题目的接口: 解题思路: 代码: 过啦!!! 写在最后: 题目:剑指 Offer …...
)
第三十九章 linux-并发解决方法二(互斥锁mutex)
第三十九章 linux-并发解决方法二(互斥锁mutex) 文章目录第三十九章 linux-并发解决方法二(互斥锁mutex)互斥锁的定义与初始化互斥锁的DOWN操作互斥锁的UP操作用count1的信号量实现的互斥方法还不是Linux下经典的用法,…...

脚本方式本地仓库jar包批量导入maven私服
脚本内容,将以下内容保存为mavenimport.sh,放置于需要上传的目录下,可以是顶层目录,或者某个分包的目录,若私服已有待上传的包,则执行会被替换 #!/bin/bash # copy and run this script to the root of th…...

【c++】引用的学习
引用的定义和声明 引用是一种别名,它允许使用与原变量相同的内存位置。在C中,引用是使用&符号来定义的。引用必须在定义时初始化,并且可以与原变量分别使用。 int a 10; int& b a; // 定义了一个引用b,它指向a引用的作用…...

linux 软件安装及卸载
1.联网在线安装及卸载ubuntu环境下:使用apt-get 工具apt-get install - 安装软件包apt-get remove - 移除(卸载)软件包CentOS环境下:使用yum工具 (银河麒麟系统属于centos)yum install - 安装软件包yum rem…...
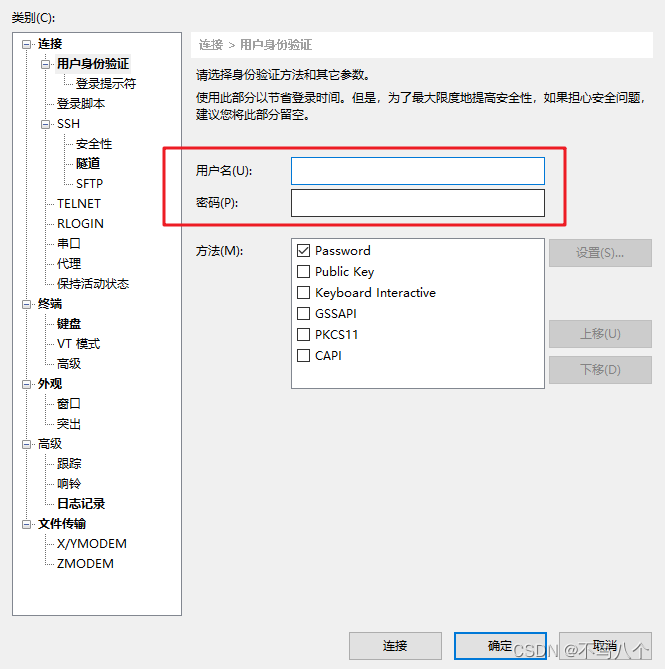
XShell连接ubuntu20.04.LTS
1 下载XshellXShell官方下载地址打开XSHELL官方下载地址,我们可以选择【家庭和学校用户的免费许可证】,输入邮箱之后即可获得下载链接安装非常简单,跟着提示进行即可。2 连接ubuntu2.1 查看ubuntu的ip地址输入命令查看ip地址ifconfig刚开始可…...

【FPGA】Verilog:MSI/LSI 组合电路之解码器 | 多路分解器
写在前面:本章将理解编码器与解码器、多路复用器与多路分解器的概念,通过使用 Verilog 实现多样的解码器与多路分解器,通过 FPGA 并使用 Verilog 实现。 Ⅰ. 前置知识 0x00 解码器与编码器(Decoder / Encoder) 解码器…...

深入理解JDK动态代理原理,使用javassist动手写一个动态代理框架
文章目录一、动手实现一个动态代理框架1、初识javassist2、使用javassist实现一个动态代理框架二、JDK动态代理1、编码实现2、基本原理(1)getProxyClass0方法(2)总结写在后面一、动手实现一个动态代理框架 1、初识javassist Jav…...
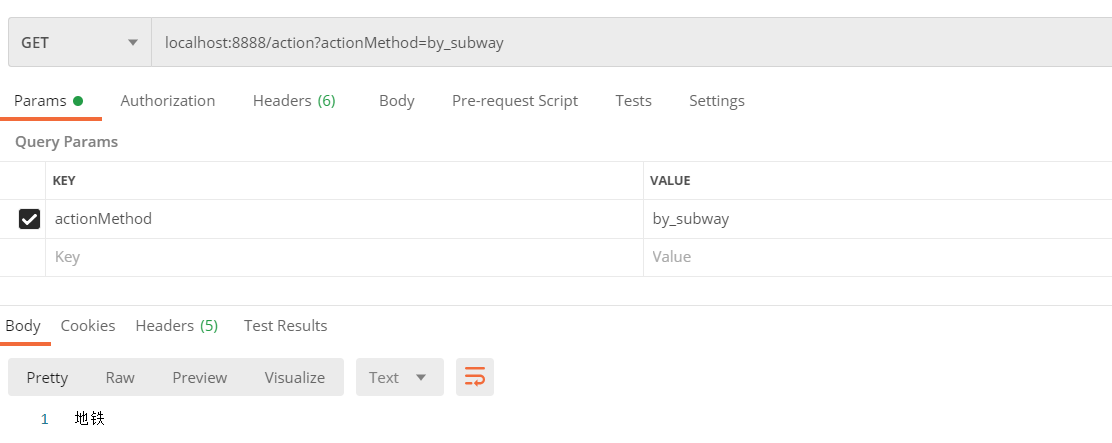
一、策略模式的使用
1、策略模式定义: 策略模式(Strategy Pattern)定义了一组策略,分别在不同类中封装起来,每种策略都可以根据当前场景相互替换,从而使策略的变化可以独立于操作者。比如我们要去某个地方,会根据距…...

Verilog使用always块实现时序逻辑
这篇文章将讨论 verilog 中一个重要的结构---- always 块(always block)。verilog 中可以实现的数字电路主要分为两类----组合逻辑电路和时序逻辑电路。与组合逻辑电路相反,时序电路电路使用时钟并一定需要触发器等存储元件。因此,…...
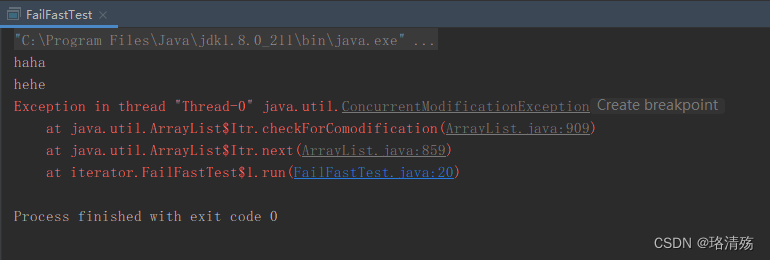
面向对象设计模式:行为型模式之迭代器模式
一、迭代器模式,Iterator Pattern aka:Cursor Pattern 1.1 Intent 意图 Provide a way to access the elements of an aggregate object sequentially without exposing its underlying representation. 提供一种按顺序访问聚合对象的元素而不公开其基…...
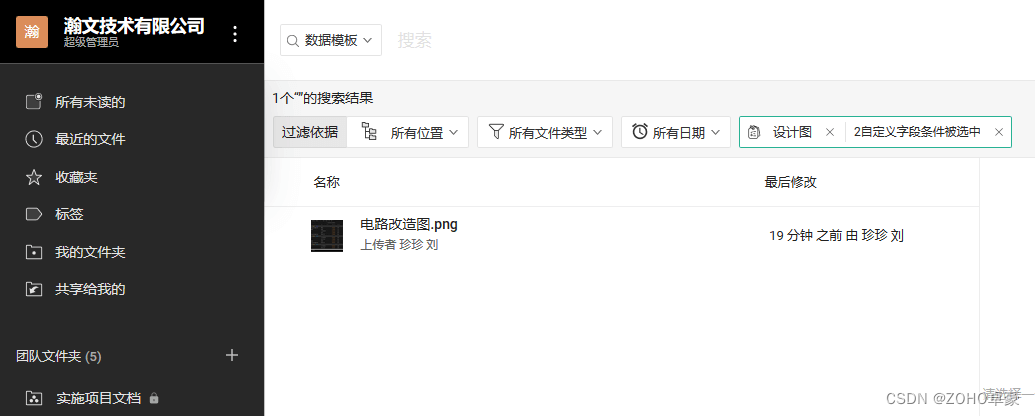
如何快速在企业网盘中找到想要的文件
现在越来越多的企业采用企业网盘来存储文档和资料,而且现在市面上的企业网盘各种各样。在使用企业网盘过程中,很多用户会问到企业网盘中如何快速搜索文件的问题。但是无论是“标签”功能还是普通的“关键词搜索”功能,都是单层级的࿰…...
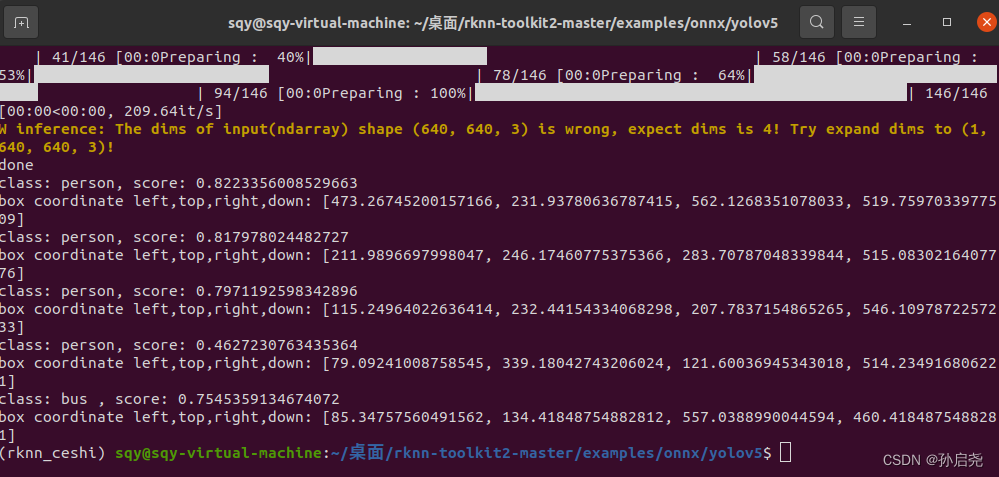
香橙派5使用NPU加速yolov5的实时视频推理(二)
三、将best.onnx转为RKNN格式 这一步就需要我们进入到Ubuntu20.04系统中了,我的Ubuntu系统中已经下载好了anaconda,使用anaconda的好处就是可以方便的安装一些库,而且还可以利用conda来配置虚拟环境,做到环境与环境之间相互独立。…...
)
算法练习-二分查找(一)
算法练习-二分查找 1 代码实现 1.1 非递归实现 public int bsearch(int[] a, int n, int value) {int low 0;int high n - 1;while (low < high) {int mid (low high) / 2;if (a[mid] value) {return mid;} else if (a[mid] < value) {low mid 1} else {high …...
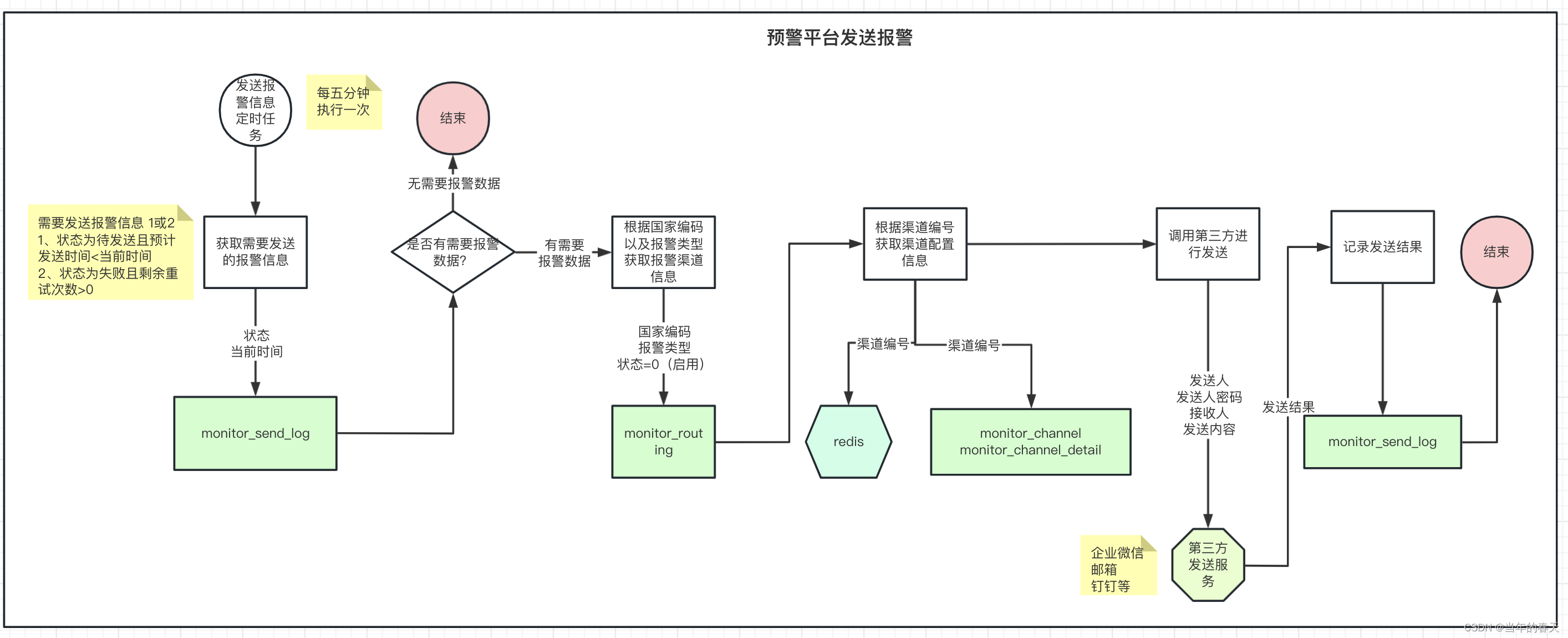
通用业务平台设计(五):预警平台建设
前言 在上家公司,随着业务的不断拓展(从支持单个国家单个主体演变成支持多个国家多个主体),对预警的诉求越来越紧迫;如何保障业务的稳定性那?预警可以帮我们提前甄别风险,从而让我们可以在风险来临前将其消灭ÿ…...

Windows openssl-1.1.1d vs2017编译
工具: 1. perl(https://strawberryperl.com/) 2. nasm(https://nasm.us/) 3. openssl源码(https://www.openssl.org/) 可以自己去下载 或者我的网盘提供下载: 链接:…...

【深蓝学院】手写VIO第2章--IMU传感器--笔记
0. 内容 1. 旋转运动学 角速度的推导: 左ω∧\omega^{\wedge}ω∧,而ω\omegaω是在z轴方向运动,θ′[0,0,1]T\theta^{\prime}[0,0,1]^Tθ′[0,0,1]T 两边取模后得到结论: 线速度大小半径 * 角速度大小 其中,对旋转矩…...
网络基础(二)之HTTP与HTTPS
应用层 再谈 "协议" 协议是一种 "约定". socket api的接口, 在读写数据时, 都是按 "字符串" 的方式来发送接收的. 如果我们要传输一些"结构化的数据" 怎么办呢? 为什么要转换呢? 如果我们将struct message里面的信息…...

Python每日一练(20230306)
目录 1. 翻转二叉树 ★★ 2. 最长公共前缀 ★★ 3. 2的幂 ★ 1. 翻转二叉树 翻转一棵二叉树。 示例 1: 输入: 4/ \2 7/ \ / \ 1 3 6 9 输出: 4/ \7 2/ \ / \ 9 6 3 1示例 2: 输入: 1…...

C/C++每日一练(20230305)
目录 1. 整数分解 ☆ 2. 二叉树的最小深度 ★★ 3. 找x ★★ 1. 整数分解 输入一个正整数,将其按7进制位分解为各乘式的累加和。 示例 1: 输入:49 输出:497^2示例 2: 输入:720 输出:720…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...
