【深度学习笔记】优化算法——随机梯度下降
随机梯度下降
在前面的章节中,我们一直在训练过程中使用随机梯度下降,但没有解释它为什么起作用。为了澄清这一点,我们刚在 :numref:sec_gd中描述了梯度下降的基本原则。本节继续更详细地说明随机梯度下降(stochastic gradient descent)。
%matplotlib inline
import math
import torch
from d2l import torch as d2l
随机梯度更新
在深度学习中,目标函数通常是训练数据集中每个样本的损失函数的平均值。给定 n n n个样本的训练数据集,我们假设 f i ( x ) f_i(\mathbf{x}) fi(x)是关于索引 i i i的训练样本的损失函数,其中 x \mathbf{x} x是参数向量。然后我们得到目标函数
f ( x ) = 1 n ∑ i = 1 n f i ( x ) . f(\mathbf{x}) = \frac{1}{n} \sum_{i = 1}^n f_i(\mathbf{x}). f(x)=n1i=1∑nfi(x).
x \mathbf{x} x的目标函数的梯度计算为
∇ f ( x ) = 1 n ∑ i = 1 n ∇ f i ( x ) . \nabla f(\mathbf{x}) = \frac{1}{n} \sum_{i = 1}^n \nabla f_i(\mathbf{x}). ∇f(x)=n1i=1∑n∇fi(x).
如果使用梯度下降法,则每个自变量迭代的计算代价为 O ( n ) \mathcal{O}(n) O(n),它随 n n n线性增长。因此,当训练数据集较大时,每次迭代的梯度下降计算代价将较高。
随机梯度下降(SGD)可降低每次迭代时的计算代价。在随机梯度下降的每次迭代中,我们对数据样本随机均匀采样一个索引 i i i,其中 i ∈ { 1 , … , n } i\in\{1,\ldots, n\} i∈{1,…,n},并计算梯度 ∇ f i ( x ) \nabla f_i(\mathbf{x}) ∇fi(x)以更新 x \mathbf{x} x:
x ← x − η ∇ f i ( x ) , \mathbf{x} \leftarrow \mathbf{x} - \eta \nabla f_i(\mathbf{x}), x←x−η∇fi(x),
其中 η \eta η是学习率。我们可以看到,每次迭代的计算代价从梯度下降的 O ( n ) \mathcal{O}(n) O(n)降至常数 O ( 1 ) \mathcal{O}(1) O(1)。此外,我们要强调,随机梯度 ∇ f i ( x ) \nabla f_i(\mathbf{x}) ∇fi(x)是对完整梯度 ∇ f ( x ) \nabla f(\mathbf{x}) ∇f(x)的无偏估计,因为
E i ∇ f i ( x ) = 1 n ∑ i = 1 n ∇ f i ( x ) = ∇ f ( x ) . \mathbb{E}_i \nabla f_i(\mathbf{x}) = \frac{1}{n} \sum_{i = 1}^n \nabla f_i(\mathbf{x}) = \nabla f(\mathbf{x}). Ei∇fi(x)=n1i=1∑n∇fi(x)=∇f(x).
这意味着,平均而言,随机梯度是对梯度的良好估计。
现在,我们将把它与梯度下降进行比较,方法是向梯度添加均值为0、方差为1的随机噪声,以模拟随机梯度下降。
def f(x1, x2): # 目标函数return x1 ** 2 + 2 * x2 ** 2def f_grad(x1, x2): # 目标函数的梯度return 2 * x1, 4 * x2
def sgd(x1, x2, s1, s2, f_grad):g1, g2 = f_grad(x1, x2)# 模拟有噪声的梯度g1 += torch.normal(0.0, 1, (1,)).item()g2 += torch.normal(0.0, 1, (1,)).item()eta_t = eta * lr()return (x1 - eta_t * g1, x2 - eta_t * g2, 0, 0)
def constant_lr():return 1eta = 0.1
lr = constant_lr # 常数学习速度
d2l.show_trace_2d(f, d2l.train_2d(sgd, steps=50, f_grad=f_grad))
epoch 50, x1: 0.020569, x2: 0.227895

正如我们所看到的,随机梯度下降中变量的轨迹比我们在 :numref:sec_gd中观察到的梯度下降中观察到的轨迹嘈杂得多。这是由于梯度的随机性质。也就是说,即使我们接近最小值,我们仍然受到通过 η ∇ f i ( x ) \eta \nabla f_i(\mathbf{x}) η∇fi(x)的瞬间梯度所注入的不确定性的影响。即使经过50次迭代,质量仍然不那么好。更糟糕的是,经过额外的步骤,它不会得到改善。这给我们留下了唯一的选择:改变学习率 η \eta η。但是,如果我们选择的学习率太小,我们一开始就不会取得任何有意义的进展。另一方面,如果我们选择的学习率太大,我们将无法获得一个好的解决方案,如上所示。解决这些相互冲突的目标的唯一方法是在优化过程中动态降低学习率。
这也是在sgd步长函数中添加学习率函数lr的原因。在上面的示例中,学习率调度的任何功能都处于休眠状态,因为我们将相关的lr函数设置为常量。
动态学习率
用与时间相关的学习率 η ( t ) \eta(t) η(t)取代 η \eta η增加了控制优化算法收敛的复杂性。特别是,我们需要弄清 η \eta η的衰减速度。如果太快,我们将过早停止优化。如果减少的太慢,我们会在优化上浪费太多时间。以下是随着时间推移调整 η \eta η时使用的一些基本策略(稍后我们将讨论更高级的策略):
η ( t ) = η i if t i ≤ t ≤ t i + 1 分段常数 η ( t ) = η 0 ⋅ e − λ t 指数衰减 η ( t ) = η 0 ⋅ ( β t + 1 ) − α 多项式衰减 \begin{aligned} \eta(t) & = \eta_i \text{ if } t_i \leq t \leq t_{i+1} && \text{分段常数} \\ \eta(t) & = \eta_0 \cdot e^{-\lambda t} && \text{指数衰减} \\ \eta(t) & = \eta_0 \cdot (\beta t + 1)^{-\alpha} && \text{多项式衰减} \end{aligned} η(t)η(t)η(t)=ηi if ti≤t≤ti+1=η0⋅e−λt=η0⋅(βt+1)−α分段常数指数衰减多项式衰减
在第一个分段常数(piecewise constant)场景中,我们会降低学习率,例如,每当优化进度停顿时。这是训练深度网络的常见策略。或者,我们可以通过指数衰减(exponential decay)来更积极地减低它。不幸的是,这往往会导致算法收敛之前过早停止。一个受欢迎的选择是 α = 0.5 \alpha = 0.5 α=0.5的多项式衰减(polynomial decay)。在凸优化的情况下,有许多证据表明这种速率表现良好。
让我们看看指数衰减在实践中是什么样子。
def exponential_lr():# 在函数外部定义,而在内部更新的全局变量global tt += 1return math.exp(-0.1 * t)t = 1
lr = exponential_lr
d2l.show_trace_2d(f, d2l.train_2d(sgd, steps=1000, f_grad=f_grad))
epoch 1000, x1: -0.998659, x2: 0.023408

正如预期的那样,参数的方差大大减少。但是,这是以未能收敛到最优解 x = ( 0 , 0 ) \mathbf{x} = (0, 0) x=(0,0)为代价的。即使经过1000个迭代步骤,我们仍然离最优解很远。事实上,该算法根本无法收敛。另一方面,如果我们使用多项式衰减,其中学习率随迭代次数的平方根倒数衰减,那么仅在50次迭代之后,收敛就会更好。
def polynomial_lr():# 在函数外部定义,而在内部更新的全局变量global tt += 1return (1 + 0.1 * t) ** (-0.5)t = 1
lr = polynomial_lr
d2l.show_trace_2d(f, d2l.train_2d(sgd, steps=50, f_grad=f_grad))
epoch 50, x1: -0.174174, x2: -0.000615

关于如何设置学习率,还有更多的选择。例如,我们可以从较小的学习率开始,然后使其迅速上涨,再让它降低,尽管这会更慢。我们甚至可以在较小和较大的学习率之间切换。现在,让我们专注于可以进行全面理论分析的学习率计划,即凸环境下的学习率。对一般的非凸问题,很难获得有意义的收敛保证,因为总的来说,最大限度地减少非线性非凸问题是NP困难的。有关的研究调查,请参阅例如2015年Tibshirani的优秀讲义笔记。
凸目标的收敛性分析
以下对凸目标函数的随机梯度下降的收敛性分析是可选读的,主要用于传达对问题的更多直觉。我们只限于最简单的证明之一 :cite:Nesterov.Vial.2000。存在着明显更先进的证明技术,例如,当目标函数表现特别好时。
假设所有 ξ \boldsymbol{\xi} ξ的目标函数 f ( ξ , x ) f(\boldsymbol{\xi}, \mathbf{x}) f(ξ,x)在 x \mathbf{x} x中都是凸的。更具体地说,我们考虑随机梯度下降更新:
x t + 1 = x t − η t ∂ x f ( ξ t , x ) , \mathbf{x}_{t+1} = \mathbf{x}_{t} - \eta_t \partial_\mathbf{x} f(\boldsymbol{\xi}_t, \mathbf{x}), xt+1=xt−ηt∂xf(ξt,x),
其中 f ( ξ t , x ) f(\boldsymbol{\xi}_t, \mathbf{x}) f(ξt,x)是训练样本 f ( ξ t , x ) f(\boldsymbol{\xi}_t, \mathbf{x}) f(ξt,x)的目标函数: ξ t \boldsymbol{\xi}_t ξt从第 t t t步的某个分布中提取, x \mathbf{x} x是模型参数。用
R ( x ) = E ξ [ f ( ξ , x ) ] R(\mathbf{x}) = E_{\boldsymbol{\xi}}[f(\boldsymbol{\xi}, \mathbf{x})] R(x)=Eξ[f(ξ,x)]
表示期望风险, R ∗ R^* R∗表示对于 x \mathbf{x} x的最低风险。最后让 x ∗ \mathbf{x}^* x∗表示最小值(我们假设它存在于定义 x \mathbf{x} x的域中)。在这种情况下,我们可以跟踪时间 t t t处的当前参数 x t \mathbf{x}_t xt和风险最小化器 x ∗ \mathbf{x}^* x∗之间的距离,看看它是否随着时间的推移而改善:
∥ x t + 1 − x ∗ ∥ 2 = ∥ x t − η t ∂ x f ( ξ t , x ) − x ∗ ∥ 2 = ∥ x t − x ∗ ∥ 2 + η t 2 ∥ ∂ x f ( ξ t , x ) ∥ 2 − 2 η t ⟨ x t − x ∗ , ∂ x f ( ξ t , x ) ⟩ . \begin{aligned} &\|\mathbf{x}_{t+1} - \mathbf{x}^*\|^2 \\ =& \|\mathbf{x}_{t} - \eta_t \partial_\mathbf{x} f(\boldsymbol{\xi}_t, \mathbf{x}) - \mathbf{x}^*\|^2 \\ =& \|\mathbf{x}_{t} - \mathbf{x}^*\|^2 + \eta_t^2 \|\partial_\mathbf{x} f(\boldsymbol{\xi}_t, \mathbf{x})\|^2 - 2 \eta_t \left\langle \mathbf{x}_t - \mathbf{x}^*, \partial_\mathbf{x} f(\boldsymbol{\xi}_t, \mathbf{x})\right\rangle. \end{aligned} ==∥xt+1−x∗∥2∥xt−ηt∂xf(ξt,x)−x∗∥2∥xt−x∗∥2+ηt2∥∂xf(ξt,x)∥2−2ηt⟨xt−x∗,∂xf(ξt,x)⟩.
:eqlabel:eq_sgd-xt+1-xstar
我们假设随机梯度 ∂ x f ( ξ t , x ) \partial_\mathbf{x} f(\boldsymbol{\xi}_t, \mathbf{x}) ∂xf(ξt,x)的 L 2 L_2 L2范数受到某个常数 L L L的限制,因此我们有
η t 2 ∥ ∂ x f ( ξ t , x ) ∥ 2 ≤ η t 2 L 2 . \eta_t^2 \|\partial_\mathbf{x} f(\boldsymbol{\xi}_t, \mathbf{x})\|^2 \leq \eta_t^2 L^2. ηt2∥∂xf(ξt,x)∥2≤ηt2L2.
:eqlabel:eq_sgd-L
我们最感兴趣的是 x t \mathbf{x}_t xt和 x ∗ \mathbf{x}^* x∗之间的距离如何变化的期望。事实上,对于任何具体的步骤序列,距离可能会增加,这取决于我们遇到的 ξ t \boldsymbol{\xi}_t ξt。因此我们需要点积的边界。因为对于任何凸函数 f f f,所有 x \mathbf{x} x和 y \mathbf{y} y都满足 f ( y ) ≥ f ( x ) + ⟨ f ′ ( x ) , y − x ⟩ f(\mathbf{y}) \geq f(\mathbf{x}) + \langle f'(\mathbf{x}), \mathbf{y} - \mathbf{x} \rangle f(y)≥f(x)+⟨f′(x),y−x⟩,按凸性我们有
f ( ξ t , x ∗ ) ≥ f ( ξ t , x t ) + ⟨ x ∗ − x t , ∂ x f ( ξ t , x t ) ⟩ . f(\boldsymbol{\xi}_t, \mathbf{x}^*) \geq f(\boldsymbol{\xi}_t, \mathbf{x}_t) + \left\langle \mathbf{x}^* - \mathbf{x}_t, \partial_{\mathbf{x}} f(\boldsymbol{\xi}_t, \mathbf{x}_t) \right\rangle. f(ξt,x∗)≥f(ξt,xt)+⟨x∗−xt,∂xf(ξt,xt)⟩.
:eqlabel:eq_sgd-f-xi-xstar
将不等式 :eqref:eq_sgd-L和 :eqref:eq_sgd-f-xi-xstar代入 :eqref:eq_sgd-xt+1-xstar我们在时间 t + 1 t+1 t+1时获得参数之间距离的边界,如下所示:
∥ x t − x ∗ ∥ 2 − ∥ x t + 1 − x ∗ ∥ 2 ≥ 2 η t ( f ( ξ t , x t ) − f ( ξ t , x ∗ ) ) − η t 2 L 2 . \|\mathbf{x}_{t} - \mathbf{x}^*\|^2 - \|\mathbf{x}_{t+1} - \mathbf{x}^*\|^2 \geq 2 \eta_t (f(\boldsymbol{\xi}_t, \mathbf{x}_t) - f(\boldsymbol{\xi}_t, \mathbf{x}^*)) - \eta_t^2 L^2. ∥xt−x∗∥2−∥xt+1−x∗∥2≥2ηt(f(ξt,xt)−f(ξt,x∗))−ηt2L2.
:eqlabel:eqref_sgd-xt-diff
这意味着,只要当前损失和最优损失之间的差异超过 η t L 2 / 2 \eta_t L^2/2 ηtL2/2,我们就会取得进展。由于这种差异必然会收敛到零,因此学习率 η t \eta_t ηt也需要消失。
接下来,我们根据 :eqref:eqref_sgd-xt-diff取期望。得到
E [ ∥ x t − x ∗ ∥ 2 ] − E [ ∥ x t + 1 − x ∗ ∥ 2 ] ≥ 2 η t [ E [ R ( x t ) ] − R ∗ ] − η t 2 L 2 . E\left[\|\mathbf{x}_{t} - \mathbf{x}^*\|^2\right] - E\left[\|\mathbf{x}_{t+1} - \mathbf{x}^*\|^2\right] \geq 2 \eta_t [E[R(\mathbf{x}_t)] - R^*] - \eta_t^2 L^2. E[∥xt−x∗∥2]−E[∥xt+1−x∗∥2]≥2ηt[E[R(xt)]−R∗]−ηt2L2.
最后一步是对 t ∈ { 1 , … , T } t \in \{1, \ldots, T\} t∈{1,…,T}的不等式求和。在求和过程中抵消中间项,然后舍去低阶项,可以得到
∥ x 1 − x ∗ ∥ 2 ≥ 2 ( ∑ t = 1 T η t ) [ E [ R ( x t ) ] − R ∗ ] − L 2 ∑ t = 1 T η t 2 . \|\mathbf{x}_1 - \mathbf{x}^*\|^2 \geq 2 \left (\sum_{t=1}^T \eta_t \right) [E[R(\mathbf{x}_t)] - R^*] - L^2 \sum_{t=1}^T \eta_t^2. ∥x1−x∗∥2≥2(t=1∑Tηt)[E[R(xt)]−R∗]−L2t=1∑Tηt2.
:eqlabel:eq_sgd-x1-xstar
请注意,我们利用了给定的 x 1 \mathbf{x}_1 x1,因而可以去掉期望。最后定义
x ˉ = d e f ∑ t = 1 T η t x t ∑ t = 1 T η t . \bar{\mathbf{x}} \stackrel{\mathrm{def}}{=} \frac{\sum_{t=1}^T \eta_t \mathbf{x}_t}{\sum_{t=1}^T \eta_t}. xˉ=def∑t=1Tηt∑t=1Tηtxt.
因为有
E ( ∑ t = 1 T η t R ( x t ) ∑ t = 1 T η t ) = ∑ t = 1 T η t E [ R ( x t ) ] ∑ t = 1 T η t = E [ R ( x t ) ] , E\left(\frac{\sum_{t=1}^T \eta_t R(\mathbf{x}_t)}{\sum_{t=1}^T \eta_t}\right) = \frac{\sum_{t=1}^T \eta_t E[R(\mathbf{x}_t)]}{\sum_{t=1}^T \eta_t} = E[R(\mathbf{x}_t)], E(∑t=1Tηt∑t=1TηtR(xt))=∑t=1Tηt∑t=1TηtE[R(xt)]=E[R(xt)],
根据詹森不等式(令 :eqref:eq_jensens-inequality中 i = t i=t i=t, α i = η t / ∑ t = 1 T η t \alpha_i = \eta_t/\sum_{t=1}^T \eta_t αi=ηt/∑t=1Tηt)和 R R R的凸性使其满足的 E [ R ( x t ) ] ≥ E [ R ( x ˉ ) ] E[R(\mathbf{x}_t)] \geq E[R(\bar{\mathbf{x}})] E[R(xt)]≥E[R(xˉ)],因此,
∑ t = 1 T η t E [ R ( x t ) ] ≥ ∑ t = 1 T η t E [ R ( x ˉ ) ] . \sum_{t=1}^T \eta_t E[R(\mathbf{x}_t)] \geq \sum_{t=1}^T \eta_t E\left[R(\bar{\mathbf{x}})\right]. t=1∑TηtE[R(xt)]≥t=1∑TηtE[R(xˉ)].
将其代入不等式 :eqref:eq_sgd-x1-xstar得到边界
[ E [ x ˉ ] ] − R ∗ ≤ r 2 + L 2 ∑ t = 1 T η t 2 2 ∑ t = 1 T η t , \left[E[\bar{\mathbf{x}}]\right] - R^* \leq \frac{r^2 + L^2 \sum_{t=1}^T \eta_t^2}{2 \sum_{t=1}^T \eta_t}, [E[xˉ]]−R∗≤2∑t=1Tηtr2+L2∑t=1Tηt2,
其中 r 2 = d e f ∥ x 1 − x ∗ ∥ 2 r^2 \stackrel{\mathrm{def}}{=} \|\mathbf{x}_1 - \mathbf{x}^*\|^2 r2=def∥x1−x∗∥2是初始选择参数与最终结果之间距离的边界。简而言之,收敛速度取决于随机梯度标准的限制方式( L L L)以及初始参数值与最优结果的距离( r r r)。请注意,边界由 x ˉ \bar{\mathbf{x}} xˉ而不是 x T \mathbf{x}_T xT表示。因为 x ˉ \bar{\mathbf{x}} xˉ是优化路径的平滑版本。只要知道 r , L r, L r,L和 T T T,我们就可以选择学习率 η = r / ( L T ) \eta = r/(L \sqrt{T}) η=r/(LT)。这个就是上界 r L / T rL/\sqrt{T} rL/T。也就是说,我们将按照速度 O ( 1 / T ) \mathcal{O}(1/\sqrt{T}) O(1/T)收敛到最优解。
随机梯度和有限样本
到目前为止,在谈论随机梯度下降时,我们进行得有点快而松散。我们假设从分布 p ( x , y ) p(x, y) p(x,y)中采样得到样本 x i x_i xi(通常带有标签 y i y_i yi),并且用它来以某种方式更新模型参数。特别是,对于有限的样本数量,我们仅仅讨论了由某些允许我们在其上执行随机梯度下降的函数 δ x i \delta_{x_i} δxi和 δ y i \delta_{y_i} δyi组成的离散分布 p ( x , y ) = 1 n ∑ i = 1 n δ x i ( x ) δ y i ( y ) p(x, y) = \frac{1}{n} \sum_{i=1}^n \delta_{x_i}(x) \delta_{y_i}(y) p(x,y)=n1∑i=1nδxi(x)δyi(y)。
但是,这不是我们真正做的。在本节的简单示例中,我们只是将噪声添加到其他非随机梯度上,也就是说,我们假装有成对的 ( x i , y i ) (x_i, y_i) (xi,yi)。事实证明,这种做法在这里是合理的(有关详细讨论,请参阅练习)。更麻烦的是,在以前的所有讨论中,我们显然没有这样做。相反,我们遍历了所有实例恰好一次。要了解为什么这更可取,可以反向考虑一下,即我们有替换地从离散分布中采样 n n n个观测值。随机选择一个元素 i i i的概率是 1 / n 1/n 1/n。因此选择它至少一次就是
P ( c h o o s e i ) = 1 − P ( o m i t i ) = 1 − ( 1 − 1 / n ) n ≈ 1 − e − 1 ≈ 0.63. P(\mathrm{choose~} i) = 1 - P(\mathrm{omit~} i) = 1 - (1-1/n)^n \approx 1-e^{-1} \approx 0.63. P(choose i)=1−P(omit i)=1−(1−1/n)n≈1−e−1≈0.63.
类似的推理表明,挑选一些样本(即训练示例)恰好一次的概率是
( n 1 ) 1 n ( 1 − 1 n ) n − 1 = n n − 1 ( 1 − 1 n ) n ≈ e − 1 ≈ 0.37. {n \choose 1} \frac{1}{n} \left(1-\frac{1}{n}\right)^{n-1} = \frac{n}{n-1} \left(1-\frac{1}{n}\right)^{n} \approx e^{-1} \approx 0.37. (1n)n1(1−n1)n−1=n−1n(1−n1)n≈e−1≈0.37.
这导致与无替换采样相比,方差增加并且数据效率降低。因此,在实践中我们执行后者(这是本书中的默认选择)。最后一点注意,重复采用训练数据集的时候,会以不同的随机顺序遍历它。
小结
- 对于凸问题,我们可以证明,对于广泛的学习率选择,随机梯度下降将收敛到最优解。
- 对于深度学习而言,情况通常并非如此。但是,对凸问题的分析使我们能够深入了解如何进行优化,即逐步降低学习率,尽管不是太快。
- 如果学习率太小或太大,就会出现问题。实际上,通常只有经过多次实验后才能找到合适的学习率。
- 当训练数据集中有更多样本时,计算梯度下降的每次迭代的代价更高,因此在这些情况下,首选随机梯度下降。
- 随机梯度下降的最优性保证在非凸情况下一般不可用,因为需要检查的局部最小值的数量可能是指数级的。
相关文章:

【深度学习笔记】优化算法——随机梯度下降
随机梯度下降 在前面的章节中,我们一直在训练过程中使用随机梯度下降,但没有解释它为什么起作用。为了澄清这一点,我们刚在 :numref:sec_gd中描述了梯度下降的基本原则。本节继续更详细地说明随机梯度下降(stochastic gradient d…...
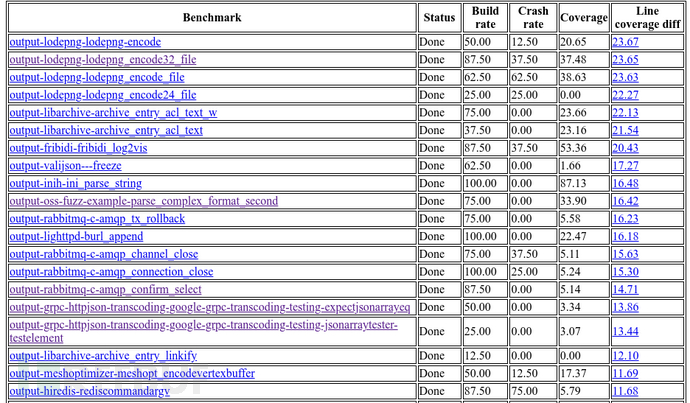
oss-fuzz-gen:一款基于LLM的模糊测试对象生成与评估框架
关于oss-fuzz-gen oss-fuzz-gen是一款基于LLM的模糊测试对象生成与评估框架,该工具可以帮助广大研究人员使用多种大语言模型(LLM)生成真实场景中的C/C项目以执行模糊测试。 该工具基于Google的OSS-Fuzz平台实现其功能,并对生成的…...

深度神经网络 基本知识 记录
资料:https://www.bilibili.com/video/BV1K94y1Z7wn/?spm_id_from333.337.search-card.all.click&vd_source14a476de9132ba6b2c3cbc2221750b99 计划:3~4天 杂 人工智能包括ML,ML包括DL机器学习需要人工大量参与,DL模拟人的…...
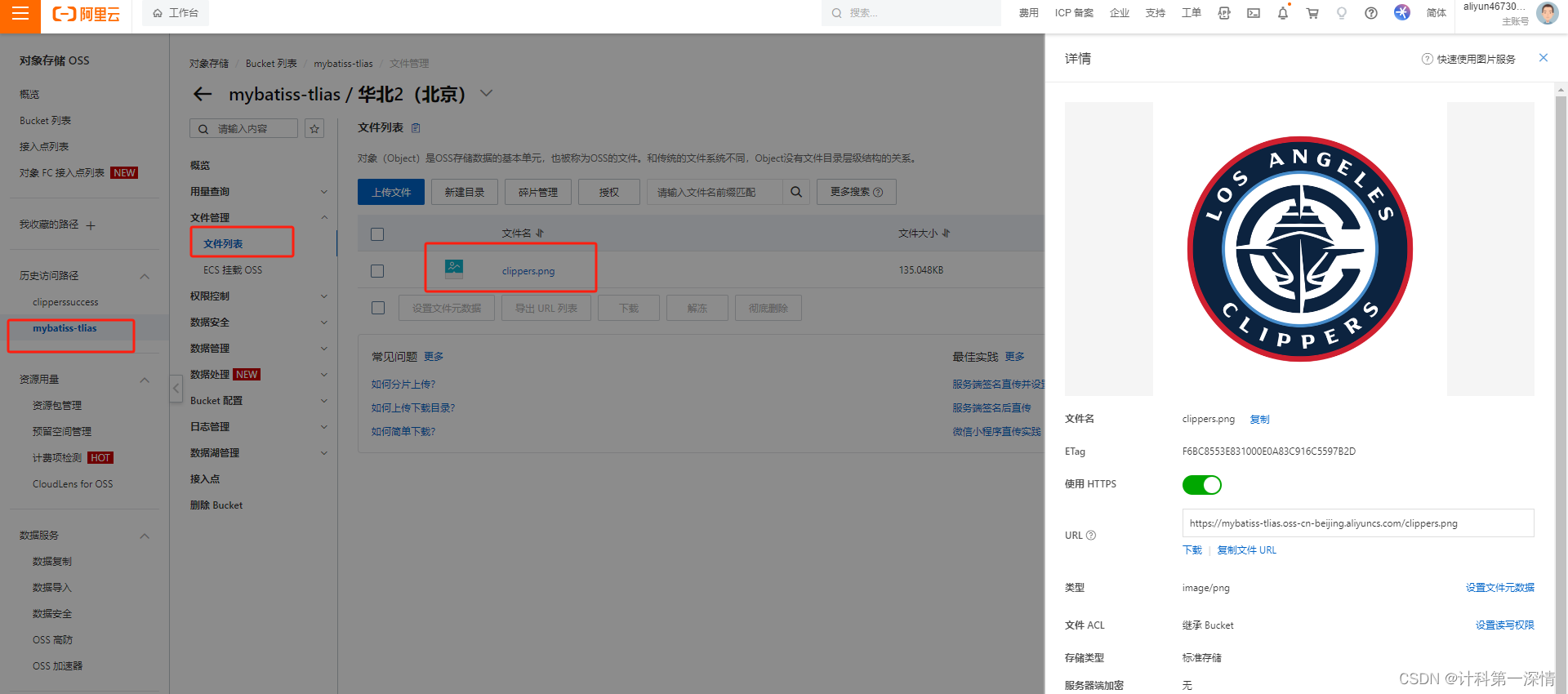
基于Springboot免费搭载轻量级阿里云OSS数据存储库(将本地文本、照片、视频、音频等上传云服务保存)
一、注册阿里云账户 打开https://www.aliyun.com/,申请阿里云账户并完成实名认证(个人)。这种情况就是完成了: 二、开通OSS服务 点击立即开通即可。 三、创建Bucket 申请id和secert: 进去创建一个Accesskey就会出现以…...
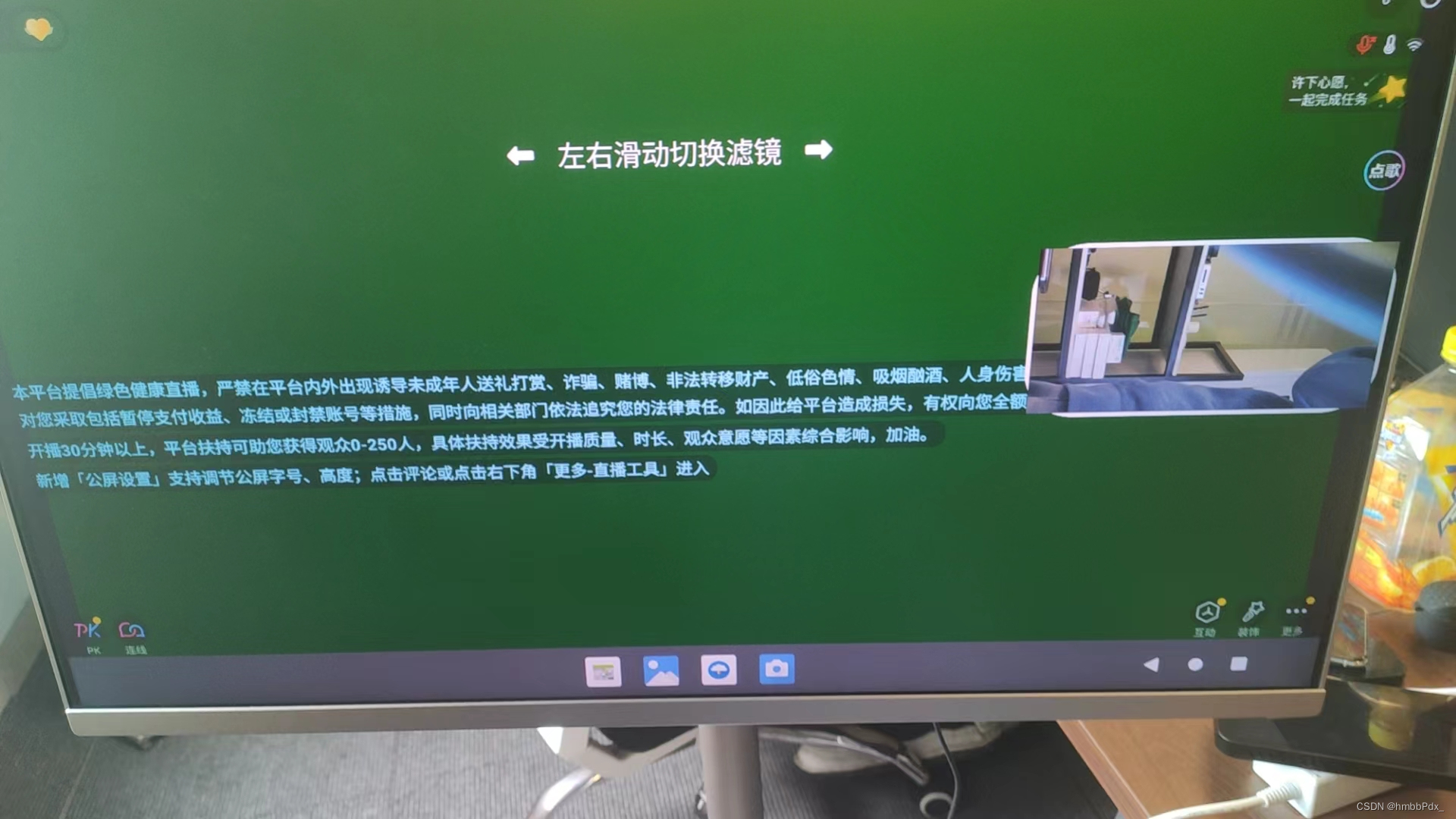
RK3568 Android12 适配抖音 各大APP
RK3568 Android12 适配抖音 各大APP SOC RK3568 system:Android 12 平台要适配抖音和各大APP 平台首先打开抖音发现摄像头预览尺寸不对只存在右上角,我将抖音APP装在手机上预览,发现是全屏 一开始浏览各大博客 给出的解决方法是修改framework 设置为全屏显示: framewo…...

[渗透教程]-022-内网穿透的高性能的反向代理应用
frp 简介 frp 是一个专注于内网穿透的高性能的反向代理应用,支持 TCP、UDP、HTTP、HTTPS 等多种协议。可以将内网服务以安全、便捷的方式通过具有公网 IP 节点的中转暴露到公网。 项目地址 https://github.com/fatedier/frp安装 linux 配置方式见如下链接🔗 frp安装配置…...

【计算机网络】深度学习HTTPS协议
💓 博客主页:从零开始的-CodeNinja之路 ⏩ 收录文章:【计算机网络】深度学习HTTPS协议 🎉欢迎大家点赞👍评论📝收藏⭐文章 目录 一:HTTPS是什么二:HTTPS的工作过程三:对称加密四:非对称加密五:中间人攻击1…...
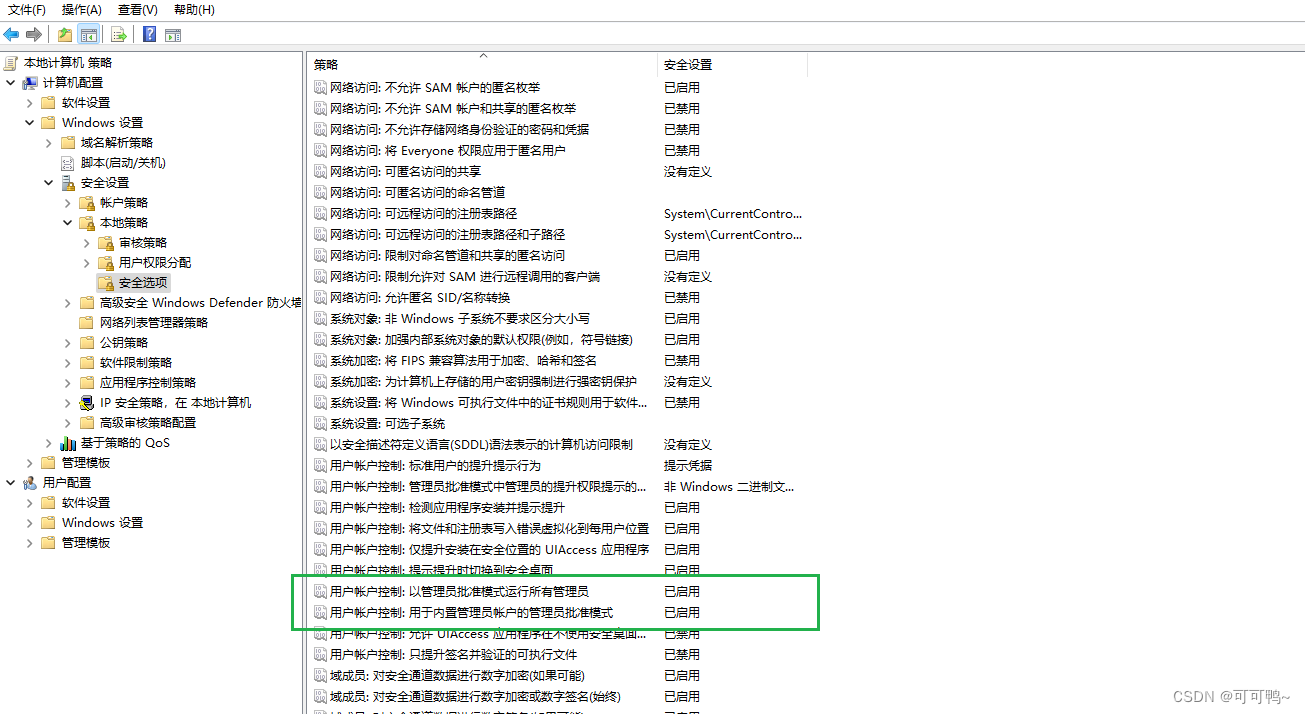
C盘新建的文件夹内需要管理员权限才能新建和删除解决问题记录
命令行输入命令gpedit.msc 如果执行成功那么直接看第二步 如果出现不存在此文件 那么用记事本将一以下代码粘贴进去,后缀命名为cmd。文件名无所谓,双击运行 echo offpushd "%~dp0"dir /b C:\Windows\servicing\Packages\Microsoft-Windows-Gr…...

2024年【道路运输企业安全生产管理人员】考试报名及道路运输企业安全生产管理人员免费试题
题库来源:安全生产模拟考试一点通公众号小程序 道路运输企业安全生产管理人员考试报名参考答案及道路运输企业安全生产管理人员考试试题解析是安全生产模拟考试一点通题库老师及道路运输企业安全生产管理人员操作证已考过的学员汇总,相对有效帮助道路运…...

四面体单元悬臂梁的Matlab有限元编程 | 实体单元 | Matlab源码 | 理论文本
专栏导读 作者简介:工学博士,高级工程师,专注于工业软件算法研究本文已收录于专栏:《有限元编程从入门到精通》本专栏旨在提供 1.以案例的形式讲解各类有限元问题的程序实现,并提供所有案例完整源码;2.单元…...

BurpSuite2024.2.1
1.更新介绍 此版本引入了特定的API 扫描功能,并将 Bambdas 合并到 Logger 捕获过滤器中。我们还改进了 DOM Invader 和 Burp Suite 导航记录器的功能,并进行了许多其他改进和错误修复。 API扫描 我们引入了特定的 API 扫描功能。您现在可以上传 OpenAP…...

【投稿优惠|火热征稿】2024年计算机技术与自动化发展国际会议 (ICCTAD 2024)
2024年计算机技术与自动化发展国际会议 (ICCTAD 2024) 2024 International Conference on Computer Technology and Automation Development (ICCTAD 2024) 【会议简介】 2024年计算机技术与自动化发展国际会议( ICCTAD 2024)将在中国武汉盛大开幕!这是一场在自动化…...
LeetCode.232. 用栈实现队列
题目 232. 用栈实现队列 分析 先了解一下栈和队列的特点: 栈:先进后出队列:先进先出 想用栈实现队列的特点,就需要使用两个栈。因为两个栈就可以将列表倒序。 假设第一个栈 s1 [1,2,3],第二个栈 s2 [] 。若循环…...
SpringBoot集成ElasticSearch(ES)
ElasticSearch环境搭建 采用docker-compose搭建,具体配置如下: version: 3# 网桥es -> 方便相互通讯 networks:es:services:elasticsearch:image: registry.cn-hangzhou.aliyuncs.com/zhengqing/elasticsearch:7.14.1 # 原镜像elasticsearch:7.…...
基于STC12C5A60S2系列1T 8051单片机的TM1638键盘数码管模块的数码管显示应用
基于STC12C5A60S2系列1T 8051单片机的TM1638键盘数码管模块的数码管显示应用 STC12C5A60S2系列1T 8051单片机管脚图STC12C5A60S2系列1T 8051单片机I/O口各种不同工作模式及配置STC12C5A60S2系列1T 8051单片机I/O口各种不同工作模式介绍TM1638键盘数码管模块概述TM1638键盘数码管…...

Qt插件之输入法插件的构建和使用(一)
文章目录 输入法概述输入法插件实现及调用输入键盘搭建定义样式自定义按钮实现自定义可拖动标签数字符号键盘候选显示控件滑动控件手绘输入控件输入法概述 常见的输入法有三种形式: 1.系统级输入法 2.普通程序输入法 3.程序自带的输入法 系统级输入法就是咱们通常意义上的输入…...

慢SQL调优-索引详解
Mysql 慢SQL调优-索引详解 前言一、慢查询日志设置二、explain查看执行计划三、索引失效四、索引操作五、profile 分析执行耗时 前言 最新的 Java 面试题,技术栈涉及 Java 基础、集合、多线程、Mysql、分布式、Spring全家桶、MyBatis、Dubbo、缓存、消息队列、Linu…...
知乎语音下载(mediadown)
知乎语音下载(mediadown) 一、介绍 知乎语音下载,能够帮助你下载知乎知学堂课程中的语音和视频。它不能帮你越过会员权限,下载你没权限访问的语音和视频。 二、下载地址 本站下载:知乎语音下载(mediadown) 百度网盘下载:知乎语音下载(mediadown) 三、安装教程 …...

2023 最新 IntelliJ IDEA 2023.3 详细配置步骤演示:新入职如何快速配置 IntelliJ IDEA?
博主猫头虎的技术世界 🌟 欢迎来到猫头虎的博客 — 探索技术的无限可能! 专栏链接: 🔗 精选专栏: 《面试题大全》 — 面试准备的宝典!《IDEA开发秘籍》 — 提升你的IDEA技能!《100天精通鸿蒙》 …...
Linux 下安装 Git
Linux 下安装 Git 1 参考2 安装2.1 通过 yum方式安装(不推荐)2.2 通过源码编译安装(推荐) 3 配置SSH 1 参考 Linux 下安装 Git 2 安装 2.1 通过 yum方式安装(不推荐) 在Linux上安装git仅需一行命令即可…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...
