第十四届蓝桥杯省赛真题 Java C 组【原卷】
文章目录
- 发现宝藏
- 【考生须知】
- 试题 A \mathrm{A} A : 求和
- 试题 B: 分糖果
- 试题 C: 三国游戏
- 试题 D : \mathrm{D}: D: 平均
- 试题 E \mathrm{E} E : 填充
- 试题 F : \mathrm{F}: F: 棋盘
- 试题 G: 子矩阵
- 试题 H: 公因数匹配
- 试题 I: 异或和之差
- 试题 J : \mathrm{J}: J: 太阳
发现宝藏
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。【宝藏入口】。
【考生须知】
考试开始后, 选手首先下载题目, 并使用考场现场公布的解压密码解压试题。
考试时间为 4 小时。考试期间选手可浏览自己已经提交的答案, 被浏览的答案允许拷贝。时间截止后,将无法继续提交或浏览答案。
对同一题目,选手可多次提交答案,以最后一次提交的答案为准。
选手必须通过浏览器方式提交自己的答案。选手在其它位置的作答或其它方式提交的答案无效。
试题包含 “结果填空” 和 “程序设计” 两种题型。
结果填空题:要求选手根据题目描述直接填写结果。求解方式不限。不要求源代码。把结果填空的答案直接通过网页提交即可, 不要书写多余的内容。
程序设计题:要求选手设计的程序对于给定的输入能给出正确的输出结果。考生的程序只有能运行出正确结果才有机会得分。
注意:在评卷时使用的输入数据与试卷中给出的示例数据可能是不同的。选手的程序必须是通用的, 不能只对试卷中给定的数据有效。
所有源码必须在同一文件中。调试通过后,拷贝提交。
注意: 不要使用 package 语句。
注意:选手代码的主类名必须为:Main, 否则会被判为无效代码。
注意: 如果程序中引用了类库, 在提交时必须将 import 语句与程序的其他部分同时提交。只允许使用 Java 自带的类库。
试题 A \mathrm{A} A : 求和
本题总分:5 分
【问题描述】
求 1 (含) 至 20230408 (含) 中每个数的和。
【答案提交】
这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。
试题 B: 分糖果
本题总分:5 分
【问题描述】
两种糖果分别有 9 个和 16 个, 要全部分给 7 个小朋友, 每个小朋友得到的糖果总数最少为 2 个最多为 5 个, 问有多少种不同的分法。
只要有其中一个小朋友在两种方案中分到的糖果不完全相同, 这两种方案就算作不同的方案。
【答案提交】
这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。
试题 C: 三国游戏
时间限制: 3.0 s 3.0 \mathrm{~s} 3.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 10 分
【问题描述】
小蓝正在玩一款游戏。游戏中魏蜀吴三个国家各自拥有一定数量的士兵 X , Y , Z X, Y, Z X,Y,Z (一开始可以认为都为 0 )。游戏有 n n n 个可能会发生的事件, 每个事件之间相互独立且最多只会发生一次, 当第 i i i 个事件发生时会分别让 X , Y , Z X, Y, Z X,Y,Z 增加 A i , B i , C i A_{i}, B_{i}, C_{i} Ai,Bi,Ci 。
当游戏结束时 (所有事件的发生与否已经确定), 如果 X , Y , Z X, Y, Z X,Y,Z 的其中一个大于另外两个之和, 我们认为其获胜。例如, 当 X > Y + Z X>Y+Z X>Y+Z 时, 我们认为魏国获胜。小蓝想知道游戏结束时如果有其中一个国家获胜, 最多发生了多少个事件?
如果不存在任何能让某国获胜的情况, 请输出 -1 。
【输入格式】
输入的第一行包含一个整数 n n n 。
第二行包含 n n n 个整数表示 A i A_{i} Ai, 相邻整数之间使用一个空格分隔。
第三行包含 n n n 个整数表示 B i B_{i} Bi, 相邻整数之间使用一个空格分隔。
第四行包含 n n n 个整数表示 C i C_{i} Ci, 相邻整数之间使用一个空格分隔。
【输出格式】
输出一行包含一个整数表示答案。
【样例输入】
3 \begin{array}{lll}3 \end{array} 3
1 2 2 \begin{array}{lll}1 & 2 & 2\end{array} 122
2 3 2 \begin{array}{lll}2 & 3 & 2\end{array} 232
1 0 7 \begin{array}{lll}1 & 0 & 7\end{array} 107
【样例输出】
2 \begin{array}{lll}2\end{array} 2
【样例说明】
发生两个事件时,有两种不同的情况会出现获胜方。
发生 1,2 事件时蜀国获胜。
发生 1,3 事件时吴国获胜。
【评测用例规模与约定】
对于 40 % 40 \% 40% 的评测用例, n ≤ 500 n \leq 500 n≤500;
对于 70 % 70 \% 70% 的评测用例, n ≤ 5000 n \leq 5000 n≤5000 ;
对于所有评测用例, 1 ≤ n ≤ 1 0 5 , 1 ≤ A i , B i , C i ≤ 1 0 9 1 \leq n \leq 10^{5}, 1 \leq A_{i}, B_{i}, C_{i} \leq 10^{9} 1≤n≤105,1≤Ai,Bi,Ci≤109 。
试题 D : \mathrm{D}: D: 平均
时间限制: 3.0 s 3.0 \mathrm{~s} 3.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分:10 分
【问题描述】
有一个长度为 n n n 的数组 ( n n n 是 10 的倍数), 每个数 a i a_{i} ai 都是区间 [ 0 , 9 ] [0,9] [0,9] 中的整数。小明发现数组里每种数出现的次数不太平均, 而更改第 i i i 个数的代价为 b i b_{i} bi, 他想更改若干个数的值使得这 10 种数出现的次数相等 (都等于 n 10 \frac{n}{10} 10n ), 请问代价和最少为多少。
【输入格式】
输入的第一行包含一个正整数 n n n 。
接下来 n n n 行, 第 i i i 行包含两个整数 a i , b i a_{i}, b_{i} ai,bi, 用一个空格分隔。
【输出格式】
输出一行包含一个正整数表示答案。
【样例输入】
10 1 1 1 2 1 3 2 4 2 5 2 6 3 7 3 8 3 9 4 10 \begin{array}{ll}10 \\ 1 & 1 \\ 1 & 2 \\ 1 & 3 \\ 2 & 4 \\ 2 & 5 \\ 2 & 6 \\ 3 & 7 \\ 3 & 8 \\ 3 & 9 \\ 4 & 10\end{array} 10111222333412345678910
【样例输出】
27 \begin{array}{lll}27\end{array} 27
【样例说明】
只更改第 1 , 2 , 4 , 5 , 7 , 8 1,2,4,5,7,8 1,2,4,5,7,8 个数, 需要花费代价 1 + 2 + 4 + 5 + 7 + 8 = 27 1+2+4+5+7+8=27 1+2+4+5+7+8=27 。
【评测用例规模与约定】
对于 20 % 20 \% 20% 的评测用例, n ≤ 1000 n \leq 1000 n≤1000;
对于所有评测用例, n ≤ 100000 , 0 < b i ≤ 2 × 1 0 5 n \leq 100000,0<b_{i} \leq 2 \times 10^{5} n≤100000,0<bi≤2×105 。
试题 E \mathrm{E} E : 填充
时间限制: 3.0 s 3.0 \mathrm{~s} 3.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分:15 分
【问题描述】
有一个长度为 n n n 的 01 串, 其中有一些位置标记为 ?, 这些位置上可以任意填充 0 或者 1 , 请问如何填充这些位置使得这个 01 串中出现互不重叠的 00 和 11 子串最多, 输出子串个数。
【输入格式】
输入一行包含一个字符串。
【输出格式】
输出一行包含一个整数表示答案。
【样例输入】
1110 ? 0 \begin{array}{llllll}1110?0\end{array} 1110?0
【样例输出】
2 \begin{array}{llllll}2\end{array} 2
【样例说明】
如果在问号处填 0 , 则最多出现一个 00 和一个 11: 111000 。
【评测用例规模与约定】
对于所有评测用例, 1 ≤ n ≤ 1000000 1 \leq n \leq 1000000 1≤n≤1000000 。
试题 F : \mathrm{F}: F: 棋盘
时间限制: 3.0 s 3.0 \mathrm{~s} 3.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分:15 分
【问题描述】
小蓝拥有 n × n n \times n n×n 大小的棋盘, 一开始棋盘上全都是白子。小蓝进行了 m m m 次操作, 每次操作会将棋盘上某个范围内的所有棋子的颜色取反 (也就是白色棋子变为黑色, 黑色棋子变为白色)。请输出所有操作做完后棋盘上每个棋子的颜色。
【输入格式】
输入的第一行包含两个整数 n , m n, m n,m, 用一个空格分隔, 表示棋盘大小与操作数。
接下来 m m m 行每行包含四个整数 x 1 , y 1 , x 2 , y 2 x_{1}, y_{1}, x_{2}, y_{2} x1,y1,x2,y2, 相邻整数之间使用一个空格分隔, 表示将在 x 1 x_{1} x1 至 x 2 x_{2} x2 行和 y 1 y_{1} y1 至 y 2 y_{2} y2 列中的棋子颜色取反。
【输出格式】
输出 n n n 行, 每行 n n n 个 0 或 1 表示该位置棋子的颜色。如果是白色则输出 0 , 否则输出 1 。
【样例输入】
3 3 \begin{array}{llll}3 &3 \end{array} 33
1 1 2 2 \begin{array}{llll}1 & 1 & 2 & 2\end{array} 1122
2 2 3 3 \begin{array}{llll}2 & 2 & 3 & 3\end{array} 2233
1 1 3 3 \begin{array}{llll}1 & 1 & 3 & 3\end{array} 1133
【样例输出】
001 \begin{array}{llll}001\end{array} 001
010 \begin{array}{llll}010\end{array} 010
100 \begin{array}{llll}100\end{array} 100
【评测用例规模与约定】
对于 30 % 30 \% 30% 的评测用例, n m ≤ 500 n m \leq 500 nm≤500;
对于所有评测用例, 1 ≤ n , m ≤ 2000 , 1 ≤ x 1 ≤ x 2 ≤ n , 1 ≤ y 1 ≤ y 2 ≤ m 1 \leq n, m \leq 2000,1 \leq x_{1} \leq x_{2} \leq n, 1 \leq y_{1} \leq y_{2} \leq m 1≤n,m≤2000,1≤x1≤x2≤n,1≤y1≤y2≤m 。
试题 G: 子矩阵
时间限制: 5.0s 内存限制: 512.0MB 本题总分: 20 分
【问题描述】
给定一个 n × m n \times m n×m ( n n n 行 m m m 列 ) ) ) 的矩阵。
设一个矩阵的价值为其所有数中的最大值和最小值的乘积。求给定矩阵的所有大小为 a × b a \times b a×b ( a a a 行 b b b 列 ) ) ) 的子矩阵的价值的和。
答案可能很大,你只需要输出答案对 998244353 取模后的结果。
【输入格式】
输入的第一行包含四个整数分别表示 n , m , a , b n, m, a, b n,m,a,b, 相邻整数之间使用一个空格分隔。
接下来 n n n 行每行包含 m m m 个整数, 相邻整数之间使用一个空格分隔, 表示矩阵中的每个数 A i , j A_{i, j} Ai,j 。
【输出格式】
输出一行包含一个整数表示答案。
【样例输入】
2 3 1 2 \begin{array}{llll}2 & 3 & 1 & 2\end{array} 2312
1 2 3 \begin{array}{lll}1 & 2 & 3\end{array} 123
4 5 6 \begin{array}{lll}4 & 5 & 6\end{array} 456
【样例输出】
58 \begin{array}{llllll}58\end{array} 58
【样例说明】
1 × 2 + 2 × 3 + 4 × 5 + 5 × 6 = 58 1 \times 2+2 \times 3+4 \times 5+5 \times 6=58 1×2+2×3+4×5+5×6=58 。
【评测用例规模与约定】
对于 40 % 40 \% 40% 的评测用例, 1 ≤ n , m ≤ 100 1 \leq n, m \leq 100 1≤n,m≤100 ;
对于 70 % 70 \% 70% 的评测用例, 1 ≤ n , m ≤ 500 1 \leq n, m \leq 500 1≤n,m≤500 ;
对于所有评测用例, 1 ≤ a ≤ n ≤ 10001 ≤ b ≤ m ≤ 10001 ≤ A i , j ≤ 1 0 9 1 \leq a \leq n \leq 10001 \leq b \leq m \leq 10001 \leq A_{i, j} \leq 10^{9} 1≤a≤n≤10001≤b≤m≤10001≤Ai,j≤109 。
试题 H: 公因数匹配
时间限制: 3.0 s 3.0 \mathrm{~s} 3.0 s 内存限制: 512.0MB 本题总分:20 分
【问题描述】
给定 n n n 个正整数 A i A_{i} Ai, 请找出两个数 i , j i, j i,j 使得 i < j i<j i<j 且 A i A_{i} Ai 和 A j A_{j} Aj 存在大于 1 的公因数。
如果存在多组 i , j i, j i,j, 请输出 i i i 最小的那组。如果仍然存在多组 i , j i, j i,j, 请输出 i i i最小的所有方案中 j j j 最小的那组。
【输入格式】
输入的第一行包含一个整数 n n n 。
第二行包含 n n n 个整数分别表示 A 1 A 2 ⋯ A n A_{1} A_{2} \cdots A_{n} A1A2⋯An, 相邻整数之间使用一个空格分隔。
【输出格式】
输出一行包含两个整数分别表示题目要求的 i , j i, j i,j, 用一个空格分隔。
【样例输入】
5 \begin{array}{lllll}5 \end{array} 5
5 3 2 6 9 \begin{array}{lllll}5 & 3 & 2 & 6 & 9\end{array} 53269
【样例输出】
2 4 \begin{array}{lllll}2 & 4\end{array} 24
【评测用例规模与约定】
对于 40 % 40 \% 40% 的评测用例, n ≤ 5000 n \leq 5000 n≤5000;
对于所有评测用例, 1 ≤ n ≤ 1 0 5 , 1 ≤ A i ≤ 1 0 6 1 \leq n \leq 10^{5}, 1 \leq A_{i} \leq 10^{6} 1≤n≤105,1≤Ai≤106 。
试题 I: 异或和之差
时间限制: 3.0 s 3.0 \mathrm{~s} 3.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分:25 分
【问题描述】
给定一个含有 n n n 个元素的数组 A i A_{i} Ai, 你可以选择两个不相交的子段。求出这两个子段内的数的异或和的差值的最大值。
【输入格式】
输入的第一行包含一个整数 n n n 。
第二行包含 n n n 个整数 A i A_{i} Ai, 相邻整数之间使用一个空格分隔。
【输出格式】
输出一行包含一个整数表示答案。
【样例输入】
6 \begin{array}{llllll}6 \end{array} 6
1 2 4 9 2 7 \begin{array}{llllll}1 & 2 & 4 & 9 & 2 & 7\end{array} 124927
【样例输出】
14 \begin{array}{llllll}14\end{array} 14
【样例说明】
两个子段可以分别选 1 和 4 , 9 , 2 4,9,2 4,9,2, 差值为 15 − 1 = 14 15-1=14 15−1=14 。
【评测用例规模与约定】
对于 40 % 40 \% 40% 的评测用例, n ≤ 5000 n \leq 5000 n≤5000;
对于所有评测用例, 2 ≤ n ≤ 2 × 1 0 5 , 0 ≤ A i ≤ 2 20 2 \leq n \leq 2 \times 10^{5}, 0 \leq A_{i} \leq 2^{20} 2≤n≤2×105,0≤Ai≤220 。
试题 J : \mathrm{J}: J: 太阳
时间限制: 3.0 s 3.0 \mathrm{~s} 3.0 s 内存限制: 512.0MB 本题总分:25 分
【问题描述】
这天,小蓝在二维坐标系的点 ( X , Y ) (X, Y) (X,Y) 上放了一个太阳, 看做点光源。
他拿来了 n n n 条线段, 将它们平行于 x x x 轴放置在了坐标系中, 第 i i i 条线段的左端点在 x i , y i x_{i}, y_{i} xi,yi, 长度为 l i l_{i} li 。线段之间不会有重合或部分重合的情况 (但可能出现端点相交)。小蓝想知道有多少条线段能被太阳照亮 (一条线段有长度大于 0 的部分被照亮就算)。
【输入格式】
输入的第一行包含三个正整数 n , X , Y n, X, Y n,X,Y, 相邻整数之间使用一个空格分隔。
接下来 n n n 行, 第 i i i 行包含三个整数 x i , y i , l i x_{i}, y_{i}, l_{i} xi,yi,li, 相邻整数之间使用一个空格分隔。
【输出格式】
输出一行包含一个正整数表示答案。
【样例输入】
3 10 2000000 \begin{array}{lll}3& 10& 2000000\end{array} 3102000000
5 3 5 \begin{array}{lll}5 & 3 & 5\end{array} 535
6 2 4 \begin{array}{lll}6 & 2 & 4\end{array} 624
0 110 \begin{array}{lll}0 & 110\end{array} 0110
【样例输出】
2 \begin{array}{lll}2\end{array} 2
【样例说明】
第一条线段在最上面被照亮, 第二条线段被第一条完全挡住, 第三条线段左边的一段能被照亮。
【评测用例规模与约定】
对于 30 % 30 \% 30% 的评测用例, n ≤ 1000 n \leq 1000 n≤1000 ;
对于所有评测用例, 1 ≤ n ≤ 100000 , 0 ≤ x i , X ≤ 1 0 7 , 0 < y i ≤ 1 0 5 , 0 < l i ≤ 1 \leq n \leq 100000,0 \leq x_{i}, X \leq 10^{7}, 0<y_{i} \leq 10^{5}, 0<l_{i} \leq 1≤n≤100000,0≤xi,X≤107,0<yi≤105,0<li≤ 100 , 1 0 6 < Y ≤ 1 0 7 100,10^{6}<Y \leq 10^{7} 100,106<Y≤107 。
相关文章:

第十四届蓝桥杯省赛真题 Java C 组【原卷】
文章目录 发现宝藏【考生须知】试题 A \mathrm{A} A : 求和试题 B: 分糖果试题 C: 三国游戏试题 D : \mathrm{D}: D: 平均试题 E \mathrm{E} E : 填充试题 F : \mathrm{F}: F: 棋盘试题 G: 子矩阵试题 H: 公因数匹配试题 I: 异或和之差试题 J : \mathrm{J}: J: 太阳 发现宝…...

v-model 粗略解析
v-model 粗略解析 v-model是什么? 双向数据绑定,可以从data流向页面,也可以从页面流向data通常用于表单收集,v-model 默认绑定 value 值书写形式: v-model:value"" 或 v-model v-model原理是什么…...

【vue elementUI】修改el-dropdown样式
实现效果如下: 代码如下: <el-dropdown trigger"click" command"handleCommand" active-text-color"#606266"><span class"product-card">{{getCategoryName(categoryId)}}</span><el-dro…...
6语言交易所/多语言交易所php源码/微盘PHP源码
6语言交易所PHP源码,简单测试了一下,功能基本都是正常的。 由于是在本地测试的运行环境的问题,K线接口有点问题,应该在正式环境下是OK的。 源码下载地址:6语言交易所/多语言交易所php源码/微盘PHP源码.zip 程序截图…...
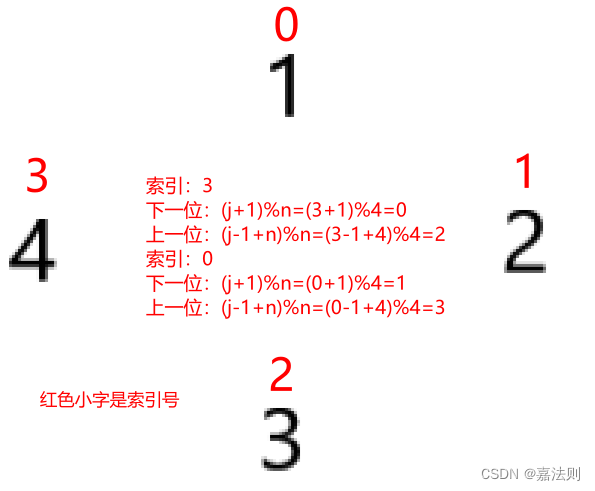
动态规划——传球问题
题目链接:1.传球游戏 - 蓝桥云课 (lanqiao.cn) 本题关键在于动态规划的数组设计,以及围坐一圈时索引的变化。 首先是动态规划,由于是求球传递m次回到第一位同学,那么就可以设计成一个二维数组,每个位置代表的是&#x…...

Spring: 文件服务使用spring.web.resources.static-locations配置实现文件预览功能
文章目录 一、spring.web.resources.static-locations配置实现文件预览功能1、来实现文件预览的步骤2、总结 二、其他的文件预览实现方式1、使用Controller处理文件预览请求2、集成第三方文件预览库3、使用专门的文件预览服务4、配置Nginx等反向代理进行文件预览5、注意事项&am…...

分享常用的62 个九宫格抽奖及各种宫格效果源码
九宫格抽奖及各种宫格效果详细介绍 功演示效果及源码下载地址:https://www.erdangjiade.com/js/17-0-0-0 九宫格抽奖盘是一种常见的抽奖形式,由九个格子组成,每个格子代表一个奖项。抽奖时,指针会随机旋转,最终落在某…...

【Stable Diffusion】入门-03:图生图基本步骤+参数解读
目录 1 图生图原理2 基本步骤2.1 导入图片2.2 书写提示词2.3 参数调整 3 随机种子的含义4 拓展应用 1 图生图原理 当提示词不足以表达你的想法,或者你希望以一个更为简单清晰的方式传递一些要求的时候,可以给AI输入一张图片,此时图片和文字是…...

数学建模-多目标规划算法(美赛建模)
💞💞 前言 hello hello~ ,这里是viperrrrrrr~💖💖 ,欢迎大家点赞🥳🥳关注💥💥收藏🌹🌹🌹 💥个人主页ÿ…...
安装、配置MySQL
安装相关软件 MySQL Server、MySQL Workbench MySQL Server:专门用来提供数据存储和服务的软件 MySQL Workbench:可视化的 MySQL 管理工具 官网安装 https://www.mysql.com/ 官网 MySQL :: Download MySQL Installer 安装包路径 在这里选择版本和和对应…...
)
C++面试100问(九)
C中typdef和#define区别? #define是预处理命令,在预处理是执行简单的替换,不做正确性的检查;typedef是在编译时处理的,它是在自己的作用域内给已经存在的类型一个别名。 C中有哪些调试程序的方法? windows…...

出海品牌必备指南:海外网红营销5大底层逻辑解析
随着全球化的推进,品牌出海已经成为许多企业拓展市场的重要策略之一。在这个过程中,海外网红营销成为品牌吸引目标受众、提升知名度的有效工具。然而,要在海外市场取得成功,并不仅仅是找准网红合作伙伴,更需要深入了解…...

Linux/Ubuntu/Debian的终端中和的区别
下边举例说明: “cd /home & wine ps.exe”和“cd /home && wine ps.exe”之间的区别在于命令在类 Unix shell 环境(例如 Linux 或 macOS)中执行的方式: ‘cd /home & wine ps.exe’: 在此命令中,“…...

docker compose部署opensearch集群
docker compose 配置 假设有两台电脑 A电脑的ip为192.168.1.100 B电脑的ip为192.168.1.103 A电脑的docker compose 配置 version: 3services:opensearch:image: opensearchproject/opensearch:2.1.0container_name: opensearch-node-1environment:- cluster.nameopensearch-c…...
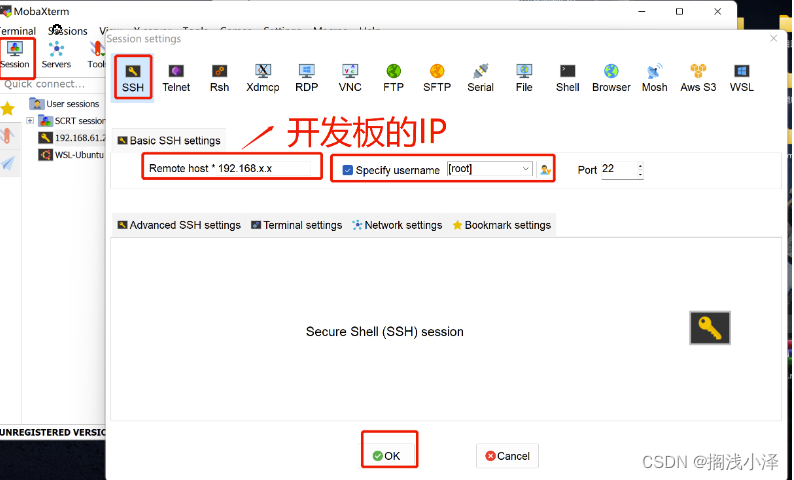
粤嵌6818开发板通过MobaXterm使用SSH连接开发板
链接:https://pan.baidu.com/s/18ISP4Ub1HtQx6jCvTQTUHw?pwdfjmu 提取码:fjmu 1.把SSH_config.tar.bz 下载到开发板中 2.解压 SSH_config.tar.bz 解压命令:tar -xzvf SSH_config.tar.bz 3.配置SSH 进入SSH/openssh目录&am…...

Python实战:Flask轻量级web框架入门
Flask是一个轻量级的Web框架,它是由Armin Ronacher开发的,使用Python语言编写。Flask易于上手,具有高度的可扩展性,非常适合快速开发Web应用程序。 一.Flask简介 Flask是一个基于Werkzeug WSGI工具箱和Jinja2模板引擎的Web框架。…...
docker 安装minio,详细图解
废话不多说,直接上干货 docker 安装minio 拉取镜像 docker pull minio/minio创建数据目录、配置目录 mkdir /opt/minio/data mkdir /opt/minio/config启动容器 docker run -p 9000:9000 -p 9090:9090 \--name minio \-d --restartalways \-e "MINIO_ACCESS_KE…...

【SpringBoot】请求与响应参数 IoC与DI 总结
文章目录 ① —— 请求 ——一、简单参数 RequestParam1.1 参数与形参 命名相同1.2 参数与形参 命名不同 二、实体参数2.1 简单实体对象2.2 复杂实体对象 三、数组集合参数3.1 数组3.2 集合 RequestParam 四、日期参数 DateTimeFormat五、JSON参数 RequestBody六、路径参数 Pat…...

100道面试必会算法-05-字符串转换整数 (atoi)
100道面试必会算法-05-字符串转换整数 (atoi) 实现一个 myAtoi(string s) 函数,使其能将字符串转换成一个 32 位有符号整数(类似 C/C 中的 atoi 函数)。 函数 myAtoi(string s) 的算法如下: 读入字符串并丢弃无用的前导空格检查…...
Ypay源支付2.8.8免授权聚合免签系统
本帖最后由 renleixiaoxu 于 2024-3-15 09:46 编辑 产品介绍 XPay是专为个人站长打造的聚合免签系统,拥有卓越的性能和丰富的功能。采用全新轻量化的界面UI,让您可以更加方便快捷地解决 知识付费和运营赞助的难题。同时,它基于高性能的Thin…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...

JavaScript 标签加载
目录 JavaScript 标签加载script 标签的 async 和 defer 属性,分别代表什么,有什么区别1. 普通 script 标签2. async 属性3. defer 属性4. type"module"5. 各种加载方式的对比6. 使用建议 JavaScript 标签加载 script 标签的 async 和 defer …...

安全领域新突破:可视化让隐患无处遁形
在安全领域,隐患就像暗处的 “幽灵”,随时可能引发严重事故。传统安全排查手段,常常难以将它们一网打尽。你是否好奇,究竟是什么神奇力量,能让这些潜藏的隐患无所遁形?没错,就是可视化技术。它如…...
