一文看懂softmax loss
文章目录
- softmax loss
- 1.softmax函数
- 2.交叉熵损失函数
- 3.softmax loss损失函数(重点)
- 4.带有temperature参数的softmax loss
- 参考
softmax loss
1.softmax函数
softmax函数是一种常用的激活函数,通常用于多分类任务中。给定一个向量,softmax函数将每个元素转化为一个介于0~1之间的概率值,并且所有元素的概率之和为1。softmax函数的定义如下:
softmax ( z ) i = e z i ∑ j = 1 K e z j \operatorname{softmax}(z)_i=\frac{e^{z_i}}{\sum_{j=1}^Ke^{z_j}} softmax(z)i=∑j=1Kezjezi
其中 z z z是输入向量, K K K是向量的维度。softmax函数的作用是将输入的原始分数(通常称之为logits1)转化为表示各个类别概率的分布。
2.交叉熵损失函数
交叉熵损失函数是用来衡量两个概率分布之间的差异性的一种度量方式。在深度学习中,常用交叉熵损失函数来衡量模型预测的概率分布与真实标签的分布之间的差异,从而作为优化目标来训练模型。
对于二分类问题,交叉熵损失函数的定义如下:
Binary Cross Entropy Loss = − 1 N ∑ i = 1 N [ y i log ( p i ) + ( 1 − y i ) log ( 1 − p i ) ] \text{Binary Cross Entropy Loss}=-\frac1N\sum_{i=1}^N\left[y_i\log(p_i)+(1-y_i)\log(1-p_i)\right] Binary Cross Entropy Loss=−N1i=1∑N[yilog(pi)+(1−yi)log(1−pi)]
其中 y i y_i yi是真实标签, p i p_i pi是模型预测的概率值, N N N是样本数。
对于多分类问题,交叉熵损失函数的定义如下:
Cross Entropy Loss = − 1 N ∑ i = 1 N ∑ k = 1 K y i , k log ( p i , k ) \text{Cross Entropy Loss}=-\frac1N\sum_{i=1}^N\sum_{k=1}^Ky_{i,k}\log(p_{i,k}) Cross Entropy Loss=−N1i=1∑Nk=1∑Kyi,klog(pi,k)
其中 y i , k y_{i,k} yi,k是第 i i i 个样本属于第 k k k 个类别的真实标签, p i , k p_{i,k} pi,k 是模型预测的第 i i i 个样本属于第 k k k 个类别的概率值, N N N 是样本数, K K K 是类别数。
3.softmax loss损失函数(重点)
softmax loss是深度学习中最常见的损失函数,完整的叫法为 Cross-entropy loss with softmax。softmax loss 由Fully Connected Layer,Softmax Function和Cross-entropy Loss组成。

softmax loss就是将softmax函数和交叉熵损失函数结合在了一起。
Softmax Loss = − 1 N ∑ i = 1 N ∑ k = 1 K y i , k log ( exp ( z i , k ) ∑ j = 1 K exp ( z i , j ) ) \text{Softmax Loss}=-\frac1N\sum_{i=1}^N\sum_{k=1}^Ky_{i,k}\log\left(\frac{\exp(z_{i,k})}{\sum_{j=1}^K\exp(z_{i,j})}\right) Softmax Loss=−N1i=1∑Nk=1∑Kyi,klog(∑j=1Kexp(zi,j)exp(zi,k))
其中 y i , k y_{i,k} yi,k 是第 i i i 个样本属于第 k k k 个类别的真实标签,当样本 i i i 属于类别 k k k 时, y i , k = 1 y_{i,k}=1 yi,k=1;否则, y i , k = 0 y_{i,k}=0 yi,k=0。 z i , k z_{i,k} zi,k 是样本 i i i 关于类别 k k k 的得分logits, N N N 是样本数, K K K 是类别数。
4.带有temperature参数的softmax loss
带有温度参数 T T T 的 softmax loss的损失函数如下:
Loss = − 1 N ∑ i = 1 N ∑ k = 1 K y i , k log ( exp ( z i , k / T ) ∑ j = 1 K exp ( z i , j / T ) ) \text{Loss}=-\frac1N\sum_{i=1}^N\sum_{k=1}^Ky_{i,k}\log\left(\frac{\exp(z_{i,k}/T)}{\sum_{j=1}^K\exp(z_{i,j}/T)}\right) Loss=−N1i=1∑Nk=1∑Kyi,klog(∑j=1Kexp(zi,j/T)exp(zi,k/T))
参考
1.Large-Margin Softmax Loss for Convolutional Neural Networks
2.Softmax Loss推导过程以及改进
3.深度学习中的温度参数(Temperature Parameter)是什么?
😃😃😃
logits就是一个向量,该向量下一步通常被输入到激活函数中,如softmax、sigmoid中。 ↩︎
相关文章:

一文看懂softmax loss
文章目录 softmax loss1.softmax函数2.交叉熵损失函数3.softmax loss损失函数(重点)4.带有temperature参数的softmax loss参考 softmax loss 1.softmax函数 softmax函数是一种常用的激活函数,通常用于多分类任务中。给定一个向量࿰…...

用C语言链表实现图书管理
#include <stdio.h> #include <stdlib.h> #include <string.h> struct ListNode {int val;//编号char title[50];//书名float price;//价格struct ListNode* next; };// 在尾部插入节点 struct ListNode* insertAtTail(struct ListNode* head, int val,char …...
Hello,Spider!入门第一个爬虫程序
在各大编程语言中,初学者要学会编写的第一个简单程序一般就是“Hello, World!”,即通过程序来在屏幕上输出一行“Hello, World!”这样的文字,在Python中,只需一行代码就可以做到。我们把这第一个爬虫就称之为“HelloSpider”&…...
AI实景无人自动直播间怎么搭建?三步教你轻松使用
最近很多朋友看到AI自动直播带货玩法,也想开启自己的自动直播间,但还是有些问题比较担心,这种自动讲解、自动回复做带货的直播间是不是很麻烦? 实景无人自动直播 实际上这种直播间搭建相当简单便捷!今天跟着笔者&…...
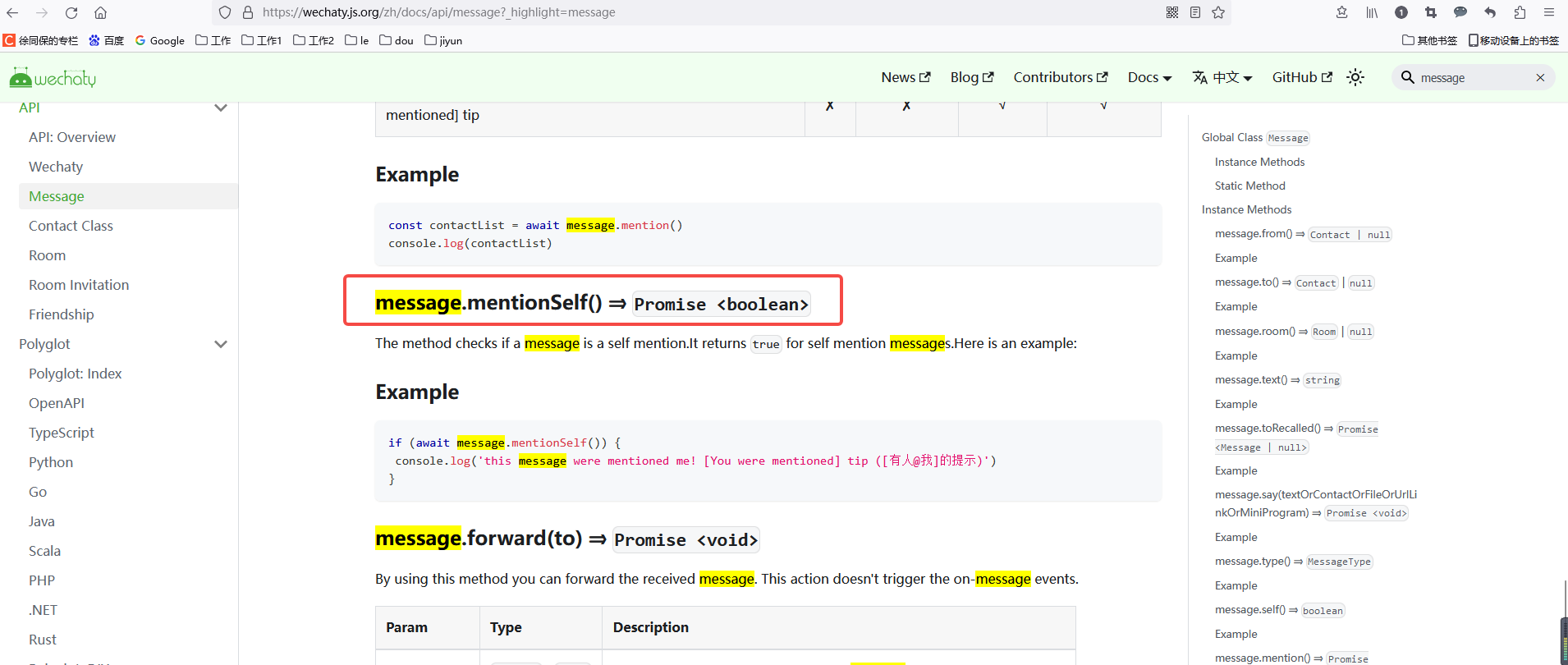
wechaty微信机器人,当机器人被@时做出响应
https://wechaty.js.org/zh/docs/api/message?_highlightmessage if (await msg.mentionSelf()) {console.log(this message were mentioned me! [You were mentioned] tip ([有人我]的提示))await room.say(不要微信机器人)} 我开发的人工智能学习网站: https://…...

8.6 Springboot项目实战 Spring Cache注解方式使用Redis
文章目录 前言一、配置Spring Cache1. @EnableCaching2. 配置CacheManager3. application.properties配置二、使用注解缓存数据1. 使用**@Cacheable** 改造查询代码2. 使用**@CacheEvict** 改造更新代码前言 在上文中我们使用Redis缓存热点数据时,使用的是手写代码的方式,这…...
rust引用本地crate
我们可以动态引用crate,build时从crate.io下载,但可能因无法下载导致build失败。首次正常引用三方crate,build时自动下载的crate源码,我们将其拷贝到固定目录中; build后可在RustRover中按住Ctrl键,在crat…...

分布式(计算机算法)
目录 分布式计算 分布式编辑 分布式和集群 分布式和集群的应用场景 分布式应用场景 集群应用场景 哪种技术更优、更快、更好呢 性能 稳定性 以下概念来源于百度百科 分布式计算 分布式计算是近年提出的一种新的计算方式。所谓分布式计算就是在两个或多个软件互相共享信息…...

CSS概念及入门
文章目录 1. CSS 概念及入门1.1. 简介1.2. 组成1.2.1. 选择器1.2.2. 属性 1.3. 区别 2. CSS 引入方式2.1. 行内样式2.1.1. 语法2.1.2. 特点 2.2. 内部样式2.2.1. 语法2.2.2. 特点 2.3. 外部样式2.3.1. 特点 2.4. 三种引入优先级 1. CSS 概念及入门 1.1. 简介 CSS 的全称为&am…...

用 C 语言模拟 Rust 的 Result 类型
在 Rust 中,Result<T, E> 类型是一个枚举,它表示一个操作可能成功并返回一个值 T,或者失败并返回一个错误 E。在 C 语言中,没有直接对应的 Result 类型,但我们可以使用结构体和枚举来模拟它。 下面是一个用 C 语…...
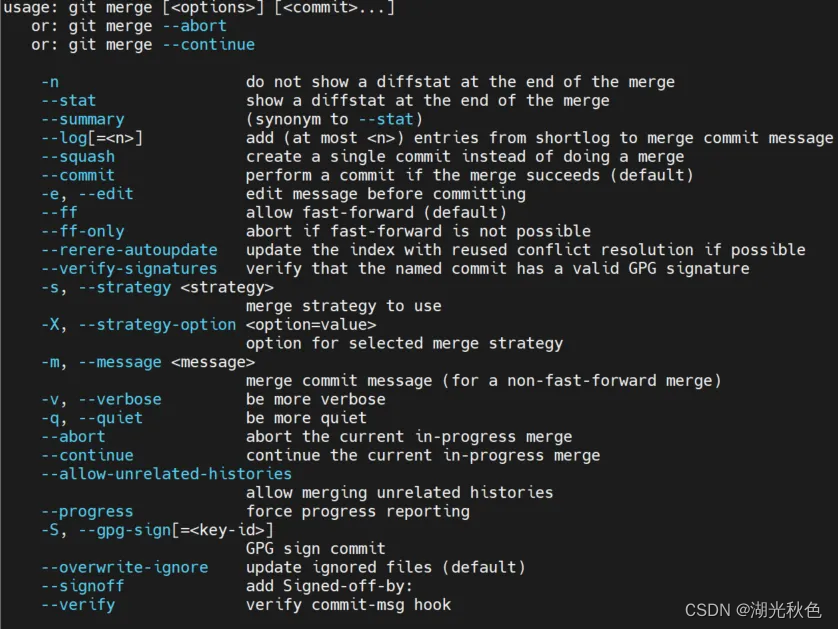
git基础命令(四)之分支命令
目录 基础概念git branch-r-a-v-vv-avv重命名分支删除分支git branch -h git checkout创建新的分支追踪远程分支同时切换到该分支创建新的分支并切换到该分支撤销对文件的修改,恢复到最近的提交状态:丢弃本地所有修改git checkout -h git merge合并指定分…...
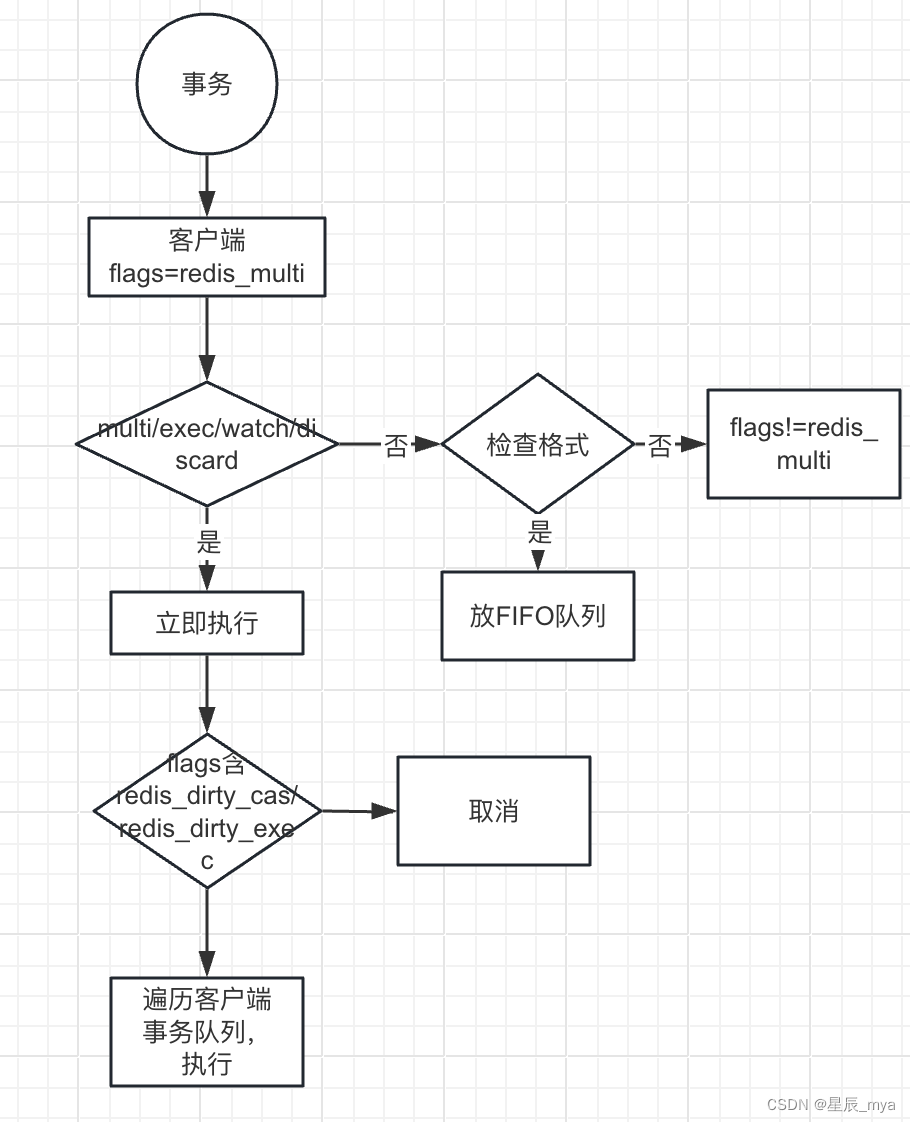
redis瘦身版
线程模型 纯内存操作/非阻塞io多路复用/单线程避免多线程频繁上下文切换 基于Reactor模式开发了网络事件处理器:文件事件处理器,单线程的 io多路监听多个socket,据socket事件类型选择对应的处理器,高性能网络通信模型,…...
使用ChatGPT高效完成简历制作[中篇]-有爱AI实战教程(五)
演示站点: https://ai.uaai.cn 对话模块 官方论坛: www.jingyuai.com 京娱AI 导读:在使用 ChatGPT 时,当你给的指令越精确,它的回答会越到位,举例来说,假如你要请它帮忙写文案,如果没…...
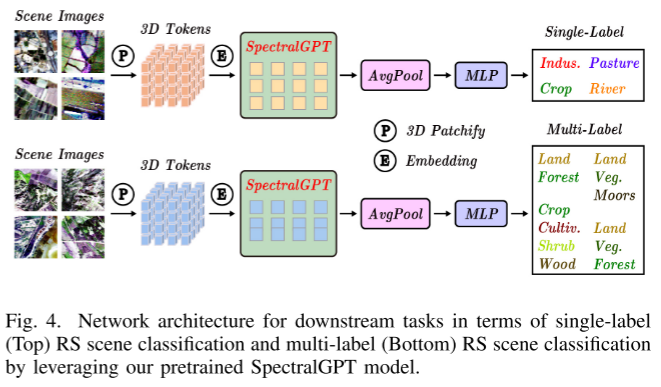
论文阅读——SpectralGPT
SpectralGPT: Spectral Foundation Model SpectralGPT的通用RS基础模型,该模型专门用于使用新型3D生成预训练Transformer(GPT)处理光谱RS图像。 重建损失由两个部分组成:令牌到令牌和频谱到频谱 下游任务:...

Redis的过期键是如何处理的?过期键的删除策略有哪些?请解释Redis的内存淘汰策略是什么?有哪些可选的淘汰策略?
Redis的过期键是如何处理的?过期键的删除策略有哪些? Redis的过期键处理是一个重要的内存管理机制,它确保在键过期后能够释放相应的内存空间。Redis对过期键的处理主要依赖于其删除策略,这些策略包括被动删除(惰性删除…...

软件测试方法 -- 等价类边界值
测试用例的定义 测试用例是为了特定的目的而设计的一组测试输入、执行条件和预期的结果,以便测试是否满足某个特定需求。通过大量的测试用例来检验软件的运行效果,他是指导测试工作进行的依据。 下面我们介绍几种常用的黑盒测试方法 等价类划分法 定…...

LeetCode——贪心算法(Java)
贪心算法 简介[简单] 455. 分发饼干[中等] 376. 摆动序列[中等] 53. 最大子数组和[中等] 122. 买卖股票的最佳时机 II[中等] 55. 跳跃游戏 简介 记录一下自己刷题的历程以及代码。写题过程中参考了 代码随想录的刷题路线。会附上一些个人的思路,如果有错误…...
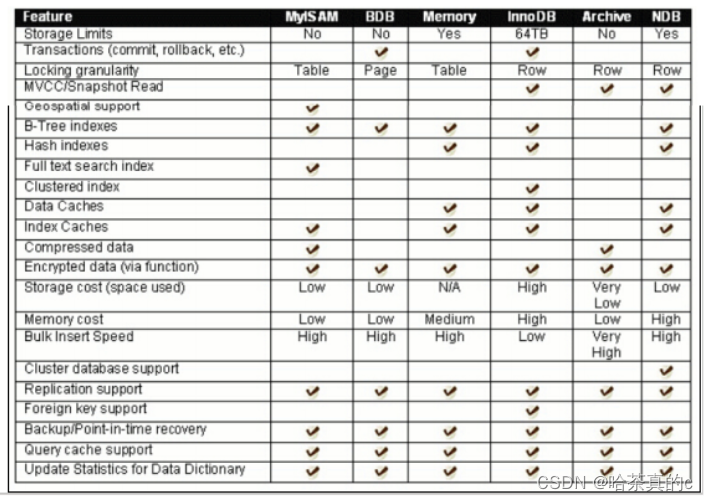
【MySQL】2. 数据库基础
1. 数据库基础(重点) 1.1 什么是数据库 存储数据用文件就可以了,为什么还要弄个数据库? 文件保存数据有以下几个缺点: 文件的安全性问题 文件不利于数据查询和管理 文件不利于存储海量数据 文件在程序中控制不方便 数据库存储介…...

《如何使用C语言去下三子棋?》
目录 一、环境配置 二、功能模块 1.打印菜单 2.初始化并打印棋盘 3、行棋 3.1玩家行棋 3.2电脑行棋 4、判断是否和棋 5.判赢 三、代码实现 1、test.c文件 2、game.c文件 3、game.h文件 一、环境配置 本游戏用到三个文件,分别是两个源文件test.c game.c 和…...
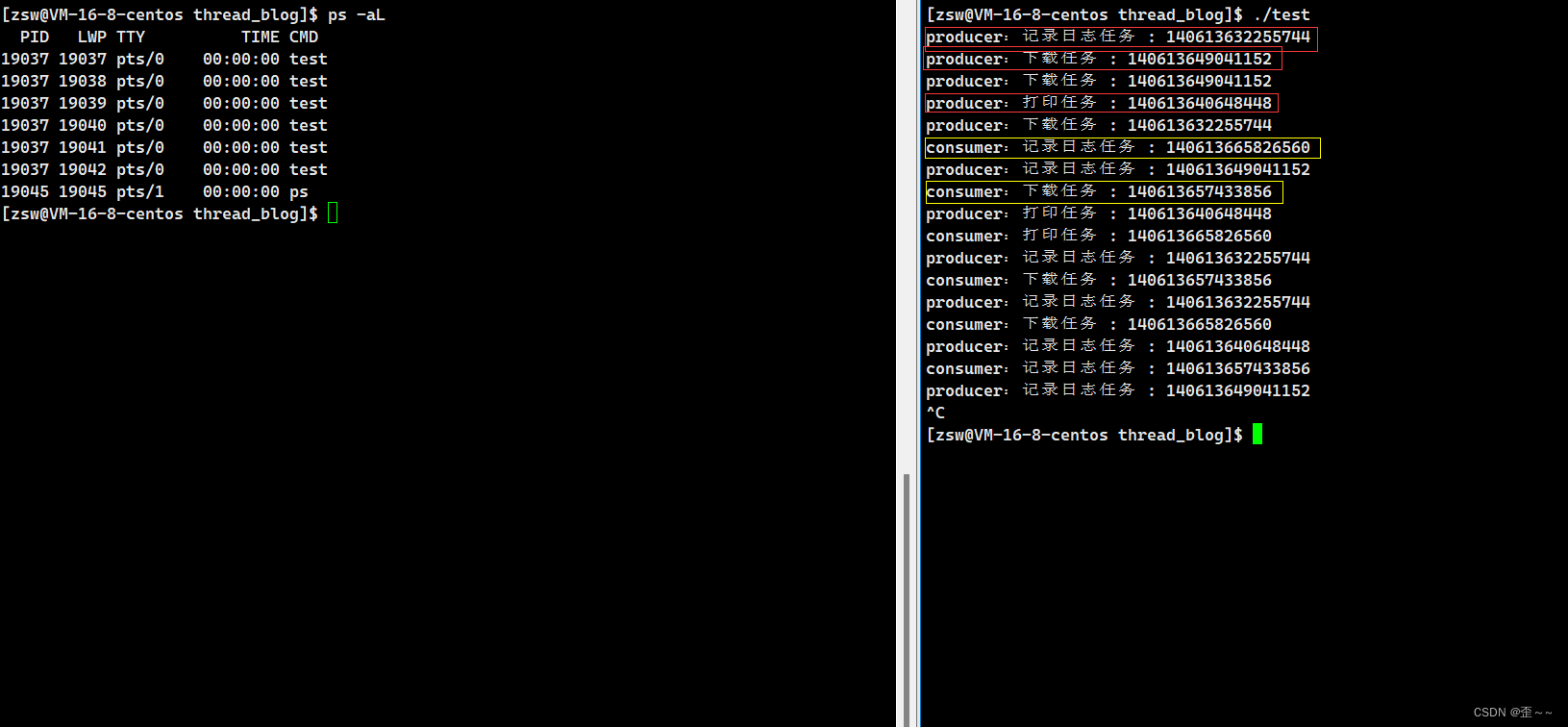
Linux——线程(4)
在上一篇博客中,我讲述了在多执行流并发访问共享资源的情况下,如何 使用互斥的方式来保证线程的安全性,并且介绍了Linux中的互斥使用的是 互斥锁来实现互斥功能,以及它的原理,在文章的结尾我提出了一个问题 用来引出同…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
