Unity中的网格创建和曲线变形
Unity中的网格创建和曲线变形
- 3D贝塞尔曲线变形
- 贝塞尔曲线基础
- 线性公式
- 二次方公式
- 三次方公式
- Unity 实现3D贝塞尔曲线变形
- 准备工作
- 脚本概述
- 变量定义
- 变量解析
- 函数解析 获取所有子节点
- GetAllChildren 获取所有子节点
- UpdateBezierBend 控制点更新
- CalculateBezier Bezier 曲线公式
- GetBendNormalVector 获取指定点上的法线向量偏移
- UpdateControlPoint 更新控制点的旋转角度
- CalculateBezierTangent 曲线求导(切线向量)
- BesselCurveDeformation_ZH 完整代码
- 自定义网格创建
- GridCreation_ZH 完整代码
- GridCreation_ZH 搭载
- 自定义网格创建 运行效果
- 网格创建和曲线变形 运行情况
在本篇博客中,我们将探讨如何使用Unity实现3D贝塞尔曲线变形效果。
3D贝塞尔曲线变形
贝塞尔曲线是一种常用的数学曲线,通过控制点和曲线影响力物体我们可以实现对网格的弯曲和变形。
在示例代码中,我们可以看到通过设置控制点数组、曲线影响力物体和控制物体曲线施加力等变量。
实现了对网格进行贝塞尔曲线变形的效果。这种技术在游戏中常用于创建动态的形变效果。
如弯曲的绳索、变形的角色模型等。
贝塞尔曲线基础
贝塞尔曲线是一种由控制点定义的数学曲线。
在3D空间中,我们通常使用3次贝塞尔曲线,它由四个控制点(起始点、两个中间点和结束点)组成。
贝塞尔曲线的形状受控制点的位置和权重影响。
控制点的位置决定了曲线经过的路径,而权重控制了曲线在控制点之间的弯曲程度。
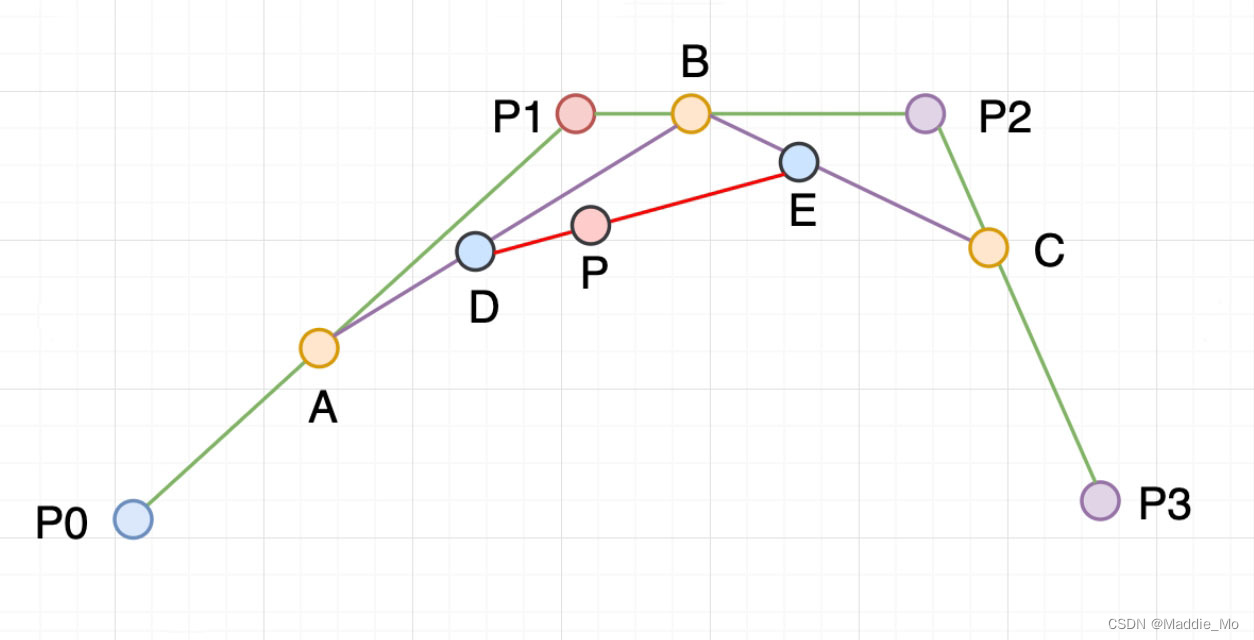
线性公式
给定点P0、P1,线性贝兹曲线只是一条两点之间的直线。
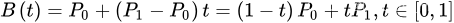
二次方公式
二次方贝兹曲线的路径由给定点P0、P1、P2的函数B(t)追踪:
TrueType字型就运用了以贝兹样条组成的二次贝兹曲线。
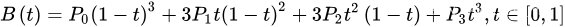
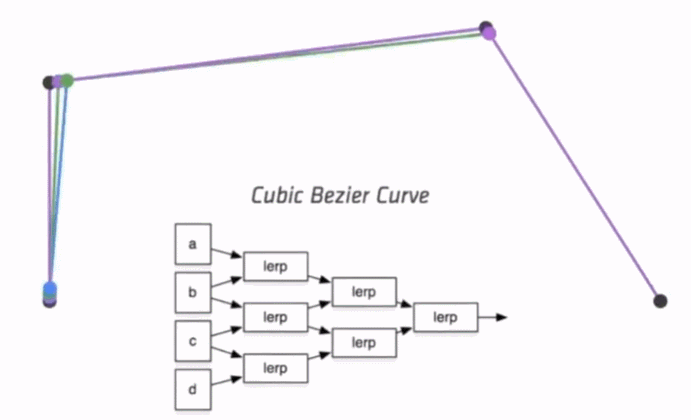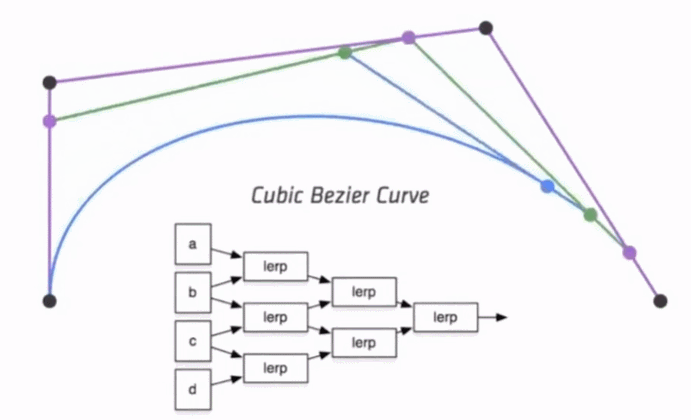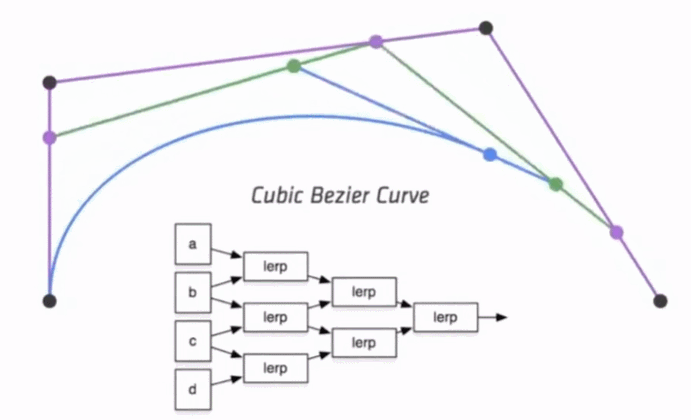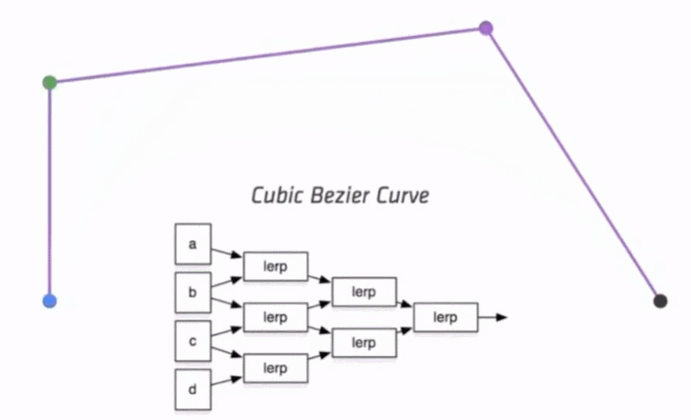
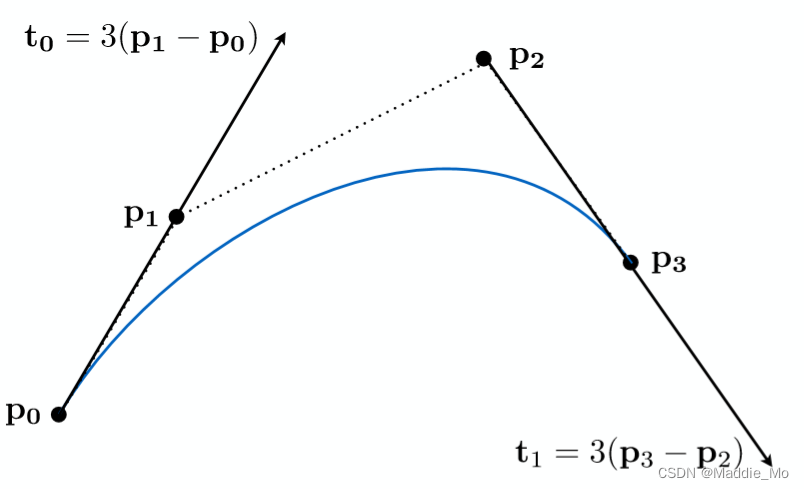
三次方公式
P0、P1、P2、P3四个点在平面或在三维空间中定义了三次方贝兹曲线。
曲线起始于P0走向P1,并从P2的方向来到P3。一般不会经过P1或P2。
这两个点只是在那里提供方向资讯。P0和P1之间的间距,决定了曲线在转而趋进P3之前
走向P2方向的“长度有多长”。
曲线的参数形式为:
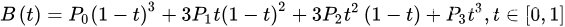
现代的成象系统,如PostScript、Asymptote和Metafont
运用了以贝兹样条组成的三次贝兹曲线,用来描绘曲线轮廓。
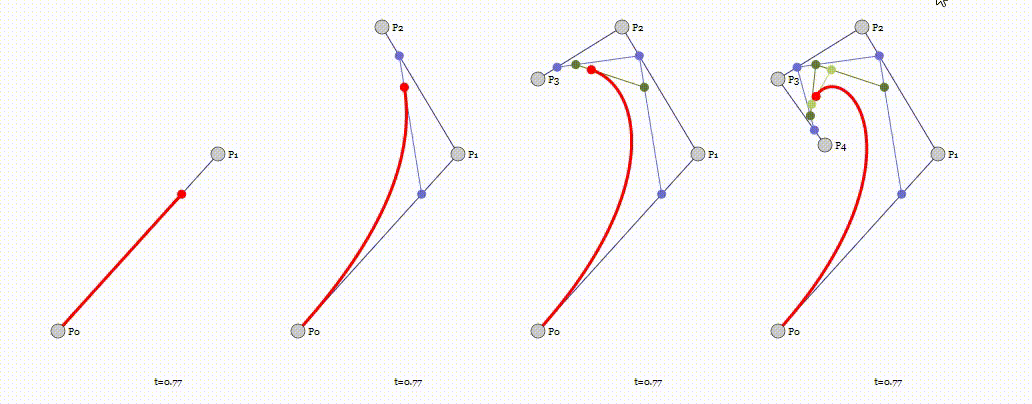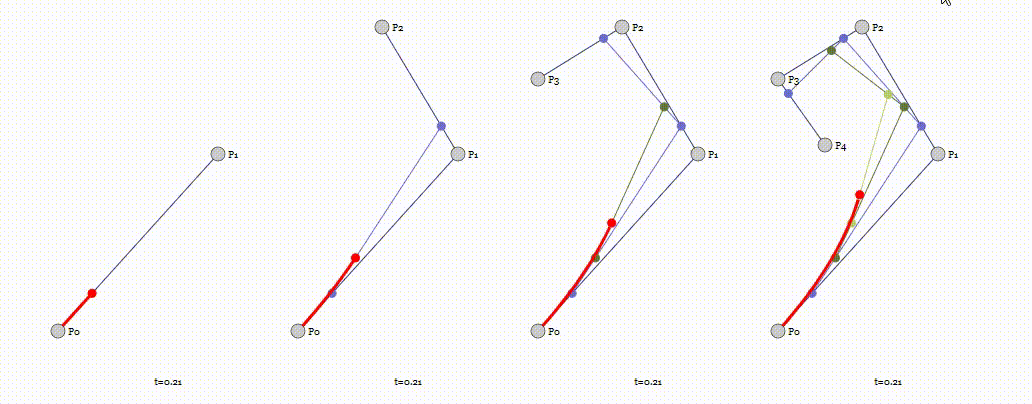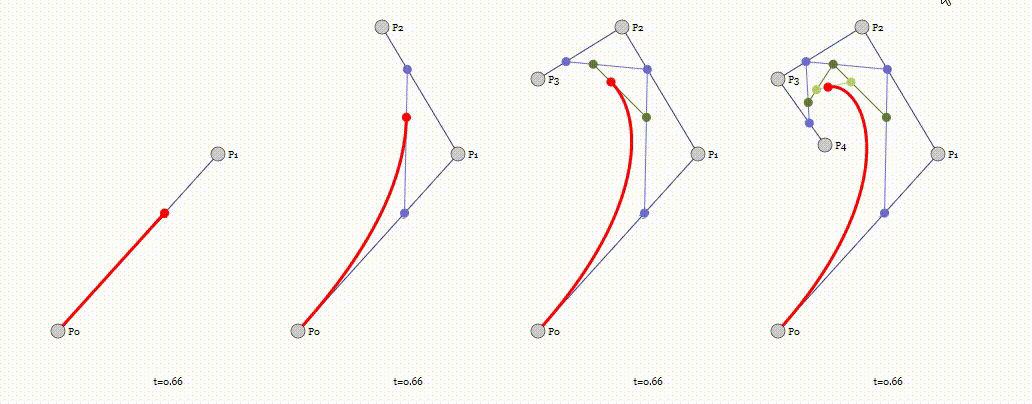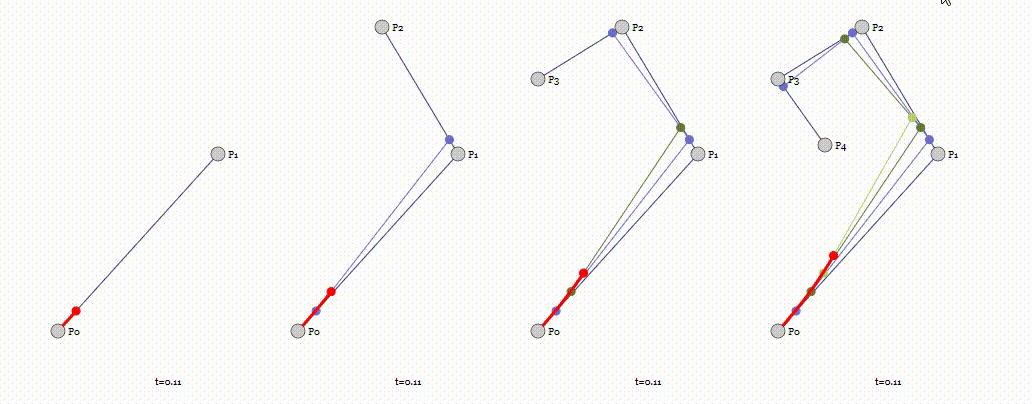
Unity 实现3D贝塞尔曲线变形
准备工作
首先,我们需要在Unity中创建一个空的GameObject,并将该脚本附加到该GameObject上。
接下来,我们需要创建一个网格,可以通过导入一个3D模型或者使用Unity内置的网格创建工具来完成。
脚本概述
让我们先来看一下脚本的整体结构:1.变量定义2.Start()函数2.Update()函数3.初始化函数4.获取所有子节点函数5.贝塞尔曲线Mesh计算相关函数
变量定义
[Header("存储贝塞尔曲线控制点数组")]public List<Transform> _CpArr;[Header("曲线影响力物体")]public Transform _ForceItem;[Range(0, 100f)][Header("控制物体曲线施加力")]public float _Force = 10;[Header("原始顶点位置")]private Vector3[] _OriVertices;[Header("网格数据")]private Mesh _Mesh;[Header("最后一个控制点位置")]//最后一个控制点的位置。用来计算mesh高度来计算tprivate Vector3 _TopPos;
变量解析
_CpArr: 存储贝塞尔曲线控制点数组的列表。
_ForceItem: 曲线影响力物体的Transform组件。
_Force: 控制物体曲线施加力的大小,范围在0到100之间。
_OriVertices: 原始顶点位置的数组。
_Mesh: 网格数据的Mesh组件。
_TopPos: 最后一个控制点的位置,用于计算mesh高度来计算t。
函数解析 获取所有子节点
Start(): 在脚本启动时调用,用于初始化操作。
Update(): 在每一帧更新时调用,用于更新控制点和网格。
Initialize(): 初始化函数,用于设置控制点数组和作用力变量等。
GetAllChildren 获取所有子节点
GetAllChildren: 获取所有子节点的函数,用于递归收集父节点下的所有子节点。
/// <summary>/// 获取所有子节点/// </summary>/// <param 父节点="_Parent"></param>/// <returns></returns>private List<Transform> GetAllChildren(Transform _Parent){List<Transform> _ListTra = new List<Transform>();foreach (Transform _Child in _Parent){//添加直接子节点_ListTra.Add(_Child);//递归收集后代节点List<Transform> _Descendants = GetAllChildren(_Child);_ListTra.AddRange(_Descendants);}return _ListTra;}
UpdateBezierBend 控制点更新
UpdateBezierBend: 控制点更新函数,根据施加在曲线上的力,计算并更新控制点的旋转角度。
/// <summary>/// 控制点更新/// 根据施加在曲线上的力,计算并更新控制点的旋转角度/// </summary>private void UpdateBezierBend(){//曲线弯曲方向Vector3 _BendVector = new Vector3(0, 0, 0);//弯曲布尔 true 无弯曲 false 弯曲bool _IsVertical = true;for (int i = 1; i < _CpArr.Count; i++){//对于每个控制点,将其位置转换为第一个控制点 _CpArr[0] 的局部空间Vector3 _Pos = _CpArr[i].TransformPoint(new Vector3(0, 0, 0));_Pos = _CpArr[0].InverseTransformPoint(_Pos);//判断当前控制点 x z 是否在非零//如果非零 就证明曲线在一个非垂直方向上弯曲if (IsEqualZero(_Pos.x) == false || IsEqualZero(_Pos.z) == false){//临时弯曲变量存储_BendVector.x = _Pos.x;_BendVector.z = _Pos.z;//弯曲布尔_IsVertical = false;break;}}//原始网格顶点数组Vector3[] _Temp = (Vector3[])_Mesh.vertices.Clone();//遍历所有顶点for (int i = 0; i < _OriVertices.Length; i++){//获取顶点坐标,计算t值Vector3 _OriPos = _OriVertices[i];Vector3 _BendPos;//没有弯曲if (_IsVertical == true){//当前顶点位置不变_BendPos = _OriPos;}//发生弯曲else{//将顶点的原始位置 _OriPos 的 y 分量除以顶部控制点 _TopPos 的 y 分量,计算参数 _CurvePositionfloat _T = _OriPos.y / _TopPos.y;//获取顶点在贝塞尔曲线上对应的坐标Vector3 _BezierPos = CalculateBezier(_T);//获取顶点在曲线上应有的法线偏移向量Vector3 _NormalVector = GetBendNormalVector(_T, _OriPos, _BendVector);//获取顶点在曲线上应有的垂直偏移向量Vector3 _VerticalVector = new Vector3(_OriPos.x, 0, _OriPos.z) - Vector3.Project(new Vector3(_OriPos.x, 0, _OriPos.z), _BendVector);//获取顶点最终弯曲位置_BendPos = _BezierPos + _NormalVector + _VerticalVector;}//转换回 mesh 本地坐标系_BendPos = _CpArr[0].TransformPoint(_BendPos);_BendPos = transform.InverseTransformPoint(_BendPos);_Temp[i] = _BendPos;}_Mesh.vertices = _Temp;}
CalculateBezier Bezier 曲线公式
CalculateBezier: Bezier曲线公式计算函数,根据给定的t值计算贝塞尔曲线上的点坐标。
/// <summary>/// Bezier 曲线公式/// 计算贝塞尔曲线上给定参数值 _CurvePosition 对应的位置/// </summary>/// <param 曲线位置="_CurvePosition"></param>/// <returns></returns>private Vector3 CalculateBezier(float _CurvePosition){//存储坐标Vector3 _Ret = new Vector3(0, 0, 0);//控制点数量int _Number = _CpArr.Count - 1;for (int i = 0; i <= _Number; i++){//获取第 i 个控制点的世界坐标,通过将其位置从控制点的局部坐标系转换到世界坐标Vector3 _Pi = _CpArr[i].TransformPoint(new Vector3(0, 0, 0));//将转换后的世界坐标再次转换回第一个控制点的局部坐标系,用于与其他控制点进行计算_Pi = _CpArr[0].InverseTransformPoint(_Pi);//根据贝塞尔曲线的定义,计算贝塞尔基函数的乘积项,并与控制点的局部坐标相乘//Cn_m(_Number, i) 是组合数函数 表示从 _Number 个控制点中选择 i 个的组合数_Ret = _Ret + Mathf.Pow(1 - _CurvePosition, _Number - i) * Mathf.Pow(_CurvePosition, i) * Cn_m(_Number, i) * _Pi;}return _Ret;}
GetBendNormalVector 获取指定点上的法线向量偏移
GetBendNormalVector: 获取顶点在曲线上应有的法线偏移向量的函数。
/// <summary>/// 获取指定点上的法线向量偏移/// 计算在贝塞尔曲线上给定参数值 _CurvePosition 对应位置的弯曲法向量/// </summary>/// <param 曲线位置="_CurvePosition"></param>/// <param 原始位置="_OriPos"></param>/// <param 弯曲方向="_BendVector"></param>/// <returns></returns>private Vector3 GetBendNormalVector(float _CurvePosition, Vector3 _OriPos, Vector3 _BendVector){//切线斜率Vector3 _TangentVector = CalculateBezierTangent(_CurvePosition);//切线竖直时,顶点在在弯曲向量上的投影向量即为法线向量if (IsEqualZero(_TangentVector.x) == true && IsEqualZero(_TangentVector.z) == true){//直接返回 原始位置 _OriPos 投影到弯曲向量 _BendVector 上的向量,作为法线向量return Vector3.Project(new Vector3(_OriPos.x, 0, _OriPos.z), _BendVector);}//存储计算得到的法线向量Vector3 _NormalVector = new Vector3(0, 0, 0);//计算切线向量与原始位置向量的点乘float _DirectFlag = Vector3.Dot(_BendVector, _OriPos);//判断法线向量朝向(法线向量有两个方向)//大于零 顶点坐标与弯曲方向同向if (_DirectFlag > 0){//切线水平,法线向量竖直向下if (IsEqualZero(_TangentVector.y) == true){_NormalVector.y = -1;}else{//切线朝上,法线向量与切线水平同向if (_TangentVector.y > 0){_NormalVector.x = _TangentVector.x;_NormalVector.z = _TangentVector.z;}//切线朝下,法线向量与切线水平反向else{_NormalVector.x = -_TangentVector.x;_NormalVector.z = -_TangentVector.z;}//使法线向量与切线向量水平且垂直于切线向量_NormalVector.y = -(_TangentVector.x * _NormalVector.x + _TangentVector.z * _NormalVector.z) / _TangentVector.y;}}//小于零 顶点坐标与弯曲方向反向else{//切线水平,法线向量竖直向上if (IsEqualZero(_TangentVector.y) == true){_NormalVector.y = 1;}else{//切线朝上,法线向量与切线水平反向if (_TangentVector.y > 0){_NormalVector.x = -_TangentVector.x;_NormalVector.z = -_TangentVector.z;}//切线朝下,法线向量与切线水平同向else{_NormalVector.x = _TangentVector.x;_NormalVector.z = _TangentVector.z;}//使得法线向量与切线向量水平且垂直于切线向量_NormalVector.y = -(_TangentVector.x * _NormalVector.x + _TangentVector.z * _NormalVector.z) / _TangentVector.y;}}//计算法线向量的模//法线向量的模应为到投影到弯曲面后,到中心点的距离float _Magnitude = Vector3.Project(new Vector3(_OriPos.x, 0, _OriPos.z), _BendVector).magnitude;//将法线向量按照该模进行缩放,使其长度与距离一致_NormalVector = _NormalVector.normalized * _Magnitude;//返回法线向量return _NormalVector;}
UpdateControlPoint 更新控制点的旋转角度
UpdateControlPoint: 控制点更新函数,根据施加在曲线上的力,计算并更新控制点的位置。
/// <summary>/// 更新控制点的旋转角度/// 根据受力计算各个控制点的旋转角度/// </summary>private void UpdateControlPoint(){//受力强度float _HandleForce = _Force;//根据受力计算各个控制点旋转角度for (int i = 1; i <= _CpArr.Count - 2; i++){//计算最大弯曲方向Vector3 _ForcePos = _ForceItem.transform.TransformPoint(new Vector3(0, 0, 0));_ForcePos = _CpArr[i - 1].InverseTransformPoint(_ForcePos);//计算从控制点到受力位置的向量Vector3 _ToVector = _ForcePos - _CpArr[i].localPosition;//得到该控制点的旋转角度Quaternion _MaxRotation = Quaternion.FromToRotation(Vector3.up, _ToVector);//获取控制点组件ControlPoint_ZH _Cp = _CpArr[i].gameObject.GetComponent<ControlPoint_ZH>();//计算弯曲比例 float _RotateRate = Mathf.Clamp(_HandleForce / _Cp._BendForce, 0f, 1.0f);//设置旋转角度_CpArr[i].localRotation = Quaternion.Lerp(Quaternion.Euler(0, 0, 0), _MaxRotation, _RotateRate);}}
CalculateBezierTangent 曲线求导(切线向量)
CalculateBezierTangent: 计算贝塞尔曲线上指定t值处的切线向量。
/// <summary>/// 曲线求导(切线向量)/// </summary>/// <param 曲线位置="_CurvePosition"></param>/// <returns></returns>private Vector3 CalculateBezierTangent(float _CurvePosition){//存储计算得到的切线向量Vector3 _Ret = new Vector3(0, 0, 0);//控制点数量int _Number = _CpArr.Count - 1;for (int i = 0; i <= _Number; i++){Vector3 _Pi = _CpArr[i].TransformPoint(new Vector3(0, 0, 0));_Pi = _CpArr[0].InverseTransformPoint(_Pi);//根据贝塞尔曲线的定义,计算贝塞尔基函数的导数项,并与控制点的局部坐标相乘//每次循环迭代,都将计算得到的导数项加到 _Ret 向量上_Ret = _Ret + (-1 * (_Number - i) * Mathf.Pow(1 - _CurvePosition, _Number - i - 1) * Mathf.Pow(_CurvePosition, i) * Cn_m(_Number, i) * _Pi + i * Mathf.Pow(1 - _CurvePosition, _Number - i) * Mathf.Pow(_CurvePosition, i - 1) * Cn_m(_Number, i) * _Pi);}//返回计算得到的切线向量 _Ret,表示贝塞尔曲线上给定参数值 _CurvePosition 对应的切线向量return _Ret;}
BesselCurveDeformation_ZH 完整代码
using System;
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
using UnityEngine.UIElements;/// <summary>
/// 3D贝塞尔曲线变形
/// </summary>
public class BesselCurveDeformation_ZH : MonoBehaviour
{[Header("存储贝塞尔曲线控制点数组")]public List<Transform> _CpArr;[Header("曲线影响力物体")]public Transform _ForceItem;[Range(0, 100f)][Header("控制物体曲线施加力")]public float _Force = 10;[Header("原始顶点位置")]private Vector3[] _OriVertices;[Header("网格数据")]private Mesh _Mesh;[Header("最后一个控制点位置")]//最后一个控制点的位置。用来计算mesh高度来计算tprivate Vector3 _TopPos;void Start(){Initialize();}void Update(){//根据受力,修改控制点UpdateControlPoint();//更新meshUpdateBezierBend();}/// <summary>/// 初始化/// </summary>private void Initialize(){//初始化 控制点数组_CpArr = new List<Transform>();//if (GameObject.Find("Node1").transform != null)//{// //数组清空// _CpArr.Clear();// //获取所有控制端点// _CpArr = GetAllChildren(GameObject.Find("Node").transform);//}//else{GameObject _EmptyObject0 = new GameObject("P0");GameObject _EmptyObject1 = new GameObject("P1");GameObject _EmptyObject2 = new GameObject("P2");GameObject _EmptyObject3 = new GameObject("P3");GameObject _EmptyObject4 = new GameObject("P4");GameObject _EmptyObject5 = new GameObject("P5");_EmptyObject0.transform.SetParent(transform);_EmptyObject0.transform.localPosition=new Vector3(GridCreation_ZH._Instance._MeshHeight/2*-1, 0,0);_EmptyObject1.transform.SetParent(_EmptyObject0.transform);_EmptyObject1.transform.localPosition = new Vector3(0, GridCreation_ZH._Instance._MeshHeight/6, 0);_EmptyObject2.transform.SetParent(_EmptyObject1.transform);_EmptyObject2.transform.localPosition = new Vector3(0, GridCreation_ZH._Instance._MeshHeight / 6, 0);_EmptyObject3.transform.SetParent(_EmptyObject2.transform);_EmptyObject3.transform.localPosition = new Vector3(0, GridCreation_ZH._Instance._MeshHeight / 6, 0);_EmptyObject4.transform.SetParent(_EmptyObject3.transform);_EmptyObject4.transform.localPosition = new Vector3(0, GridCreation_ZH._Instance._MeshHeight / 6, 0);_EmptyObject5.transform.position = new Vector3(0, GridCreation_ZH._Instance._MeshHeight, 0);//_EmptyObject5.transform.eulerAngles=new Vector3(0, 0, 90);_EmptyObject5.transform.SetParent(_EmptyObject4.transform);_CpArr.Add(_EmptyObject0.transform);_CpArr.Add(_EmptyObject1.transform);_CpArr.Add(_EmptyObject2.transform);_CpArr.Add(_EmptyObject3.transform);_CpArr.Add(_EmptyObject4.transform);_CpArr.Add(_EmptyObject5.transform);for (int i = 0; i < _CpArr.Count; i++){if (_CpArr[i].GetComponent<ControlPoint_ZH>() == null){//弯曲端点 受力组件添加_CpArr[i].gameObject.AddComponent<ControlPoint_ZH>();}}}//作用力变量float _CurrentNumber = 90;if (_CpArr.Count > 0){//6个控制点的情况下//其他 自己调节一下for (int i = 0; i < _CpArr.Count; i++){//作用力赋值_CpArr[i].GetComponent<ControlPoint_ZH>()._BendForce = _CurrentNumber; _CurrentNumber /= 2;}}if (_ForceItem==null){_ForceItem = GameObject.Find("ForceCube").transform;}//顶部坐标 获取_TopPos = _CpArr[_CpArr.Count - 1].TransformPoint(new Vector3(0, 0, 0));//相对P0坐标 也就是第一个控制点坐标_TopPos = _CpArr[0].InverseTransformPoint(_TopPos);//网格获取_Mesh = GetComponent<MeshFilter>().mesh;//网格顶点位置获取_OriVertices = (Vector3[])_Mesh.vertices.Clone();//转换成p0的相对坐标for (int i = 0; i < _OriVertices.Length; i++){//世界坐标 局部转世界_OriVertices[i] = transform.TransformPoint(_OriVertices[i]);//相对P0坐标 世界转局部_OriVertices[i] = _CpArr[0].InverseTransformPoint(_OriVertices[i]);}}/// <summary>/// 获取所有子节点/// </summary>/// <param 父节点="_Parent"></param>/// <returns></returns>private List<Transform> GetAllChildren(Transform _Parent){List<Transform> _ListTra = new List<Transform>();foreach (Transform _Child in _Parent){//添加直接子节点_ListTra.Add(_Child);//递归收集后代节点List<Transform> _Descendants = GetAllChildren(_Child);_ListTra.AddRange(_Descendants);}return _ListTra;}/********************************贝塞尔曲线Mesh计算相关*********************************/// 对原来的顶点做贝塞尔曲线变换,得到弯曲变换后对应的点位置/// <summary>/// 控制点更新/// 根据施加在曲线上的力,计算并更新控制点的旋转角度/// </summary>private void UpdateBezierBend(){//曲线弯曲方向Vector3 _BendVector = new Vector3(0, 0, 0);//弯曲布尔 true 无弯曲 false 弯曲bool _IsVertical = true;for (int i = 1; i < _CpArr.Count; i++){//对于每个控制点,将其位置转换为第一个控制点 _CpArr[0] 的局部空间Vector3 _Pos = _CpArr[i].TransformPoint(new Vector3(0, 0, 0));_Pos = _CpArr[0].InverseTransformPoint(_Pos);//判断当前控制点 x z 是否在非零//如果非零 就证明曲线在一个非垂直方向上弯曲if (IsEqualZero(_Pos.x) == false || IsEqualZero(_Pos.z) == false){//临时弯曲变量存储_BendVector.x = _Pos.x;_BendVector.z = _Pos.z;//弯曲布尔_IsVertical = false;break;}}//原始网格顶点数组Vector3[] _Temp = (Vector3[])_Mesh.vertices.Clone();//遍历所有顶点for (int i = 0; i < _OriVertices.Length; i++){//获取顶点坐标,计算t值Vector3 _OriPos = _OriVertices[i];Vector3 _BendPos;//没有弯曲if (_IsVertical == true){//当前顶点位置不变_BendPos = _OriPos;}//发生弯曲else{//将顶点的原始位置 _OriPos 的 y 分量除以顶部控制点 _TopPos 的 y 分量,计算参数 _CurvePositionfloat _T = _OriPos.y / _TopPos.y;//获取顶点在贝塞尔曲线上对应的坐标Vector3 _BezierPos = CalculateBezier(_T);//获取顶点在曲线上应有的法线偏移向量Vector3 _NormalVector = GetBendNormalVector(_T, _OriPos, _BendVector);//获取顶点在曲线上应有的垂直偏移向量Vector3 _VerticalVector = new Vector3(_OriPos.x, 0, _OriPos.z) - Vector3.Project(new Vector3(_OriPos.x, 0, _OriPos.z), _BendVector);//获取顶点最终弯曲位置_BendPos = _BezierPos + _NormalVector + _VerticalVector;}//转换回 mesh 本地坐标系_BendPos = _CpArr[0].TransformPoint(_BendPos);_BendPos = transform.InverseTransformPoint(_BendPos);_Temp[i] = _BendPos;}_Mesh.vertices = _Temp;}/// <summary>/// Bezier 曲线公式/// 计算贝塞尔曲线上给定参数值 _CurvePosition 对应的位置/// </summary>/// <param 曲线位置="_CurvePosition"></param>/// <returns></returns>private Vector3 CalculateBezier(float _CurvePosition){//存储坐标Vector3 _Ret = new Vector3(0, 0, 0);//控制点数量int _Number = _CpArr.Count - 1;for (int i = 0; i <= _Number; i++){//获取第 i 个控制点的世界坐标,通过将其位置从控制点的局部坐标系转换到世界坐标Vector3 _Pi = _CpArr[i].TransformPoint(new Vector3(0, 0, 0));//将转换后的世界坐标再次转换回第一个控制点的局部坐标系,用于与其他控制点进行计算_Pi = _CpArr[0].InverseTransformPoint(_Pi);//根据贝塞尔曲线的定义,计算贝塞尔基函数的乘积项,并与控制点的局部坐标相乘//Cn_m(_Number, i) 是组合数函数 表示从 _Number 个控制点中选择 i 个的组合数_Ret = _Ret + Mathf.Pow(1 - _CurvePosition, _Number - i) * Mathf.Pow(_CurvePosition, i) * Cn_m(_Number, i) * _Pi;}return _Ret;}/// <summary>/// 曲线求导(切线向量)/// </summary>/// <param 曲线位置="_CurvePosition"></param>/// <returns></returns>private Vector3 CalculateBezierTangent(float _CurvePosition){//存储计算得到的切线向量Vector3 _Ret = new Vector3(0, 0, 0);//控制点数量int _Number = _CpArr.Count - 1;for (int i = 0; i <= _Number; i++){Vector3 _Pi = _CpArr[i].TransformPoint(new Vector3(0, 0, 0));_Pi = _CpArr[0].InverseTransformPoint(_Pi);//根据贝塞尔曲线的定义,计算贝塞尔基函数的导数项,并与控制点的局部坐标相乘//每次循环迭代,都将计算得到的导数项加到 _Ret 向量上_Ret = _Ret + (-1 * (_Number - i) * Mathf.Pow(1 - _CurvePosition, _Number - i - 1) * Mathf.Pow(_CurvePosition, i) * Cn_m(_Number, i) * _Pi + i * Mathf.Pow(1 - _CurvePosition, _Number - i) * Mathf.Pow(_CurvePosition, i - 1) * Cn_m(_Number, i) * _Pi);}//返回计算得到的切线向量 _Ret,表示贝塞尔曲线上给定参数值 _CurvePosition 对应的切线向量return _Ret;}/// <summary>/// 获取指定点上的法线向量偏移/// 计算在贝塞尔曲线上给定参数值 _CurvePosition 对应位置的弯曲法向量/// </summary>/// <param 曲线位置="_CurvePosition"></param>/// <param 原始位置="_OriPos"></param>/// <param 弯曲方向="_BendVector"></param>/// <returns></returns>private Vector3 GetBendNormalVector(float _CurvePosition, Vector3 _OriPos, Vector3 _BendVector){//切线斜率Vector3 _TangentVector = CalculateBezierTangent(_CurvePosition);//切线竖直时,顶点在在弯曲向量上的投影向量即为法线向量if (IsEqualZero(_TangentVector.x) == true && IsEqualZero(_TangentVector.z) == true){//直接返回 原始位置 _OriPos 投影到弯曲向量 _BendVector 上的向量,作为法线向量return Vector3.Project(new Vector3(_OriPos.x, 0, _OriPos.z), _BendVector);}//存储计算得到的法线向量Vector3 _NormalVector = new Vector3(0, 0, 0);//计算切线向量与原始位置向量的点乘float _DirectFlag = Vector3.Dot(_BendVector, _OriPos);//判断法线向量朝向(法线向量有两个方向)//大于零 顶点坐标与弯曲方向同向if (_DirectFlag > 0){//切线水平,法线向量竖直向下if (IsEqualZero(_TangentVector.y) == true){_NormalVector.y = -1;}else{//切线朝上,法线向量与切线水平同向if (_TangentVector.y > 0){_NormalVector.x = _TangentVector.x;_NormalVector.z = _TangentVector.z;}//切线朝下,法线向量与切线水平反向else{_NormalVector.x = -_TangentVector.x;_NormalVector.z = -_TangentVector.z;}//使法线向量与切线向量水平且垂直于切线向量_NormalVector.y = -(_TangentVector.x * _NormalVector.x + _TangentVector.z * _NormalVector.z) / _TangentVector.y;}}//小于零 顶点坐标与弯曲方向反向else{//切线水平,法线向量竖直向上if (IsEqualZero(_TangentVector.y) == true){_NormalVector.y = 1;}else{//切线朝上,法线向量与切线水平反向if (_TangentVector.y > 0){_NormalVector.x = -_TangentVector.x;_NormalVector.z = -_TangentVector.z;}//切线朝下,法线向量与切线水平同向else{_NormalVector.x = _TangentVector.x;_NormalVector.z = _TangentVector.z;}//使得法线向量与切线向量水平且垂直于切线向量_NormalVector.y = -(_TangentVector.x * _NormalVector.x + _TangentVector.z * _NormalVector.z) / _TangentVector.y;}}//计算法线向量的模//法线向量的模应为到投影到弯曲面后,到中心点的距离float _Magnitude = Vector3.Project(new Vector3(_OriPos.x, 0, _OriPos.z), _BendVector).magnitude;//将法线向量按照该模进行缩放,使其长度与距离一致_NormalVector = _NormalVector.normalized * _Magnitude;//返回法线向量return _NormalVector;}/// <summary>/// 浮点判断是否为零/// </summary>/// <param 值="_Value"></param>/// <returns></returns>private bool IsEqualZero(float _Value){return Mathf.Abs(_Value) < 1e-5;}/// <summary>/// 组合数函数/// 表示从 _Number 个控制点中选择 i 个的组合数/// </summary>/// <param 控制点="_Number"></param>/// <param 组合数="m"></param>/// <returns></returns>private int Cn_m(int n, int m){int _Ret = 1;for (int i = 0; i < m; i++){_Ret = _Ret * (n - i) / (i + 1);}return _Ret;}/************************************根据受力情况计算控制点坐标(旋转)*****************************//// <summary>/// 更新控制点的旋转角度/// 根据受力计算各个控制点的旋转角度/// </summary>private void UpdateControlPoint(){//受力强度float _HandleForce = _Force;//根据受力计算各个控制点旋转角度for (int i = 1; i <= _CpArr.Count - 2; i++){//计算最大弯曲方向Vector3 _ForcePos = _ForceItem.transform.TransformPoint(new Vector3(0, 0, 0));_ForcePos = _CpArr[i - 1].InverseTransformPoint(_ForcePos);//计算从控制点到受力位置的向量Vector3 _ToVector = _ForcePos - _CpArr[i].localPosition;//得到该控制点的旋转角度Quaternion _MaxRotation = Quaternion.FromToRotation(Vector3.up, _ToVector);//获取控制点组件ControlPoint_ZH _Cp = _CpArr[i].gameObject.GetComponent<ControlPoint_ZH>();//计算弯曲比例 float _RotateRate = Mathf.Clamp(_HandleForce / _Cp._BendForce, 0f, 1.0f);//设置旋转角度_CpArr[i].localRotation = Quaternion.Lerp(Quaternion.Euler(0, 0, 0), _MaxRotation, _RotateRate);}}
}自定义网格创建
在Unity中,网格是由一系列顶点、三角形面和纹理坐标组成的。
通过创建网格,我们可以实现各种形状和模型的生成。
在示例代码中,我们可以看到通过使用Unity的Mesh和MeshFilter组件。
以及C#脚本中的数据结构和方法,实现了一个具有多个相位的简单网格的动态生成。
该网格可以用于游戏场景、建筑模型等各种应用。
使用Unity的 Mesh 和 MeshFilter 组件:这些组件允许我们创建和管理网格。
Mesh 用于存储网格的几何数据,而 MeshFilter 用于将Mesh附加到游戏对象上。
GridCreation_ZH 完整代码
using System.Collections;
using System.Collections.Generic;
using UnityEngine;/// <summary>
/// 网格创建
/// 动态生成一个具有多个相位的简单网格,可以根据需求调整网格的宽度、高度、相位数量和末端宽度
/// 以获得不同形状和细分程度的网格
/// </summary>
public class GridCreation_ZH : MonoBehaviour
{//单例public static GridCreation_ZH _Instance;[Header("网格宽度")]public float _MeshWidth = 1f;[Header("网格高度")]public float _MeshHeight = 10f;[Header("网格分段数")]public int _PhaseCount = 20;[Header("网格末端宽度")]public float _EndWidth = 0.1f;void Awake(){_Instance = this;//计算每个相位的高度float _PhaseHeight = _MeshHeight / (_PhaseCount - 1);//计算每个相位的宽度float _DecreaseWidth = (_MeshWidth - _EndWidth) / (_PhaseCount - 1);//顶点数组//长度为 _PhaseCount * 6,每个相位有 6 个顶点Vector3[] _Vertices = new Vector3[_PhaseCount * 6];float _BottomY = -_MeshHeight * 0.5f;for (int i = 0; i < _PhaseCount; i++){//根据当前相位的索引计算每个顶点的位置//并将其存储在 _Vertices 数组中float _CurWidth = _MeshWidth - _DecreaseWidth * i;_Vertices[i * 6 + 0] = new Vector3(_BottomY + i * _PhaseHeight, (_CurWidth / 2), 0);_Vertices[i * 6 + 1] = new Vector3(_BottomY + i * _PhaseHeight, (_CurWidth / 4), -Mathf.Sqrt(3) * _CurWidth / 4);_Vertices[i * 6 + 2] = new Vector3(_BottomY + i * _PhaseHeight, -(_CurWidth / 4), -Mathf.Sqrt(3) * _CurWidth / 4);_Vertices[i * 6 + 3] = new Vector3(_BottomY + i * _PhaseHeight, -(_CurWidth / 2), 0);_Vertices[i * 6 + 4] = new Vector3(_BottomY + i * _PhaseHeight, -(_CurWidth / 4), Mathf.Sqrt(3) * _CurWidth / 4);_Vertices[i * 6 + 5] = new Vector3(_BottomY + i * _PhaseHeight, (_CurWidth / 4), Mathf.Sqrt(3) * _CurWidth / 4);}//法线数组//长度也为 _PhaseCount * 6,与顶点数组相对应Vector3[] _Normals = new Vector3[_PhaseCount * 6];for (int i = 0; i < _PhaseCount; i++){//根据当前相位的索引计算每个顶点的法线方向,并将其存储在 _Normals 数组中float _CurWidth = _MeshWidth - _DecreaseWidth * i;_Normals[i * 6 + 0] = new Vector3(0, (_CurWidth / 2), 0).normalized;_Normals[i * 6 + 1] = new Vector3(0, (_CurWidth / 4), -Mathf.Sqrt(3) * _CurWidth / 4).normalized;_Normals[i * 6 + 2] = new Vector3(0, -(_CurWidth / 4), -Mathf.Sqrt(3) * _CurWidth / 4).normalized;_Normals[i * 6 + 3] = new Vector3(0, -(_CurWidth / 2), 0).normalized;_Normals[i * 6 + 4] = new Vector3(0, -(_CurWidth / 4), Mathf.Sqrt(3) * _CurWidth / 4).normalized;_Normals[i * 6 + 5] = new Vector3(0, (_CurWidth / 4), Mathf.Sqrt(3) * _CurWidth / 4).normalized;}//三角形索引数组//长度为 (_PhaseCount - 1) * 6 * 6,每个相位之间的相邻顶点构成一个三角形int[] _Indices = new int[(_PhaseCount - 1) * 6 * 6];for (int i = 1; i < _PhaseCount; i++){for (int j = 0; j < 6; j++){//嵌套循环遍历,根据相邻顶点的索引,构建三角形的索引,并将其存储在 _Indices 数组中int nextIndex = (j + 1) % 6;_Indices[(i - 1) * 6 * 6 + j * 6 + 0] = (i - 1) * 6 + j;_Indices[(i - 1) * 6 * 6 + j * 6 + 1] = i * 6 + nextIndex;_Indices[(i - 1) * 6 * 6 + j * 6 + 2] = (i - 1) * 6 + nextIndex;_Indices[(i - 1) * 6 * 6 + j * 6 + 3] = (i - 1) * 6 + j;_Indices[(i - 1) * 6 * 6 + j * 6 + 4] = i * 6 + j;_Indices[(i - 1) * 6 * 6 + j * 6 + 5] = i * 6 + nextIndex;}}//将之前计算得到的顶点、法线和三角形索引分别赋值给网格的对应属性,创建了一个简单的网格Mesh _Mesh = GetComponent<MeshFilter>().mesh;_Mesh.vertices = _Vertices;_Mesh.normals = _Normals;_Mesh.triangles = _Indices;transform.position = Vector3.up * 5;transform.eulerAngles = new Vector3(0, 0, 90);}
}GridCreation_ZH 搭载
记得在空物体上添加:Mesh Renderer、Mesh Filter 组件。

Hierarchy 窗口:

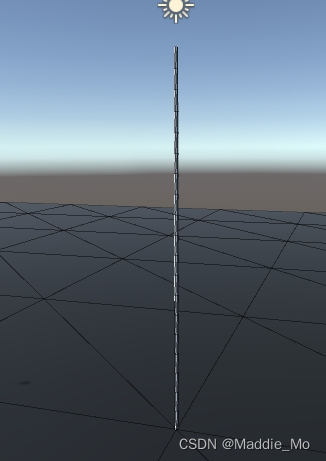
自定义网格创建 运行效果

网格创建和曲线变形 运行情况
Hierarchy 窗口:
运行效果:
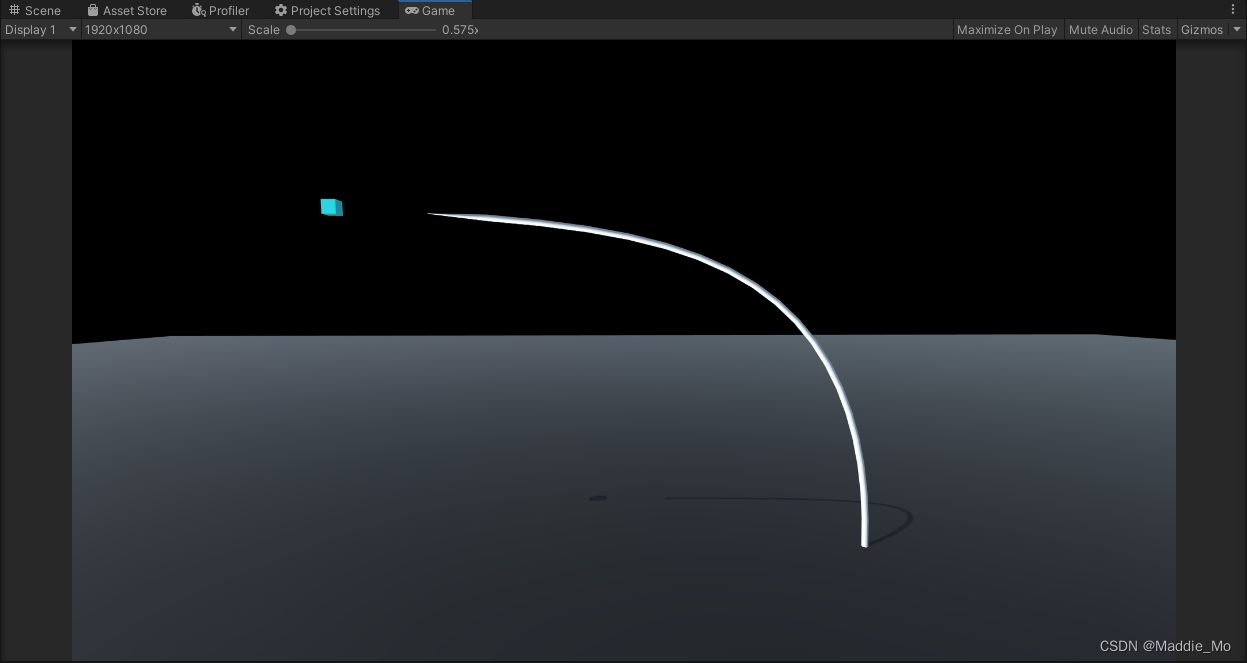
除了以上示例代码,还有其他相关的技术和工具可以扩展和优化网格创建和曲线变形效果。
例如,使用Shader进行高级的顶点变形和着色效果、使用插件或库来简化曲线绘制和变形操作等。通过深入学习和实践这些技术,您可以在Unity中创建出更加生动和富有创意的场景和模型。
掌握网格创建和曲线变形的原理和方法,将为您的游戏开发和视觉效果设计带来更多的可能性和灵活性。
希望这些信息能够进一步满足您对Unity中 网格创建和曲线变形的需求。
如果您有任何特定的问题或需要更深入的讨论,请随时提出。
路漫漫其修远兮,与君共勉。
相关文章:

Unity中的网格创建和曲线变形
Unity中的网格创建和曲线变形 3D贝塞尔曲线变形贝塞尔曲线基础线性公式二次方公式三次方公式 Unity 实现3D贝塞尔曲线变形准备工作脚本概述变量定义 变量解析函数解析 获取所有子节点GetAllChildren 获取所有子节点UpdateBezierBend 控制点更新CalculateBezier Bezier 曲线公式…...

day0 3r文档docker部署
3R编码 | 3R教室 - 最好的数字游民学习与交流俱乐部! (3rcd.com) window安装wsl下载不下来,正好有个服务器,就用linux吧密钥长度不匹配,设置一下长度即可 文档启动不成功,单独下载了下nginx,docker pull nginx:latest …...
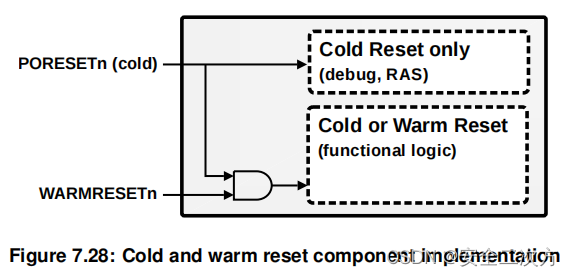
PSCA复位控制集成之复位信号
组件可能支持两种基本的复位类型。 • 冷复位:重置组件中的所有逻辑。用作上电复位。 • 热复位:重置组件中的大部分逻辑。通常,复位的范围是所有功能逻辑。不包括在热复位中的逻辑会随组件类型而变化,但通常会排除诸如调试和 R…...

C#,数值计算,数据测试用的对称正定矩阵(Symmetric Positive Definite Matrix)的随机生成算法与源代码
C.Hermite 1、对称矩阵 对称矩阵(Symmetric Matrices)是指以主对角线为对称轴,各元素对应相等的矩阵。在线性代数中,对称矩阵是一个方形矩阵,其转置矩阵和自身相等。1855年,埃米特(C.Hermite,1822-1901年)证明了别的数学家发现的一些矩阵类的特征根的特殊性质,如称为埃…...

EventWaitHandle 和 lock使用区别
EventWaitHandle 和 lock 语句在 C# 中都是用于线程同步的机制,但它们之间有着显著的区别和不同的使用场景。下面是它们之间的主要对比和区别: EventWaitHandle 定义:EventWaitHandle 是用于跨进程或跨线程同步的低级别同步原语。它允许一个…...
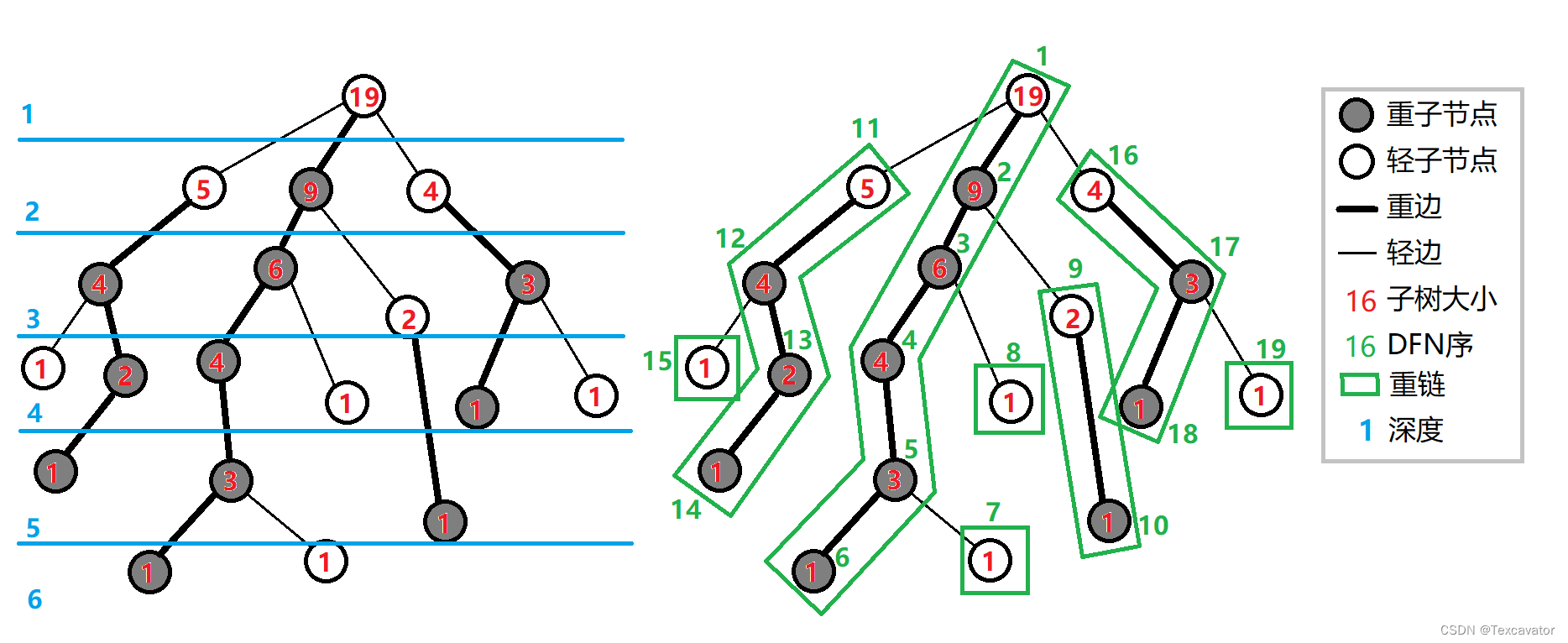
【图论】树链剖分
本篇博客参考: 【洛谷日报#17】树链剖分详解Oi Wiki 树链剖分 文章目录 基本概念代码实现常见应用路径维护:求树上两点路径权值和路径维护:改变两点最短路径上的所有点的权值求最近公共祖先 基本概念 首先,树链剖分是什么呢&…...

Requests教程-17-请求代理设置
上一小节我们学习了requests解决乱码的方法,本小节我们讲解一下requests设置代理的方法。 代理基本原理 代理实际上指的就是代理服务器, 英文叫作proxy server ,它的功能是代理网络用户去取得网络信息。形象地说,它是网络信息的中…...

python内置函数 G
python内置函数 G Python 解释器内置了很多函数和类型,任何时候都能使用。 G 名称描述getattr从对象中获取属性值。globals返回当前全局符号表的字典。 getattr(object, name) getattr(object, name) getattr(object, name, default) getattr() 是 Python 中…...
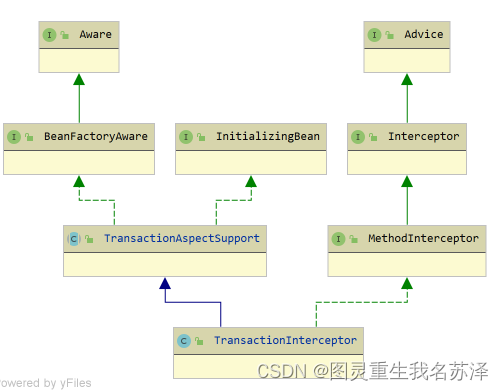
深入了解 Spring boot的事务管理机制:掌握 Spring 事务的几种传播行为、隔离级别和回滚机制,理解 AOP 在事务管理中的应用
🎉🎉欢迎光临,终于等到你啦🎉🎉 🏅我是苏泽,一位对技术充满热情的探索者和分享者。🚀🚀 🌟持续更新的专栏《Spring 狂野之旅:从入门到入魔》 &a…...

机械产品CE-MD认证测试项目介绍
机械产品CE-MD认证测试项目介绍 一、引言 随着欧洲市场的日益开放和全球化进程的加速,越来越多的机械产品进入欧洲市场。为确保这些产品的安全性和符合性,欧洲联盟(EU)引入了CE认证制度。同时,对于医疗器械类产品&…...
金融知识分享系列之:MACD指标精讲
金融知识分享系列之:MACD指标精讲 一、MACD指标二、指标原理三、MACD指标参考用法四、MACD计算步骤五、MACD分析要素六、根据快线DIF位置判断趋势七、金叉死叉作为多空信号八、快线位置交叉信号九、指标背离判断行情反转十、差离值的正负十一、差离值的变化十二、指…...

王道c语言-100元有几种换法
Description 一张面值100元的人民币换成10元、5元、2元和1元面值的票子。要求换正好40张,且每种票子至少一张。问:有几种换法? #include <stdio.h> int main() {int count 0;int i, j, t, k, ret 0;for (i 1; i < 37; i) {for …...

c++野指针如何处理?
什么是野指针? 野指针指向一个已删除的对象或未申请访问受限内存区域的指针。与空指针不同,野指针无法通过简单地判断是否为NULL避免,而只能通过养成良好的编程习惯来尽力减少,对野指针进行操作很容易造成程序错误。 野指针产生…...
关于大根堆,set重载运算符
题目描述 \,\,\,\,\,\,\,\,\,\,制定合理的日程能够帮助利用好时间进行加训,加训和加训。 \,\,\,\,\,\,\,\,\,\,新学期开始了,应该好好学习了!凌晨两点整,加睡失败的你在为新一天的各项重要事件制定闹钟。 \,\,\,\,\,\,\,\,\,\, \,…...

Algae c++
描述 问题陈述 池塘中藻类的发展情况如下。 假设年初i水藻的总重量为xi克。对于 i≥2000,下列公式成立: xi1rxi−D 给你r、D和x2000。请依次计算 x2001、...、x2010 并打印出来。 输入描述 输入内容由标准输入法提供,格式…...

开发常用的一些工具总结
开发常用的一些工具总结 记录一些常用的开发软件. Android 开发相关 : Android studio 安卓开发者必备的编辑器,也是我用过最好用的编辑器.还可以用来写JNI 和C.Android studio 插件 : GsonFormatLeakCanary 其他 VS Code :轻量级的开发工具,插件非常多,很好用,但是上手难度…...

k8s Yaml语法解析
YAML是一个类似 XML、JSON 的标记性语言。它强调以数据为中心,并不是以标识语言为重点。因而YAML本身的定义比较简单,号称"一种人性化的数据格式语言"。 YAML的语法比较简单,主要有下面几个: 1、大小写敏感 2、使用缩进…...

【晴问算法】提高篇—动态规划专题—最长公共子序列
题目描述 现有两个字符串s1与s2,求s1与s2的最长公共子序列的长度(子序列可以不连续)。 输入描述 第一行为字符串s1,仅由小写字母组成,长度不超过100; 第一行为字符串s2…...

Greetings
Problem - 1915F - Codeforces 题意 给一些(l,r)找到所有能够包含(l,r)的数目 引入 也就是找逆序对个数 要用到归并排序中的思想: //https://www.luogu.com.cn/problem/P1216 #include<iostream> #include<cstdio> #include<stack> #include…...

JS03-函数
函数 使用函数 // 函数声明function sayHi(){document.write(Hello!<br>)}for(let i 1; i < 6; i){// 函数调用sayHi()}函数封装 function getScore(arr){sum 0for( let i 0; i < arr.length; i){sum arr[i]}document.write(sum)}getScore([99, 66, 100])函数…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...
