【概率论中的两种重要公式:全概率和贝叶斯】
贝叶斯公式(Bayes’ Theorem)是概率论中的一条重要定理,用于计算条件概率。它描述了在已知某一事件发生的条件下,另一事件发生的概率。贝叶斯公式如下所示:
P ( A ∣ B ) = P ( B ∣ A ) ⋅ P ( A ) P ( B ) P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)⋅P(A)
其中:
- P ( A ∣ B ) P(A|B) P(A∣B):表示在事件B发生的条件下事件A发生的概率,即A的后验概率。
- P ( B ∣ A ) P(B|A) P(B∣A):表示在事件A发生的条件下事件B发生的概率,即B的条件概率。
- P ( A ) P(A) P(A)和 P ( B ) P(B) P(B):分别表示事件A和事件B的先验概率。
全概率公式(Law of Total Probability)用于计算一个事件的概率,通过将该事件分解成多个互斥事件的并集,并利用这些互斥事件的概率求和来计算目标事件的概率。全概率公式如下所示:
P ( B ) = ∑ i P ( B ∣ A i ) ⋅ P ( A i ) P(B) = \sum_{i} P(B|A_i) \cdot P(A_i) P(B)=i∑P(B∣Ai)⋅P(Ai)
其中: - A i A_i Ai是样本空间的一个划分,表示一系列互斥事件。
- P ( B ∣ A i ) P(B|A_i) P(B∣Ai)是在给定事件 A i A_i Ai下事件B的条件概率。
- P ( A i ) P(A_i) P(Ai)是事件 A i A_i Ai的概率。
主要用法区别: - 贝叶斯公式主要用于计算已知某一事件发生的条件下另一事件发生的概率,常用于推断问题,如医学诊断、垃圾邮件过滤等。
- 全概率公式主要用于计算目标事件的概率,通过将目标事件分解成多个互斥事件的并集,并利用这些事件的概率求和来计算目标事件的概率。
具体例子:
- 贝叶斯公式示例:
- 问题:假设有一种罕见的疾病,已知该疾病发生率为0.1%。医生发现一名患者呈阳性反应,测试的准确率为99%。求该患者确实患有该疾病的概率。
- 解答:设事件 A A A表示患者确实患有疾病,事件 B B B表示测试呈阳性。已知 P ( A ) = 0.001 P(A)=0.001 P(A)=0.001, P ( B ∣ A ) = 0.99 P(B|A)=0.99 P(B∣A)=0.99,需要求 P ( A ∣ B ) P(A|B) P(A∣B)。
根据贝叶斯公式:
P ( A ∣ B ) = P ( B ∣ A ) ⋅ P ( A ) P ( B ) = 0.99 ⋅ 0.001 P ( B ) P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)} = \frac{0.99 \cdot 0.001}{P(B)} P(A∣B)=P(B)P(B∣A)⋅P(A)=P(B)0.99⋅0.001
根据全概率公式:
P ( B ) = P ( B ∣ A ) ⋅ P ( A ) + P ( B ∣ ¬ A ) ⋅ P ( ¬ A ) = 0.99 ⋅ 0.001 + P ( B ∣ ¬ A ) ⋅ ( 1 − 0.001 ) P(B) = P(B|A) \cdot P(A) + P(B|\neg A) \cdot P(\neg A) = 0.99 \cdot 0.001 + P(B|\neg A) \cdot (1-0.001) P(B)=P(B∣A)⋅P(A)+P(B∣¬A)⋅P(¬A)=0.99⋅0.001+P(B∣¬A)⋅(1−0.001)
其中, P ( B ∣ ¬ A ) P(B|\neg A) P(B∣¬A)表示患者没有疾病但测试呈阳性的概率,通常称为误报率,这里假设为0.01。
P ( B ) = 0.99 ⋅ 0.001 + 0.01 ⋅ ( 1 − 0.001 ) P(B) = 0.99 \cdot 0.001 + 0.01 \cdot (1-0.001) P(B)=0.99⋅0.001+0.01⋅(1−0.001)
最终求得 P ( A ∣ B ) P(A|B) P(A∣B)。
- 全概率公式示例:
- 问题:假设有两个工厂生产某种产品,工厂A的产品有20%的缺陷率,工厂B的产品有10%的缺陷率。已知购买该产品的人中,80%来自工厂A,20%来自工厂B。求购买的产品中有缺陷的概率。
- 解答:设事件 D D D表示产品有缺陷,事件 F A F_A FA表示产品来自工厂A,事件 F B F_B FB表示产品来自工厂B。需要求 P ( D ) P(D) P(D)。
根据全概率公式:
P ( D ) = P ( D ∣ F A ) ⋅ P ( F A ) + P ( D ∣ F B ) ⋅ P ( F B ) P(D) = P(D|F_A) \cdot P(F_A) + P(D|F_B) \cdot P(F_B) P(D)=P(D∣FA)⋅P(FA)+P(D∣FB)⋅P(FB)
P ( D ) = 0.2 ⋅ 0.8 + 0.1 ⋅ 0.2 P(D) = 0.2 \cdot 0.8 + 0.1 \cdot 0.2 P(D)=0.2⋅0.8+0.1⋅0.2
最终求得购买的产品中有缺陷的概率。
相关文章:

【概率论中的两种重要公式:全概率和贝叶斯】
贝叶斯公式(Bayes’ Theorem)是概率论中的一条重要定理,用于计算条件概率。它描述了在已知某一事件发生的条件下,另一事件发生的概率。贝叶斯公式如下所示: P ( A ∣ B ) P ( B ∣ A ) ⋅ P ( A ) P ( B ) P(A|B) \…...

python中的闭包
一、闭包 1、作用域 在Python代码中,作用域分为两种情况:全局作用域 与 局部作用域 2、变量的作用域 在全局定义的变量 > 全局变量 在局部定义的变量 > 局部变量 3、全局变量与局部变量的访问范围 ① 在全局作用域中可以访问全局变量&#…...

成功解决RuntimeError: OpenSSL 3.0‘s legacy provider failed to load
报错 RuntimeError: OpenSSL 3.0s legacy provider failed to load. This is a fatal error by default, but cryptography supports running without legacy algorithms by setting the environment variable CRYPTOGRAPHY_OPENSSL_NO_LEGACY. If you did not expect this er…...

【 React 】React 组件之间如何通信?
相关文章: React Context的使用方法 react Provider Consumer 使用方法 1. 是什么 我们将组件间通信可以拆分为两个词: 组件通信 组件是vue中最强大的功能之一,同样组件化是React的核心思想 相比vue,React的组件更加灵活和多样…...
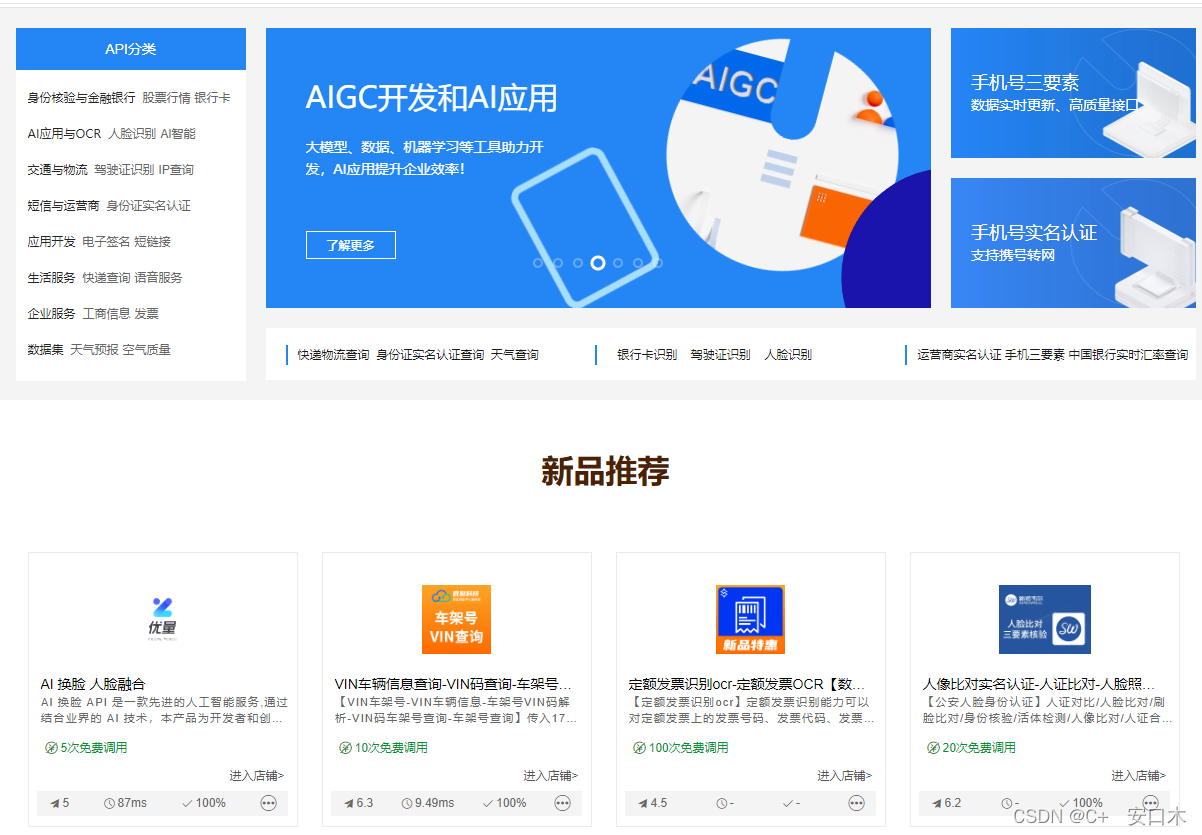
汇总全网免费API,持续更新(新闻api、每日一言api、音乐。。。)
Public&FreeAPI 网址:apis.whyta.cn (推荐) UomgAPI 网址:https://api.uomg.com 教书先生 网址:https://api.oioweb.cn/ 山海API https://api.shserve.cn/ 云析API铺 https://api.a20safe.com/ 韩小韩…...

Android SystemServer进程解析
SystemServer进程在android系统中占了举足轻重的地位,系统的所有服务和SystemUI都是由它启动。 一、SystemServer进程主函数流程 1、主函数三部曲 //frameworks/base/services/java/com/android/server/SystemServer.java /** * The main entry point from zy…...

Github主页设置贪吃蛇详细教程
先看最终实现结果: 有条贪吃蛇放在主页还是蛮酷的哈哈哈。接下来我来讲一讲怎么在Github主页添加一条贪吃蛇。 首先要修改自己的Github的主页,我们得有一个特殊的仓库——这个仓库必须与你的Github用户名保持一致,并且需要公开,…...

二、实现fastdfs文件上传与延迟删除功能的Spring Boot项目
如何在Spring Boot项目中集成FastDFS实现文件上传功能,并添加支持延迟删除功能的实现。 一、Spring Boot 中集成 fastdfs 使用 1、文件上传功能实现 首先,让我们看一下如何实现文件上传功能的接口方法: RestController public class File…...
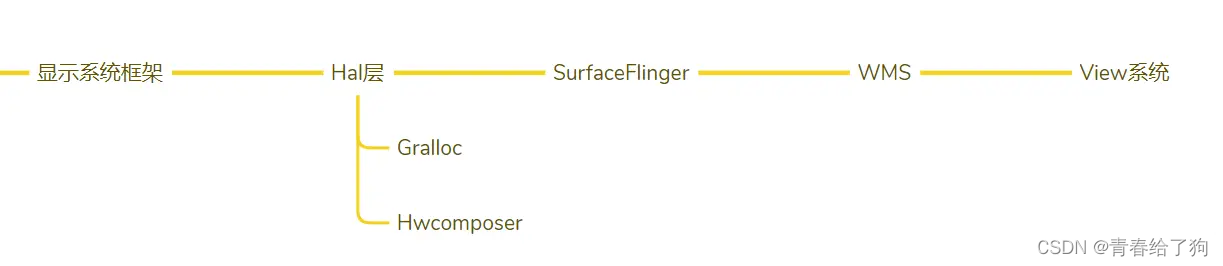
Android FrameWork 学习路线
目录 前言 学习路线: 1.基础知识 2、AOSP 源码学习 3. AOSP 源码编译系统 4. Hal与硬件服务 5.基础组件 6. Binder 7. 系统启动过程分析 8. 应用层框架编辑 9. 显示系统 10. Android 输入系统 11. 系统应用 前言 Android Framework 涉及的行业相当广…...

前端开发者如何打造自己的生态以及ip
作为独立开发者,在公司的岗位上面,经常面对的是页面,但我们不能局限页面,页面是切入点。 1在需求页面的过程中,我们会接触ui,原型,软件,需求, 2在接口对接的过程中&#…...
C语言实现一个两个数加减乘除的答题代码(含文件保存),用户增加,题目增加,题目测试,题目答题等等
目录 1、这是我大一自己写的小代码,现在翻到了就分享出来,高手勿喷。 2、项目运行 3、获取完整源码网址 1、这是我大一自己写的小代码,现在翻到了就分享出来,高手勿喷。 2、项目运行 (1)测试模块 每次…...
YOLOv9改进策略:注意力机制 | 用于微小目标检测的上下文增强和特征细化网络ContextAggregation,助力小目标检测,暴力涨点
💡💡💡本文改进内容:用于微小目标检测的上下文增强和特征细化网络ContextAggregation,助力小目标检测 yolov9-c-ContextAggregation summary: 971 layers, 51002153 parameters, 51002121 gradients, 238.9 GFLOPs 改…...

基于单片机的老人防丢系统设计
目 录 摘 要 I Abstract II 引 言 3 1 系统总体架构 6 1.1方案设计与选择 6 1.2 系统架构设计 6 1.3 系统器件选择 7 2 系统硬件设计 9 2.1 单片机外围电路设计 9 2.2 LCD1602液晶显示电路设计 12 2.3 短信模块电路设计 14 2.4 GPS模块电路设计 14 2.5 电源与按键控制电路设计…...

从海外开发者大会的亲身体悟聊起,谈谈 AI 与开发者关系的重构 | 编码人声
本期「编码人声」节目中,我们聚焦于「AI 与开发者关系的重构」这一主题,从嘉宾参加海外开发者大会的亲身体验开始分享,聊一聊 AI 技术如何影响开发者社区和生态,以及开发者如何在这一变革中找到新的位置。 我们邀请了开发者社区与…...
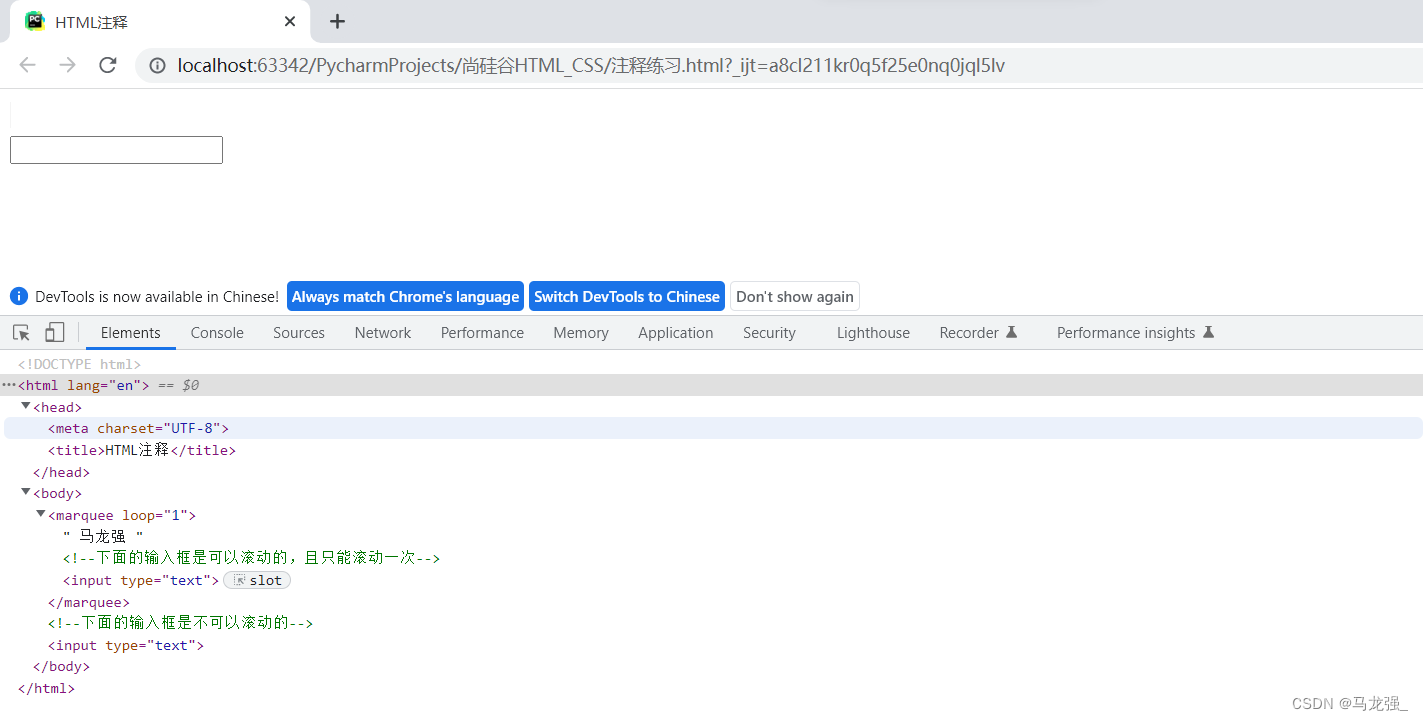
HTML_CSS练习:HTML注释
一、代码示例 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>HTML注释</title> </head> <body><marquee loop"1">马龙强<!--下面的输入框是可以滚动的&#x…...

面试官问我Java异步编程用过吗?我直接说了6种方式!
文章目录 线程池 Runnable/Callable线程池 FutureCompletableFuture线程池 Async注解Spring 事件创建事件事件发布者事件监听器调用事件 消息队列生产者消费者 在实际开发中有些耗时操作,或者对主流程不是那么重要的逻辑,可以通过异步的方式去执行&am…...
一维坐标的移动(bfs)
在一个长度为n的坐标轴上,小S想从A点移动B点。 他的移动规则如下: 向前一步,坐标增加1。 向后一步,坐标减少1。 跳跃一步,使得坐标乘2。 小S不能移动到坐标小于0或大于n的位置。 小S想知道从A点移动到B点的最少步数是多…...

面试题 整理
第1题:常见数据类型大小 这边以64位计算机系统,环境而言。 类型 存储大小 值范围 char 1 字节 -128 到 127 或 0 到 255 unsigned char 1 字节 0 到 255 signed char 1 字节 -128 到 127 int 4 字节 -32,768 到 32,767 或 -2,147,483,648…...
苍穹外卖-day08:导入地址簿功能代码(单表crud)、用户下单(业务逻辑)、订单支付(业务逻辑,cpolar软件)
苍穹外卖-day08 课程内容 导入地址簿功能代码用户下单订单支付 功能实现:用户下单、订单支付 用户下单效果图: 订单支付效果图: 1. 导入地址簿功能代码(单表crud) 1.1 需求分析和设计 1.1.1 产品原型(…...

Java面试相关问题
一.MySql篇 1优化相关问题 1.1.MySql中如何定位慢查询? 慢查询的概念:在MySQL中,慢查询是指执行时间超过一定阈值的SQL语句。这个阈值是由long_query_time参数设定的,它的默认值是10秒1。也就是说,如果一条SQL语句的执…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...
