C语言学习--八种排序算法
目录
排序的概念
1.直接插入排序
基本思想
代码实现
算法分析
2.希尔排序
基本思想
代码实现
算法分析
3.冒泡排序
基本思想
代码实现
算法分析
4.快速排序
基本思想
代码实现
算法分析
5.简单选择排序
基本思想
代码实现
算法分析
6.堆排序
基本思想
代码实现
算法分析
7.归并排序
基本思想
代码实现
算法分析
8.基数排序
基本思想
代码实现
算法分析
总结
排序的概念
排序:所谓排序,就是一串记录,按照某个关键字的大小,按照递增或者递减的顺序进行排列的操作。
稳定性:排序的稳定性,在排序前,有许多相同关键字的记录,他们是按照一定的次序排列的。在排序后,还能按照原先的次序进行排序,那么我们称这种排序算法是稳定的,否则是不稳定的。
内部排序:数据全部在内存中排序。
外部排序:数据元素过多,无法在内存中排序,需要通过内外存之间移动数据来进行排序。
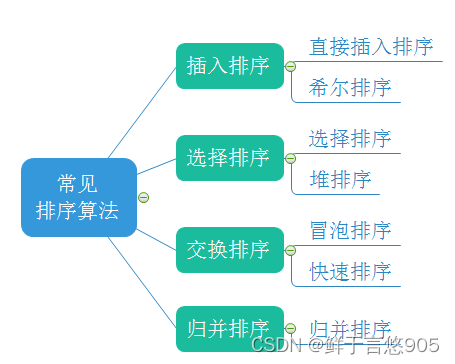
相关算法:
1.直接插入排序
基本思想
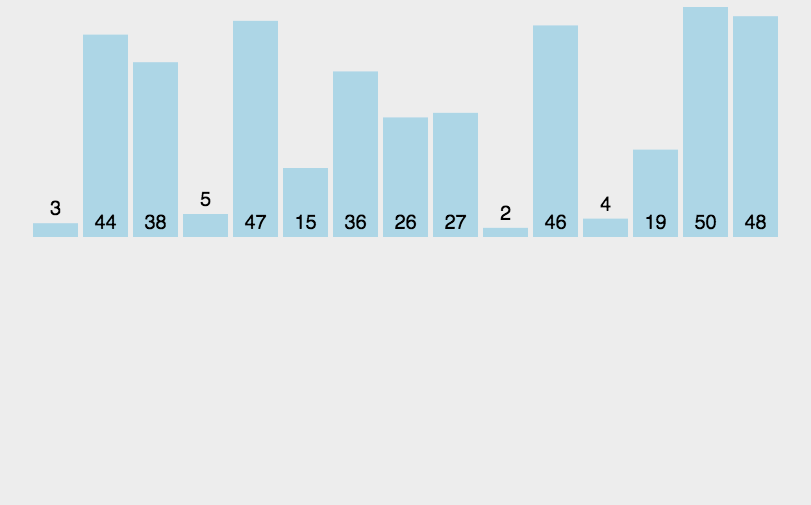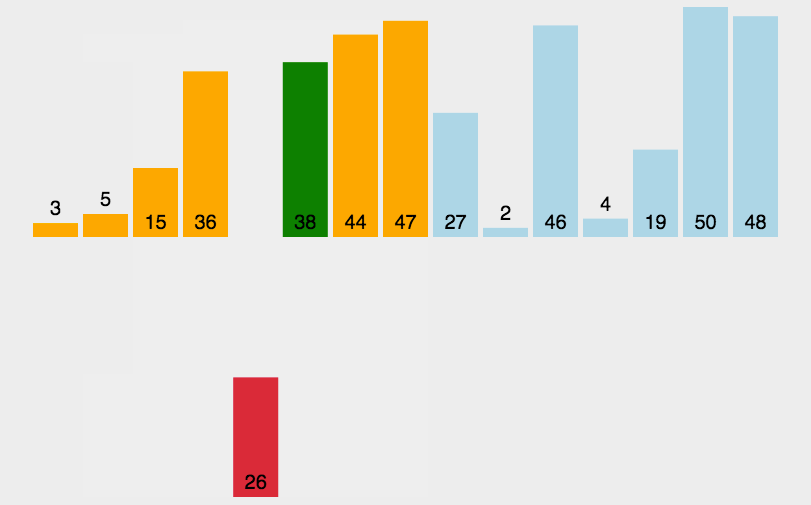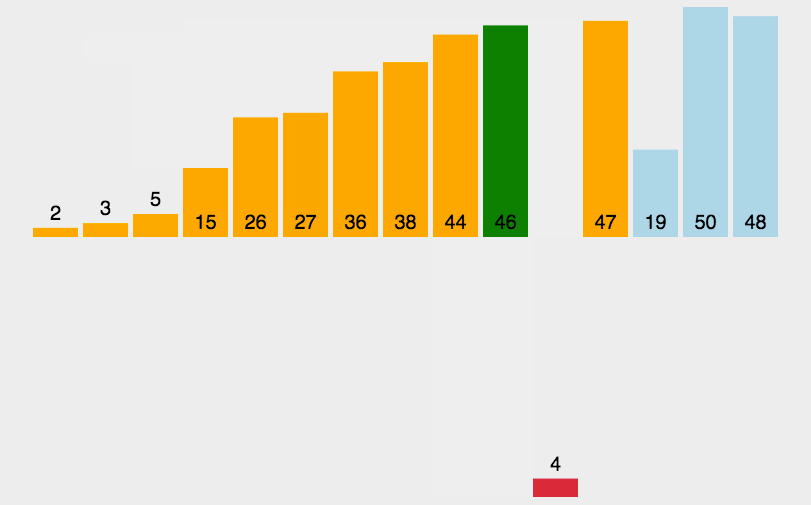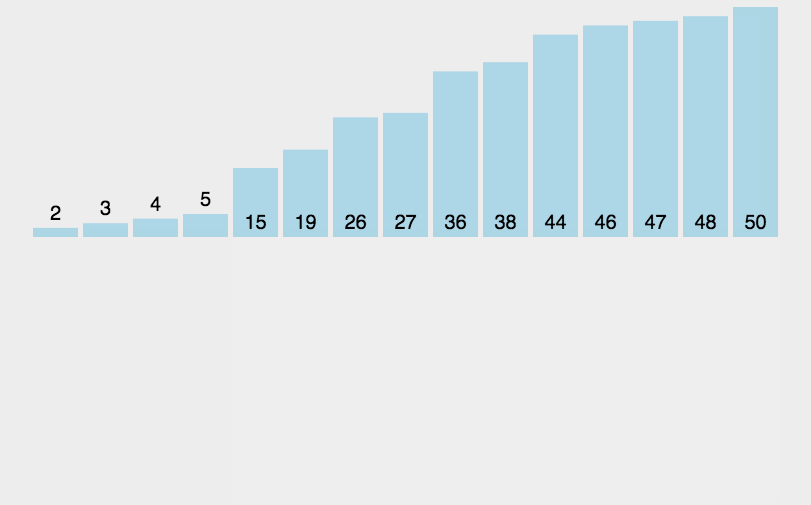
直接插入排序是一种简单的插入排序,思想是把待排序的记录按照其关键值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完成,得到一个新的有序序列。

就比如说,我们现实生活中的玩扑克牌的方式就用了这种思想,我们每摸到一张牌的时候,原先手上的牌是排好序的,我们拿到这张新的牌,会插入到原先的有序序列,然后插入之后,我们新的序列又是有序的。之后,每次摸牌都按照这种方式,最终会得到一个完全有序的序列。
代码实现
有两种一种是直接插入,另一种是折半插入,区别在于查找插入位置的方法不同而已。
//1.直接插入排序void InsertSort(int *a,int n){int j;for(int i=1;i<n;i++){if(a[i]<a[i-1]){int temp=a[i];for( j=i-1;j>=0&&a[j]>temp;j--){a[j+1]=a[j];}//找到temp需要插入的位置,并将元素后以一个//j等于a[j+1]=temp;}}
}1.2.折半插入排序void InsertSort2(int *a,int n){int i,j,low,high,mid;for(i=1;i<n;i++){int temp=a[i];low=0;high=i-1;while(low<=high){mid=(low+high)/2;if(a[mid]>temp){high=mid-1;}else{low=mid+1;}}//of while找到插入的位置for(j=i-1;j>=high+1;j--){a[j+1]=a[j];}a[high+1]=temp;}
} 算法分析
首先,我们先分析算法的时间复杂度,要考虑算法的最好、最坏以及平均复杂度。最好的情况是当这个数组已经有序或者接近有序的情况下,我们只需要进行比较,不需要移动元素,最好时间复杂度为O(N)。而最坏的情况是,这个数组是完全逆序的时候,我们每次比较后,都要移动大量的元素,最坏时间复杂度为O(N2)**,平均复杂度为**O(N^2)。
那么,这个算法的空间复杂度为O(1),因为只需要使用常量级别的空间。
最后,这个算法是否稳定,答案是稳定的。因为每次是从后往前依次比较,不会改变原先的次序,移动的过程中也是一个一个进行移动的。
2.希尔排序
基本思想
希尔排序也是插入排序中的一种,因为其本质就是使用了插入排序,我们从插入排序的结论中可以得出,越接近有序的数组使用插入排序的效率越高。
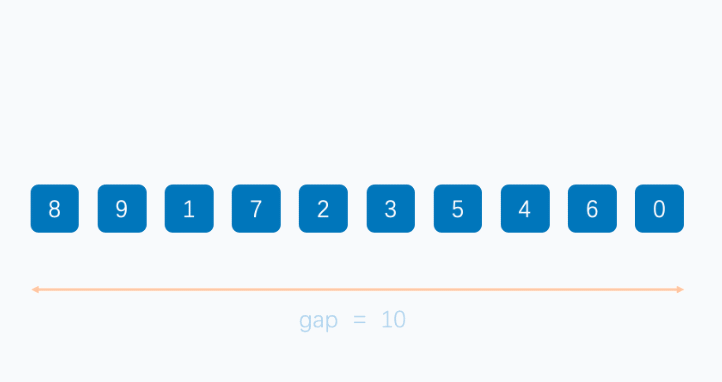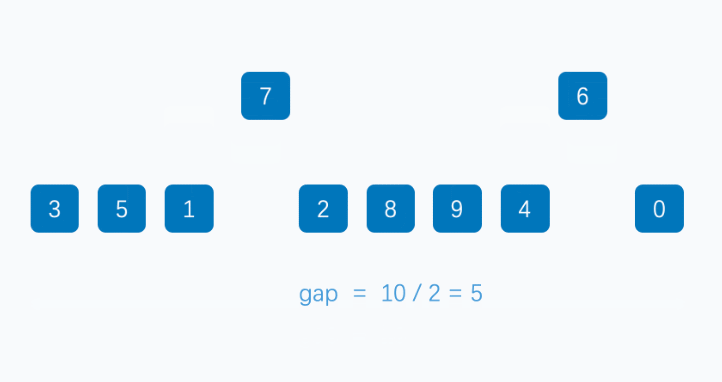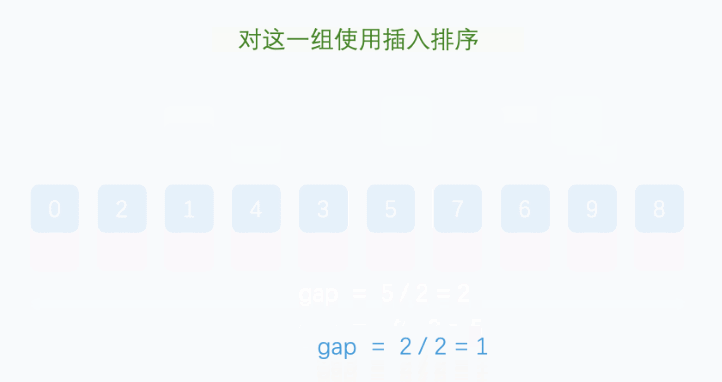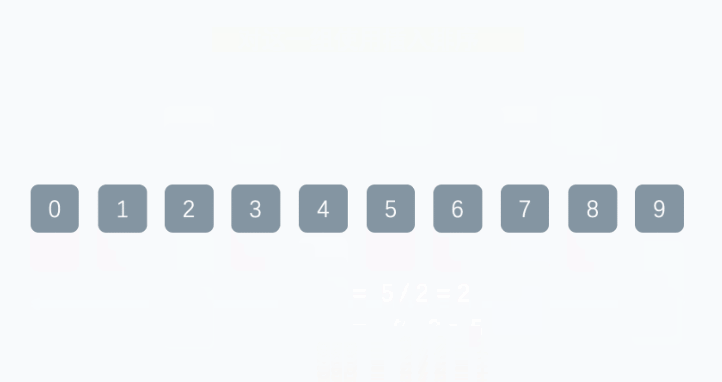
希尔排序的思想,就是使一个数组先部分有序,最后在全局有序。那么如何实现部分有序呢,我们可以对数组的元素按照某种规律进行分组,分组后,对组内的记录进行排序,如何重复进行分组和排序,当最终每组的成员只剩一个时,在进行排序的时候,就是使用了插入排序。

代码实现
我们定义了一个d变量,这个变量是用来进行分组的,当d大于0的时候,每次排序其实都是在预排序,也就是对分组内的成员进行排序,d是间隔,也就是将i,i+d,i+2*d...依次进行排序,之后,d/2或者d/3+1,按照某种规律,最终d=1的时候,在进行排序,就是进行了一次直接插入排序。
//2.希尔排序
void shellSort(int *a,int n){int i,j,d;for(d=n/2;d>=1;d=d/2){//分成不同的趟数,第一趟分割d=n/2for(i=d;i<n;i++){//对每一堂的每个小组排序if(a[i]<a[i-d]){int temp=a[i];for(j=i-d;j>=0&&a[j]>temp;j=j-d){a[j+d]=a[j];}a[j+d]=temp;}//of if}//of for2}//of for1
}算法分析
希尔排序的时间复杂度是一个复杂的问题,在Kunth所著的《计算机程序设计技巧》第3卷中,利用大量的实验统计资料得出,平均复杂度为O(N^1.25)到O(1.6 * N^1.25)。这里的就暂且不讨论该结果具体得出的方式。
希尔排序是否是稳定的算法呢?答案是不稳定的,因为我们在预排序的过程中,我们会进行大量的跳动式的移动元素的值,因此会导致不能按照原先的序列进行排序。
希尔排序中的d是如何取值的呢?当成Shell,也就是该算法的原作者,提出取d= d/2,然后向下取整,直到d=1时。后来Kunth提出取d= d/3 + 1 ,d/3向下取整的方式,直到gap=1时。这两种方式没有说哪个好,哪个坏,因此,使用其中一个即可。
3.冒泡排序
基本思想
冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列,依次比较两个元素,如果它们的顺序错误就把它们交换过来。如果遍历一遍数组,发现没有进行交换,故该数组已经有序,就不需要再进行排序。
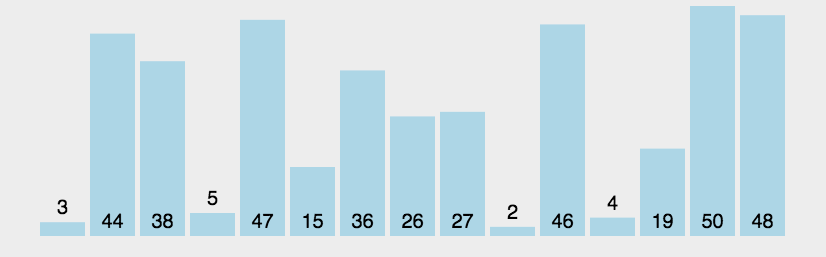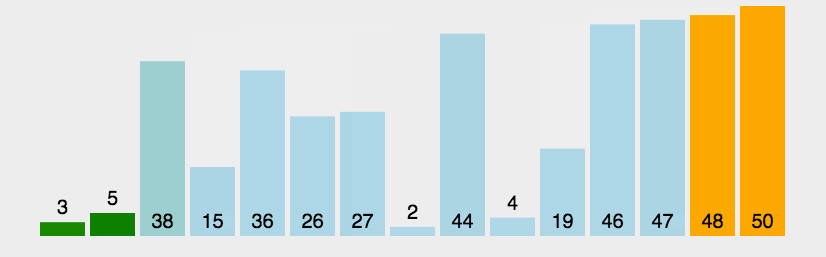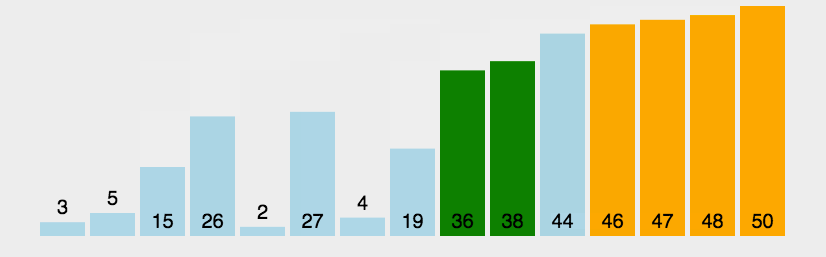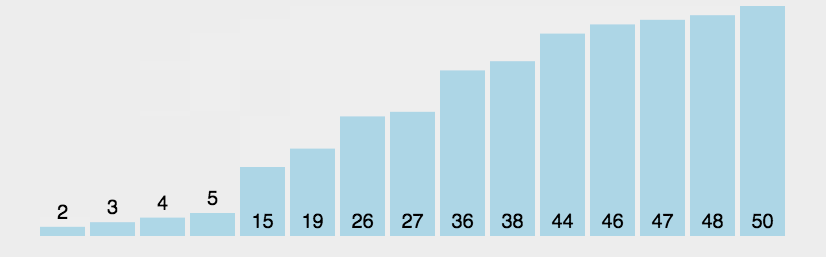
代码实现
该排序算法的代码实现也很简单,每趟排序,遍历一遍数组,两两比较,每一趟会将最小的值放在第一位。如果该趟排序没有元素交换,则不需要再进行排序了。
//3.冒泡排序
void BubbleSort(int *a,int n){for(int i=0;i<n;i++){//总共要冒n躺for(int j=0;j<n-i;j++){//每一趟比较前n-i个元素if(a[j]>a[j+1]){int temp=a[j];a[j]=a[j+1];a[j+1]=temp;}}}
}算法分析
时间复杂度,当元素为逆序时,需要进行n-1趟排序,而每趟需要比较n-1次。故最坏时间复杂度为O(N^2)。当元素为有序时,第一趟后,发现不需要交换元素,则只需要进行n-1次比较。故最好时间复杂度为O(N)。
空间也是仅使用了常数个辅助单元,故空间复杂度为O(1)。
冒泡排序是一种稳定的算法。
4.快速排序
基本思想
快速排序是Hoare于1962年提出的一种以二叉树结构的交换排序。
其本质是基于分治法实现的,基本思想是任取待排序元素序列中的某个元素作为基准,按照该排序码将待排序集合分割成两子序列,左子序列的所有元素均小于基准值,右子序列均大于基准值。然后左右子序列重复该操作,知道该序列有序为止。

代码实现
关于快速排序,其实c语言的<stdlib>库中自带快排函数qsort(),可以直接用,详情请看:
C语言学习--快速排序函数sqort()-CSDN博客
- 先将选定的基准值(最左边)直接取出,然后留下一个坑,
- 当右指针遇到小于基准值的数时,直接将该值放入坑中,而右指针指向的位置形成新的坑位,
- 然后左指针遇到大于基准值的数时,将该值放入坑中,左指针指向的位置形成坑位,
- 重复该步骤,直到左右指针相等。最后将基准值放入坑位之中。
- 之后也是以基准值为界限,递归排序基准值左右区间。

//4.快速排序
// 挖坑法
int PartSort(int* a, int begin, int end){int key = a[begin];int piti = begin;while (begin < end){// 右边找小,填到左边的坑里面去。这个位置形成新的坑while (begin < end && a[end] >= key){--end;}a[piti] = a[end];piti = end;// 左边找大,填到右边的坑里面去。这个位置形成新的坑while (begin < end && a[begin] <= key){++begin;}a[piti] = a[begin];piti = begin;}a[piti] = key;return piti;
}
// 快速排序递归实现
void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int keyi = PartSort(a, begin, end);// [begin, keyi-1] keyi [keyi+1, end]QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}算法分析
快速排序整体的综合性能与使用场景都是比较好的,所以才能称为快速排序。时间复杂度在优化后,基本上能达到O(N*logN),且优化后,优势更加明显。
空间复杂度,因为使用了递归,导致空间复杂度为O(logN)。
算法是不稳定的。
5.简单选择排序
基本思想
就是每一次从待排序的数据元素中选择最小或者最大的元素,放在序列的起始位置,直到全部排序完毕。
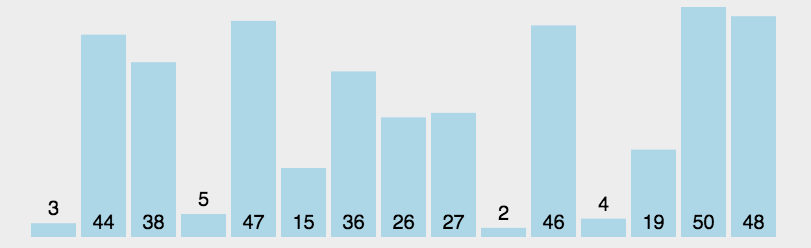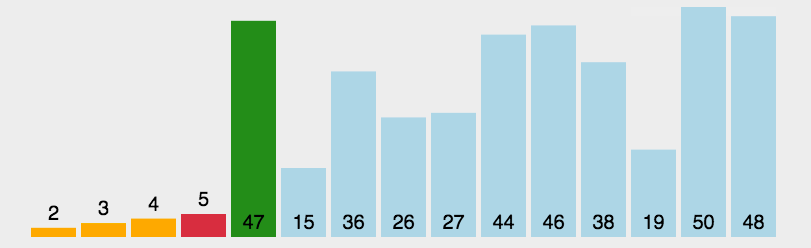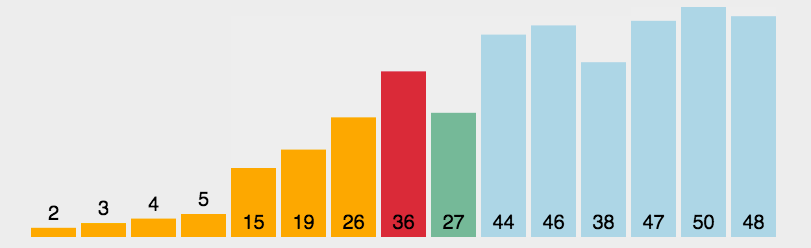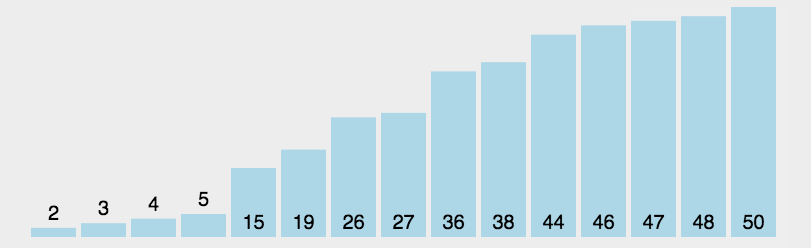
代码实现
//5.简单选择排序
void SelectSort(int *a,int n){for(int i=0;i<n-1;i++){//n-1躺,每一趟找一个最小值放到最前面int min=i;//记录最小值所在的下标便于交换位置for(int j=i+1;j<n;j++){if(a[j]<a[min]){min=j;}}//最小值所在下标minint temp=a[min];a[min]=a[i];a[i]=temp;//把每趟的最小值已到了最前面来}
}每次找到最小(最大)的值,记录当前的位置,并且与开始位置进行交换。然后重复进行该操作,直到集合中只剩一个元素为止。
算法分析
简单选择排序是比较简单的一种,但是效率并不高,无论是什么情况,算法时间复杂度都为O(N^2),因此,实际中很少使用。
空间复杂度为O(1),仅使用了常量级别的空间。
直接选择排序是否是稳定的算法呢?答案是不稳定的,在交换的过程中,可能会导致相对次序进行改变。比如,表L={2,2,1},经过第一趟排序后,结果为L={1,2,2},显示已经和原先的次序不一致,故该排序算法是不稳定的。
6.堆排序
后面三种,堆排序,归并排序,和基数排序不太好实现,我觉得理解原理就可以了;
基本思想
在了解堆排序之前,首先要知道堆这个数据结构。
堆是一颗完全二叉树,满足根节点大于或者小于左右孩子结点。堆可以分为大根堆和小根堆。大根堆的最大元素存放在根结点,任意一颗非根节点的值小于等于其双亲结点的值。而小根堆与大根堆恰好相反,小根堆的根元素为最小。
大根堆可以存放在一个数组中,节点下标i,对应的左右孩子分别是:2*i,2*i+1
那么,堆排序的思想很简单,首先在排序前,将待排序的数组构建成为一个堆,以大根堆为例,将堆顶元素与堆底元素进行交换,然后继续将堆顶元素进行向下调整,然后保持大根堆的特性。因为对顶元素永远是当前堆中最大的一个,将其放在最后,就相当于把最大元素放在了数组的最后,再将堆的范围缩小,因此大根堆排序后的结果为升序。
代码实现
//6.堆排序
void swap(int* p1, int* p2){int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
// 堆排序
// 向下取整
void AdjustDwon(int* a, int n, int root){int child = root * 2 + 1;while (child < n){if (child + 1 < n && a[child + 1] > a[child]){child++;}if (a[child] > a[root]){swap(&a[child], &a[root]);root = child;child = root * 2 + 1;}else{break;}}
}
void HeapSort(int* a, int n){// 建堆方式2:O(N)for (int i = (n-2) / 2; i >= 0; --i){AdjustDwon(a, n, i);}// O(N*logN)int end = n - 1;while (end > 0){swap(&a[0], &a[end]);AdjustDwon(a, end, 0);--end;}
}
算法分析
堆排序是一种效率很高的排序,通过使用堆的数据结构来进行排序,时间复杂度为O(N*logN),建堆的时间为O(N),然后有n-1次向下调整操作,每次调整的时间复杂度与高度有关,而h=log2n + 1,故时间复杂度为O(N*logN)。
空间也是仅使用了常数个辅助单元,故空间复杂的为O(1)。
堆排序是否是稳定的算法呢?答案是不稳定的,在进行筛选的过程中,可能把后面相同的元素调整到前面来。
7.归并排序
基本思想
归并排序是建立在归并操作上的一种有效的排序算法,该算法采用的是分治法。其思想就是将序列分成n个子序列,再使用子序列有序,之后,将其合并为一个新的有序表,如果两个有序表合并为一个有序表,称为二路归并。
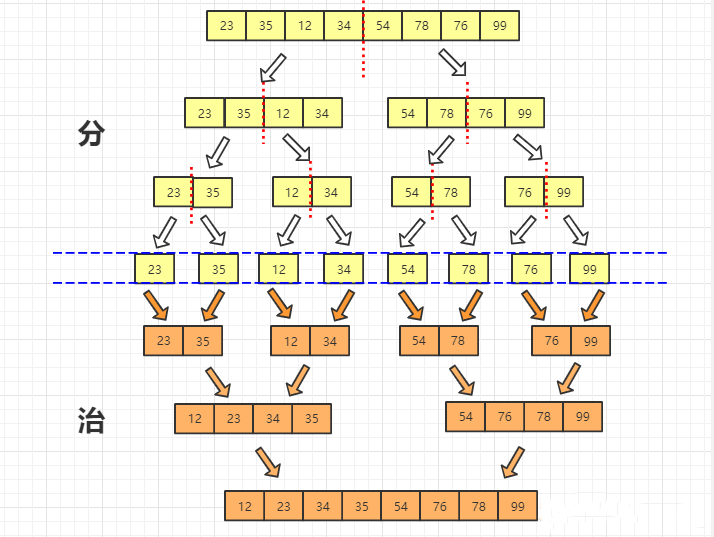
代码实现
//7.归并排序
void _MergeSort(int* a, int begin, int end, int* tmp){int mid = (begin + end) / 2;// [begin, mid] [mid+1, end] 分治递归,让子区间有序_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid + 1, end, tmp);//归并 [begin, mid] [mid+1, end]int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int i = begin1;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}// 把归并数据拷贝回原数组memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}
void MergeSort(int* a, int n){// 借助一个新的辅助空间来帮助合并int* tmp = (int*)malloc(sizeof(int) * n);_MergeSort(a, 0, n - 1, tmp);free(tmp);
}算法分析
归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
每趟归并的时间为O(N),并且需要log2N趟归并,所以时间复杂度为O(N*logN)。
二路归并排序不会改变相同关键字记录的相对次序,因此是一种稳定的算法。
8.基数排序
基本思想
- 将所有待比较数值统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。
- 这样说明,比较难理解,下面我们看一个图文解释,理解基数排序的步骤

注意:基数排序中不能出现负数!!!
代码实现
//8.基数排序
//基数排序
void RadixSort(int* arr, int n){//max为数组中最大值int max = arr[0];int base = 1;//找出数组中的最大值for (int i = 0; i < n; i++){if (arr[i] > max){max = arr[i];}}//循环结束max就是数组最大值//临时存放数组元素的空间int* tmp = (int*)malloc(sizeof(int)*n);//循环次数为最大数的位数while (max / base > 0){ //定义十个桶,桶里面装的不是数据本身,而是每一轮排序对应(十、白、千...)位的个数//统计每个桶里面装几个数int bucket[10] = { 0 };for (int i = 0; i < n; i++){//arr[i] / base % 10可以取到个位、十位、百位对应的数字bucket[arr[i] / base % 10]++;}//循环结束就已经统计好了本轮每个桶里面应该装几个数//将桶里面的元素依次累加起来,就可以知道元素存放在临时数组中的位置for (int i = 1; i < 10; i++){bucket[i] += bucket[i - 1];}//循环结束现在桶中就存放的是每个元素应该存放到临时数组的位置//开始放数到临时数组tmpfor (int i = n - 1; i >= 0; i--){tmp[bucket[arr[i] / base % 10] - 1] = arr[i];bucket[arr[i] / base % 10]--;}//不能从前往后放,因为这样会导致十位排好了个位又乱了,百位排好了十位又乱了/*for (int i = 0; i < n; i++){tmp[bucket[arr[i] / base % 10] - 1] = arr[i];bucket[arr[i] / base % 10]--;}*///把临时数组里面的数拷贝回去for (int i = 0; i < n; i++){arr[i] = tmp[i];}base *= 10;}free(tmp);
}
算法分析
基数排序的时间复杂度跟基数选取有关,平均复杂度为O(k·n)。基数排序为稳定排序算法。

总结
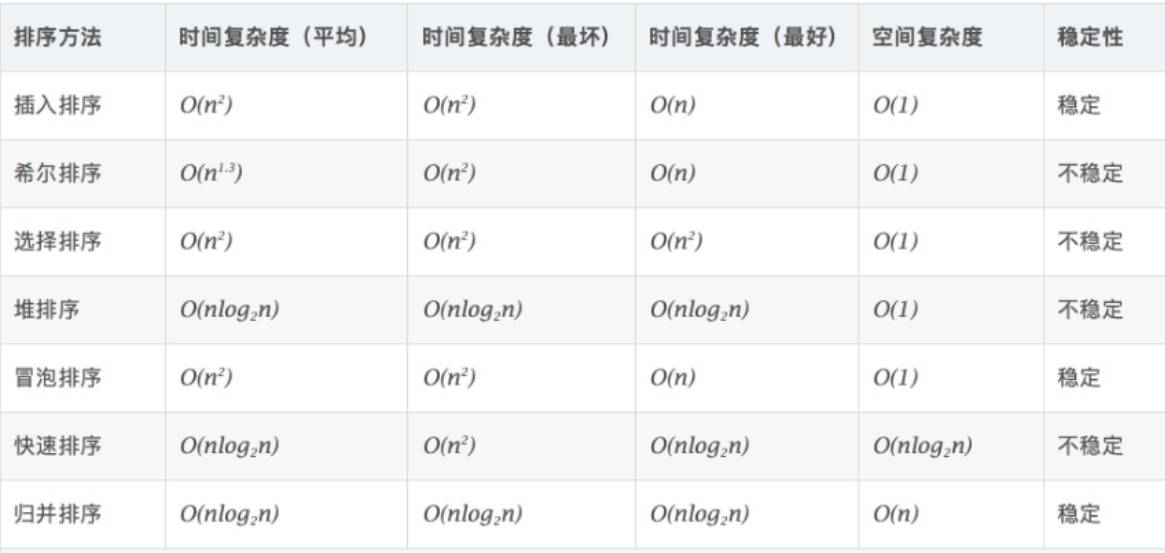
相关文章:

C语言学习--八种排序算法
目录 排序的概念 1.直接插入排序 基本思想 代码实现 算法分析 2.希尔排序 基本思想 代码实现 算法分析 3.冒泡排序 基本思想 代码实现 算法分析 4.快速排序 基本思想 代码实现 算法分析 5.简单选择排序 基本思想 代码实现 算法分析 6.堆排序 基本思想 代…...
Infineon_TC264智能车代码初探及C语言深度学习(二)
本篇文章记录我在智能车竞赛中,对 Infineon_TC264 这款芯片的底层库函数的学习分析。通过深入地对其库函数进行分析,C语言深入的知识得以再次在编程中呈现和运用。故觉得很有必要在此进行记录分享一下。 目录 编辑 一、代码段分析 NO.1 指向结构体…...

第十三届蓝桥杯(C/C++ 大学B组)
目录 试题 A: 九进制转十进制 试题 B: 顺子日期 试题 C: 刷题统计 试题 D: 修剪灌木 试题 E: X 进制减法 试题 F: 统计子矩阵 试题 G: 积木画 试题 H: 扫雷 试题 I: 李白打酒加强版 试题 J: 砍竹子 试题 A: 九进制转十进制 九进制正整数 ( 2022 )转换成十进制等于多…...
数据结构从入门到精通——排序的概念及运用
排序的概念及运用 前言一、排序的概念排序稳定性内部排序外部排序 二、排序运用三、常见的排序算法四、排序性能检测代码srand()clock() 五、oj排序测试代码 前言 排序是将数据按照一定规则重新排列的过程,常见规则有升序、降序等。排序算法如冒泡排序、快速排序等…...
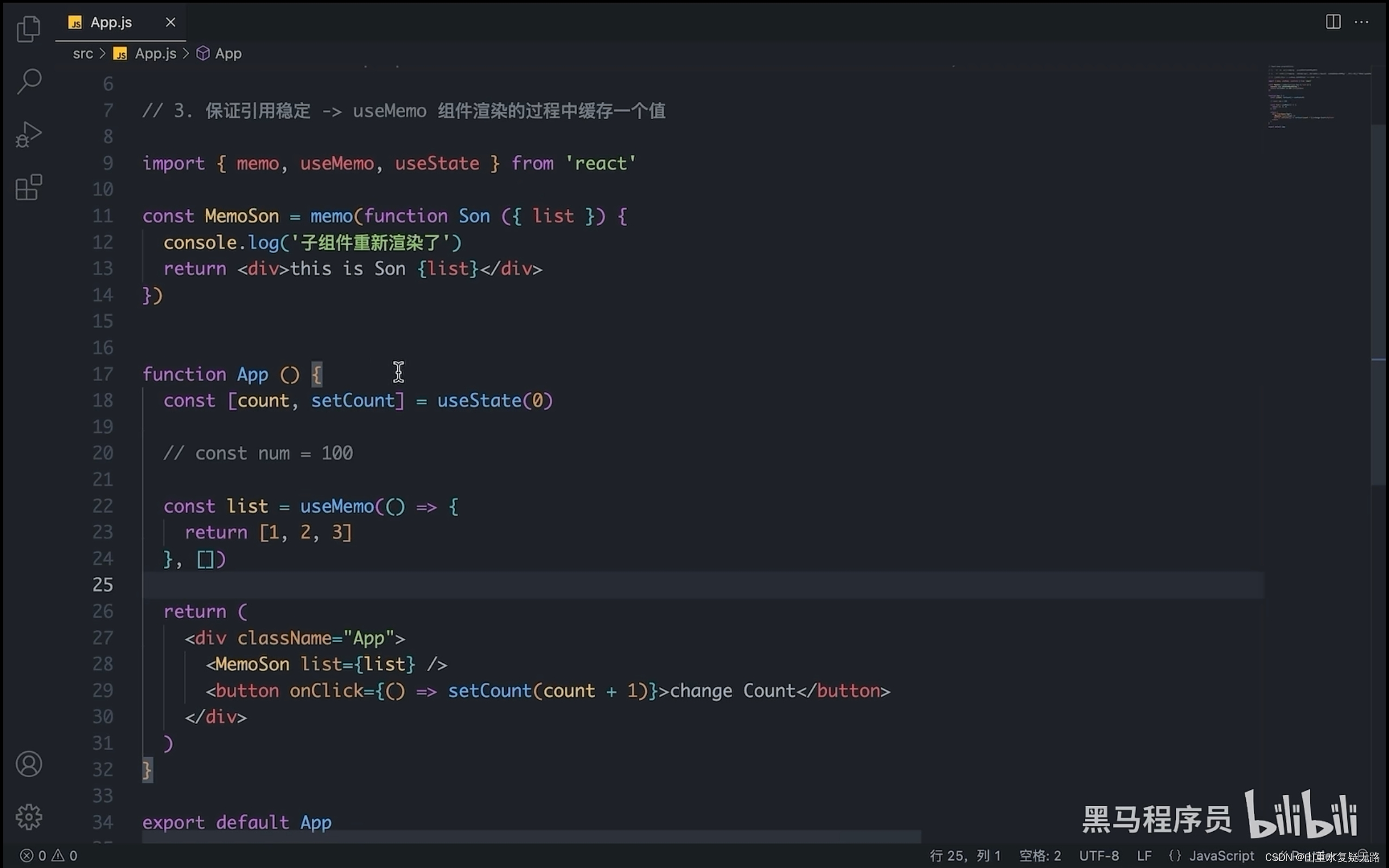
react面试题总结
1、当调用 setState的时候,发生了什么操作? 当调用 setState时, React做的第一件事是将传递给setState的对象合并到组件的当前状态,这将启动一个称为和解( reconciliation)的过程。 和解的最终目标是&#…...
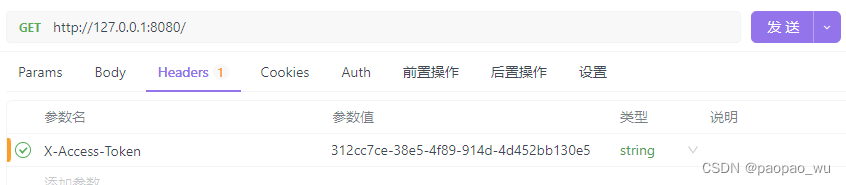
5_springboot_shiro_jwt_多端认证鉴权_禁用Cookie
1. Cookie是什么 Cookie是一种在客户端(通常是用户的Web浏览器)和服务器之间进行状态管理的技术。当用户访问Web服务器时,服务器可以向用户的浏览器发送一个名为Cookie的小数据块。浏览器会将这个Cookie存储在客户端,为这个Co…...

条形码申请指南:外地人如何成功注册香港条形码
香港条形码是打造的通行证,消费者对香港条码有一定的认知,拥有香港条形码就获得消费者对产品的认可,香港条形码是全球条码中具有防伪功能的条形码,化妆品、护肤品、保健品、包装食品等行业的产品认证,就有必要申请香港…...

Covalent Network借助大规模的历史Web3数据集,推动人工智能发展
人工智能在众多领域中增强了区块链的实用性,反之亦然,区块链确保了 AI 模型所使用的数据的来源和质量。人工智能带来的生产力提升,将与区块链系统固有的安全性和透明度融合。 Covalent Network(CQT)正位于这两项互补技…...

test测试类-变量学习
test测试类 作用:标记到类上成为测试类,标记到方法上成为测试方法 变量:测试类的变量,在测试类括号中应用 1、invocationCount变量 意思是这个方法应该被调用的次数。 在测试框架中,特别是当使用参数化测试或数据驱动…...

【DL经典回顾】激活函数大汇总(二十七)(Bent Identity附代码和详细公式)
激活函数大汇总(二十七)(Bent Identity附代码和详细公式) 更多激活函数见激活函数大汇总列表 一、引言 欢迎来到我们深入探索神经网络核心组成部分——激活函数的系列博客。在人工智能的世界里,激活函数扮演着不可或…...

element-plus el-table表格默认选中某一行
需求:进入页面时默认选中表格第一行 <el-tableref"singleTableRef":data"tableData"highlight-current-rowrow-click"handleCurrentChange" ><el-table-column property"date" label"日期" /><…...

Vue+SpringBoot打造民宿预定管理系统
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 用例设计2.2 功能设计2.2.1 租客角色2.2.2 房主角色2.2.3 系统管理员角色 三、系统展示四、核心代码4.1 查询民宿4.2 新增民宿4.3 新增民宿评价4.4 查询留言4.5 新增民宿订单 五、免责说明 一、摘要 1.1 项目介绍 基于…...
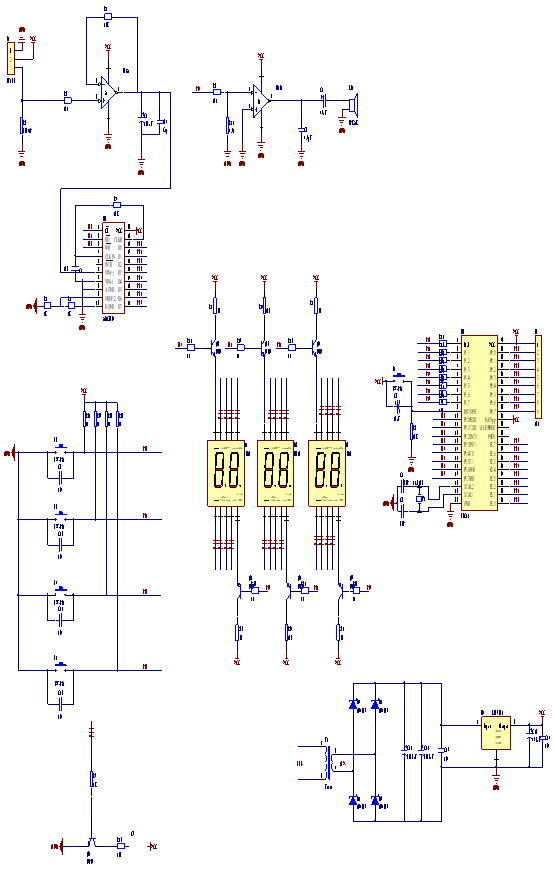
基于单片机的模糊PID炉温控制系统设计
摘 要 电热炉是在工业热处理的生产中广泛使用的一种设备,电热炉的温度控制系统存在时变性,非线性,滞后性等特征,难以用常规PID的控制器对系统达到很好的控制效果。当控温精度的要求高时,使用传统的控制理论方法难以达…...

深入浅出落地应用分析:AI数字人「微软小冰」
hi,各位,今天要聊的是AI小冰,机缘巧合,投递了这家公司的产品,正好最近在看数字人相关的,就详细剖析下这款产品! 前言 小冰,全称为北京红棉小冰科技有限公司,前身为微软(亚洲)互联网工程院人工智能小冰团队,是微软全球最大的人工智能独立产品研发团队。作为微软全…...

【早鸟优惠|高录用|EI稳定检索】2024年虚拟现实、图像和信号处理国际学术会议(ICVISP 2024)诚邀投稿/参会!
【早鸟优惠|高录用|EI稳定检索】 2024年虚拟现实、图像和信号处理国际学术会议(ICVISP 2024)诚邀投稿/参会! # 早鸟优惠 # 先投稿先送审 # #投稿免费参会、口头汇报及海报展示# 2024年虚拟现实、图像和信号处理国际学术会议(I…...

CPU设计实战—异常处理指令
异常类型以及精确异常的处理 异常有点像中断,处理完还要回到原来的状态,所以需要对之前的状态进行保存。本CPU主要实现对以下异常的处理: 1.外部硬件中断 2.复位异常 3.系统调用异常(发生在译码阶段) 4.溢出异常&…...
 match_phrase的使用)
Elasticsearch(13) match_phrase的使用
elasticsearch version: 7.10.1 match_phrase 语法 POST <index>/_search {"query": {"match_phrase": {"<field_name>": {"query": "<your_search_phrase>","slop": <max_dis…...

通过路由器监控,优化网络效率
路由器是网络的基本连接组件,路由器监控涉及将路由器网络作为一个整体进行管理,其中持续监控路由器的性能、运行状况、安全性和可用性,以确保更好的操作和最短的停机时间,因此监控路由器至关重要。 为什么路由器监控对组织很重要…...

使用canvas实现图纸标记及回显
图纸 图纸标记后的效果图 最近做的一个qms项目里面,需要前端在图纸上实现标记及标记后的内容还要能够回显,然后后端通过标记的点,去读取标记图纸的内容,如一些公式、数据之类的,目前实现的功能有 在图纸上面进行矩形…...

鸿蒙-自定义组件的生命周期
目录 自定义组件的生命周期 1.aboutToAppear 2.aboutToDisappear 3.onPageShow 4.onPageHide 5.onBackPress 日志输出 1.显示页面 2.页面点击返回按钮 3.页面跳转 4.页面返回 自定义组件的生命周期 先来一段列子 import router from ohos.router Entry Component…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

