【C++】用红黑树模拟实现set、map
目录
- 前言及准备:
- 一、红黑树接口
- 1.1 begin
- 1.2 end
- 1.3 查找
- 1.4 插入
- 1.5 左单旋和右单旋
- 二、树形迭代器(正向)
- 2.1 前置++
- 三、模拟实现set
- 四、模拟实现map
前言及准备:
set、map的底层结构是红黑树,它们的函数通过调用红黑树的接口来实现,红黑树一些接口需要通过树形迭代器来实现。set是k模型,map是kv模型,红黑树要不要写两份呢?答案是不需要,只用一份即可,通过仿函数来控制。
定义树的节点:
template<class T>
struct RBTreeNode
{RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;T _data;Colour _col;RBTreeNode(const T& data):_left(nullptr),_right(nullptr),_parent(nullptr),_data(data),_col(RED){}
};
红黑树有3个指针域,数据域用T来表示,如果是set,那么传过来的是k模型;如果是map,是kv模型。新增的节点的颜色默认是红色(根节点除外)。
一、红黑树接口
1.1 begin
返回的是红黑树的第一个节点,注意,这里的第一个的顺序是按中序遍历来的,所以,第一个节点的位置是树的最左节点。
//返回的迭代器指向的数据可修改
iterator begin()
{Node* subLeft = _root;while (subLeft->_left){subLeft = subLeft->_left;}return iterator(subLeft);
}
//返回的迭代器指向的数据不可修改
const_iterator begin() const
{Node* subLeft = _root;while (subLeft->_left){subLeft = subLeft->_left;}return const_iterator(subLeft);
}
1.2 end
返回的是最后一个节点(最右侧节点)的下一个位置。由于这里实现的红黑树没有头节点,所以只能给nullptr来勉强实现这个迭代器。但是这样其实是不行的,因为对end()位置的迭代器进行 - - 操作,必须要能找最后一个元素,给nullptr就找不到了。如果有头节点,那么end()的位置应该是在头节点的位置。
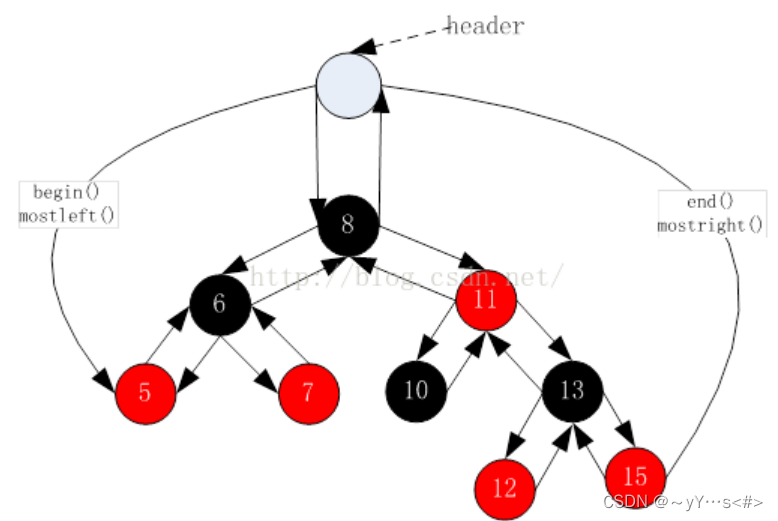
iterator end()
{return iterator(nullptr);
}
const_iterator end() const
{return const_iterator(nullptr);
}
1.3 查找
查找的过程与之前写的二叉搜索树没有多大区别,要注意的是返回类型,找到了,返回的是该节点的迭代器,找不到就返回end()。
iterator Find(const K& key)
{KeyOfT kot;Node* cur = _root;while (cur){if (kot(cur->_data) < key){cur = cur->_right;}else if (kot(cur->_data) > key){cur = cur->_left;}else{return iterator(cur);}}return end();
}
咋知道是set还是map的数据进行比较,看传过来的类模板参数中的仿函数是set的还是map的。当然,这里只需写好就行,不用关心传过来的是什么,set和map的仿函数内部已经确定好了。
说明一下:
template<class K, class T, class KeyOfT>
这是该红黑树的类模板,K是Find()函数中要对比的数据类型,T是节点的数据域,可能是k模型,也有可能是kv模型。怎么确定呢?通过第三个类模板参数——仿函数来确定。仿函数传的是set的,就是k模型;仿函数传的是map的,就是kv模型。仿函数内部具体实现下面再说。
1.4 插入
为了接近STL库中的insert函数,返回类型是pair,即插入成功,返回该节点的迭代器和true;插入失败,说明该节点已经存在,返回该节点的迭代器和false。
pair<iterator, bool> Insert(const T& data)
{//为空if (_root == nullptr){_root = new Node(data);_root->_col = BLACK;//根节点都是黑色的,特殊处理return make_pair(iterator(_root), true);}//非空KeyOfT kot;Node* cur = _root;Node* parent = nullptr;while (cur){if (kot(cur->_data) < kot(data)){parent = cur;cur = cur->_right;}else if (kot(cur->_data) > kot(data)){parent = cur;cur = cur->_left;}else{return make_pair(iterator(cur), false);}}//插入新节点cur = new Node(data);//红色的if (kot(parent->_data) < kot(data)){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;Node* newnode = cur;//调整颜色while (parent && parent->_col == RED){Node* grandfather = parent->_parent;//爷爷节点//父节点在爷爷节点的左边,那么叔叔节点在右边if (parent == grandfather->_left){Node* uncle = grandfather->_right;//情况一:叔叔存在且为红if (uncle && uncle->_col == RED){grandfather->_col = RED;uncle->_col = parent->_col = BLACK;cur = grandfather;//爷爷不是根,向上更新parent = cur->_parent;}//情况二:叔叔不存在/存在且为黑else{//单旋if (cur == parent->_left){RotateR(grandfather);//右单旋parent->_col = BLACK;//变色grandfather->_col = RED;}//左右双旋 // cur == parent->_rightelse{RotateL(parent);//先左单旋RotateR(grandfather);//再右单旋grandfather->_col = RED;//变色cur->_col = BLACK;}}}else//父节点在右边,叔叔在左边{Node* uncle = grandfather->_left;//情况一:叔叔存在且为红if (uncle && uncle->_col == RED){grandfather->_col = RED;uncle->_col = parent->_col = BLACK;cur = grandfather;//爷爷不是根,向上更新parent = cur->_parent;}//情况二:叔叔不存在/存在且为黑else{//单旋if (cur == parent->_right){RotateL(grandfather);//左单旋parent->_col = BLACK;//变色grandfather->_col = RED;}//右左双旋 // cur == parent->_leftelse{RotateR(parent);//先右单旋RotateL(grandfather);//再左单旋grandfather->_col = RED;//变色cur->_col = BLACK;}break;//经过情况二后跳出}}}_root->_col = BLACK;//统一处理,根必须是黑的return make_pair(iterator(newnode), true);
}
1.5 左单旋和右单旋
这两个就是之前的,这里不作重复叙述了
//左单旋
void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;//不为空if (subRL){subRL->_parent = parent;}subR->_left = parent;Node* ppnode = parent->_parent;parent->_parent = subR;//处理parent如果为根if (parent == _root){_root = subR;subR->_parent = nullptr;}//不为根,处理与ppnode的连接else{if (ppnode->_left == parent){ppnode->_left = subR;}else{ppnode->_right = subR;}subR->_parent = ppnode;}
}//右单旋
void RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;//不为空if (subLR){subLR->_parent = parent;}subL->_right = parent;Node* ppnode = parent->_parent;parent->_parent = subL;if (parent == _root){_root = subL;subL->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subL;}else{ppnode->_right = subL;}subL->_parent = ppnode;}
}
二、树形迭代器(正向)
2.1 前置++
首先要清楚的是++到下一个节点位置是按中序遍历走的,主要有两种情况:
- 该节点有右子树
- 该节点没有右子树
1️⃣有右子树
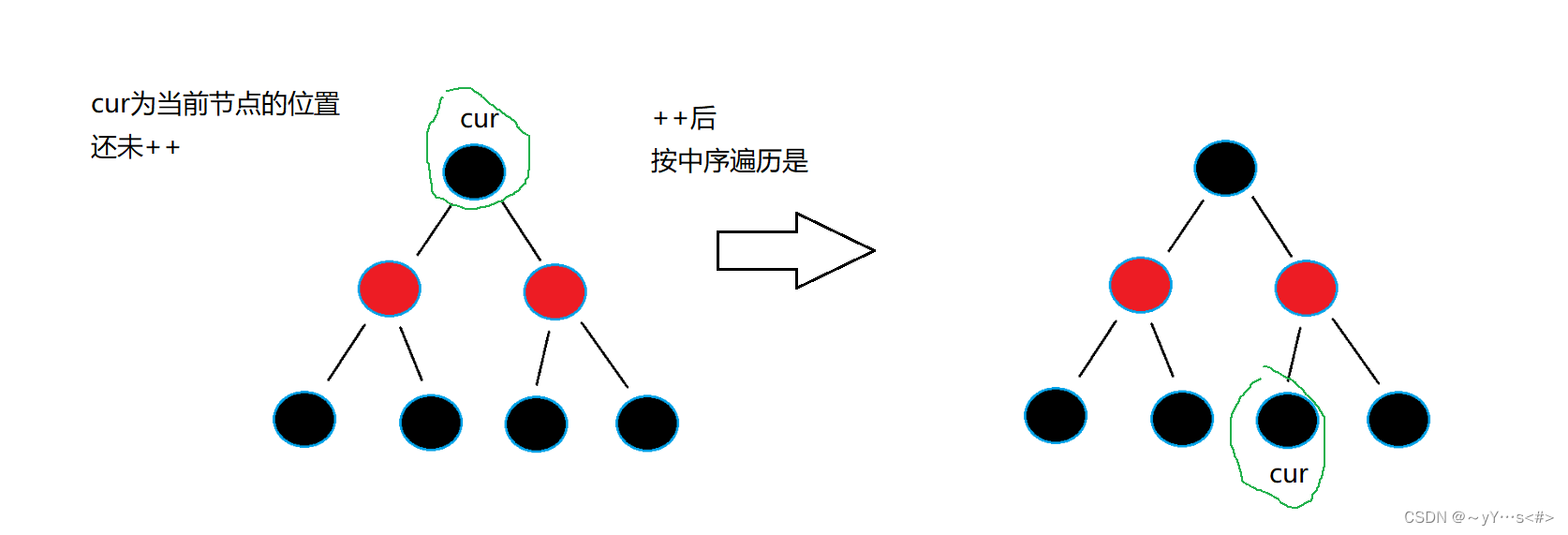
总结:有右子树++后的下一个节点是右子树的最左节点
2️⃣没有右子树
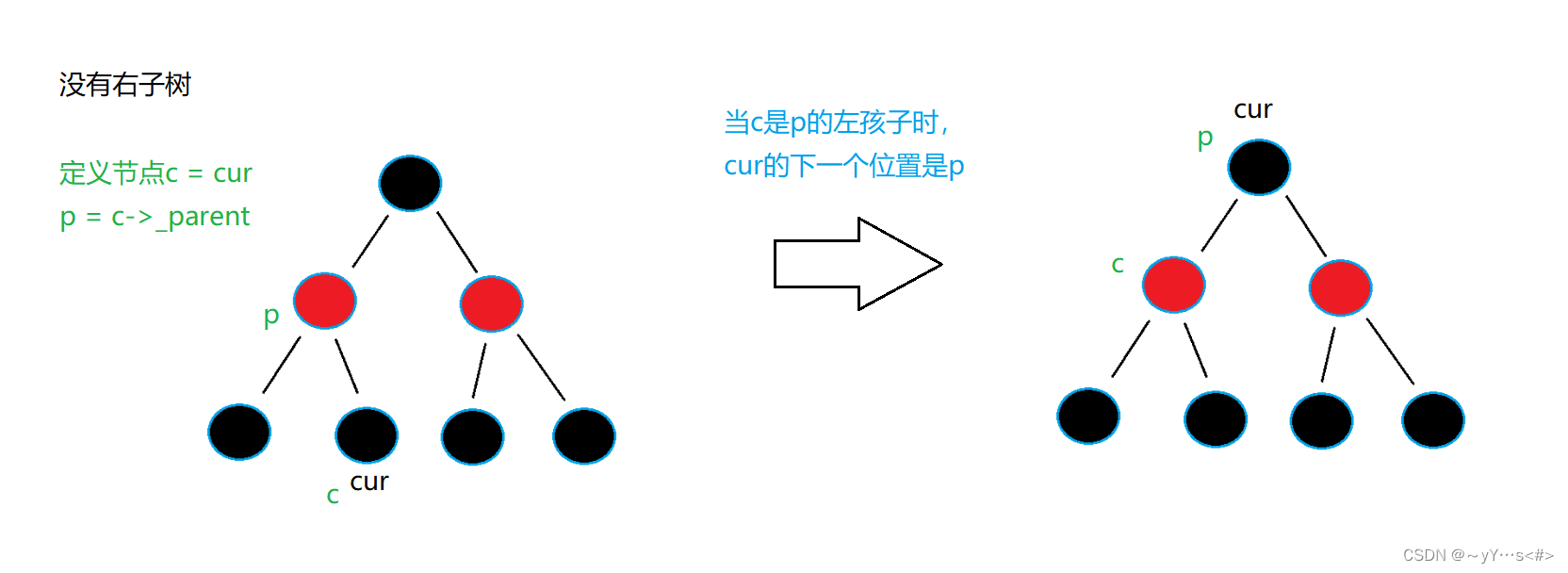
总结:没有右子树++后下一个节点是祖先节点中左孩子是当前节点(原来节点的位置)或者左孩子是当前节点的父亲的那个祖先
有点弯,再来图捋一捋:
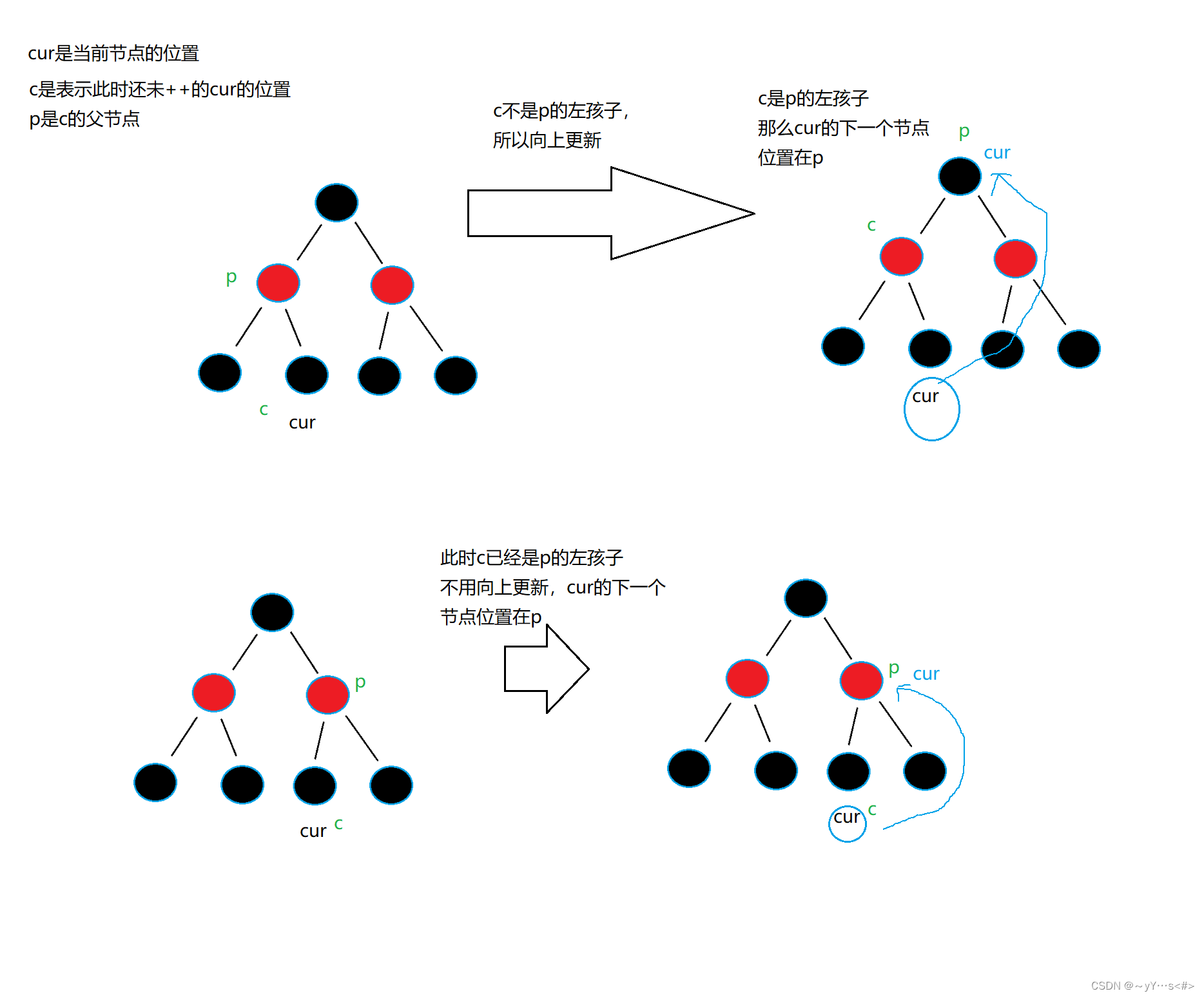
前置- -的逻辑与前置++刚好相反
template<class T, class Ref, class Ptr>
struct RBTreeIterator
{typedef RBTreeNode<T> Node;typedef RBTreeIterator<T, Ref, Ptr> Self;Node* _node;RBTreeIterator(Node* node):_node(node){}Ref operator*(){return _node->_data;}Ptr operator->(){return &_node->_data;}//前置++Self& operator++(){//右子树存在if (_node->_right){//下一个节点在右子树的最左边Node* subLeft = _node->_right;while (subLeft->_left){subLeft = subLeft->_left;}_node = subLeft;}//右子树不存在else{Node* cur = _node;Node* parent = cur->_parent;//cur是parent的左子树,parent就是下一个while (parent && parent->_right == cur){cur = parent;parent = parent->_parent;}_node = parent;}return *this;}//前置--Self& operator--()//与前置++的逻辑相反{//左子树存在if (_node->_left){//下一个节点是左子树的最右一个Node* subRight = _node->_left;while (subRight->_right){subRight = subRight->_right;}_node = subRight;}//左子树不存在else{Node* cur = _node;Node* parent = cur->_parent;//cur是parent的右子树时parent就是下一个while (parent && parent->_left == cur){cur = parent;parent = parent->_parent;}_node = parent;}return *this;}bool operator!=(const Self& s){ return _node != s._node;}bool operator==(const Self& s){return _node == s._node;}
};
三、模拟实现set
set是k模型,仿函数返回的只有key值。其他接口调用红黑树的
template<class K>
class set
{//仿函数struct SetKeyOfT{const K& operator()(const K& key){return key;}};
public:typedef typename RBTree<K, const K, SetKeyOfT>::iterator iterator;typedef typename RBTree<K, const K, SetKeyOfT>::const_iterator const_iterator;//迭代器iterator begin(){return _t.begin();}const_iterator begin() const{return _t.begin();}iterator end(){return _t.end();}const_iterator end() const{return _t.end();}//插入pair<iterator, bool> Insert(const K& key){return _t.Insert(key);}//查找iterator Find(const K& key){_t.Find(key);}
private:RBTree<K, const K, SetKeyOfT> _t;
};
四、模拟实现map
map是kv模型,仿函数返回的取kv中的key值。其他接口调用红黑树的,除此之外,多了一个operator[]
template<class K, class V>
class map
{struct MapKeyOfT{const K& operator()(const pair<K, V>& kv){return kv.first;}};public:typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::iterator iterator;typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::const_iterator const_iterator;//迭代器iterator begin(){return _t.begin();}const_iterator begin() const{return _t.begin();}iterator end(){return _t.end();}const_iterator end() const{return _t.end();}//插入pair<iterator, bool> Insert(const pair<K, V>& kv){return _t.Insert(kv);}//查找iterator Find(const K& key){_t.Find(key);}//operator[]V& operator[](const K& key){pair<iterator, bool> ret = Insert(make_pair(key, V()));return ret.first->second;}
private:RBTree<K, pair<const K, V>, MapKeyOfT> _t;
};
相关文章:

【C++】用红黑树模拟实现set、map
目录 前言及准备:一、红黑树接口1.1 begin1.2 end1.3 查找1.4 插入1.5 左单旋和右单旋 二、树形迭代器(正向)2.1 前置 三、模拟实现set四、模拟实现map 前言及准备: set、map的底层结构是红黑树,它们的函数通过调用红…...

实现:mysql-5.7.42 到 mysql-8.2.0 的升级(二进制方式)
实现:mysql-5.7.42 到 mysql-8.2.0 的升级(二进制方式) 1、操作环境1、查看当前数据库版本2、操作系统版本3、查看 Linux 系统上的 glibc(GNU C 库)版本(**这里很重要,要下载对应的内核mysql版本…...

深入探讨医保购药APP的技术架构与设计思路
随着移动互联网的发展,医疗保健行业也迎来了数字化转型的浪潮。医保购药APP作为医保体系数字化的一部分,其技术架构和设计思路至关重要。接下来,小编将为您讲解医保购药APP的技术架构与设计思路,为相关从业者提供参考和启发。 一、…...

react中点击按钮不能获取最新的state时候
在这个问题中,用户希望在点击确认按钮时触发handleChange函数,并且能够正确获取到最新的bzText值。最初的代码中,在handleOpen函数中弹出一个确认框,并在确认框的onOk回调函数中调用handleChange函数。然而,由于组件传…...
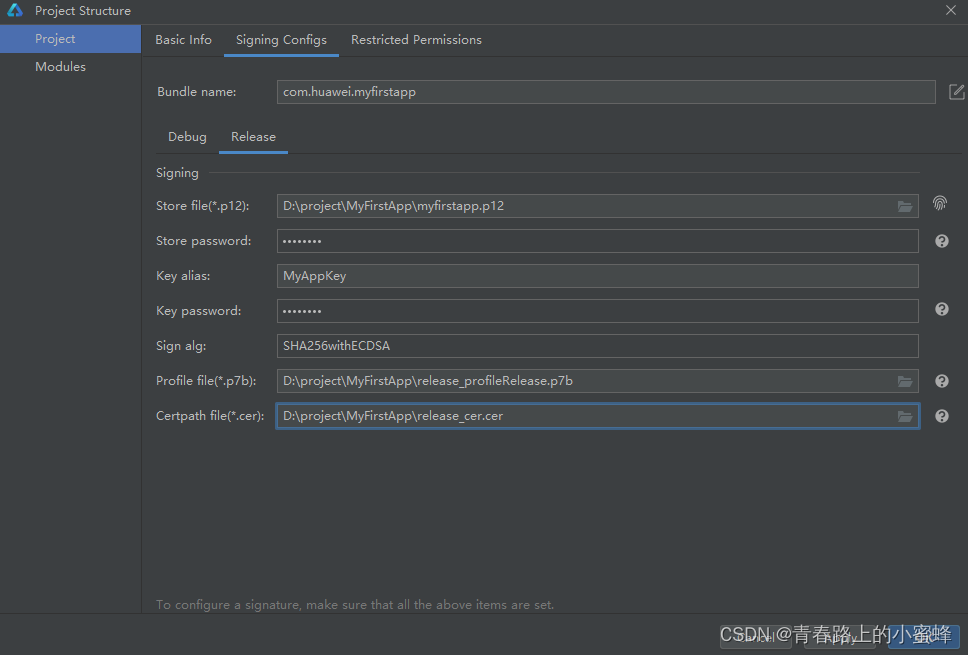
2、鸿蒙学习-申请调试证书和调试Profile文件
申请发布证书 发布证书由AGC颁发的、为HarmonyOS应用配置签名信息的数字证书,可保障软件代码完整性和发布者身份真实性。证书格式为.cer,包含公钥、证书指纹等信息。 说明 请确保您的开发者帐号已实名认证。每个帐号最多申请1个发布证书。 1、登录AppGa…...
:十大排序算法(希尔排序) (快速排序)c语言版)
蓝桥杯算法基础(13):十大排序算法(希尔排序) (快速排序)c语言版
希尔排序 优化版的插入排序,优化的地方就是步长(增量)增大了,原来的插入排序的步长(增量)是1,而希尔排序的步长(增量)可以很大,然后逐渐减小直到1形成插入排…...
)
web学习笔记(三十二)
目录 1.函数的call、apply、bind方法 1.1call、apply、bind的相同点 1.2call、apply、bind的不同点 1.3call、apply、bind的使用场景 2. 对象的深拷贝 2.1对象的浅拷贝 2.1对象的深拷贝 1.函数的call、apply、bind方法 1.1call、apply、bind的相同点 在没有传参数时&…...

Android 地图SDK 绘制点 删除 指定
问题 Android 地图SDK 删除指定绘制点 详细问题 笔者进行Android 项目开发,对于已标记的绘制点,提供撤回按钮,即删除绘制点,如何实现。 解决方案 新增绘制点 private List<Marker> markerList new ArrayList<>…...
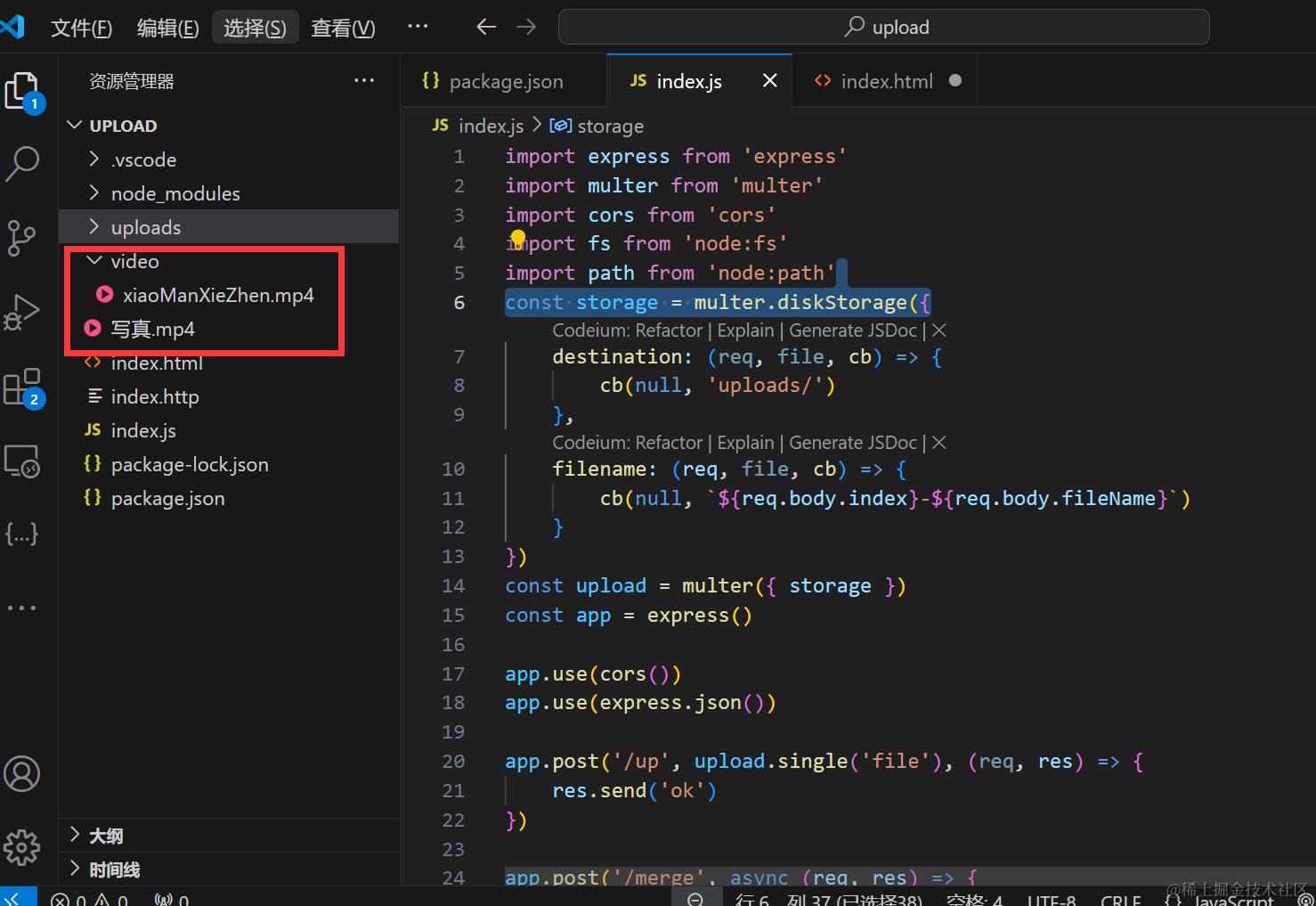
Nodejs 第五十八章(大文件上传)
在现代网站中,越来越多的个性化图片,视频,去展示,因此我们的网站一般都会支持文件上传。 文件上传的方案 大文件上传:将大文件切分成较小的片段(通常称为分片或块),然后逐个上传这…...
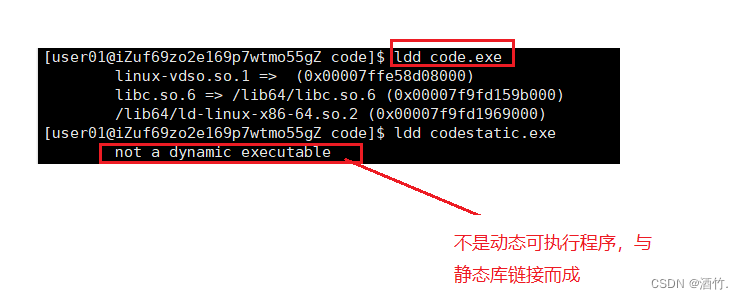
Linux编译器--gcc/g++的使用
1. gcc与g gcc与g分别是c语言与c代码的编译器,但同时g也兼容c语言。 我们知道在Linux中,系统并不以文件后缀来区分文件类别。但对于gcc与g等编译器而言却是需要的。Linux中c代码文件的后缀是.c,c代码文件的后缀是.cpp(.cc)(.cxx)。 在Linu…...

苍穹外卖-day13:vue基础回顾+进阶
vue基础回顾进阶 课程内容 VUE 基础回顾路由 Vue-Router状态管理 vuexTypeScript 1. VUE 基础回顾 1.1 基于脚手架创建前端工程 1.1.1 环境要求 要想基于脚手架创建前端工程,需要具备如下环境要求: node.js 前端项目的运行环境 学习web阶段已安…...

蓝桥杯/慈善晚会/c\c++
问题描述 热心公益的G哥哥又来举办慈善晚会了,这次他邀请到了巴菲特、马云等巨富,还邀请到了大V、小C等算法界泰斗。晚会一共邀请了n位尊贵的客人,每位客人都位于不同的城市,也就是说每座城市都有且仅有一位客人。这些城市的编号为…...
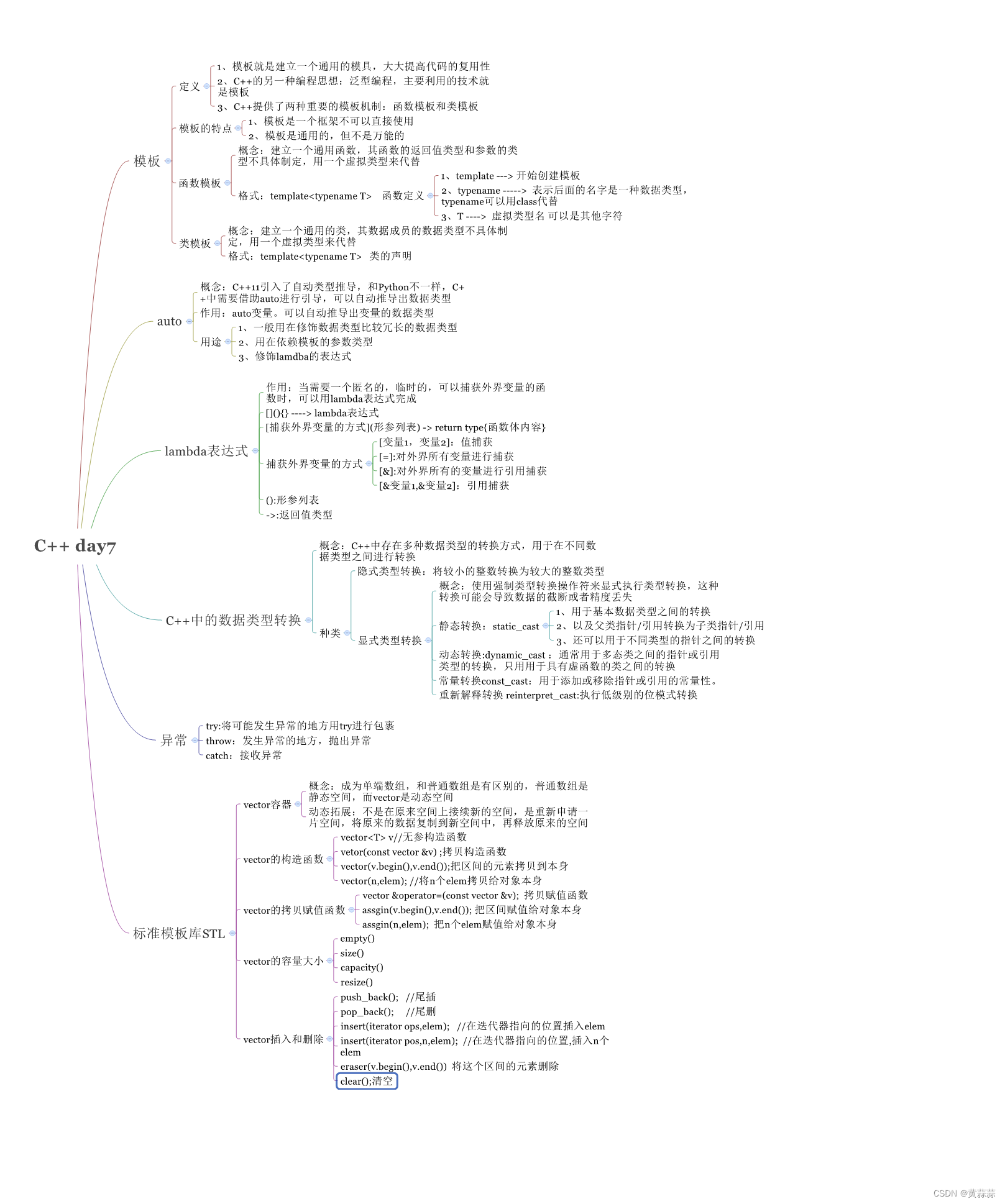
2024.3.19
思维导图...

【Python】新手入门学习:详细介绍单一职责原则(SRP)及其作用、代码示例
【Python】新手入门学习:详细介绍单一职责原则(SRP)及其作用、代码示例 🌈 个人主页:高斯小哥 🔥 高质量专栏:Matplotlib之旅:零基础精通数据可视化、Python基础【高质量合集】、PyT…...

【DataWhale学习笔记】使用AgentScope调用qwen大模型
AgentScope AgentScope介绍 AgentScope是一款全新的Multi-Agent框架,专为应用开发者打造,旨在提供高易用、高可靠的编程体验! 高易用:AgentScope支持纯Python编程,提供多种语法工具实现灵活的应用流程编排ÿ…...

【C++】手撕AVL树
> 作者简介:დ旧言~,目前大二,现在学习Java,c,c,Python等 > 座右铭:松树千年终是朽,槿花一日自为荣。 > 目标:能直接手撕AVL树。 > 毒鸡汤:放弃自…...
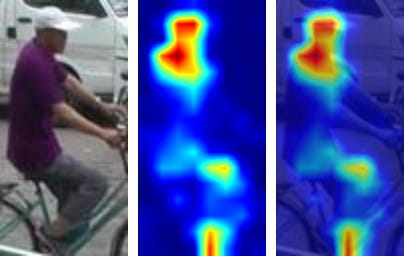
探索 TorchRe-ID--基于 Python 的人员再识别库
导言 人员再识别(re-ID)是计算机视觉中的一项重要任务,在监控系统、零售分析和人机交互中有着广泛的应用。TorchRe-ID 是一个功能强大、用户友好的 Python 库,它为人员再识别任务提供了一套全面的工具和模型。在本文中࿰…...

鸿蒙Harmony应用开发—ArkTS声明式开发(容器组件:Flex)
以弹性方式布局子组件的容器组件。 说明: 该组件从API Version 7开始支持。后续版本如有新增内容,则采用上角标单独标记该内容的起始版本。Flex组件在渲染时存在二次布局过程,因此在对性能有严格要求的场景下建议使用Column、Row代替。Flex组…...

tmux最基础的一点应用-不用一直挂着ssh,可以干点别的事情
文章目录 使用原因基础命令创建一个窗口退出当前窗口重新进入万一忘记了环境名字想要删除环境 使用原因 跑程序要很久,需要干别的事情,电脑不能一直开,可以使用tmux来管理。 基础命令 创建一个窗口 tmux new -s <你自己起的环境名字&g…...
Java推荐算法——特征加权推荐算法(以申请学校为例)
加权推荐算法 文章目录 加权推荐算法1.推荐算法的简单介绍2.加权推荐算法详细介绍3.代码实现4.总结 1.推荐算法的简单介绍 众所周知,推荐算法有很多种,例如: 1.加权推荐:分为简单的特征加权,以及复杂的混合加权。主要…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...
