企业是否具备等保测评资质在哪里查?怎么查?
为了规范等保相关业务办理流程,确保等保业务顺利办理,保障企业合法权益,政策规定,只有取得等保测评资质机构方可办理等保测评业务。因此很多人在问,企业是否具备等保测评资质在哪里查?怎么查?
企业是否具备等保测评资质在哪里查?怎么查?
【回答】:查询企业是否具备等保测评资质前往网络安全等级保护网查询即可。查询方式如下:
1、进入首页,找到最新动态,点击全国网络安全等级测评与检测评估机构目录进入查询即可;
2、进入首页,点击左侧信息查询里面的,全国网络安全等级测评与检测评估机构目录,输入机构名称进行查询即可。
内容补充1:等保测评机构申请条件
1、在中华人民共和国境内注册成立,由中国公民、法人投资或者国家投资的企事业单位;
2、产权关系明晰,注册资金 500 万元以上,独立经营核算,无违法违规记录;
3、从事网络安全服务两年以上,具备一定的网络安全检测评估能力;
4、法人、主要负责人、测评人员仅限中华人民共和国境内的中国公民,且无犯罪记录;
5、具有网络安全相关工作经历的技术和管理人员不少于 15 人,专职渗透测试人员不少于 2 人,岗位职责清晰, 且人员相对稳定;
6、具有固定的办公场所,配备满足测评业务需要的检测评估工具、实验环境等;
7、具有完备的安全保密管理、项目管理、质量管理、人员管理、档案管理和培训教育等规章制度;
8、不涉及网络安全产品开发、销售或信息系统安全集成等可能影响测评结果公正性的业务(自用除外);
9、应具备的其他条件。
内容补充2:选择等保测评机构四个注意事项
1、选择具有资质的机构。一定要查看等保测评机构是否具有正规资质,如果不清楚,可以登录网络安全等级保护网进行查询。
2、选择资质齐全的机构。除了等保测评资质后,还可以看看机构是否具有涉密资质、其他安全资质等证书。
3、考察测评机构实力。通过考察公司,看看公司实力怎么样,专业技术人员有多少,口碑怎么样等等。
4、查看机构案例。一般通过案例,我们可以知道该机构是否经验充足,这样过等保时候能够规避掉一些麻烦,更快速通过。
相关文章:

企业是否具备等保测评资质在哪里查?怎么查?
为了规范等保相关业务办理流程,确保等保业务顺利办理,保障企业合法权益,政策规定,只有取得等保测评资质机构方可办理等保测评业务。因此很多人在问,企业是否具备等保测评资质在哪里查?怎么查? …...

Spacedesk软件推荐,让你的平板也变成电脑的副屏
我的设备: 电脑:戴尔G15 5511、i7-11800H、Windows 11、RTX3060 平板:荣耀V6、麒麟985、安卓10、分辨率2000*1200(手机也行,我用的平板) 实际使用: 先给放一张实际使用的照片 可以让平板变成电脑的副屏…...

Vue 3.0 组合式API 介绍 【Vue3 从零开始】
提示 在阅读文档之前,你应该已经熟悉了这两个 Vue 基础和创建组件。 在 Vue Mastery 上观看关于组合式 API 的免费视频。 通过创建 Vue 组件,我们可以将接口的可重复部分及其功能提取到可重用的代码段中。仅此一项就可以使我们的应用程序在可维护性和…...

【算法数据结构体系篇class13、14】:贪心算法思想
一、贪心算法概念贪心算法概念:1)最自然智慧的算法2)用一种局部最功利的标准,总是做出在当前看来是最好的选择3)难点在于证明局部最功利的标准可以得到全局最优解4)对于贪心算法的学习主要以增加阅历和经验…...

C++知识点,关键字inline ,String,强制类型转化
🐶博主主页:ᰔᩚ. 一怀明月ꦿ ❤️🔥专栏系列:线性代数,C初学者入门训练 🔥座右铭:“不要等到什么都没有了,才下定决心去做” 🚀🚀🚀大家觉不错…...

MyBatis源码分析(六)MetaObject工具类的使用与源码分析
文章目录一、MetaObject基本使用二、关键类源码分析1、MetaObject的构造方法2、PropertyTokenizer分词器3、BeanWrapper4、MetaClass5、DefaultReflectorFactory6、Reflector7、总结三、MetaObject的getValue源码分析写在后面一、MetaObject基本使用 public class User {priva…...
文献资源最多的文献下载神器,99.99%的文献都可下载
用对工具事半功倍,查找下载文献用对工具能节约大量的时间和精力去做更多的事情。 文献党下载器(wxdown.org),几乎整合了所有文献数据库资源,涵盖各种文献类型,包含全部学科。文献党下载器整合的资源如&…...
工控机ARM工业边缘计算机搭建Node-Red环境
搭建Node-Red环境Node-RED是一个基于Node.js的开源可视化流程编程环境,可以轻松构建自定义应用程序,通过连接简单的节点来完成复杂的任务。Node-RED提供了一种简单的方法,可以快速连接到外部服务,从而实现物联网应用的开发。Node-…...

位图/布隆过滤器/海量数据处理方式
位图 位图的概念 所谓位图,就是用每一位来存放某种状态,适用于海量数据,数据无重复的场景。通常是用来判断某个数据存不存在的。 直接来看问题: 给40亿个不重复的无符号整数,没排过序。给一个无符号整数࿰…...
Tomcat 配置文件数据库密码加密
几年前研究过Tomcat context.xml 中数据库密码改为密文的内容,因为当时在客户云桌面代码没有留备份也没有文章记录,最近项目又提出了这个需求就又重新拾起来学习一下。在网上找了一些资料,自己也大概试了一下,目前功能是实现了。参…...
k8s-Kubernetes集群部署
文章目录前言一、Kubernetes简介与架构1.Kubernetes简介2.kubernetes设计架构二、Kubernetes集群部署1.集群环境初始化2.所有节点安装kubeadm3.拉取集群所需镜像3.集群初始化4.安装flannel网络插件5.扩容节点6.设置kubectl命令补齐前言 一、Kubernetes简介与架构 1.Kubernetes…...

Python数据分析案例19——上市银行财务指标对比
我代码栏目都是针对基础的python数据分析人群,比如想写个本科毕业论文,课程论文,做个简单的案例分析等。过去写的案例可能使用了过多的机器学习和深度学习方法,文科的同学看不懂,可能他们仅仅只想用python做个回归或者…...

Python 中错误 ConnectionError: Max retries exceeded with url
出现错误“ConnectionError: Max retries exceeded with url”有多种原因: 向 request.get() 方法传递了不正确或不完整的 URL。我们正受到 API 的速率限制。requests 无法验证您向其发出请求的网站的 SSL 证书。 确保我们指定了正确且完整的 URL 和路径。 # ⛔️…...

SpringBoot下的Spring框架学习(Tedu)——DAY02
SpringBoot下的Spring框架学习(Tedu)——DAY02 目录SpringBoot下的Spring框架学习(Tedu)——DAY02Spring框架学习1.1 Spring介绍1.2 知识铺垫1.2.1 编辑Dog类1.2.2 编辑Cat类1.2.3 编辑测试类User.java1.2.4 上述代码的总结1.3 面…...

容易混淆的点:C语言中char* a[] 与 char a[] 的区别以及各自的用法
char* a[] 和 char a[] 的区别 char* a[] 和 char a[] 是 C 语言中数组的不同声明方式,二者具有以下区别: char a[] 声明的是一个字符数组,其中存储的是一串字符。此时,a 可以被视为一个指向字符的指针。 char* a[]则声明了一个…...
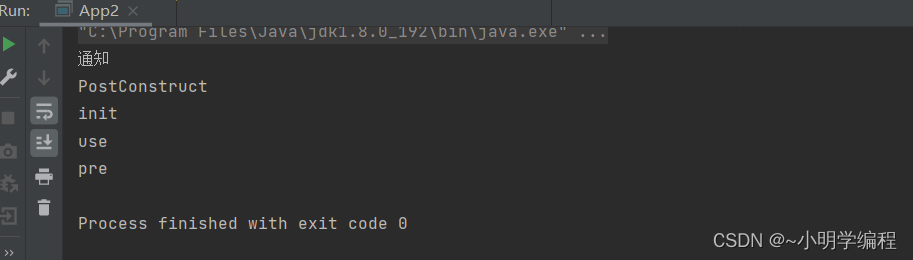
认识Spring(下)
作者:~小明学编程 文章专栏:Spring框架 格言:热爱编程的,终将被编程所厚爱。 目录 Spring更加高效的读取和存储对象 存储bean对象 五大注解 关于五大类注解 对象的注入 属性注入 构造方法注入 Setter注入 三种注入方式的…...
 C - Maximum Set)
Educational Codeforces Round 144 (Rated for Div. 2) C - Maximum Set
传送门 题意: 对于一个集合,如果它的任意两个元素都能 有 其中一个能整除另一个,那么它是好的。问在区间[L,R] 中由这个区间某些数内构成的好的集合的最长长度是多少,以及且满足这个长度的好集合有多少个。(懒得想就借…...
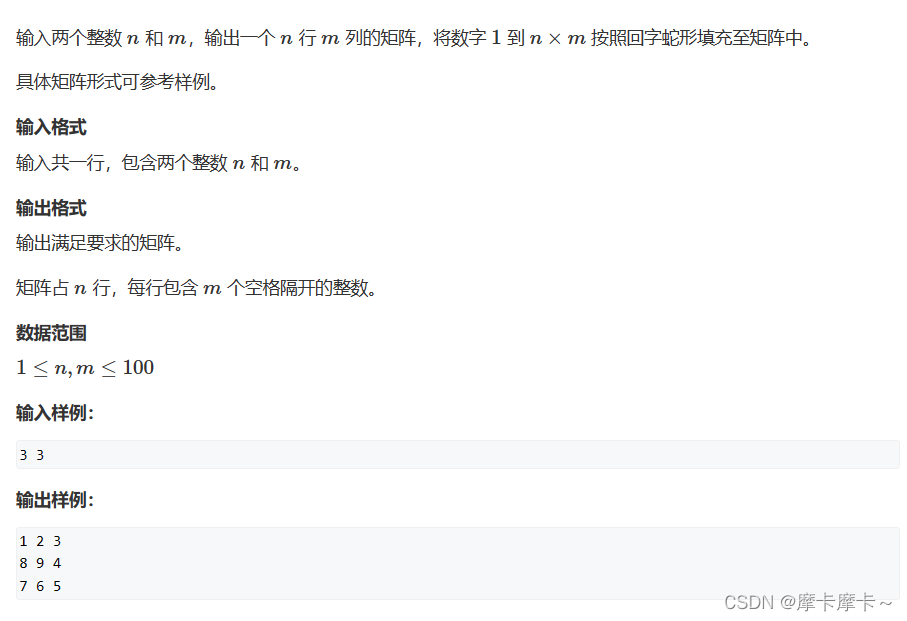
学python的第四天---基础(2)
一、三角形类型读入数组并排序的方法nlist(map(float,input().split())) c,b,asorted(n)list_1 list(map(float, input().split())) list_1.sort() list_1.reverse()lengthssorted(map(float,input().split(" ")),reverseTrue)二、动物写法一:d{" &…...
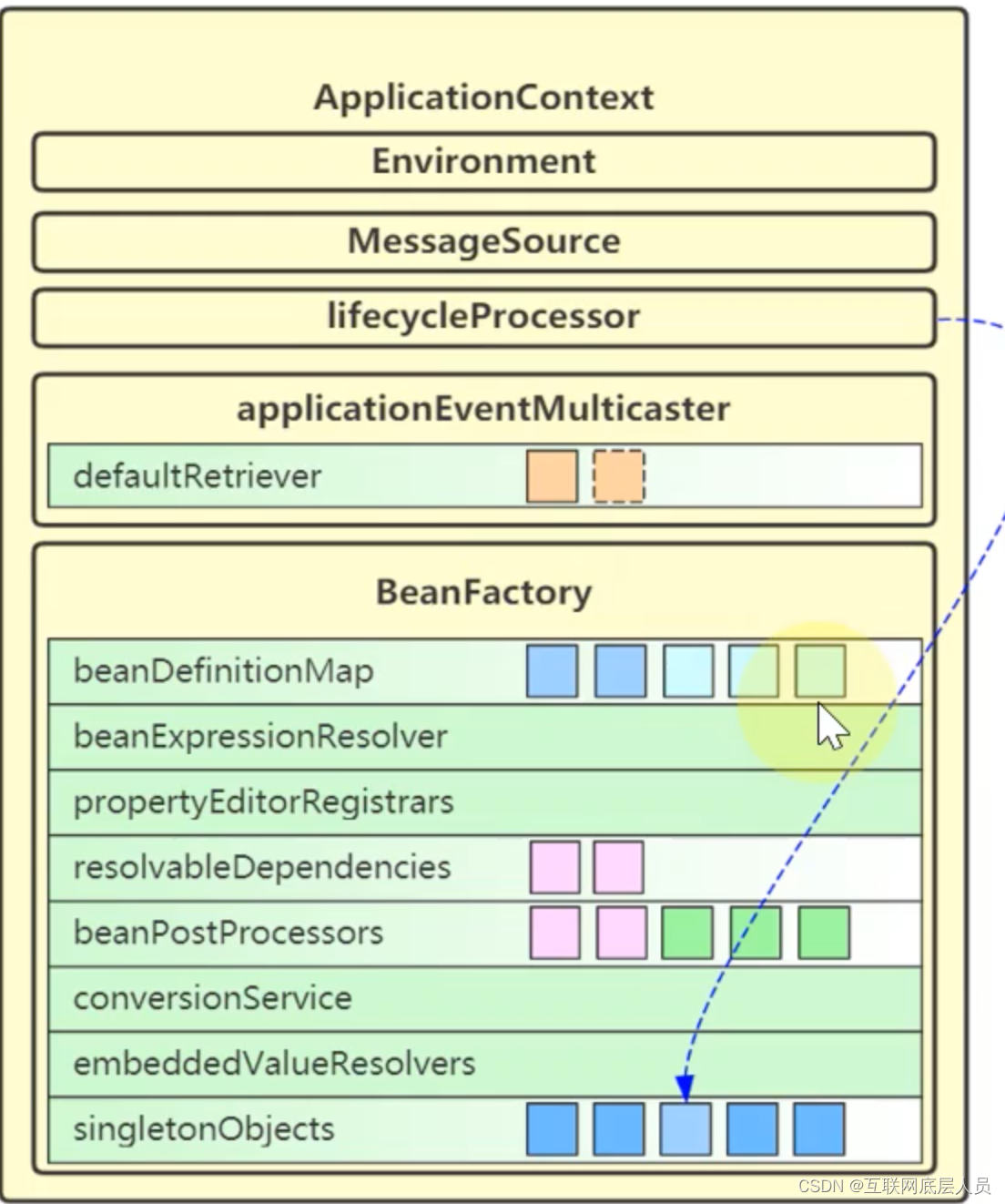
spring之refresh流程-Java八股面试(六)
系列文章目录 第一章 ArrayList-Java八股面试(一) 第二章 HashMap-Java八股面试(二) 第三章 单例模式-Java八股面试(三) 第四章 线程池和Volatile关键字-Java八股面试(四) 第五章ConcurrentHashMap-Java八股面试(五) 动态每日更新算法题,想要学习的可以关注一下…...
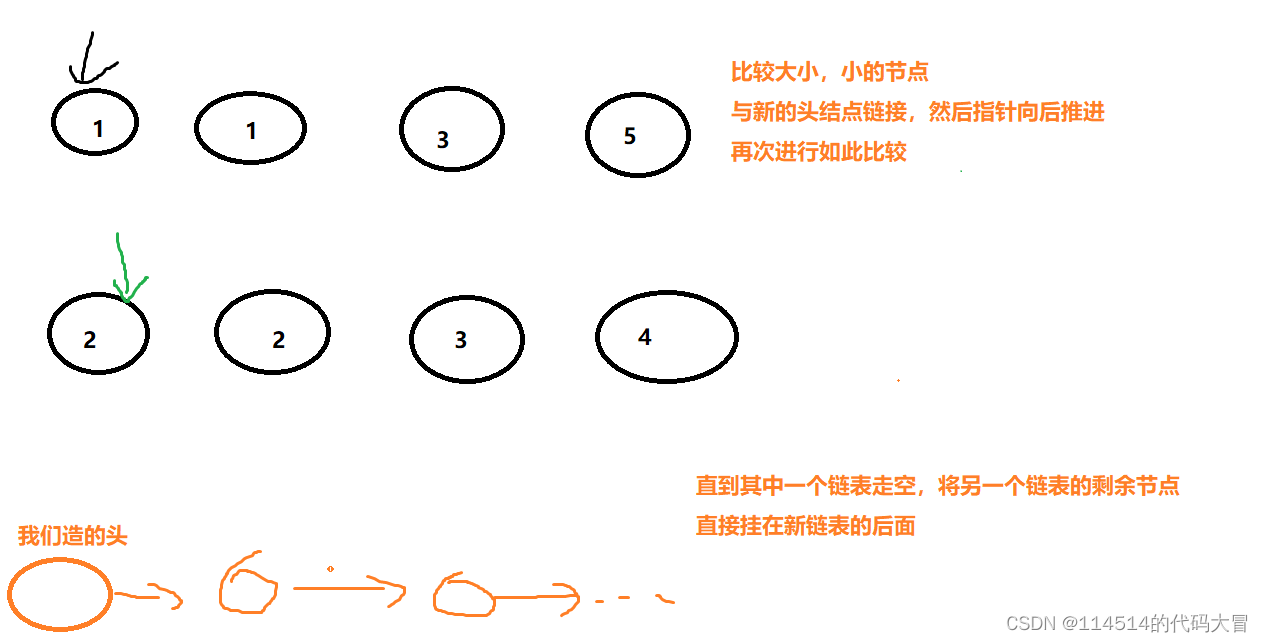
【C语言】刷题|链表|双指针|指针|多指针|数据结构
主页:114514的代码大冒 qq:2188956112(欢迎小伙伴呀hi✿(。◕ᴗ◕。)✿ ) Gitee:庄嘉豪 (zhuang-jiahaoxxx) - Gitee.com 文章目录 目录 文章目录 前言 一、移除链表元素 二、反转链表 三,链表的中间结点 四&…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...
