显著性检验【t-test、方差分析、ks检验】
显著性检验【t-test、方差分析、ks检验】
0、目录
1显著性检验基本定义(what?)
2.使用显著性检验的意义(why? )
3.显著性检验的具体操作流程(how? )
1、显著性检验基本定义
- 统计假设检验(Statistical hypothesis testing)
- 事先对总体(随机变量)的 参数或总体分布形式做出一个假设,然后利用样本信息来判断这个假设是否合理
- 显著性检验(significance test)
- 统计假设检验的一种
- 显著性检验是用于检测科学实验中实验组与对照组之间是否有差异以及差异是否显著的办法。
- 在使用显著性检验之前必须先进行统计假设,也就是无效假设/零假设/原假设
- 无效假设/零假设/原假设(null hypothesis)
- 数据结果之间本身不存在显著性差异
- 指进行统计检验时预先建立的假设。 零假设成立时,有关统计量应服从已知的某种概率分布。
- 当统计量的计算值落入否定域时,可知发生了小概率事件,应否定原假设。
若原假设为真,而检验的结论却劝你放弃原假设。此时,我们把这种错误称之为第一类错误。通常把第一类错误出现的概率记为α若原假设不真,而检验的结论却劝你采纳原假设。此时,我们把这种错误称之为第二类错误。通常把第二类错误出现的概率记为β- 通常只限定犯第一类错误的最大概率α, 不考虑犯第二类错误的概率β。我们把这样的假设检验称为显著性检验,概率α称为显著性水平。
2.使用显著性检验的意义
- 实例讲解
- 一个球迷想要评价c罗和梅西的网络影响力,下列分别为二人在2017年每月社交网络发布后获得的点赞量/评论量,想要知道二人是否有存在明显的差异
- CR7= {23,25,26,27,23,24,22,23,25,29,30,32}
- Messi= {24,25,23,26,27,25,25,28,30,31,29,28}
- 根据零假设的定义,作出“两人的点赞量没有显著差异”的假设,最后计算得出,方差检验的p_value= 0.459,那也就意味着两人的点赞量并没有明显的差异
3、显著性检验的具体操作流程
方差分析
- 方差分析(Analysis of Variance,简称ANOVA),又称“变异数分析”,是R.A.Fisher发明的,用于两个及两个以上样本均数差别的显著性检验
- 在显著性水平α =0.05的情况下,p>0.05接受原假设,p值<0.05拒绝原假设
- 原假设是二人间不存在显著性差异,由于p=0.459>0.05,所以接受原假设,即二人间不存在显著性差异
- 如果这里的p值小于0.05,那么就要拒绝原假设,即二人间存在显著性差异
- p_value的另一种理解
- 实例中的p_value=0.459,意思就是说偶然因素导致数据发生这种差异的概率是0.459,跟0.05一比大好多。那么就是说偶然因素很有可能导致了这种差异,所以数据本身之间是不存在差异的。
'''方差齐性检验 在显著性水平α =0.05的情况下,p>0.05接受原假设, 所以接受原假设,即样本集B和样本集H间不存在显著性差异'''from scipy import stats # 导入相应模块v3=[23,25,26,27,23,24,22,23,25,29,30,32] v4=[24,25,23,26,27,25,25,28,30,31,29,28]stats.levene(v3,v4, center="mean") fVal, pSD = stats.levene(v3,v4, center="mean")print("ANOVA-0",fVal, pSD)输出结果:
0.5671069450362157
0.45939425229350794
T 检验(T-Test)
- T 检验用于确定两个变量的均值之间是否存在显著差异,并判断它们是否属于同一分布
- 双尾测试
- 函数 ttest_ind() 获取两个相同大小的样本,并生成 t 统计和 p 值的元组
- 查找给定值 v1 和 v2 是否来自相同的分布:
'''T-test 在显著性水平α =0.05的情况下,p>0.05接受原假设, 所以接受原假设,即样本集B和样本集H间不存在显著性差异'''v3=[23,25,26,27,23,24,22,23,25,29,30,32] v4=[24,25,23,26,27,25,25,28,30,31,29,28]import numpy as np from scipy.stats import ttest_ind from scipy import statsres = ttest_ind(v3, v4) print(res)输出结果
Ttest_indResult(statistic=-0.8599394154935148, pvalue=0.3990967787539713)
KS 检验
-
KS 检验用于检查给定值是否符合分布
-
该函数接收两个参数;测试的值和 CDF
- CDF 为累积分布函数(Cumulative Distribution Function),又叫分布函数。CDF 可以是字符串,也可以是返回概率的可调用函数。
-
可以用作单尾或双尾测试,默认情况下它是双尾测试。 我们可以将参数替代作为两侧、小于或大于其中之一的字符串传递。
-
查找给定值是否符合正态分布
import numpy as np from scipy.stats import kstestv = np.random.normal(size=100)res = kstest(v, 'norm')print(res)输出结果
KstestResult
(statistic=0.047798701221956841, pvalue=0.97630967161777515)
相关文章:

显著性检验【t-test、方差分析、ks检验】
显著性检验【t-test、方差分析、ks检验】 0、目录 1显著性检验基本定义(what?) 2.使用显著性检验的意义(why? ) 3.显著性检验的具体操作流程(how? ) 1、显著性检验基本定义 统计假设检验…...

访问学者在德国访学生活衣食住行攻略
德国因其优质的教育水平、高价值的学制、低廉的访学成本,逐渐成为访学领域的宠儿。对于初次来到德国生活的访问学者,一定不是很熟悉德国的真实生活情况。今天51访学网小编就给大家介绍德国访学学衣食住行,希望可以帮助到即将出国的你。 一、…...

SQL-刷题技巧-删除重复记录
一. 原题呈现 牛客 SQL236. 删除emp_no重复的记录,只保留最小的id对应的记录。 描述: 删除emp_no重复的记录,只保留最小的id对应的记录。 drop table if exists titles_test; CREATE TABLE titles_test (id int(11) not null primary key…...

基于JSP的虚拟账号交易平台
技术:Java、JSP等摘要:随着网络游戏以及各种平台的出现与更新,虚拟账号交易平台正逐渐成为电商的新增长点。当今社会,互联网发发展飞速,游戏产业也渐渐兴起,随之虚拟游戏账号的交易量逐渐增多,但…...

LeetCode201_201. 数字范围按位与
LeetCode201_201. 数字范围按位与 一、描述 给你两个整数 left 和 right ,表示区间 [left, right] ,返回此区间内所有数字 按位与 的结果(包含 left 、right 端点)。 示例 1: 输入:left 5, right 7 输…...

一款好的风险管理软件可以做什么
风险管理软件哪个好?使用Zoho Projects易于使用的项目风险管理软件,最大限度地减少收入损失并快速调整您的投资组合,保护您的项目投资。Zoho Projects的高级风险管理软件可在您最需要的时候安全的保护您的业务。使用Zoho Projects强大的风险管…...

html2canvas使用文档
一、安装 Install NPM npm install --save html2canvasInstall Yarn yarn add html2canvas二、引入 import html2canvas from html2canvas;三、使用 以 vue 举例,这样写起来比较方便 <div ref"picture"><h4>Hello world!</h4> &l…...

HTML DOM 改变 CSS
HTML DOM 允许 JavaScript 改变 HTML 元素的样式。改变 HTML 样式如需改变 HTML 元素的样式,请使用这个语法:document.getElementById(id).style.propertynew style 下面的例子会改变 <p> 元素的样式:实例<html><body><…...
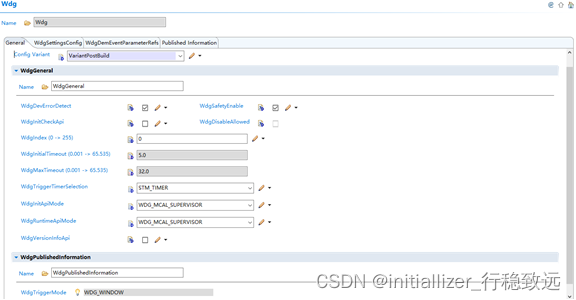
基于EB工具的TC3xx_MCAL配置开发01_WDG模块配置介绍
目录 1.概述2. WDG 配置2.1 General部分配置2.2 WdgSettingsConfig配置2.2.1 配置概述2.2.2 CPU WDG具体配置2.3 WdgDemEventParameterRefs3. WDG配置注意事项1.概述 本篇开始我们基于EB Tresos工具对英飞凌TC3xx系列MCU的MCAL开发进行介绍,结合项目经验对各MCAL外设的开发及…...

Activty启动到显示的过程[二]
Activity的显示从handleResumeActivity()方法开始。 //ActivityThread.javaOverridepublic void handleResumeActivity(IBinder token, boolean finalStateRequest, boolean isForward,String reason) {final ActivityClientRecord r performResumeActivity(token, finalStat…...
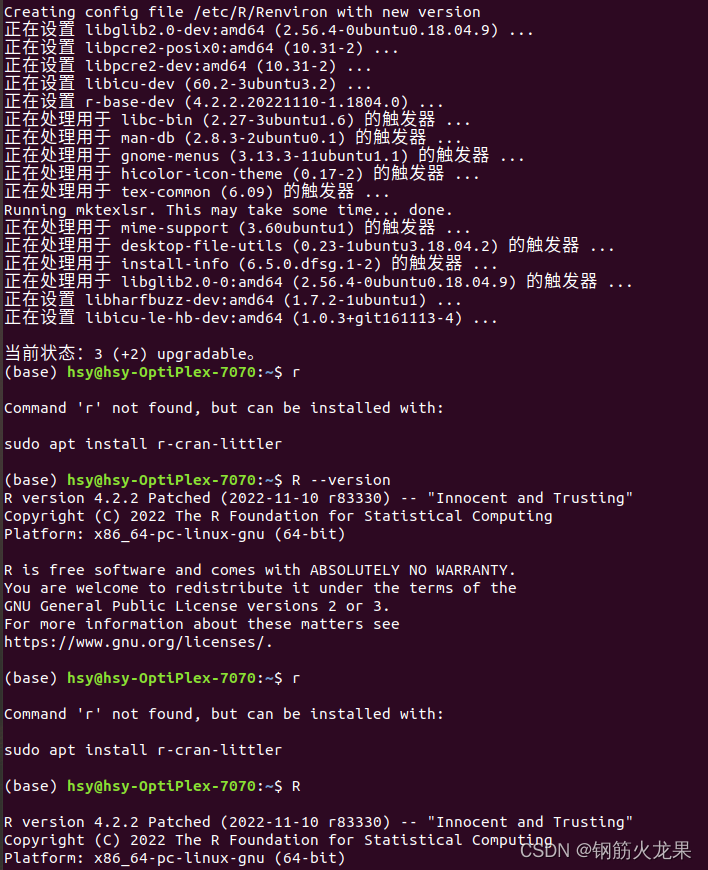
ubuntu 18.04.06LST安装R4.0+版本报错及解决过程
1. sudo apt-get update无法正常使用 错误:13 http://ppa.launchpad.net/webupd8team/sublime-text-3/ubuntu bionic Release 404 Not Found [IP: 2620:2d:4000:1::3e 80] 解决措施:删除 webupd8team/sublime-text-3这个ppa文件。 sudo add-apt-repository --…...

数据湖架构Hudi(五)Hudi集成Flink案例详解
五、Hudi集成Flink案例详解 5.1 hudi集成flink flink的下载地址: https://archive.apache.org/dist/flink/ HudiSupported Flink version0.12.x1.15.x、1.14.x、1.13.x0.11.x1.14.x、1.13.x0.10.x1.13.x0.9.01.12.2 将上述编译好的安装包拷贝到flink下的jars目录…...

【Java学习笔记】9.Java 循环结构 - for, while 及 do...while
Java 循环结构 - for, while 及 do…while 顺序结构的程序语句只能被执行一次。 如果您想要同样的操作执行多次,就需要使用循环结构。 Java中有三种主要的循环结构: while 循环do…while 循环for 循环 在 Java5 中引入了一种主要用于数组的增强型 f…...

【面向对象初步】之面向对象VS面向过程
面向对象(ObjectorientedProgramming,OOP)编程的思想主要是针对大型软件设计而来的。面向对象编程使程序的扩展性更强、可读性更好,使的编程可以像搭积木一样简单。 面向对象编程将数据和操作数据相关的方法封装到对象中,组织代码和数据的方式更加接近人的思维,从而大大提…...

原型链(回顾)
概念prototype__proto__原型链查找机制万物皆对象判断私有/共有属性方法Object.prototype.prototype nullObject.create(proto, [propertiesObject])给类的原型上扩展属性方法的4种方法Fn.prototype.xxx xxxObject.prototype.xxx xxxf1.proto.xxx xxx原型重定向 概念 原型…...

DS内排—2-路归并排序
目录 题目描述 AC代码 题目描述 输入一组字符串,用2-路归并排序按字典顺序进行降序排序。 输入 测试次数t 每组测试数据:数据个数n,后跟n个字符串,字符串不含空格。 输出 对每组测试数据,输出2-路归并排序的每…...
第 3 部分:Wallet创建)
深度账户抽象(Account Abstraction)第 3 部分:Wallet创建
Wallet创建 我们还没有解决的是每个用户的钱包合约最初是如何在区块链上结束的。部署合约的“传统”方式是使用 EOA 发送包含合约部署代码的且没有收件人的交易。这在这里会非常令人不满意,因为我们刚刚做了很多工作来实现它,所以有人可以在没有 EOA 的情况下与链交互。如果用…...

代码分享:面波数据快速成图
代码分享:面波数据快速成图 前言 目前,物探数据主要用surfer软件成图,surfer软件具有强大的插值和绘图功能,成图比较美观。但是,生产过程中大量的物探数据,依靠excel和surfer来成图耗费人力时间成本。本博…...

常见数据结构
一. 数据结构概述、栈、队列 1. 数据结构概述 2. 栈数据结构的执行特点 3. 常见数据结构之队列 二. 常见数据结构之数组 数组它就是内存中的一块儿连续区域。数组变量存的是数组在堆内存当中的起始地址。数组查询任意索引位置的值耗时相同,数组根据索引查询速度快。…...
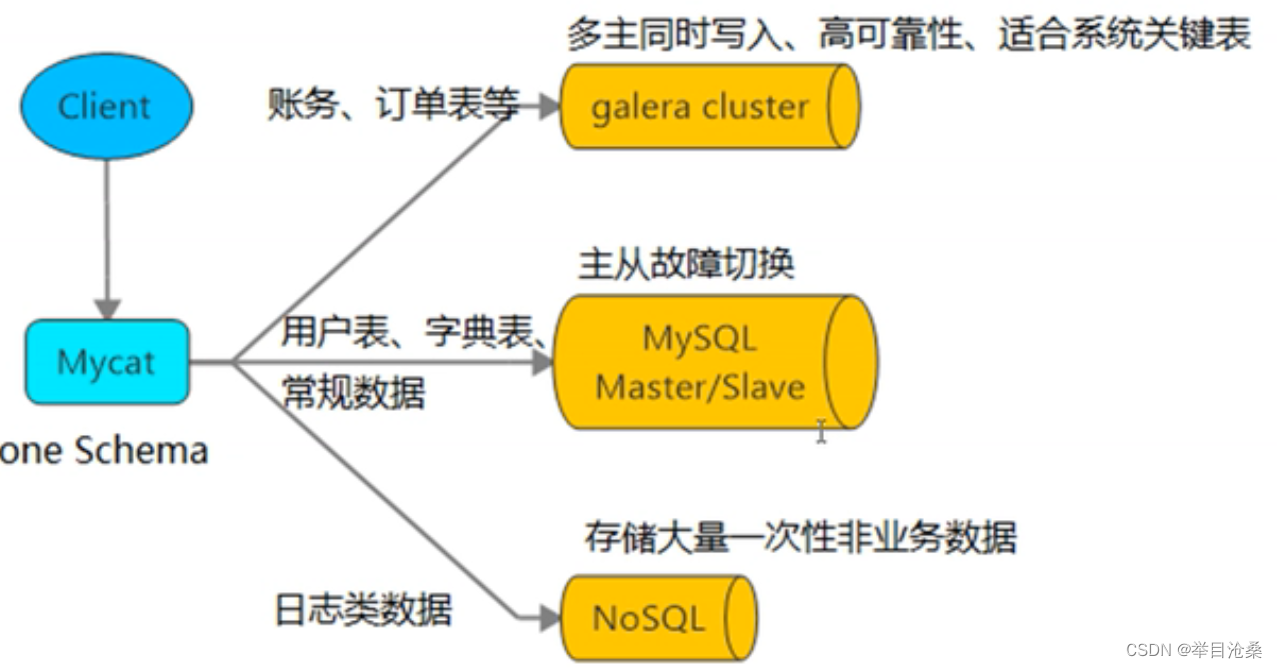
Mycat
Mycat 1.概述 1.Mycat是数据中间件2.中间件:连接软件组件和应用的计算机软件,便于软件和各部件的交互3.数据中间件:连接Java应用程序与数据库的软件2.适用场景 1.Java与数据库紧耦合(直接连接)2.高访问量高并发对数据库压力(集群)3.读写请求数据不一致(读写分离+主从复制)3.…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...
