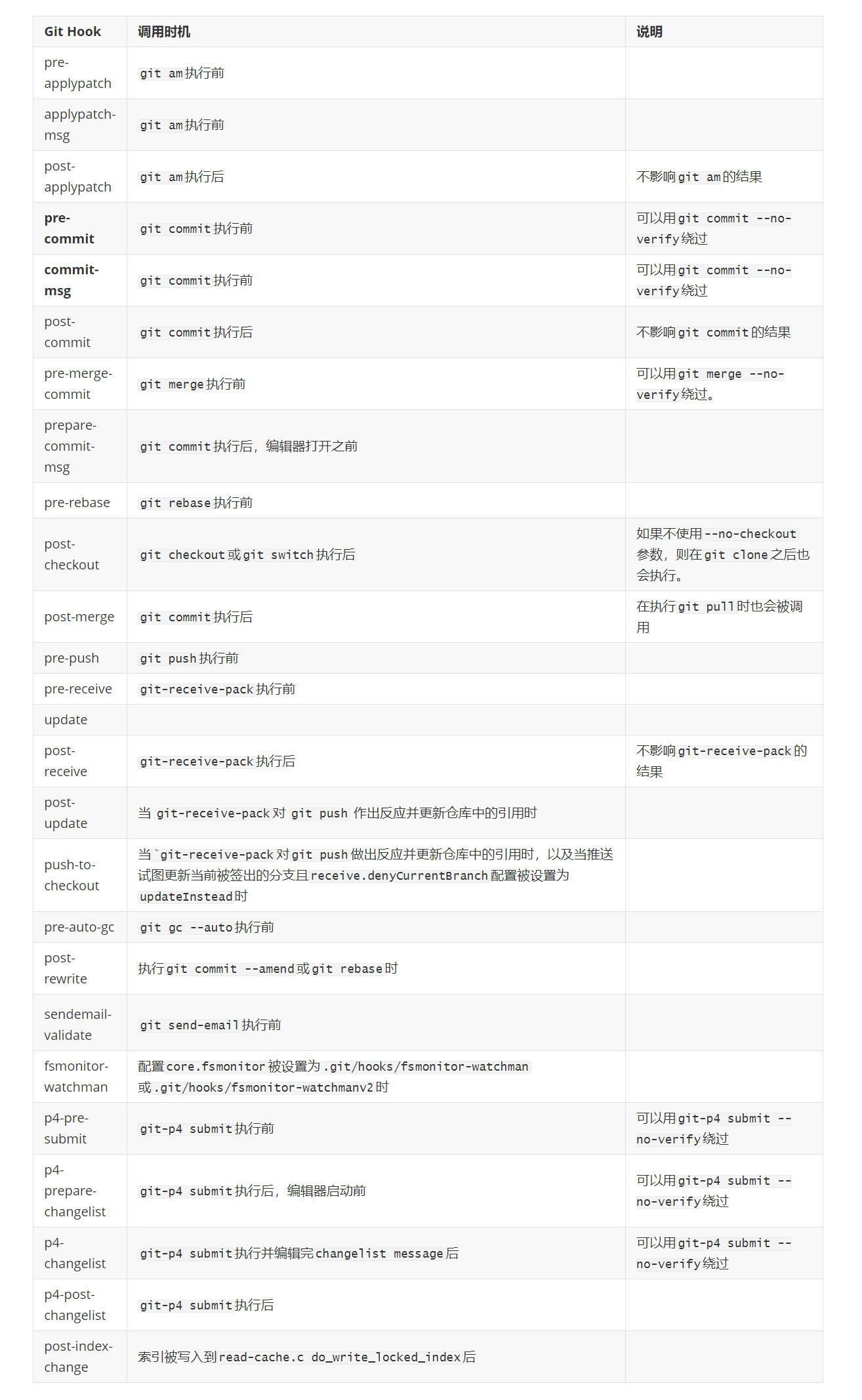
Leetcode DAY 56: 两个字符串的删除操作 and 编辑距离
- 583. 两个字符串的删除操作
1 、 dp[i][j] 表示 让以word1[i - 1]为结尾的字符串 和 以word2[i - 2]为结尾的字符串 相等需要删除的最少次数
1、dp[i][j] 的 递推需要考虑两种情况:
(1)word1[i - 1] == word2[j - 1] 相当于不考虑word1[i]和word2[j] 只考虑前面的 所以dp[i][j] = dp[i - 1][j - 1]
(2)word1[i - 1] != word2[j - 1] ;如果不考虑word1[i - 1] 那么dp[i][j] = dp[i - 1][j] + 1; 如果不考虑word2[j - 1] 那么dp[i][j] = dp[i][j - 1] + 1 ; 如果都不考虑 那么dp[i][j] = dp[i - 1][j - 1] + 2
class Solution {
public:int minDistance(string word1, string word2) {int n = word1.size();int m = word2.size();vector<vector<int>> dp(n + 1, vector<int>(m + 1));//dp[0][j] for(int i = 0; i <= n; i++) dp[i][0] = i;for(int j = 0; j <= m; j++) dp[0][j] = j;for(int i = 1; i <= n; i++) {for(int j = 1; j <= m; j++) {if(word1[i - 1] == word2[j - 1]) {dp[i][j] = dp[i - 1][j - 1];} else {dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);}}}return dp[n][m];}
};- 72. 编辑距离
1、dp[i][j]表示 以word1[i - 1]为结尾的字符串 -> 以word2[j - 1]为结尾的字符串需要的最少操作次数
2、 word1[i - 1] & word2[j - 1]相等 ->不操作 dp = dp[i -1][j - 1]
不相等 可以进行 (增 删 换)
(1)增: 相当于 不考虑word2[j - 1] 操作数 + 1
(2) 删 :相当于 不考虑word2[i -1] 操作数 + 1
(3) 换:相当于 把word1[i - 1] 替换成word2[j - 1] 相当于 不考虑这俩 操作数 + 1
class Solution {
public:int minDistance(string word1, string word2) {int n = word1.size();int m = word2.size();vector<vector<int>> dp(n + 1, vector<int>(m + 1));// dp[i][0]for(int i = 0; i <= n; i++) dp[i][0] = i;for(int j = 0; j <= m; j++) dp[0][j] = j; for(int i = 1; i <= n; i++) {for(int j = 1; j <= m; j++) {if(word1[i - 1] == word2[j - 1]) {dp[i][j] = dp[i - 1][j - 1];} else {dp[i][j] = min(dp[i - 1][j] + 1, min(dp[i][j - 1] + 1, dp[i - 1][j - 1] + 1));}}}return dp[n][m];}
};相关文章:

Leetcode DAY 56: 两个字符串的删除操作 and 编辑距离
583. 两个字符串的删除操作 1 、 dp[i][j] 表示 让以word1[i - 1]为结尾的字符串 和 以word2[i - 2]为结尾的字符串 相等需要删除的最少次数 1、dp[i][j] 的 递推需要考虑两种情况: (1)word1[i - 1] word2[j - 1] 相当于不考虑word1[i]和…...

系统检测维护工具Wsycheck使用(18)
实验目的 (1)学习Wsycheck的基本功能; (2)掌握Wsycheck的基本使用方法; 预备知识 windows操作系统的基本知识如:进程、网络、服务和文件等的了解。 Wsycheck是一款强大的系统检测维护工具,进程和…...

111 ok
全部 答对 答错 单选题 1.在与团队一起召开开工会议之后,项目经理分配工作活动,由于与其职能经理分配的任务发生冲突,一位团队成员拒绝开始工作,项目经理首先应该做什么? A请项目发起人帮助与职能经理进行谈判 B签发…...

Python API教程:API入门
什么是API? 一个API,或被称为应用程序接口,是一个服务器为你提供一个接收或发送数据的代码。API通常用来接收数据。 本文就集中焦点在此话题中。 当我们想从一个API中接收数据,我们需要开始请求。请求可以包含整个Web。例如&am…...
SpringMVC学习笔记
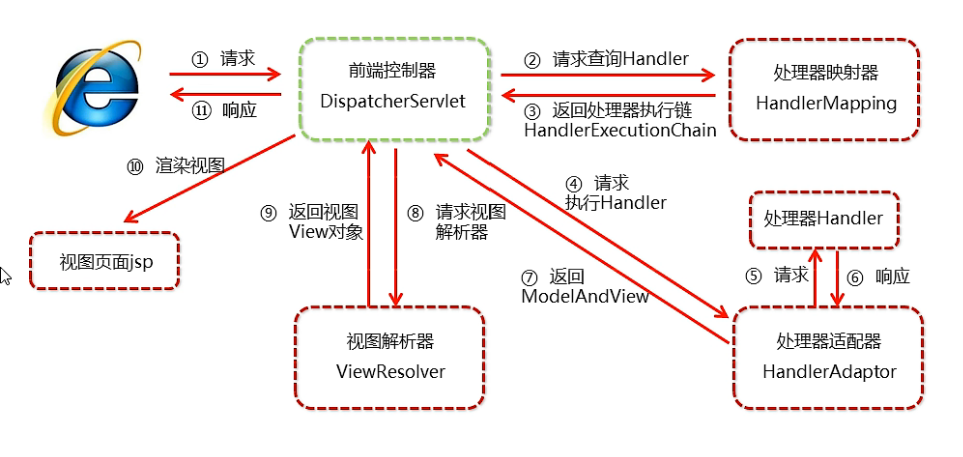
文章目录一、SpringMVC简介1、MVC与三层架构1.1 M1.2 V1.3 C1.4 MVC模式的工作流程1.5 三层架构2、什么是SpringMVC3、SpringMVC的特点二、搭建项目框架1、web项目结构2、创建maven工程,配置pom.xmla>添加web模块b> pom.xml中设置打包方式:warc>…...

Linux学习记录01
文章目录1. Linux基础知识2. Linux常用命令2.1 基础知识2.2 ls命令2.3 cd pwd命令2.4 mkdir2.5 touch、cat、more2.6 cp、mv、rm2.7 通配符、root模式2.8 whicih、find命令2.9 grep、mc、| 管道符2.10 echo、反引号、tail、重定向符2.11 vi、vm文本编辑器1. Linux基础知识 Lin…...
VScode 插件【配置】
写这篇博客的原因: vscode 很久以前的插件,忘记是干什么的了记录 vscode 好用的插件 插件介绍(正文开始) Auto Rename tag 开始/关闭标签内容 同步 Chinese (Simplified) VScode 中文化 CSS Peek 通过 html 代码查找到引用的样式…...
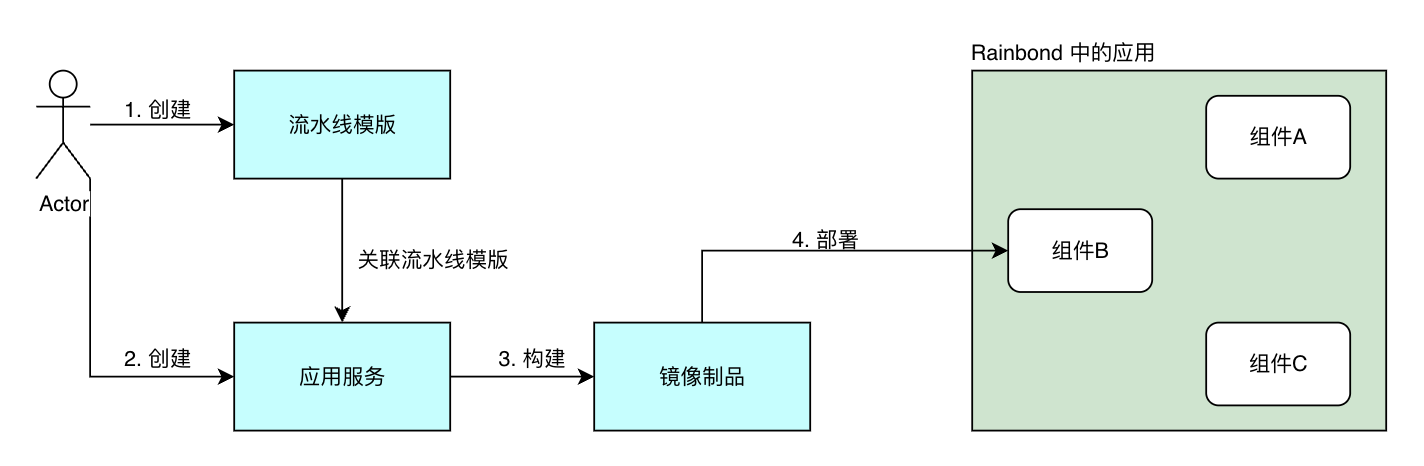
基于 Rainbond 的 Pipeline(流水线)插件
背景 Rainbond 本身具有基于源码构建组件的能力,可以将多种编程语言的代码编译成 Docker 镜像,但是在持续集成的过程中,往往会需要对提交的代码进行静态检查、构建打包以及单元测试。之前由于 Rainbond 并没有 Pipeline 这种可编排的机制&am…...

ASGARD:单细胞导向的药物发现
异质性,或更具体地说,病变组织中的不同的细胞群,是许多复杂疾病治疗失败的主要原因(如癌症、阿尔茨海默症、中风和COVID-19等),也是精准医疗成功的主要障碍。近年来,单细胞技术,特别…...

js-DOM03-事件
事件(Event) - 事件对象 - 当响应函数被调用时,浏览器每次都会将一个事件对象作为实参传递进响应函数中, 这个事件对象中封装了当前事件的相关信息,比如:鼠标的坐标,键盘的按键…...

天梯赛题目练习L1-007--L1-009
1、L1-007 念数字 题目详情 - L1-007 念数字 (pintia.cn) 分数 10 输入一个整数,输出每个数字对应的拼音。当整数为负数时,先输出fu字。十个数字对应的拼音如下: 0: ling 1: yi 2: er 3: san 4: si 5: wu 6: liu 7: qi 8: ba 9: jiu输入格…...

来吧!接受Kotlin 协程--线程池的7个灵魂拷问
前言 之前有分析过协程里的线程池的原理:Kotlin 协程之线程池探索之旅(与Java线程池PK),当时偏重于整体原理,对于细节之处并没有过多的着墨,后来在实际的使用过程中遇到了些问题,也引发了一些思考,故记录之…...

Dynamic Movement Primitives (DMP) 学习
Dynamic Movement Primitives (DMP) 学习 【知乎】Dynamic Movement Primitives介绍及Python实现与UR5机械臂仿真 1. DMP的建模过程 链接:Dynamic Movement Primitives介绍及Python实现与UR5机械臂仿真 - 知乎 (zhihu.com) 沙漏大佬!!&am…...
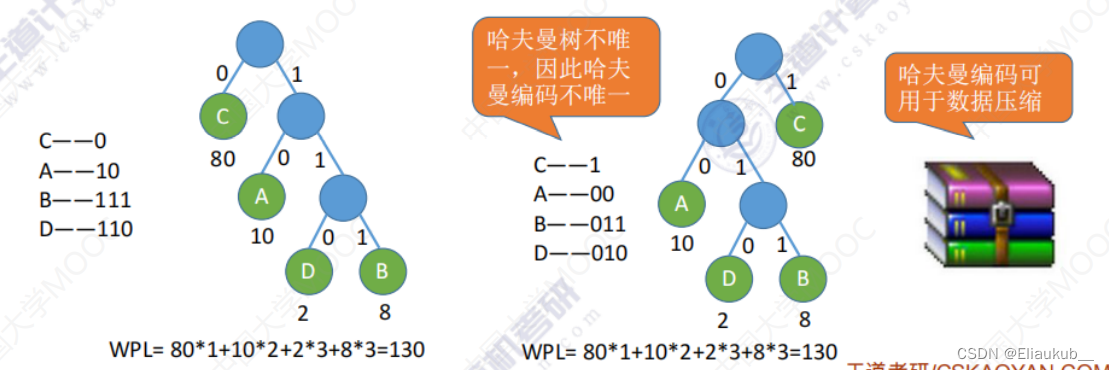
2023王道考研数据结构笔记第五章——树
第五章 树 5.1 树的基本概念 树是n(n≥0)个结点的有限集合,n 0时,称为空树。 空树——结点数为0的树 非空树——①有且仅有一个根节点 ②没有后继的结点称为“叶子结点”(或终端结点) ③有后继的结…...

setState函数是异步的还是同步的?
setState函数是异步的还是同步的? 可能很多同学在看到这个问题的时候,甚至搞不清楚这个问题在问什么。 不要慌,我们看一下下面这个例子,首先我们创建一个类组件,这个类组件中,我们定义了state是一个对象,对象中有一个…...
vue3+ts:约定式提交(git husky + gitHooks)
一、背景 Git - githooks Documentation https://github.com/typicode/husky#readme gitHooks: commit-msg_snowli的博客-CSDN博客 之前实践过这个配置,本文在vue3 ts 的项目中,再记录一次。 二、使用 2.1、安装 2.1.1、安装husky pnpm add hus…...
TSP 问题求解的最好方法 LKH
目前可以查到的最好的方法求解TSP问题是 LKH,所以本篇文章介绍如何使用Matlab 调用LKH 参考文档:用matlab调用迄今为止最强悍的求解旅行商(TSP)的算法-LKH算法_wx6333e948c3602的技术博客_51CTO博客 【LKH算法体验】用matlab调用…...
RocketMQ5.1控制台的安装与启动
RocketMQ控制台的安装与启动下载修改配置开放端口号重启防火墙添加依赖编译 rocketmq-dashboard运行 rocketmq-dashboard本地访问rocketmq无法发送消息失败问题。connect to <公网ip:10911> failed下载 下载地址 修改配置 修改其src/main/resources中…...
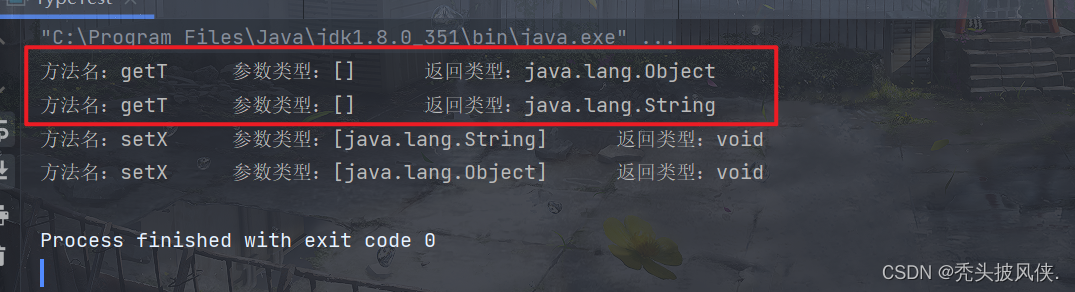
【java基础】类型擦除、桥方法、泛型代码和虚拟机
文章目录基础说明类型擦除无限定有限定转换泛型表达式方法类型擦除(桥方法)关于重载的一些说明总结基础说明 虚拟机没有泛型类型对象一所有对象都属于普通类。在泛型实现的早期版本中,甚至能够将使用泛型的程序编译为在1.0虚拟机上运行的类文…...

十家公司有九家问过的软件测试面试题,最后一题我猜你肯定不会
最近面试了一些测试方面相关的岗位,通过牛客等途径也看了不少的面经,发现大部分人面试题目都有很多相似点,结合自己的一些面试经历,现在分享一些我面试中碰到过的问题 常见的面试题 1、jmeter的加密参数如何入参? 2…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...
