哈希表题目:数组中的 k-diff 数对
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 解法
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:数组中的 k-diff 数对
出处:532. 数组中的 k-diff 数对
难度
4 级
题目描述
要求
给定一个整数数组 nums\texttt{nums}nums 和一个整数 k\texttt{k}k,返回不同的 k\texttt{k}k-diff 数对的数目。
一个 k\texttt{k}k-diff 数对为一个整数对 (nums[i],nums[j])\texttt{(nums[i], nums[j])}(nums[i], nums[j]),并满足下述条件:
- 0≤i,j<nums.length\texttt{0} \le \texttt{i, j} < \texttt{nums.length}0≤i, j<nums.length
- nums[i]≤nums[j]\texttt{nums[i]} \le \texttt{nums[j]}nums[i]≤nums[j]
- |nums[i]-nums[j]|=k\texttt{|nums[i] - nums[j]|} = \texttt{k}|nums[i] - nums[j]|=k
注意,|val|\texttt{|val|}|val| 表示 val\texttt{val}val 的绝对值。
示例
示例 1:
输入:nums=[3,1,4,1,5],k=2\texttt{nums = [3, 1, 4, 1, 5], k = 2}nums = [3, 1, 4, 1, 5], k = 2
输出:2\texttt{2}2
解释:数组中有两个 2\texttt{2}2-diff 数对,(1,3)\texttt{(1, 3)}(1, 3) 和 (3,5)\texttt{(3, 5)}(3, 5)。
尽管数组中有两个 1\texttt{1}1,但我们只应返回不同的数对的数量。
示例 2:
输入:nums=[1,2,3,4,5],k=1\texttt{nums = [1, 2, 3, 4, 5], k = 1}nums = [1, 2, 3, 4, 5], k = 1
输出:4\texttt{4}4
解释:数组中有四个 1\texttt{1}1-diff 数对,(1,2)\texttt{(1, 2)}(1, 2),(2,3)\texttt{(2, 3)}(2, 3),(3,4)\texttt{(3, 4)}(3, 4) 和 (4,5)\texttt{(4, 5)}(4, 5)。
示例 3:
输入:nums=[1,3,1,5,4],k=0\texttt{nums = [1, 3, 1, 5, 4], k = 0}nums = [1, 3, 1, 5, 4], k = 0
输出:1\texttt{1}1
解释:数组中只有一个 0\texttt{0}0-diff 数对,(1,1)\texttt{(1, 1)}(1, 1)。
数据范围
- 1≤nums.length≤104\texttt{1} \le \texttt{nums.length} \le \texttt{10}^\texttt{4}1≤nums.length≤104
- -107≤nums[i]≤107\texttt{-10}^\texttt{7} \le \texttt{nums[i]} \le \texttt{10}^\texttt{7}-107≤nums[i]≤107
- 0≤k≤107\texttt{0} \le \texttt{k} \le \texttt{10}^\texttt{7}0≤k≤107
解法
思路和算法
由于题目要求计算数组 nums\textit{nums}nums 中的不同的差为 kkk 的数对的数目,因此只需要考虑数组中有哪些数字,不需要考虑顺序。
计算差为 kkk 的数对的数目需要考虑两种情况,分别是 k=0k = 0k=0 和 k>0k > 0k>0。
当 k=0k = 0k=0 时,每个差为 kkk 的数对由两个相等的整数组成,对于任意整数 num\textit{num}num,只有当 num\textit{num}num 在数组 nums\textit{nums}nums 中出现次数大于 111 次时,才有数对 (num,num)(\textit{num}, \textit{num})(num,num)。遍历数组 nums\textit{nums}nums 并用哈希表记录每个数字的出现次数,然后遍历哈希表,对于哈希表中的每个数字,如果出现次数大于 111 次,则将数对的数目加 111。遍历哈希表结束之后即可得到差为 kkk 的数对的数目。
当 k>0k > 0k>0 时,每个差为 kkk 的数对由两个不相等的整数组成,对于任意整数 num\textit{num}num,当 num\textit{num}num 和 num+k\textit{num} + knum+k 都在数组中出现时,有数对 (num,num+k)(\textit{num}, \textit{num} + k)(num,num+k)。遍历数组 nums\textit{nums}nums 并用哈希集合记录出现的数字,然后遍历哈希集合,对于哈希集合中的每个数字 num\textit{num}num,如果 num+k\textit{num} + knum+k 也在哈希集合中,则将数对的数目加 111。遍历哈希集合结束之后即可得到差为 kkk 的数对的数目。
代码
class Solution {public int findPairs(int[] nums, int k) {int pairs = 0;if (k == 0) {Map<Integer, Integer> map = new HashMap<Integer, Integer>();for (int num : nums) {map.put(num, map.getOrDefault(num, 0) + 1);}Set<Integer> set = map.keySet();for (int num : set) {if (map.get(num) > 1) {pairs++;}}} else {Set<Integer> set = new HashSet<Integer>();for (int num : nums) {set.add(num);}for (int num : set) {if (set.contains(num + k)) {pairs++;}}}return pairs;}
}
复杂度分析
-
时间复杂度:O(n)O(n)O(n),其中 nnn 是数组 nums\textit{nums}nums 的长度。需要遍历数组一次,使用哈希表或哈希集合存储数组中的不同数字,然后遍历哈希表或哈希集合一次,由于哈希表或哈希集合中的元素个数不超过数组长度,因此时间复杂度是 O(n)O(n)O(n)。
-
空间复杂度:O(n)O(n)O(n),其中 nnn 是数组 nums\textit{nums}nums 的长度。需要使用哈希表或哈希集合存储数组中的不同数字,最坏情况下需要存储数组中的全部数字。
相关文章:

哈希表题目:数组中的 k-diff 数对
文章目录题目标题和出处难度题目描述要求示例数据范围解法思路和算法代码复杂度分析题目 标题和出处 标题:数组中的 k-diff 数对 出处:532. 数组中的 k-diff 数对 难度 4 级 题目描述 要求 给定一个整数数组 nums\texttt{nums}nums 和一个整数 k…...
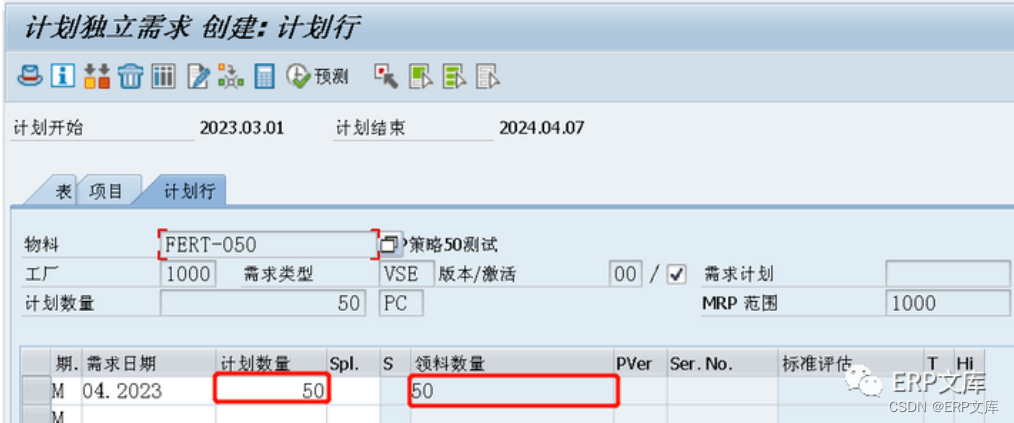
SAP ERP系统PP模块计划策略2050详解
SAP/ERP系统中面向订单生产的计划策略主要有20和50两个策略,这两个策略都是面向订单生产的计划策略,也是离散制造行业应用比较广泛的策略。它们之间最大差异就是在于20策略完全是由订单驱动,而50策略是预测加订单驱动,本文主要介绍…...

TIA博途中将硬件目录更改为中文的具体方法演示
TIA博途中将硬件目录更改为中文的具体方法演示 基本步骤可参考如下: 第一步: 第二步: 具体的操作演示: 如下图所示,在所示的目录中找到zh-chs文件夹,删除或修改文件夹的名称均可,这里建议大家修改文件夹的名称,防止以后需要恢复成英文目录, 如下...

【多线程操作】线程池模拟实现
目录 一.线程池的作用 二.线程池的模拟实现 1.线程模块(Thread.hpp): 2.线程锁模块(LockGuard.hpp): 3.任务模块(Task.hpp) 4.线程池核心(ThreadPool.hppÿ…...
HBase---Hbase安装(单机版)
Hbase安装单机版 文章目录Hbase安装单机版Master/Slave架构安装步骤配置Hbase1.上传压缩包解压更名修改hbase-env.sh修改hbase-site.xml配置HBase环境变量配置Zookeeper复制配置文件修改zoo.cfg配置文件修改myid配置Zookeeper环境变量刷信息配置文件启动hbase步骤hbase shellMa…...
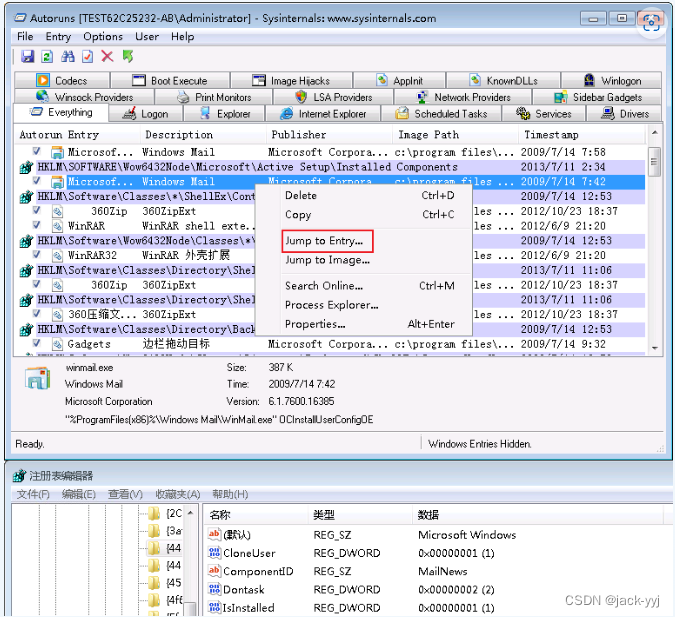
启动项管理工具Autoruns使用实验(20)
实验目的 (1)了解注册表的相关知识; (2)了解程序在开机过程中的自启动; (3)掌握Autoruns在注册表和启动项方面的功能;预备知识 注册表是windows操作系统中的一个核心数据…...

BFD单臂回声实验详解
13.1.1BFD概念 BFD提供了一个通用的、标准化的、介质无关的、协议无关的快速故障检测机制,有以下两大优点: 对相邻转发引擎之间的通道提供轻负荷、快速故障检测。 用单一的机制对任何介质、任何协议层进行实时检测。 BFD是一个简单的“Hello”协议。两个系统之间建立BFD会…...
详解JAVA类加载器
目录 1.概述 2.双亲委派 3.ServiceClassLoader 4.URLClassLoader 5.加载冲突 1.概述 概念: 类加载器(Class Loader)是Java虚拟机(JVM)的一个重要组件,负责加载Java类到内存中并使其可以被JVM执行。类…...
)
记录一些常用C标准库函数,以及Linux系统调用函数的作用(不断更新)
C标准库函数 perror() 函数 作用:perror函数是C标准库中的一种函数,用于在STDERR(标准错误输出流)中输出给定的错误信息字符串。它不属于Linux系统调用函数。 具体使用方法:perror("调用的函数名") 所需…...
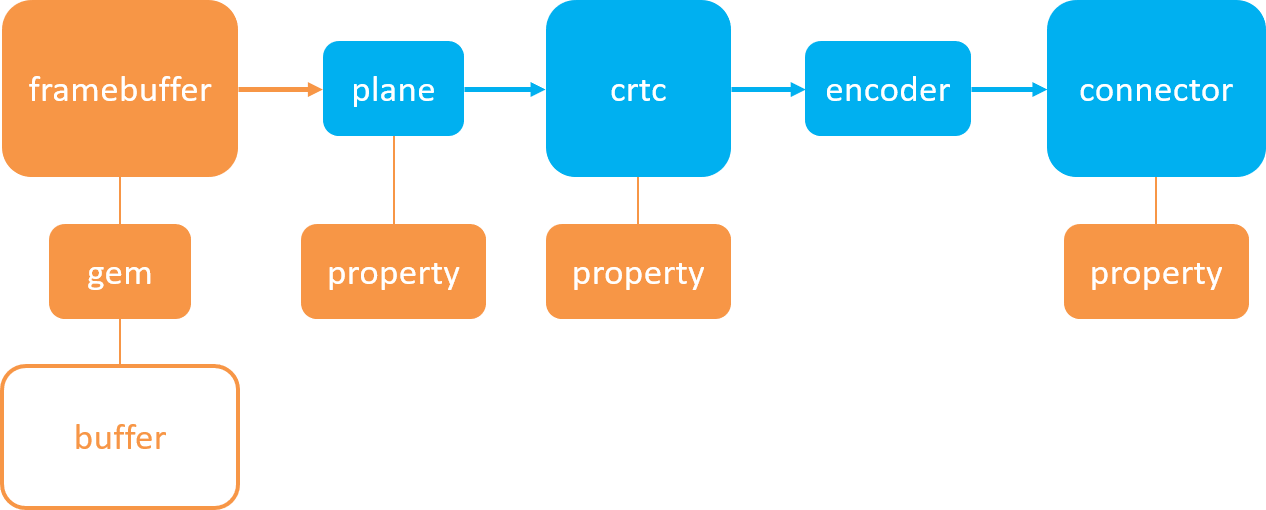
RK3568平台开发系列讲解(显示篇)DRM的atomic接口
🚀返回专栏总目录 文章目录 一、Property二、Standard Properties三、代码案例沉淀、分享、成长,让自己和他人都能有所收获!😄 📢目前DRM主要推荐使用的是 Atomic(原子的) 接口。 一、Property Property(属性)—– Atomic操作必须依赖的基本元素 Property把前面的…...

2022年MathorCup数学建模C题自动泊车问题解题全过程文档加程序
2022年第十二届MathorCup高校数学建模 C题 自动泊车问题 原题再现 自动泊车是自动驾驶技术中落地最多的场景之一,自动泊车指在停车场内实现汽车的自动泊车入位过程,在停车空间有限的大城市,是一个比较实用的功能,减少了驾驶员将…...

【需求响应】基于数据驱动的需求响应优化及预测研究(Matlab代码实现)
👨🎓个人主页:研学社的博客💥💥💞💞欢迎来到本博客❤️❤️💥💥🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密…...
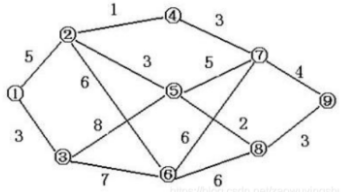
Bellman-ford和SPFA算法
目录 一、前言 二、Bellman-ford算法 1、算法思想 2、算法复杂度 3、判断负圈 4、出差(2022第十三届国赛,lanqiaoOJ题号2194) 三、SPFA算法:改进的Bellman-Ford 1、随机数据下的最短路问题(lanqiaoOJ题号1366&…...

假如你知道这样的MySQL
数据库三范式是什么? 第一范式(1NF):字段具有原子性,不可再分。(所有关系型数据库系 统都满足第一范式数据库表中的字段都是单一属性的,不可再分)第二范式(2NF)是在第一范式(1NF)的…...
SpringBoot笔记(一)入门使用
一、为什么用SpringBootSpringBoot优点创建独立Spring应用内嵌web服务器自动starter依赖,简化构建配置自动配置Spring以及第三方功能提供生产级别的监控、健康检查及外部化配置无代码生成、无需编写XMLSpringBoot缺点人称版本帝,迭代快,需要时…...
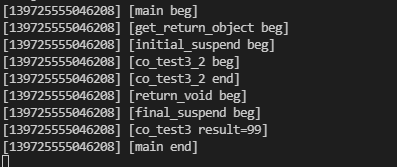
C++20 协程体验
1 介绍协程是比线程更加轻量级并发编程方式,CPU资源在用户态进行切换,CPU切换信息在用户态保存。协程完成异步的调用流程,并对用户展示出同步的使用方式。协程的调度由应用层决定,所以不同的实现会有不同的调度方式,调度策略比较灵…...

这三个小事你做HIGG FEM时要知道
【这三个小事你做HIGG FEM时要知道】1.为什么做了Higg FEM 自评后要做验证?「自评 验证」Higg FEM 是一个持续改善的框架方法,来帮助工厂实现持续的环保改善,是一个最基本的要求,如果工厂期望得到一个更加客观的评价,…...

.net6 wpf程序一个内存不断增长问题的解决方法
一个.net6的应用程序,底层不断采集数据。使用wpf制作了一个简单的界面显示数据接收的情况。程序中引用了 Material Design UI框架。当程序长时间运行时发现内存在不断增长。一个星期后工作集占用内存达到1GB。使用dotnet-dump工具收集内存使用情况,并且分…...
NICEGUI---ROS开发之中常用的GUI工具
0. 简介 对于ROS来说,如果不具备一定知识的人员来使用这些我们写的算法,如果说没有交互,这会让用户使用困难,所以我们需要使用GUI来完成友善的数据交互,传统的GUI方法一般有PYQT这类GUI方法,但是这类GUI工…...

高盐废水除钙镁的技术解析
高盐废水指含有机物和至少总溶解固体(totaldissolvedsolids,tds)的质量分数大于3.5%的废水,具有水量大,无机盐离子k、na、ca2、mg2、cl-、so42-等含量高,水质水量变化大,成分复杂,难生化降解等特…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...
