蓝桥杯-算法-印章问题
这个题真的顶啊!
思路:
n种图案,m张印章,每一个图案的概率是1/n,这个概率以后用P表示
首先我们定义dp[i][j]是买了i张印章(对应于上面的m),凑齐j种图案的概率(对应于上面的n)
然后是推导:
1.如果i<j的话,说明无论买多少印章,都不能凑齐j种图案,所以概率我们就知道是0,所以二维数组dp[i][j]=0
2.如果j=1,说明买i张印章,凑齐一种的概率
这里分成两种情况讨论。
①如果j=1,说明,买一张凑齐一种的概率,这个概率肯定是1
②如果j>1,说明买j张,凑齐一种的概率是多少。
这里详细点,想一想哈,我们如果买两章,也就是j=2,我们凑齐一种的概率是不是应该这样想:p*p*n。这里的思路是:我们要凑齐一种的概率,但是我们抽了两张,每一张的概率是不是p,两张的概率是不是p*p。但是为什么乘n呢,这样想哈,我们一共有n种印章,每一种的概率是不是都是一样的,所以凑齐的这一个就有可能是n中印章的任意一种。所以得乘一个n
3.接下来是普遍情况了。
我们凑得印章都是随机的,我们买之前是不知道下一个是哪种类别的
所以,如果下一张是之前已经存在过得印章的话(也就是前面买的i-1张已经凑齐了j种,接下来的第i张就是重复前面的印章了),所以这个重复的印章再被抽取的时候,它的概率就是j*p(再详细点,前面已经有了j种了,我们此时假设的是,与之前的重复了,而与每一个重复的概率都是p,所以这里是j*p)
这里的式子是:
dp[i][j] = dp[i-1][j] * (j/n) = dp[i-1][j] *(j*p)
4.然后再就是抽取的印章不是重复的情况了
这个说明前i-1张我们凑齐了j-1种,而第i张,也就是接下来的这一张就是要凑齐的一种,但是我们不确定这一个出现的是没出现印章中的哪一种(有点儿绕,慢慢想一下)。因为前面已经出现了j-1种,所以还有n-(j-1)种没有出现。而接下来的这个只要是这没有出现的一种就行了,这个时候凑齐这一种的概率就是(n-j+1)*p
这里的式子就是:
dp[i][j] = dp[i-1][j-1]*(n-(j-1))/n = dp[i-1][j-1]*(n-j+1)*p
所以对于dp[i][j]这里的情况,就是3,4两种情况相加了。
代码是借鉴的其余博客,未亲自编写
#include<stdio.h>
#include<math.h>
#include<algorithm>
#include<string.h>
#include<iostream>
using namespace std;
double dp[30][30];
int main(void)
{
int n,m;
cin>>n>>m;
double p=1.0/n;
memset(dp,0,sizeof(dp));
for(int i=1;i<=m;i++)//i张印章
{
for(int j=1;j<=n;j++)//j种图案
{
if(i<j)//不可能凑齐
{
dp[i][j]=0;
}
if(j==1)//j只要所有图案中的一种就可以了,所以我们(1/n)^i还要再乘n,就是p^i-1
{
dp[i][j]=pow(p,i-1);
}
else//买了i张凑齐j种,第i张 要么和之前凑齐的一样,要么不一样
{
dp[i][j]=dp[i-1][j]*(j*p)+dp[i-1][j-1]*(n-j+1)*p;
}} }
printf("%.4lf\n",dp[m][n]);
return 0;
} 相关文章:

蓝桥杯-算法-印章问题
这个题真的顶啊!思路:n种图案,m张印章,每一个图案的概率是1/n,这个概率以后用P表示首先我们定义dp[i][j]是买了i张印章(对应于上面的m),凑齐j种图案的概率(对应于上面的n…...

戴尔游匣G16电脑U盘安装系统操作教程分享
戴尔游匣G16电脑U盘安装系统操作教程分享。有用户在使用戴尔游匣G16电脑的时候遇到了系统问题,比如电脑蓝屏、自动关机重启、驱动不兼容等问题。遇到这些问题如果无法进行彻底解决,我们可以通过U盘重新安装系统的方法来解决,因为这些问题一般…...

2023数学建模美赛赛题思路分析 2023美赛 美国大学生数学建模数模
将在本帖更新2023美国大学生数学建模数模美赛各个赛题思路,大家可以点赞收藏! 一、参赛报名 组队参赛(每队人数3人,专业不限)。 二、赛题思路及资料 会在本帖更新思路分析,Q群可领取模型代码/赛题思路资料…...

vue3与vue2的对比
Vue 3.0 和 Vue 2.0 是 Vue 前端框架的两个主要版本,它们有着不同的更新和优化: Vue 3.0 主要更新内容: 采用 TypeScript 作为开发语言,提高了代码的类型安全性。 速度更快,内存使用更少,支持大规模数据处…...
备战金三银四)
史上最全软件测试工程师常见的面试题总结(百度、oppo、中软国际、华为)备战金三银四
1、面试:神州数码1.介绍你下你项目中一个自动化实现的流程2.你觉得做自动化的意义在哪里 >需要对之前已经实现的功能进行回归测试、保证当前版本更新的内容不能影响到之前已经实现好的功能3.你们做自动化产生了什么结果 >测试报告、报错截图和报错日志、测试报…...
“深度学习”学习日记。卷积神经网络--用CNN的实现MINIST识别任务
2023.2.11 通过已经实现的卷积层和池化层,搭建CNN去实现MNIST数据集的识别任务; 一,简单CNN的网络构成: 代码需要在有网络的情况下运行,因为会下载MINIST数据集,运行后会生成params.pkl保留训练权重&…...

JavaWeb--JDBC练习
JDBC练习5.1 需求5.2 案例实现5.2.1 环境准备5.2.2 查询所有5.2.3 添加数据5.2.4 修改数据5.2.5 删除数据5.1 需求 完成商品品牌数据的增删改查操作 查询:查询所有数据添加:添加品牌修改:根据id修改删除:根据id删除 5.2 案例实…...

【LeetCode】2335. 装满杯子需要的最短总时长
2335. 装满杯子需要的最短总时长 题目描述 现有一台饮水机,可以制备冷水、温水和热水。每秒钟,可以装满 2 杯 不同 类型的水或者 1 杯任意类型的水。 给你一个下标从 0 开始、长度为 3 的整数数组 amount ,其中 amount[0]、amount[1] 和 a…...

Android 12.0 通过驱动实现禁用usb鼠标和usb键盘功能
1.1概述 在12.0的系统产品定制化开发中,在进行定制中有关于usb键盘和usb鼠标的需求中,产品要求禁止usb口挂载usb鼠标和usb键盘,所以需要要求在usb挂载类型的时候 判断如果是usb鼠标和usb键盘就不让挂载,这就需要从驱动方面入手来解决这个问题,接下来看下驱动的某些挂载usb…...
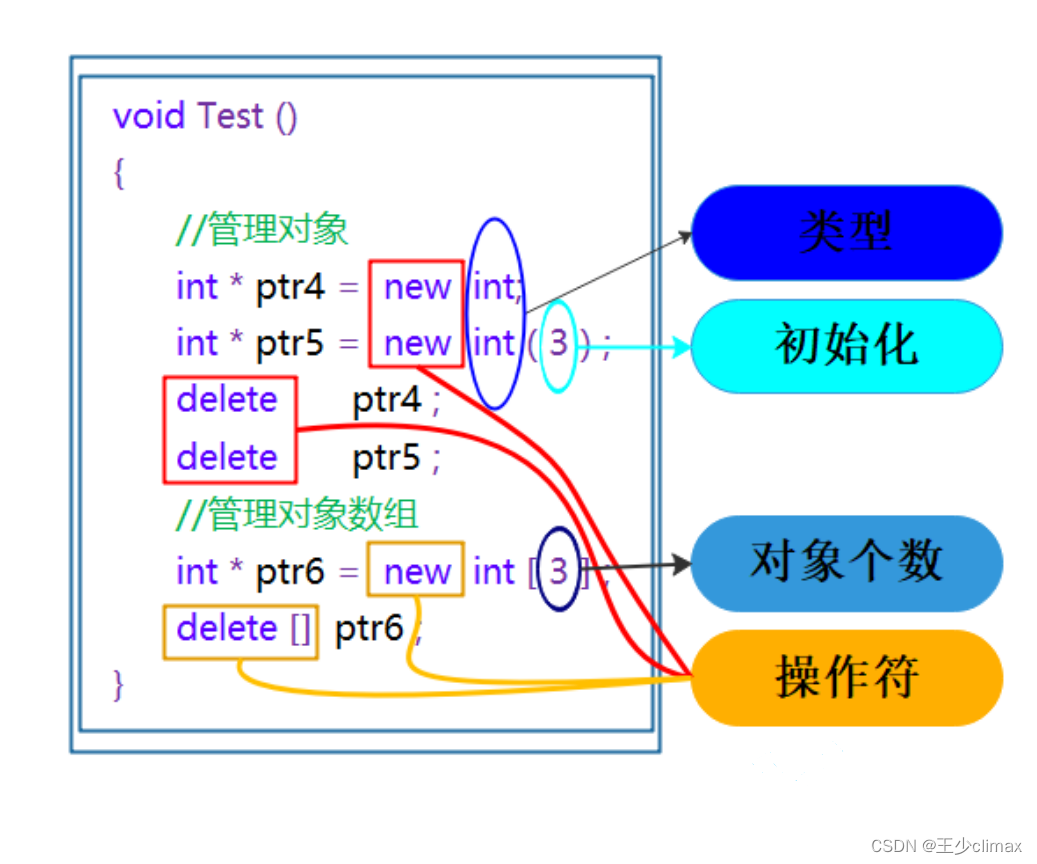
C++入门——内存管理
C入门——内存管理 C/C内存分布 分类是为了更好的管理 int globalVar 1; static int staticGlobalVar 1; void Test() {static int staticVar 1;int localVar 1;int num1[10] {1, 2, 3, 4};char char2[] "abcd";char* pChar3 "abcd";int* ptr1 (…...
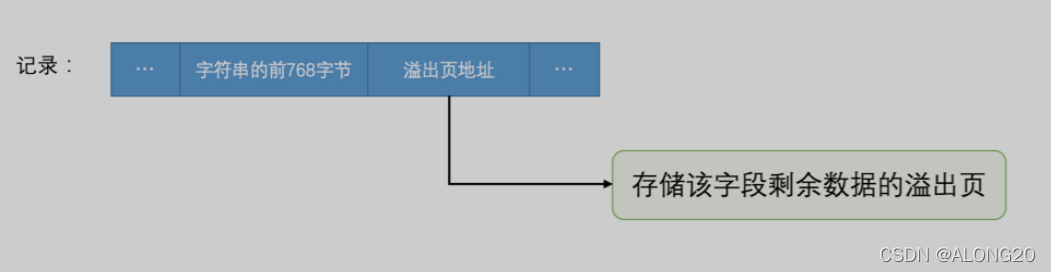
MySQL-InnoDB行格式浅析
简介 我们知道读写磁盘的速度非常慢,和内存读写差了几个数量级,所以当我们想从表中获取某些记录时, InnoDB 存储引擎需要一条一条的把记录从磁盘上读出来么? 不,那样会慢死,InnoDB 采取的方式是:…...
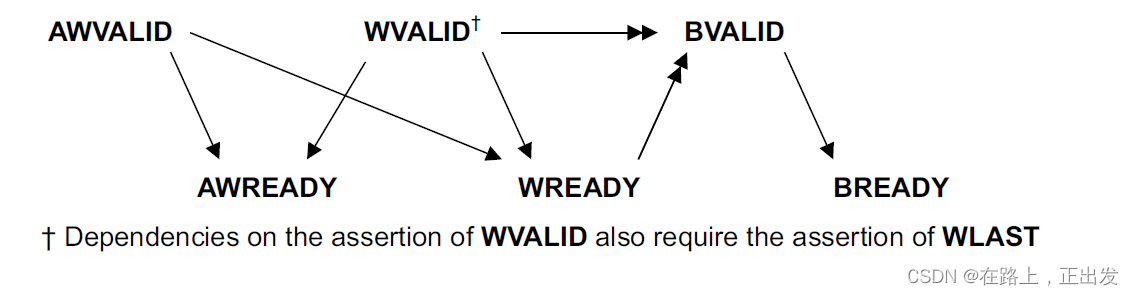
AXI 总线协议学习笔记(4)
引言 前面两篇博文从简单介绍的角度说明了 AXI协议规范。 AXI 总线协议学习笔记(2) AXI 总线协议学习笔记(3) 从本篇开始,详细翻译并学习AXI协议的官方发布规范。 文档中的时序图说明: AXI指࿱…...

C++复习笔记6
1.String类的实现 注意深浅拷贝, C语言字符串拼接函数strcat() #define _CRT_SECURE_NO_WARNINGS #include<iostream> #include<vld.h> #include<assert.h> using namespace std;class String {friend ostream& operator<<(ostream &am…...
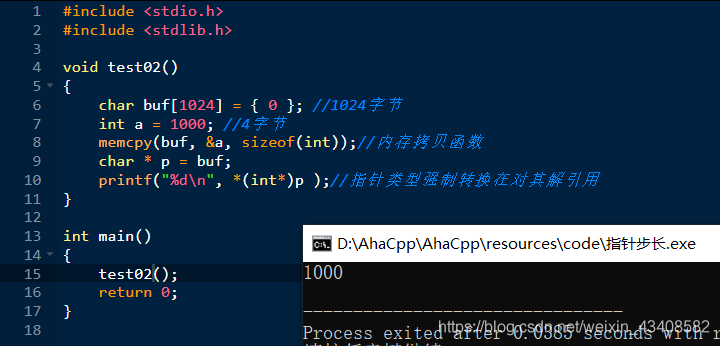
指针的步长及意义(C语言基础)
指针的步长及意义 文章目录指针的步长及意义指针变量1后偏移的字节数不同指针解引用时取出的字节数不同其他例子不同类型的指针有何不同的意义指针变量1后跳跃字节数量不同解引用的时候,取出字节数量不同 指针变量1后偏移的字节数不同 代码演示:&#…...
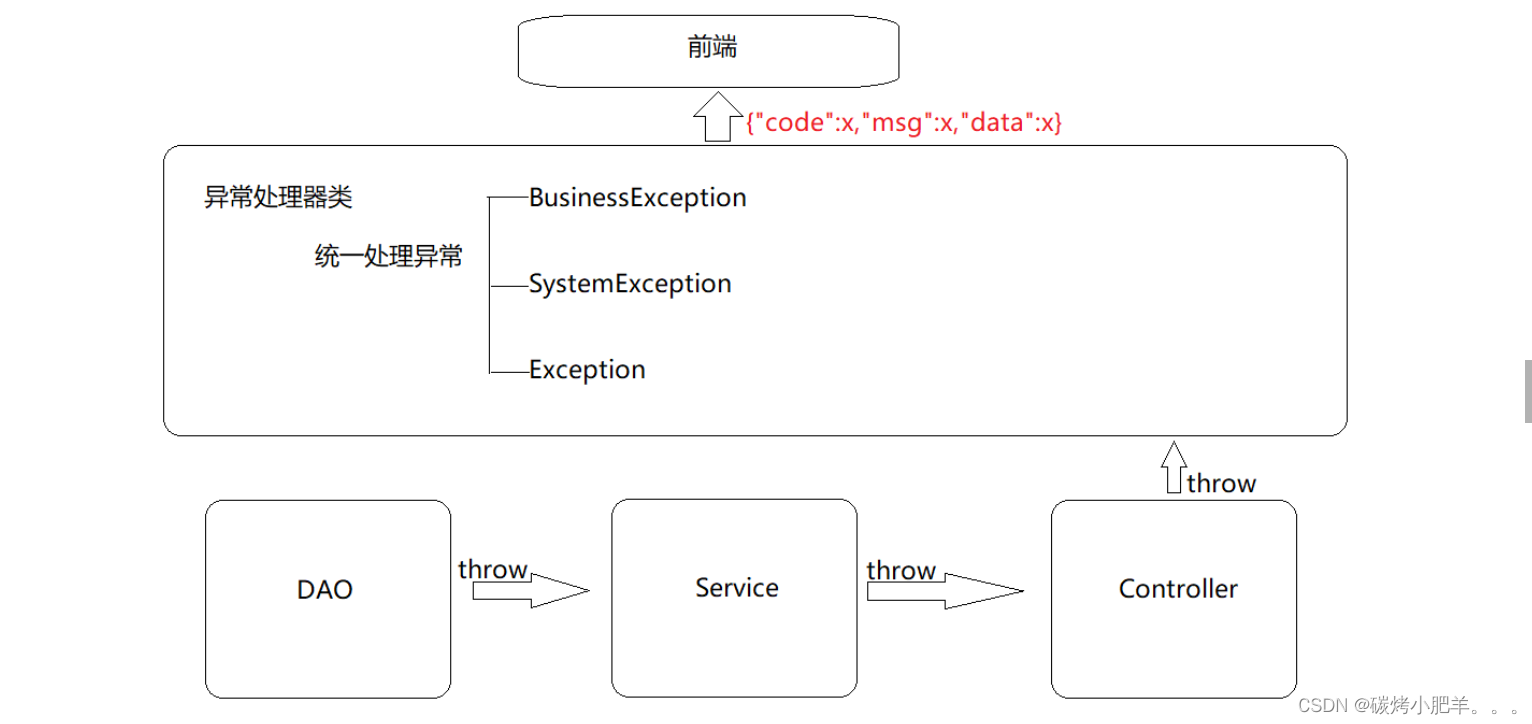
SpringMVC:统一异常处理(11)
统一异常处理1. 说明2. 问题描述3. 异常处理器使用3.1 创建异常处理器类3.2 让程序抛出异常3.3 测试4. 项目异常处理方案4.1 异常分类4.2 异常解决方案4.3 异常解决方案的具体实现4.4 测试5. 总结1. 说明 \quad本篇文章是在文章SpringMVC:SSM整合(Spring…...
SpringBoot的配置与使用
SpringBoot简介 我们的Spring是包含了众多工具的IoC容器,而SpringBoot则是Spring的加强版,可以更加方便快捷的使用 如果Spring是手动挡的车,那么SpringBoot就是自动挡的车,让我们的驾驶体验变得更好 SpringBoot具有一下几种特征…...
【Python】tkinter messagebox练习笔记
我一好友在朋友圈看到人家用代码花式秀恩爱,让我也做一个,我就用我学习半年python的功力,做了这一个东西。🙏窗口主页面(图一)为了让我这个盆友有颜面,特意做了一个问答问他帅不帅,以…...
答案解析)
2022年12月电子学会Python等级考试试卷(五级)答案解析
青少年软件编程(Python)等级考试试卷(五级) 分数:100 题数:38 一、单选题(共25题,共50分) 1. 下面哪个语句正确定义了元组类型数据tuple1?( ) A. t…...
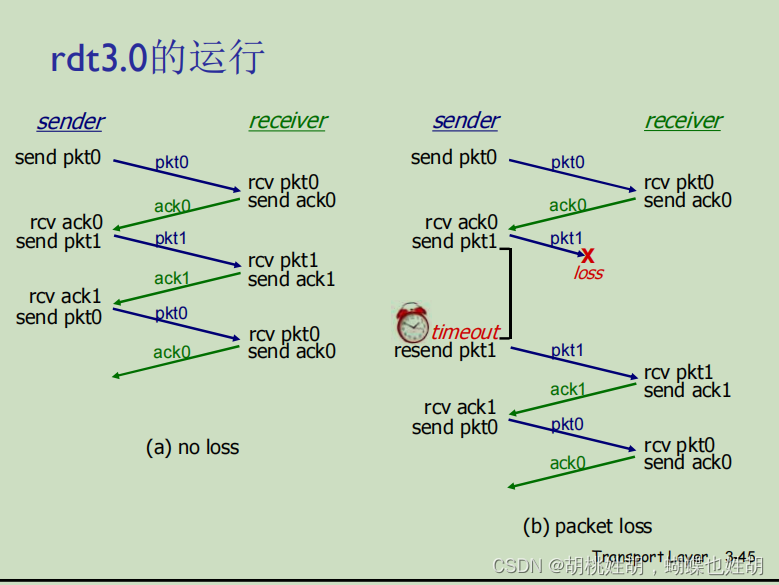
计算机网络自定向下 -- 浅谈可靠性之rdt协议
可靠性数据传输原理 可靠指数据在传输过程中不错,不丢,不乱 运输层要为应用层提供一种服务:数据可以通过一条可靠的信道进行传输,在该信道中传输的数据不会受到损坏或者丢失, 实现这种服务的是可靠数据传输协议。 要实现这种服…...
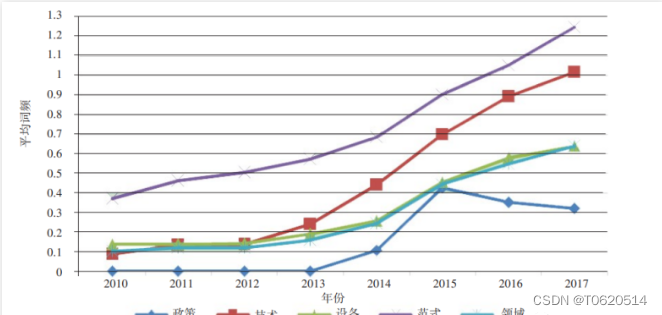
制造业升级转型:制造业上市公司-智能制造词频统计数据集
发展智能制造,关乎中国制造业转型升级的成效。基于中国制造业上市公司年报,通过文本数据挖掘,提取关键词反映企业对智能制造的关切焦点,进而运用词频及共词网络分析,洞察中国智能制造的发展态势。 研究发现࿰…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...
