git版本回退简单记录
简单记录git版本回退的命令,参考的是这篇文章1
首先查看以前存档的版本:
git log
1. 知道要回退的版本和现在的版本差了多少代
回退上一代版本(1个以前)
git reset –hard HEAD^
回退上上一代版本(2个以前)
git reset –hard HEAD^^
回退n代以前的版本
以100个以前的版本为例:
git reset –hard HEAD~100
2. 不知道要回退的版本和现在的版本差了多少代
这时候要知道版本号,我们使用命令:
git reflog
查看版本号,比如已知版本号35d0053,我们可以回退至版本号:
git reset –hard 35d0053
git的版本回退教程(带你一步一步操作) ↩︎
相关文章:

git版本回退简单记录
简单记录git版本回退的命令,参考的是这篇文章1 首先查看以前存档的版本: git log1. 知道要回退的版本和现在的版本差了多少代 回退上一代版本(1个以前) git reset –hard HEAD^回退上上一代版本(2个以前࿰…...
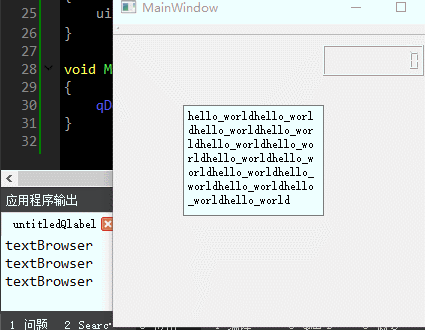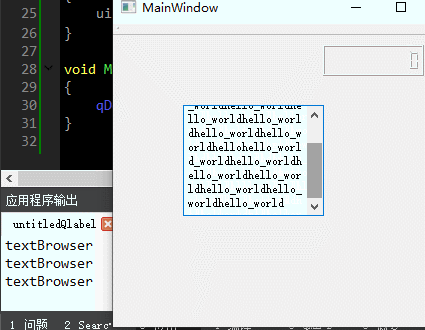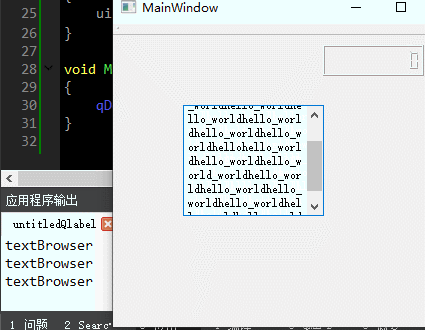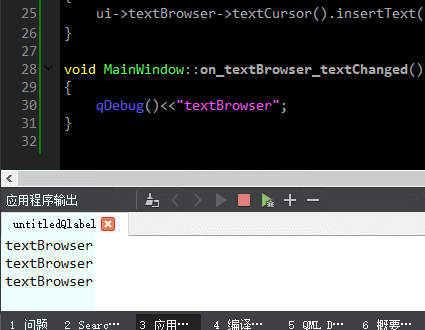
QT入门Display Widgets之QLine、QLcdNumber、QTextBrowser
目录 一、QLine界面相关 1、布局介绍 2、界面基本属性 二、QLCDNumber的介绍 1、界面布局 2、定时器代码测试 三、QTextBrowser 此文为作者原创,创作不易,转载请标明出处! 一、QLine界面相关 1、布局介绍 先看下界面中创建个Q…...

Spring学习笔记
目录1 IOC容器1.1 概念1.2 IOC的底层原理1.3 Spring中IOC容器的两种实现方式(两个接口)1.3.1 BeanFactory接口1.3.2 ApplicationContext接口1.3.3 为什么开发中使用ApplicationContext接口1.3.4 ApplicationContext接口的两个实现类1.4 IOC操作之bean管理1.4.0 bean是什么&…...

数据的标准化处理
假设各个指标之间的水平相差很大,此时直接使用原始指标进行分析时,数值较大的指标,在评价模型中的绝对作用就会显得较为突出和重要,而数值较小的指标,其作用则可能就会显得微不足道。 因此,为了统一比较的标…...

性能优化|记一次线上OOM问题处理
概述最近线上监控发现 OOM 涨幅较大,因此去尝试定位和修复这个问题,在修复了一些内存泄漏和大对象占用问题后, OOM 依旧未达到正常标准,在这些新上报的 hprof 文件中,发现几乎所有 case 中都有个叫 FinalizerReference 的对象&…...

Vue动态粒子特效插件(背景线条吸附动画)
目录 效果图: 一、安装: 二、引入 main.js 文件: 三、使用: 四、属性说明: 效果图: 一、安装: npm install vue-particles --save 二、引入 main.js 文件: import VueParticles…...

【Java 类】002-类、属性、方法、代码块
【Java 类】002-类、属性、方法、代码块 文章目录【Java 类】002-类、属性、方法、代码块一、类1、类与对象2、类的作用3、创建与使用类类结构创建类调用类运行结果4、Java 类的执行过程5、封装、继承、多态、抽象类、内部类、接口、枚举、记录、注解等二、属性1、概述2、类型3…...

Ubuntu Linux 编译安装的基本步骤
文章目录1 基本步骤若报错: No such file or directory2 解压 tar.bz2文件参考:1 基本步骤 解压: tar -zxvf file.tar.gz 进入解压后的文件夹: cd file 源码编译安装 ./configure # ./configmakesudo make install 若报错&…...
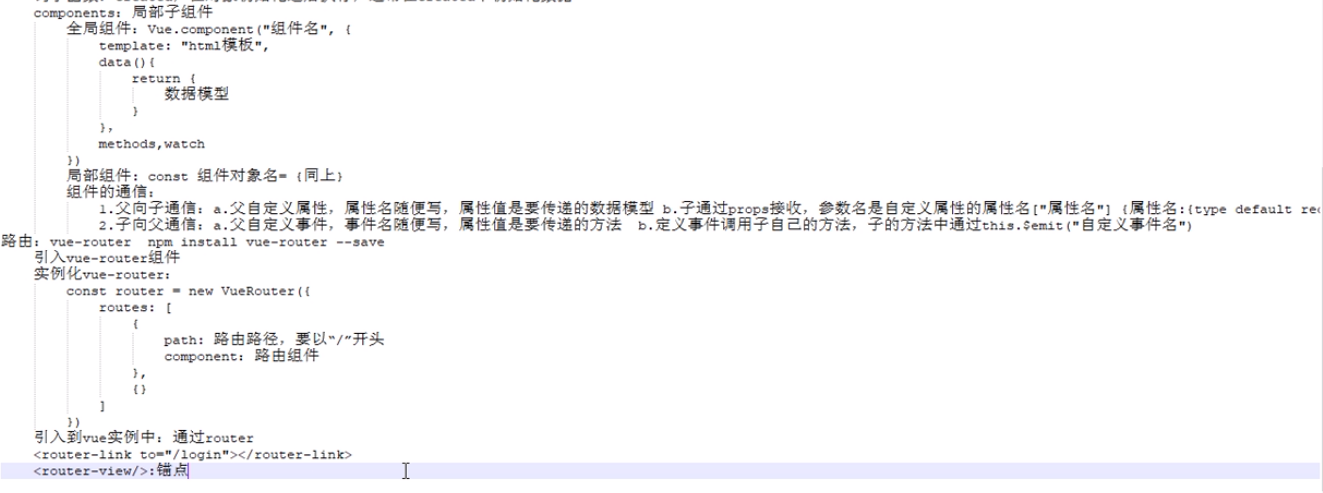
day59反刍笔记
1.本地环境安装vue后,没有vue.js文件,只有vue.cjs.js文件, 引用后也无法正常使用,看npm install vue后的文件夹中没有vue.js文件_找不到vue.js_一枝风的博客-CSDN博客 老哥的博客后得到启发,将原本的命令由࿱…...

【阅读笔记】你不知道的Javascript--强制类型转换4
目录强制类型转换基本概念JSONboolean强转归纳其他知识点被诟病的安全使用隐式强转法则抽象关系比较语法表达式变动强制类型转换 基本概念 类型转换发生在静态类型语言的编译阶段; 强制类型转换则发生在动态类型语言的运行时(runtime) JSON…...
)
华为OD机试真题Python实现【有效子字符串】真题+解题思路+代码(20222023)
有效子字符串 题目 输入两个字符串S和L,都只包含小写字母, S长度 <= 100,L长度 <= 500000, 判断S是否是L的有效子字符串, 判定规则:S中的每个字符在L中都能找到(可以不连续) 且S在L中字符的前后顺序与S中顺序要保持一致 例如: S="ace"是L="abcd…...
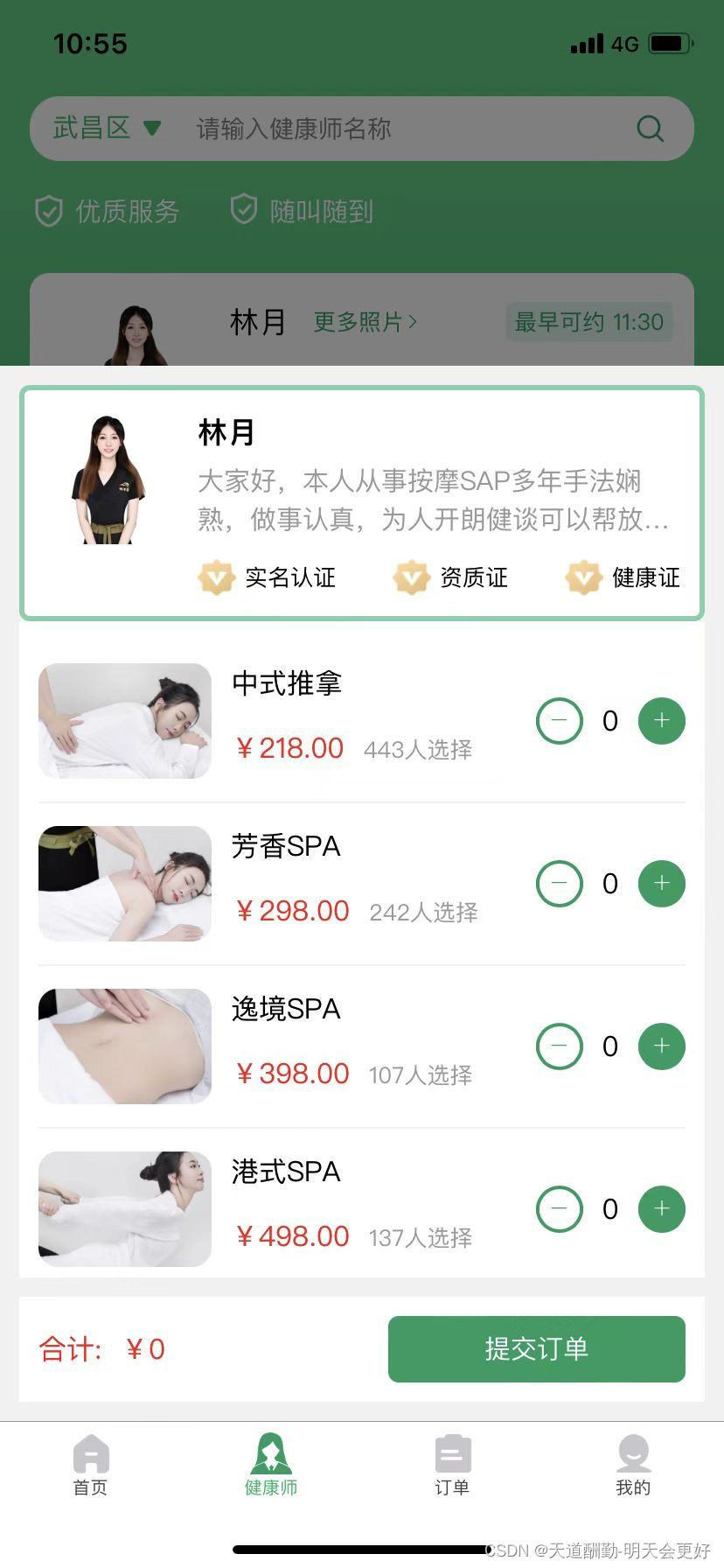
上门按摩预约APP源码-东郊到家源码(开发,PHP,平台搭建)
一、什么是上门按摩预约APP源码? 上门按摩预约APP源码是一款家政服务类型的APP,可以帮忙用户在家就能享受按摩的服务。APP源码分两端,一端是用户端,另外一端是技师端。采用的技术,前端是安卓IOS,后端是PHP&…...
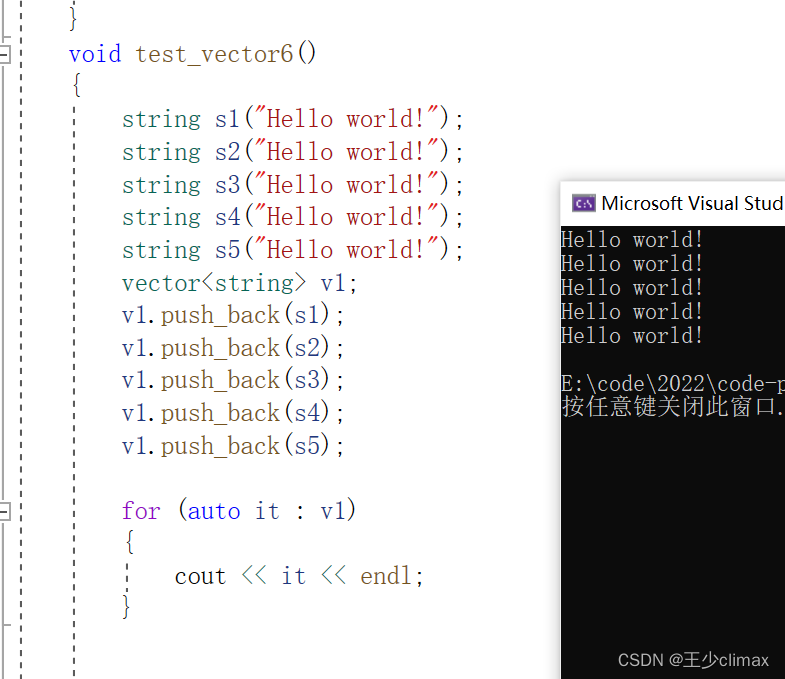
STL讲解——模拟实现vector
STL讲解——模拟实现vector vector深度剖析 在STL源码中,发现vector定义的并不是 start、size、capacity,而是start、finish、end_of_storage. 这样就可以得到size()和capacity()。 sizefinish-start capacityend_of_storage-start 扩容可能是本地扩容也…...

各种经典排序算法介绍及实现源码
一,冒泡排序(Bubble Sort) 排序算法是程序员必须了解和熟悉的一类算法,排序算法有很多种,基础的如:冒泡、插入、选择、快速、归并、计数、基数和桶排序等。 冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较,看是否满足大小关系要求,如果不…...

历史大讲堂:这是真·图形化 苹果系统历史回顾(上)
众所周知,米国有个非常牛掰的公司叫苹果,想必大家对这个logo不陌生吧。 目前已发布的苹果产品有iPhone、iPad、iPod等等,简直花样繁多,而且各种功能很好用,我的手机就是一部苹果iPhone X。 等一下,似乎扯远…...
今天女神节,用python画个贺卡送给母亲吧
今天女神节,你给女神妈妈准备了什么祝福呢?如果还没有,那么画个贺卡送给她吧,在你眼里,她是一个什么样的人呢? 是"可爱",“温柔”,“美丽”,“漂亮”…...
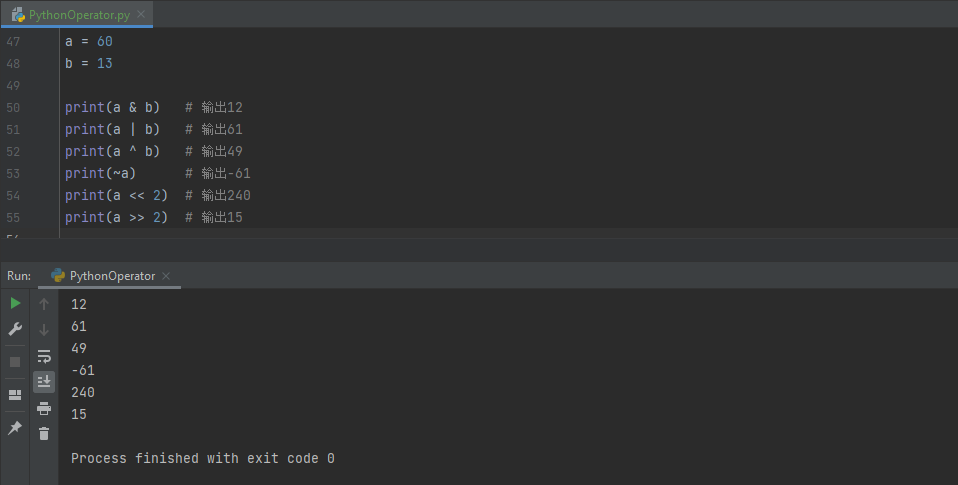
【编程基础之Python】11、Python中的表达式
【编程基础之Python】11、Python中的表达式Python中的表达式表达式与运算符算术表达式赋值表达式比较表达式逻辑表达式位运算表达式总结Python中的表达式 在Python中,表达式是由操作数、运算符和函数调用等组成的语法结构,可以进行各种数学运算、逻辑判…...
)
华为OD机试真题Python实现【乱序整数序列两数之和绝对值最小】真题+解题思路+代码(20222023)
乱序整数序列两数之和绝对值最小 题目 给定一个随机的整数数组(可能存在正整数和负整数)nums, 请你在该数组中找出两个数,其和的绝对值(|nums[x]+nums[y]|)为最小值 并返回这两个数(按从小到大返回)以及绝对值。 每种输入只会对应一个答案。但是,数组中同一个元素不能使用两…...
(python))
字符串转换整数 (atoi)(python)
链接: https://leetcode.cn/problems/string-to-integer-atoi 题目描述: 请你来实现一个 myAtoi(string s) 函数,使其能将字符串转换成一个 32 位有符号整数(类似 C/C 中的 atoi 函数)。 函数 myAtoi(string s) 的算法…...

洛谷 P1115 最大子段和
题目链接:P1115 最大子段和 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 题目描述 给出一个长度为 n 的序列 a,选出其中连续且非空的一段使得这段和最大。 输入格式 第一行是一个整数,表示序列的长度 n。 第二行有 n 个整数ÿ…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...
