贪心算法问题
分发饼干-455
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。对每个孩子 i ,都有一个胃口值 gi ,这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j ,都有一个尺寸 sj 。如果 sj >= gi ,我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
注意:
你可以假设胃口值为正。
一个小朋友最多只能拥有一块饼干。
示例 1:输入: [1,2,3], [1,1]输出: 1解释:
你有三个孩子和两块小饼干,3个孩子的胃口值分别是:1,2,3。
虽然你有两块小饼干,由于他们的尺寸都是1,你只能让胃口值是1的孩子满足。
所以你应该输出1。
示例 2:输入: [1,2], [1,2,3]输出: 2解释:
你有两个孩子和三块小饼干,2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2.把饼干和孩子的需求都排序好,然后从最小的饼干分配给需求最小的孩子开始,不断的尝试新的饼干和新的孩子,这样能保证每个分给孩子的饼干都恰到好处的不浪费,又满足需求。
利用双指针不断的更新 i 孩子的需求下标和 j饼干的值,直到两者有其一达到了终点位置:
- 如果当前的饼干不满足孩子的胃口,那么把
j++寻找下一个饼干,不用担心这个饼干被浪费,因为这个饼干更不可能满足下一个孩子(胃口更大)。 - 如果满足,那么
i++; j++; count++记录当前的成功数量,继续寻找下一个孩子和下一个饼干。
/*** @param {number[]} g* @param {number[]} s* @return {number}*/
let findContentChildren = function (g, s) {g.sort((a, b) => a - b)s.sort((a, b) => a - b)let i = 0let j = 0let count = 0while (j < s.length && i < g.length) {let need = g[i]let cookie = s[j]if (cookie >= need) {count++i++j++} else {j++}}return count
}相关文章:

贪心算法问题
分发饼干-455 假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。对每个孩子 i ,都有一个胃口值 gi ,这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j ,都有…...

深入理解 @Transactional 注解在 Spring 中的应用
前言:在 Java 开发中,事务管理是非常重要的一环。Spring 框架提供了Transactional注解来简化事务管理的操作,本文将深入介绍Transactional注解的用法,并结合代码示例进行详细讨论。 1.Transactional 注解简介 Transactional注解是…...

Python爬虫之爬取网页图片
当我们想要下载网页的图片时,发现网页的图片太多了,无从下手,那我们写一个脚本来爬取呗。 这次的脚本是专门针对某个外国网站使用的,因此仅供参考思路。 在测试的过程中,我发现网站使用了发爬虫机制,具体就…...

AI Agent(LLM Agent)入门解读
1. 什么是AI Agent? AI Agent可以理解为一个智能体,包括感知模块、规划决策模块和行动模块,类似于人类的五官、大脑和肢体。它能帮助人类处理复杂的任务,并能根据环境反馈进行学习和调整。 五官可以理解为感知模块,大…...

自动化面试常见算法题!
1、实现一个数字的反转,比如输入12345,输出54321 num 12345 num_str str(num) reversed_num_str num_str[::-1] reversed_num int(reversed_num_str) print(reversed_num) # 输出 54321代码解析:首先将输入的数字转换为字符串ÿ…...
CCF-CSP真题202206-2《寻宝!大冒险!》
题目背景 暑假要到了。可惜由于种种原因,小 P 原本的出游计划取消。失望的小 P 只能留在西西艾弗岛上度过一个略显单调的假期……直到…… 某天,小 P 获得了一张神秘的藏宝图。 问题描述 西西艾弗岛上种有 n 棵树,这些树的具体位置记录在…...
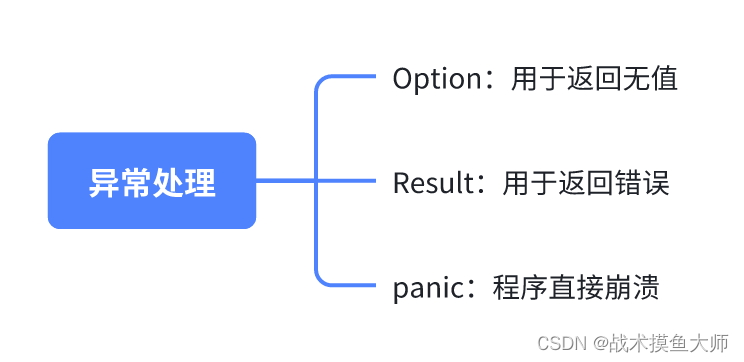
Rust编程(三)生命周期与异常处理
生命周期 生命周期,简而言之就是引用的有效作用域。在大多数时候,我们无需手动的声明生命周期,因为编译器可以自动进行推导。生命周期的主要作用是避免悬垂引用,它会导致程序引用了本不该引用的数据: {let r;{let x …...
【办公类-21-11】 20240327三级育婴师 多个二级文件夹的docx合并成docx有页码,转PDF
背景展示:有页码的操作题 背景需求: 实操课终于全部结束了,把考试内容(docx)都写好了 【办公类-21-10】三级育婴师 视频转文字docx(等线小五单倍行距),批量改成“宋体小四、1.5倍行…...
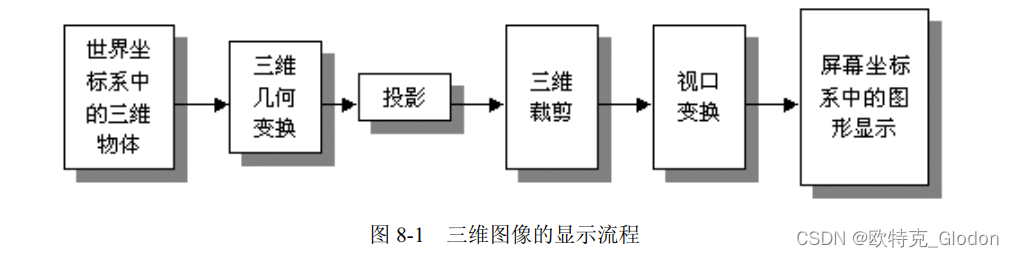
OSG编程指南<二十一>:OSG视图与相机视点更新设置及OSG宽屏变形
1、概述 什么是视图?在《OpenGL 编程指南》中有下面的比喻,从笔者开始学习图形学就影响深刻,相信对读者学习场景管理也会非常有帮助。 产生目标场景视图的变换过程类似于用相机进行拍照,主要有如下的步骤: (1)把照相机固定在三脚架上,让它对准场景(视图变换)。 (2)…...

Laplace变换-3
回忆#常见函数的Laplace变换: t z − 1 ↦ Γ ( z ) s z t^{z-1} \mapsto \frac{\Gamma(z)}{s^{z}} tz−1↦szΓ(z) (要求 R e ( z ) > 0 \mathrm{Re}(z)>0 Re(z)>0) e a t ↦ 1 s − a e^{at} \mapsto \frac{1}{s-a} eat↦s−a1…...
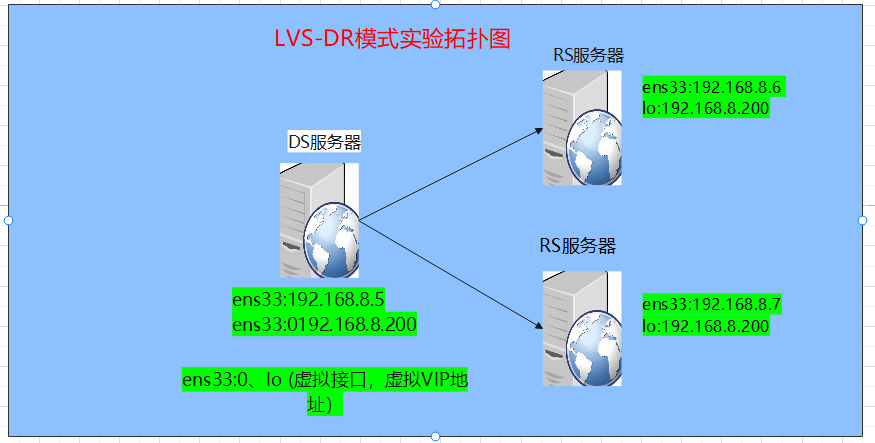
LVS负载均衡-DR模式配置
LVS:Linux virtual server ,即Linux虚拟服务器 LVS自身是一个负载均衡器(Director),不直接处理请求,而是将请求转发至位于它后端的真实服务器real server上。 LVS是四层(传输层 tcp/udp)负载均衡…...
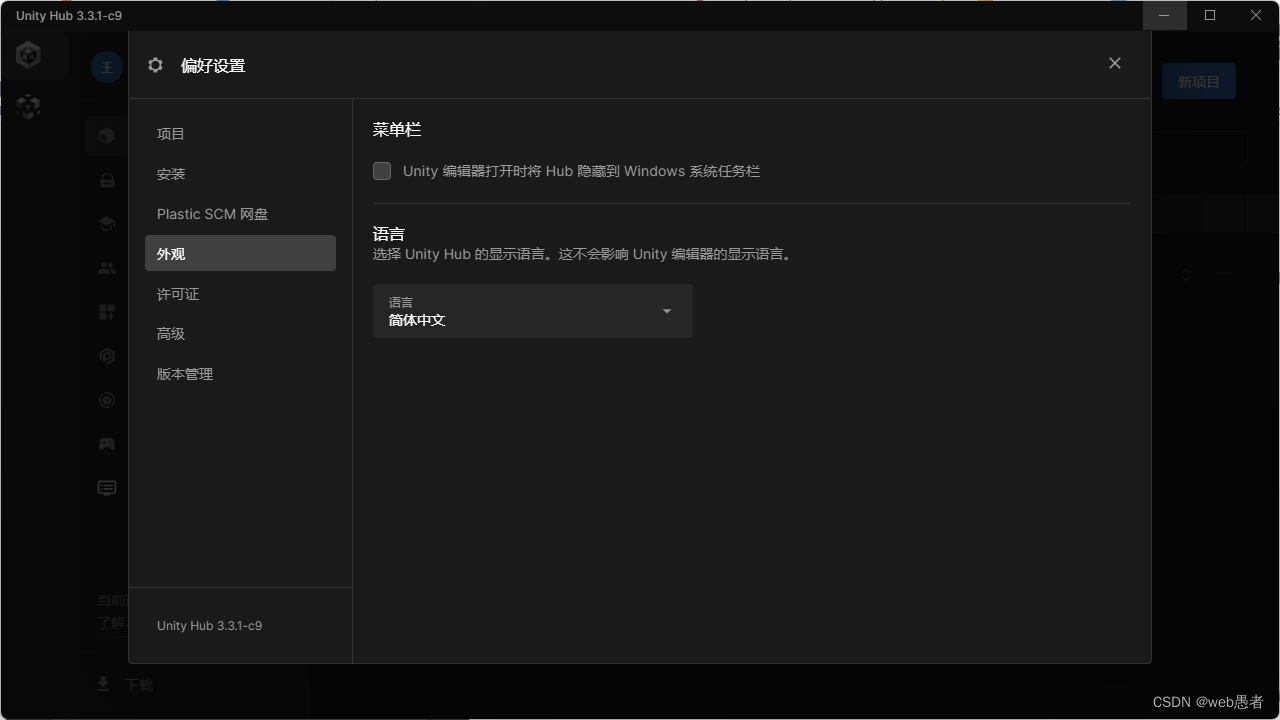
【unity】如何汉化unity Hub
相信大家下载安装unity后看着满操作栏的英文,英文不好的小伙伴们会一头雾水。但是没关系你要记住你要怎么高速运转的机器进入中国,请记住我给出的原理,不懂不代表不会用啊。现在我们就来把编译器给进行汉化。 第一步:我们打开Uni…...

【算法】KMP-快速文本匹配
文章目录 一、KMP算法说明二、详细实现1. next数组定义2. 使用next加速匹配3. next数组如何快速生成4. 时间复杂度O(mn)的证明a) next生成的时间复杂度b) 匹配过程时间复杂度 三、例题1. [leetcode#572](https://leetcode.cn/problems/subtree-of-another-tree/description/)2.…...

多维数组和交错数组笔记
1.) 关于数据的几个概念: Rank,即数组的维数,其值是数组类型的方括号之间逗号个数加上1。 Demo:利用一维数组显示斐波那契数列F(n) F(n-1) F(n-2) (n >2 ),每行显示5项,20项. static void Main(string[] args){int[] F n…...

Python(django)之单一接口展示功能前端开发
1、代码 建立apis_manage.html 代码如下: <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><title>测试平台</title> </head> <body role"document"> <nav c…...

【大模型】非常好用的大语言模型推理框架 bigdl-llm,现改名为 ipex-llm
非常好用的大语言模型推理框架 bigdl-llm,现改名为 ipex-llm bigdl-llmgithub地址环境安装依赖下载测试模型加载和优化预训练模型使用优化后的模型构建一个聊天应用 bigdl-llm IPEX-LLM is a PyTorch library for running LLM on Intel CPU and GPU (e.g., local P…...

Kubernetes示例yaml:3. service-statefulset.yaml
service-statefulset.yaml 示例 apiVersion: apps/v1 kind: statefulset metadata:...... spec:......volumeMounts:- name: pvcmountPath: /var/lib/arangodb3VolumeClaimTemplates:- metadata:name: pvcspec:accessModes: [ "ReadWriteOnce" ]storangeClassName: …...

Windows平台cmake编译QT源码库,使用VScode开发QT
不愿意安装庞大的QT开发IDE,可以编译QT源码库。 下载源码可以用国内镜像,如清华大学的:Index of /qt/archive/qt/ | 清华大学开源软件镜像站 | Tsinghua Open Source Mirror 我用的是 6.5.3,进去之后,不要下载整个源…...

腾讯云轻量8核16G18M服务器多少钱一年?
腾讯云轻量8核16G18M服务器多少钱一年?优惠价格4224元15个月,买一年送3个月。配置为轻量应用服务器、16核32G28M、28M带宽、6000GB月流量、上海/广州/北京、380GB SSD云硬盘。 腾讯云服务器有两个活动,一个是官方的主会场入口,还…...
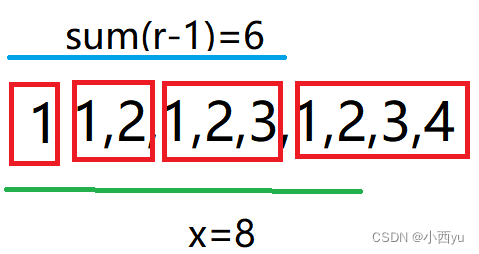
二分练习题——123
123 二分等差数列求和前缀和数组 题目分析 连续一段的和我们想到了前缀和,但是这里的l和r的范围为1e12,明显不能用O(n)的时间复杂度去求前缀和。那么我们开始观察序列的特点,可以按照等差数列对序列进行分块。如上图,在求前10个…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...
