CCF-CSP真题202206-2《寻宝!大冒险!》
题目背景
暑假要到了。可惜由于种种原因,小 P 原本的出游计划取消。失望的小 P 只能留在西西艾弗岛上度过一个略显单调的假期……直到……
某天,小 P 获得了一张神秘的藏宝图。
问题描述
西西艾弗岛上种有 n 棵树,这些树的具体位置记录在一张绿化图上。
简单地说,西西艾弗岛绿化图可以视作一个大小为 (L+1)×(L+1) 的 01 矩阵 A,
地图左下角(坐标 (0,0))和右上角(坐标 (L,L))分别对应 A[0][0] 和 A[L][L]。
其中 A[i][j]=1 表示坐标 (i,j) 处种有一棵树,A[i][j]=0 则表示坐标 (i,j) 处没有树。
换言之,矩阵 A 中有且仅有的 n 个 1 展示了西西艾弗岛上 n 棵树的具体位置。
传说,大冒险家顿顿的宝藏就埋藏在某棵树下。
并且,顿顿还从西西艾弗岛的绿化图上剪下了一小块,制作成藏宝图指示其位置。
具体来说,藏宝图可以看作一个大小为 (S+1)×(S+1) 的 01 矩阵 B(S 远小于 L),对应着 A 中的某一部分。
理论上,绿化图 A 中存在着一处坐标 (x,y)(0≤x,y≤L−S)与藏宝图 B 左下角 (0,0) 相对应,即满足:
对 B 上任意一处坐标 (i,j)(0≤i,j≤S),都有 A[x+i][y+j]=B[i][j]。
当上述条件满足时,我们就认为藏宝图 B 对应着绿化图 A 中左下角为 (x,y)、右上角为 (x+i,y+j) 的区域。
实际上,考虑到藏宝图仅描绘了很小的一个范围,满足上述条件的坐标 (x,y) 很可能存在多个。
请结合西西艾弗岛绿化图中 n 棵树的位置,以及小 P 手中的藏宝图,判断绿化图中有多少处坐标满足条件。
特别地,藏宝图左下角位置一定是一棵树,即 A[x][y]=B[0][0]=1,表示了宝藏埋藏的位置。
输入格式
从标准输入读入数据。
输入的第一行包含空格分隔的三个正整数 n、L 和 S,分别表示西西艾弗岛上树的棵数、绿化图和藏宝图的大小。
由于绿化图尺寸过大,输入数据中仅包含 n 棵树的坐标而非完整的地图;即接下来 n 行每行包含空格分隔的两个整数 x 和 y,表示一棵树的坐标,满足 0≤x,y≤L 且同一坐标不会重复出现。
最后 (S+1) 行输入小 P 手中完整的藏宝图,其中第 i 行(0≤i≤S)包含空格分隔的 (S+1) 个 0 和 1,表示 B[S−i][0]⋯B[S−i][S]。
需要注意,最先输入的是 B[S][0]⋯B[S][S] 一行,B[0][0]⋯B[0][S] 一行最后输入。
输出格式
输出到标准输出。
输出一个整数,表示绿化图中有多少处坐标可以与藏宝图左下角对应,即可能埋藏着顿顿的宝藏。
样例 1 输入
5 100 2
0 0
1 1
2 2
3 3
4 4
0 0 1
0 1 0
1 0 0
样例 1 输出
3
样例 1 解释
绿化图上 (0,0)、(1,1) 和 (2,2) 三处均可能埋有宝藏。
样例 2 输入
5 4 2
0 0
1 1
2 2
3 3
4 4
0 0 0
0 1 0
1 0 0
样例 2 输出
0
样例 2 解释
如果将藏宝图左下角与绿化图 (3,3) 处对应,则藏宝图右上角会超出绿化图边界,对应不成功。
子任务
40% 的测试数据满足:L≤50;
70% 的测试数据满足:L≤2000;
全部的测试数据满足:n≤1000、L≤ 且 S≤50。
提示
实际测试数据中不包括答案为 0 的用例。
思路:
1、查看测试数据可知遍历绿化图肯定会超时,因为最大可达10的9次方,观察题目发现藏宝图左下角位置一定是一棵树,即 A[x][y]=B[0][0]=1,表示了宝藏埋藏的位置,而绿化图中树的个数最多只有1000棵,可在满足藏宝图左下角的而情况下遍历绿化图中的每一棵树来进行判断。
2、若藏宝图中有一个位置的01情况与绿化图中不一致,则直接遍历下一棵树。
代码实现:
#include<iostream>
#include<vector>
#include<map>
#include<algorithm>
using namespace std;int main() {int n, L, S;cin >> n >> L >> S;map<pair<int,int>, int>Tree;vector<vector<int>>Graph;for (int i = 0; i < n; ++i) { //利用一个有序哈希表来存储绿化图中哪些点有坐标int x, y; cin >> x >> y;++Tree[{x,y}]; //其中哈希表的key为两个坐标,value++使其等于1表示该点有树}for (int i = 0; i <= S; ++i) { //藏宝图坐标的输入vector<int>tmp;for (int j = 0; j <= S; ++j) {int x;cin >> x;tmp.push_back(x);}Graph.push_back(tmp); }reverse(Graph.begin(), Graph.end()); //题目说明藏宝图的最后一次输入是第一行,所以进行一次反转int res = 0;//测试数据L最大可达10的9次方,遍历绿化图显然不切合实际,题目说明藏宝图左下角位置一定是一棵树,//即Graph[0][0]=1,表示了宝藏埋藏的位置,因此以绿化图的每一棵树作为藏宝图左下角为起点,遍历藏宝图来进行判断,因为藏宝图的大小S最大也为50for (auto& s : Tree) { //表示以绿化图的每一棵树坐标开始 if (s.first.first + S > L || s.first.second + S > L) //绿化图起始坐标加上藏宝图大小越界绿化图则直接continuecontinue;else {int i, j;bool flag = true; //此标志位是为了跳出两层循环for (i = 0; i <= S; ++i) { //i是藏宝图横坐标for (j = 0; j <= S; ++j) { //j是藏宝图纵坐标//遍历到的坐标藏宝图和绿化图表示的不一样则直接break,表示以绿化图这棵树为开始不符合要求,需要判断其他树//s.first.first表示绿化图中树的横坐标,s.first.second表示绿化图中树的纵坐标if (Graph[i][j] != Tree[{s.first.first + i, s.first.second + j}]) {flag = false;break;}}if (!flag) //跳出两层循环遍历其他树break;}if (i > S) //i越界则j一定越界,表示以绿化图这棵树为起点满足要求,结果++++res;}}cout << res << endl;
}相关文章:
CCF-CSP真题202206-2《寻宝!大冒险!》
题目背景 暑假要到了。可惜由于种种原因,小 P 原本的出游计划取消。失望的小 P 只能留在西西艾弗岛上度过一个略显单调的假期……直到…… 某天,小 P 获得了一张神秘的藏宝图。 问题描述 西西艾弗岛上种有 n 棵树,这些树的具体位置记录在…...
Rust编程(三)生命周期与异常处理
生命周期 生命周期,简而言之就是引用的有效作用域。在大多数时候,我们无需手动的声明生命周期,因为编译器可以自动进行推导。生命周期的主要作用是避免悬垂引用,它会导致程序引用了本不该引用的数据: {let r;{let x …...
【办公类-21-11】 20240327三级育婴师 多个二级文件夹的docx合并成docx有页码,转PDF
背景展示:有页码的操作题 背景需求: 实操课终于全部结束了,把考试内容(docx)都写好了 【办公类-21-10】三级育婴师 视频转文字docx(等线小五单倍行距),批量改成“宋体小四、1.5倍行…...
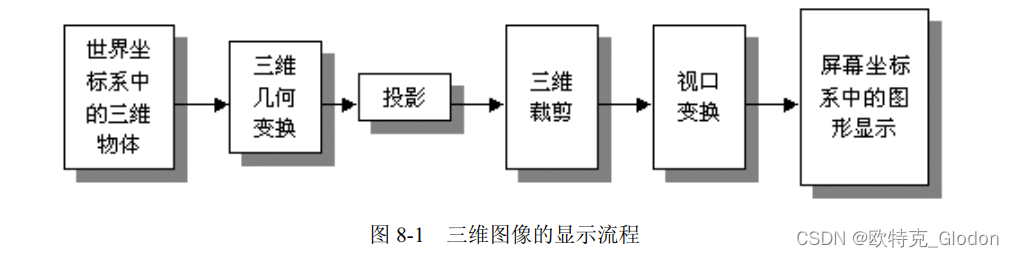
OSG编程指南<二十一>:OSG视图与相机视点更新设置及OSG宽屏变形
1、概述 什么是视图?在《OpenGL 编程指南》中有下面的比喻,从笔者开始学习图形学就影响深刻,相信对读者学习场景管理也会非常有帮助。 产生目标场景视图的变换过程类似于用相机进行拍照,主要有如下的步骤: (1)把照相机固定在三脚架上,让它对准场景(视图变换)。 (2)…...

Laplace变换-3
回忆#常见函数的Laplace变换: t z − 1 ↦ Γ ( z ) s z t^{z-1} \mapsto \frac{\Gamma(z)}{s^{z}} tz−1↦szΓ(z) (要求 R e ( z ) > 0 \mathrm{Re}(z)>0 Re(z)>0) e a t ↦ 1 s − a e^{at} \mapsto \frac{1}{s-a} eat↦s−a1…...
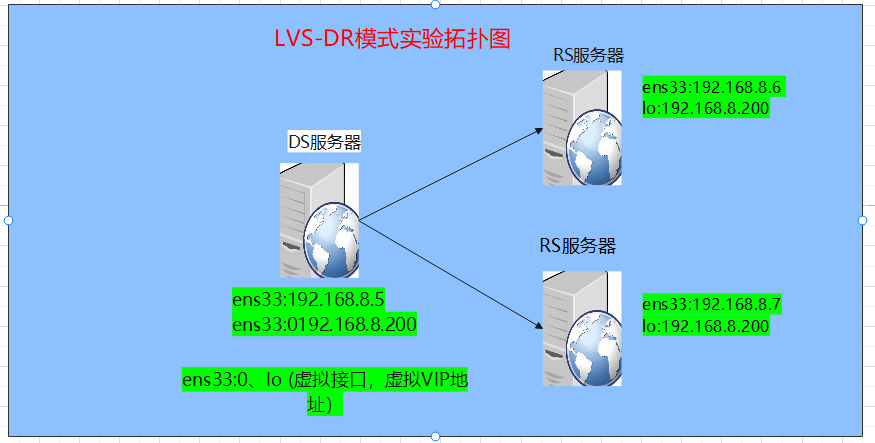
LVS负载均衡-DR模式配置
LVS:Linux virtual server ,即Linux虚拟服务器 LVS自身是一个负载均衡器(Director),不直接处理请求,而是将请求转发至位于它后端的真实服务器real server上。 LVS是四层(传输层 tcp/udp)负载均衡…...
【unity】如何汉化unity Hub
相信大家下载安装unity后看着满操作栏的英文,英文不好的小伙伴们会一头雾水。但是没关系你要记住你要怎么高速运转的机器进入中国,请记住我给出的原理,不懂不代表不会用啊。现在我们就来把编译器给进行汉化。 第一步:我们打开Uni…...

【算法】KMP-快速文本匹配
文章目录 一、KMP算法说明二、详细实现1. next数组定义2. 使用next加速匹配3. next数组如何快速生成4. 时间复杂度O(mn)的证明a) next生成的时间复杂度b) 匹配过程时间复杂度 三、例题1. [leetcode#572](https://leetcode.cn/problems/subtree-of-another-tree/description/)2.…...

多维数组和交错数组笔记
1.) 关于数据的几个概念: Rank,即数组的维数,其值是数组类型的方括号之间逗号个数加上1。 Demo:利用一维数组显示斐波那契数列F(n) F(n-1) F(n-2) (n >2 ),每行显示5项,20项. static void Main(string[] args){int[] F n…...

Python(django)之单一接口展示功能前端开发
1、代码 建立apis_manage.html 代码如下: <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><title>测试平台</title> </head> <body role"document"> <nav c…...

【大模型】非常好用的大语言模型推理框架 bigdl-llm,现改名为 ipex-llm
非常好用的大语言模型推理框架 bigdl-llm,现改名为 ipex-llm bigdl-llmgithub地址环境安装依赖下载测试模型加载和优化预训练模型使用优化后的模型构建一个聊天应用 bigdl-llm IPEX-LLM is a PyTorch library for running LLM on Intel CPU and GPU (e.g., local P…...

Kubernetes示例yaml:3. service-statefulset.yaml
service-statefulset.yaml 示例 apiVersion: apps/v1 kind: statefulset metadata:...... spec:......volumeMounts:- name: pvcmountPath: /var/lib/arangodb3VolumeClaimTemplates:- metadata:name: pvcspec:accessModes: [ "ReadWriteOnce" ]storangeClassName: …...

Windows平台cmake编译QT源码库,使用VScode开发QT
不愿意安装庞大的QT开发IDE,可以编译QT源码库。 下载源码可以用国内镜像,如清华大学的:Index of /qt/archive/qt/ | 清华大学开源软件镜像站 | Tsinghua Open Source Mirror 我用的是 6.5.3,进去之后,不要下载整个源…...

腾讯云轻量8核16G18M服务器多少钱一年?
腾讯云轻量8核16G18M服务器多少钱一年?优惠价格4224元15个月,买一年送3个月。配置为轻量应用服务器、16核32G28M、28M带宽、6000GB月流量、上海/广州/北京、380GB SSD云硬盘。 腾讯云服务器有两个活动,一个是官方的主会场入口,还…...
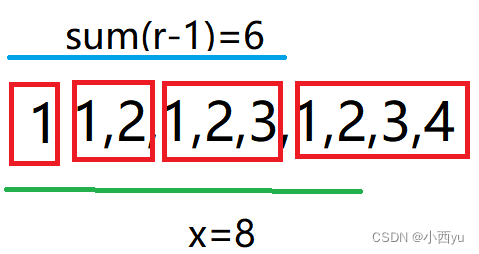
二分练习题——123
123 二分等差数列求和前缀和数组 题目分析 连续一段的和我们想到了前缀和,但是这里的l和r的范围为1e12,明显不能用O(n)的时间复杂度去求前缀和。那么我们开始观察序列的特点,可以按照等差数列对序列进行分块。如上图,在求前10个…...
淘宝详情数据采集(商品上货,数据分析,属性详情,价格监控),海量数据值得get
淘宝详情数据采集涉及多个环节,包括商品上货、数据分析、属性详情以及价格监控等。在采集这些数据时,尤其是面对海量数据时,需要采取有效的方法和技术来确保数据的准确性和完整性。以下是一些关于淘宝详情数据采集的建议: 请求示…...
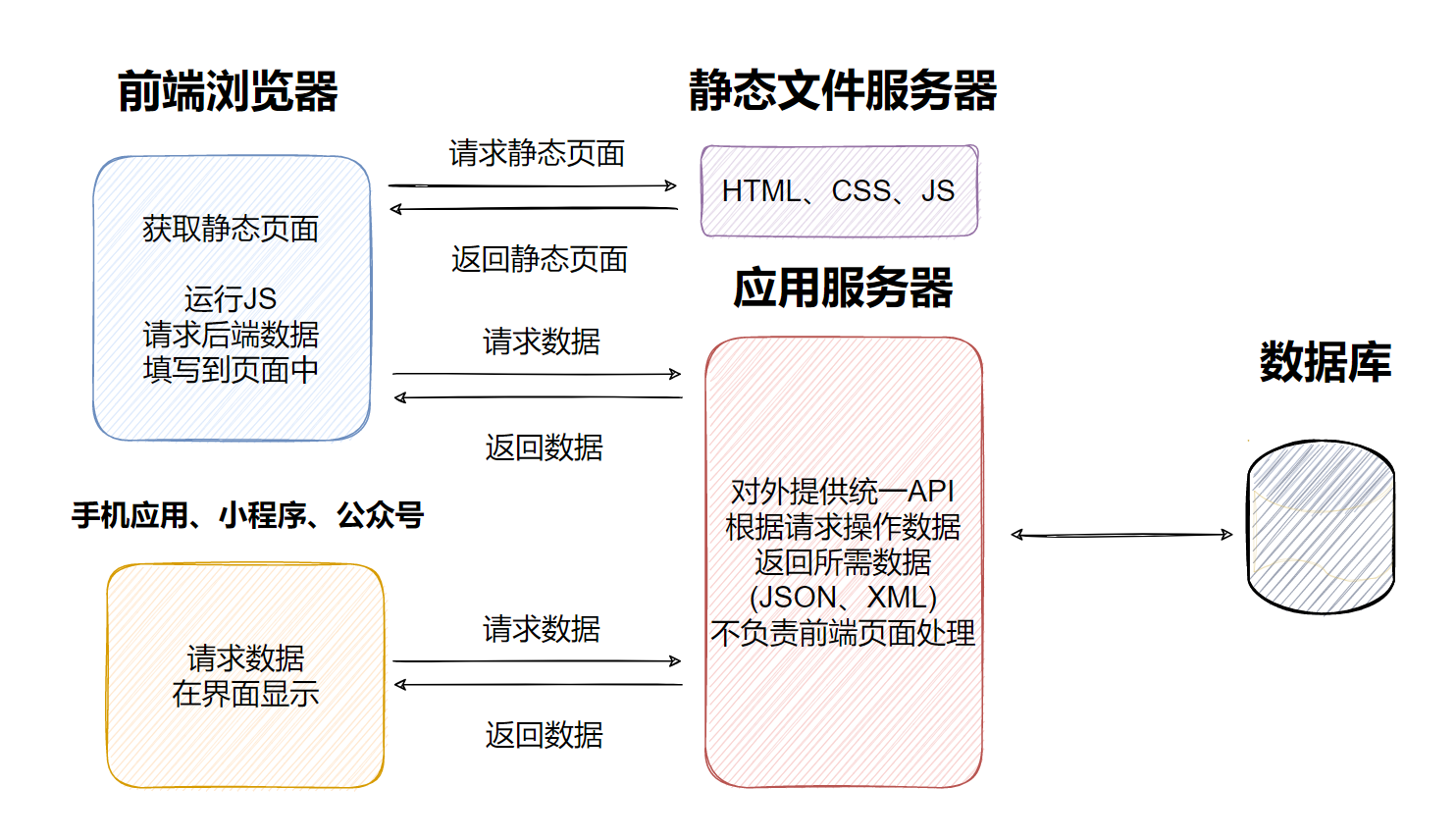
Django之Web应用架构模式
一、Web应用架构模式 在开发Web应用中,有两种模式 1.1、前后端不分离 在前后端不分离的应用模式中,前端页面看到的效果都是由后端控制,由后端渲染页面或重定向,也就是后端需要控制前端的展示。前端与后端的耦合度很高 1.2、前后端分离 在前后端分离的应用模式中,后端仅返…...

GPT提示词分享 —— 口播脚本
可用于撰写视频、直播、播客、分镜头和其他口语内容的脚本。 提示词👇 请以人的口吻,采用缩略语、成语、过渡短语、感叹词、悬垂修饰语和口语化语言,避免重复短语和不自然的句子结构,撰写一篇关于 [主题] 的文章。 GPT3.5&#…...
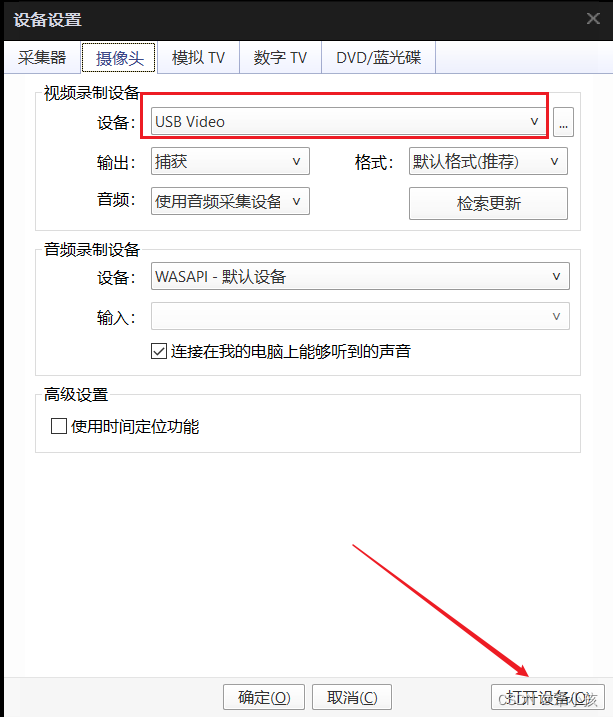
笔记本作为其他主机显示屏(HDMI采集器)
前言: 我打算打笔记本作为显示屏来用,连上工控机,这不是贼方便吗 操作: 一、必需品 HDMI采集器一个 可以去绿联买一个,便宜的就行,我的大概就长这样 win10下载 PotPlayer 软件 下载链接:h…...
02.percona Toolkit工具pt-archiver命令实践
1.命令作用 Percona Toolkit有的32个命令,可以分为7大类 工具类别 工具命令 工具作用 备注 开发类 pt-duplicate-key-checker 列出并删除重复的索引和外键 pt-online-schema-change 在线修改表结构 pt-query-advisor 分析查询语句,并给出建议&#x…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...
