win11 环境配置 之 Jmeter
一、安装 JDK
1. 安装 jdk
截至当前最新时间: 2024.3.27
jdk最新的版本 是
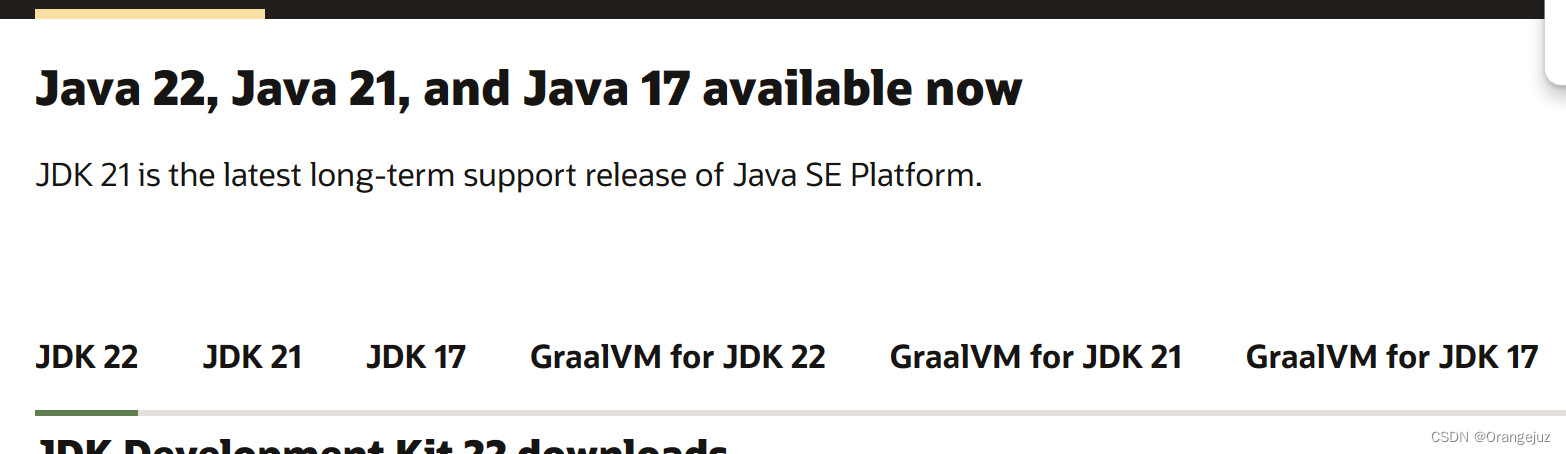
官网下载地址:
https://www.oracle.com/java/technologies/downloads/
建议下载 jdk17
- 另存为到该电脑的 D 盘下,新建jdk文件夹
- 开始安装到 jdk 文件夹下
2. 配置 jdk 环境变量
- 点击搜索环境变量,点击“编辑系统环境变量”即可。

- 配置以下环境变量:
(1)变量名:JAVA_HOME变量值:D:\software\JDK\jdk
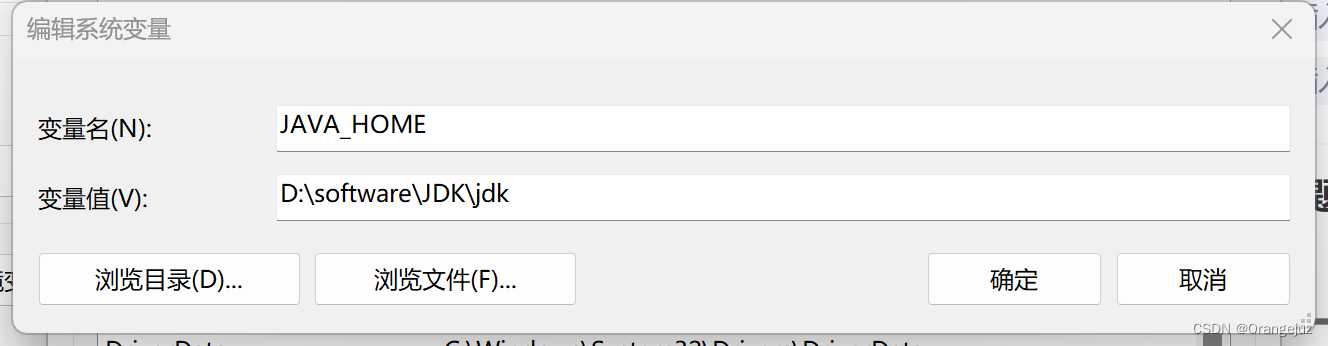
(2)变量名:CLASSPATH 变量值:.;%JAVA_HOME%\lib\dt.jar;%JAVA_HOME%\lib\tools.jar(前面有 . 别掉了)
变量名:path,变量值:%JAVA_HOME%\bin
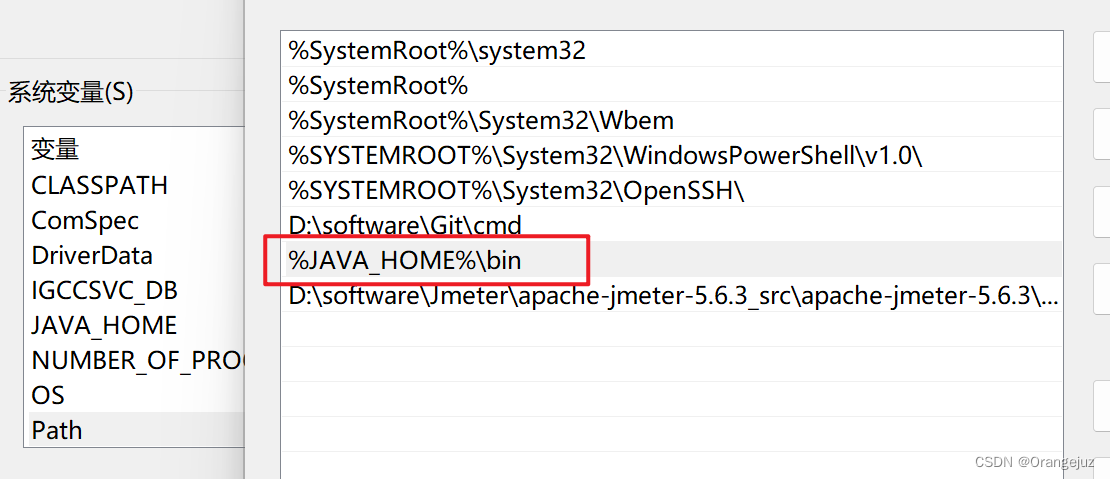
重要注意事项!!
需要删除 path 变量下,一开始就存在的变量值:C:\Program Files\Common Files\Oracle\Java\javapath
3. 查看 jdk17 是否安装成功
- 快捷键 win+R,输入 cmd,点击进入 cmd
- 输入 java -version、java、javac,查看是否有输出,检测是否安装成功
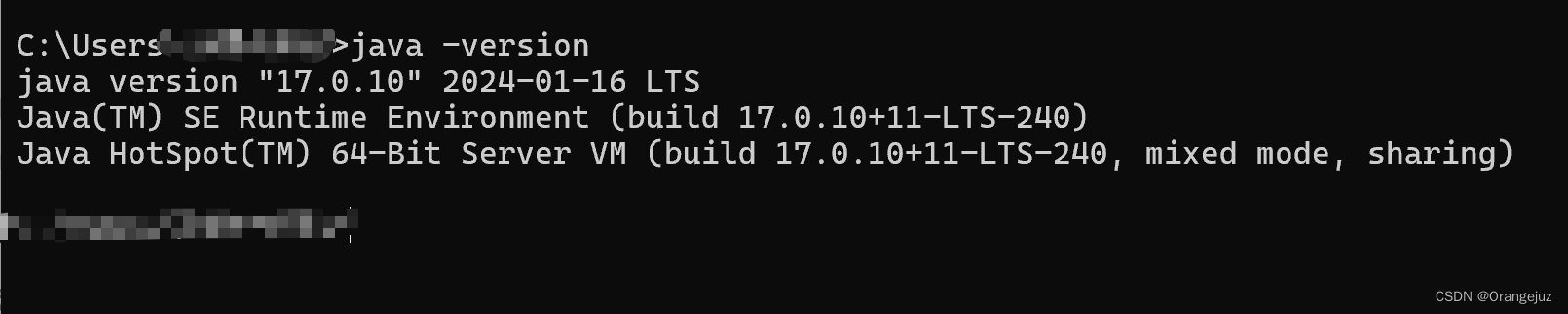
二、安装 jmeter
1. 下载 jemter
官网路径: https://jmeter.apache.org/download_jmeter.cgi
- Binaries - zip 文件(这里我一开始下载错了!!!导致无法成功使用 jmeter)
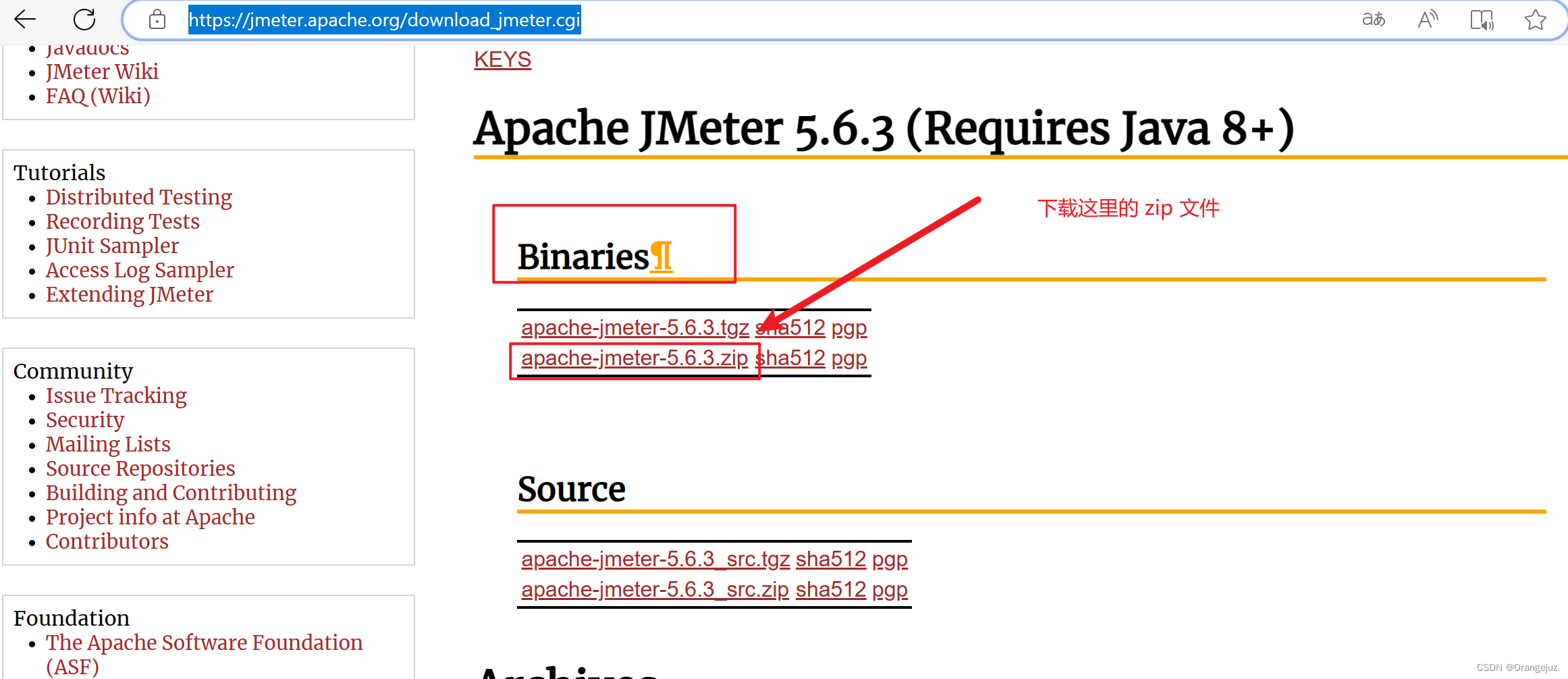
- 下载安装到 本地 D盘路径下
2. 配置 jmeter 环境变量
同 jdk 中,这里只需要配置 变量名:path ,添加一个变量值:D:\software\Jmeter\apache-jmeter-5.6.3_src\apache-jmeter-5.6.3\bin(注意i到bin 目录下)
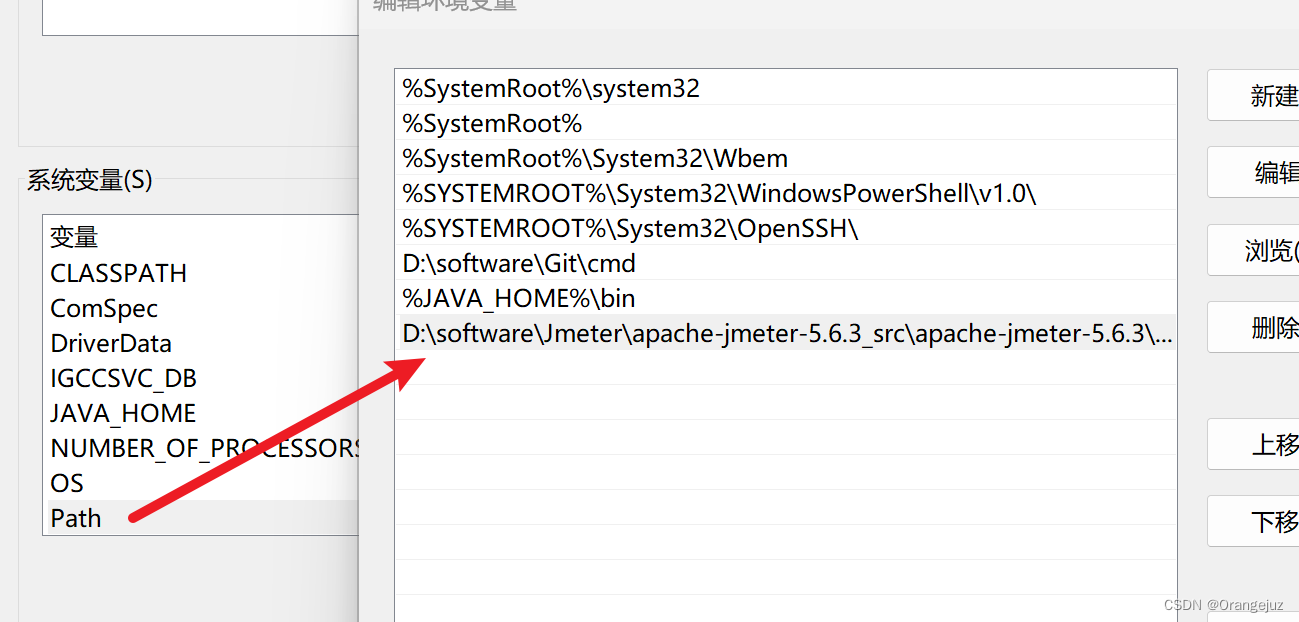
3. 查看 jmeter 是否安装成功
进入 jmeter 文件夹下的bin,双击 jmeter.bat 文件

至此大功告成啦!!!!恭喜你!!!
相关文章:

win11 环境配置 之 Jmeter
一、安装 JDK 1. 安装 jdk 截至当前最新时间: 2024.3.27 jdk最新的版本 是 官网下载地址: https://www.oracle.com/java/technologies/downloads/ 建议下载 jdk17 另存为到该电脑的 D 盘下,新建jdk文件夹 开始安装到 jdk 文件夹下 2. 配…...
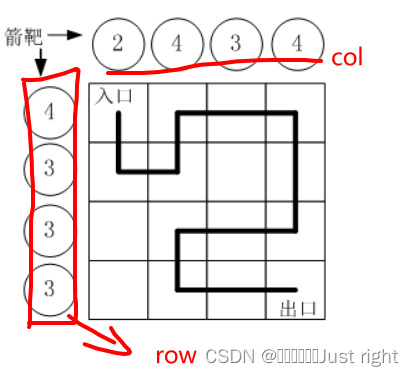
蓝桥杯刷题之路径之谜
题目来源 路径之谜 不愧是国赛的题目 题意 题目中会给你两个数组,我这里是分别用row和col来表示 每走一步,往左边和上边射一箭,走到终点的时候row数组和col数组中的值必须全部等于0这个注意哈,看题目看了半天,因为…...

【深度学习】图片预处理,分辨出模糊图片
ref:https://pyimagesearch.com/2015/09/07/blur-detection-with-opencv/ 论文 ref:https://www.cse.cuhk.edu.hk/leojia/all_final_papers/blur_detect_cvpr08.pdf 遇到模糊的图片,还要处理一下,把它挑出来,要么修复,要么弃用。否…...

基础NLP知识了解
基础NLP知识… 线性变换 通过一个线性变换将隐藏状态映射到另一个维度空间,以获得预期维度的向量 $ outputs hidden_layer * W b$ 这里的W是权重矩阵,b是偏置项,它们是线性变换的参数,通过训练数据学习得到。输出向量的维度…...
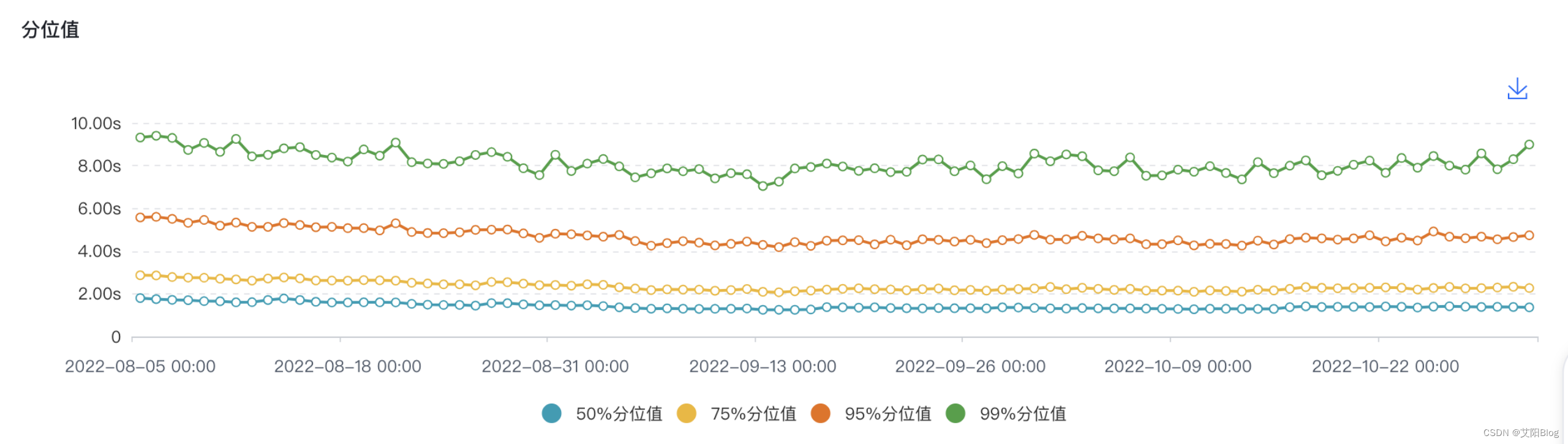
Android 性能优化(六):启动优化的详细流程
书接上文,Android 性能优化(一):闪退、卡顿、耗电、APK 从用户体验角度有四个性能优化方向: 追求稳定,防止崩溃追求流畅,防止卡顿追求续航,防止耗损追求精简,防止臃肿 …...
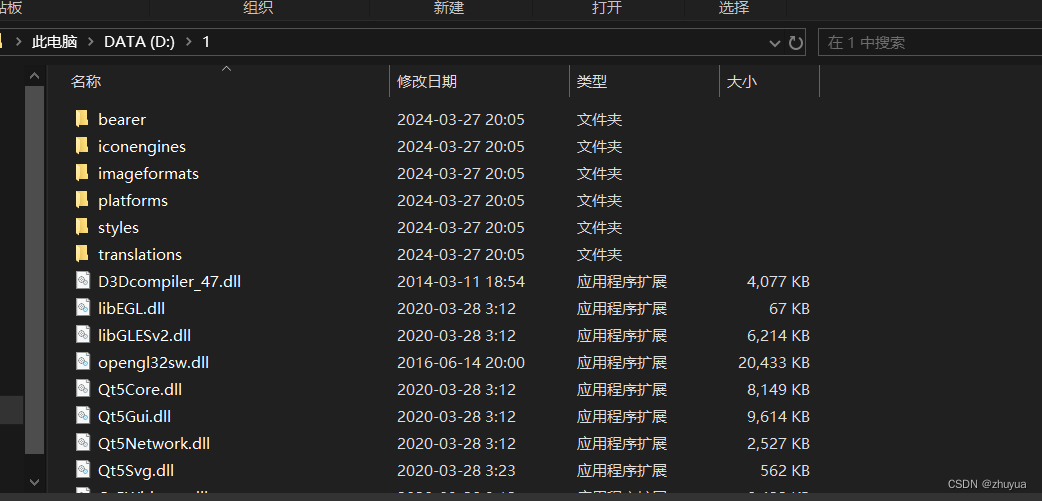
QT程序打包
将exe文件单独拿出来放入一个单独的文件夹 保存qt安装路径下有如下这个文件 windeployqt.exe 在TCPFile.exe文件夹中使用以下cmd命令运行 即可打包 windeployqt 文件名.exe 成功打包!...
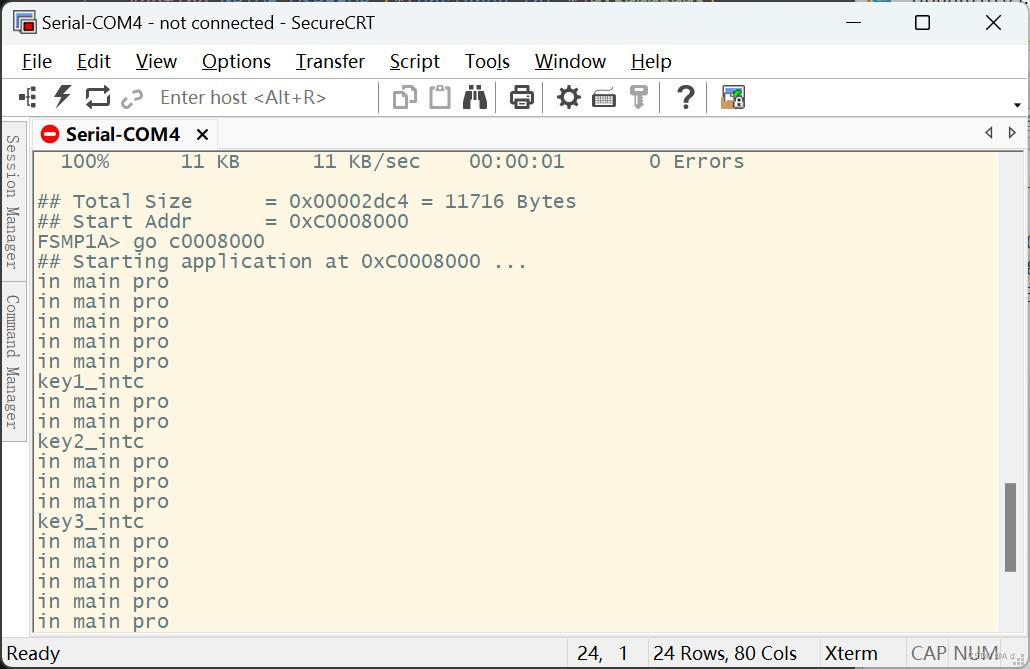
ARMday7作业
实现三个按键的中断,现象和代码 do_ipr.c #include "stm32mp1xx_gic.h" #include "stm32mp1xx_exti.h" extern void printf(const char *fmt, ...); unsigned int i 0; void do_irq(void) {//获取要处理的中断的中断号unsigned int irqnoGI…...
——SBP的依赖后处理)
Unity构建详解(4)——SBP的依赖后处理
【AddHashToBundleNameTask】 这个Task的作用很明确,给Bundle的名字附加一个Hash值: 根据bundle所包含的asset计算出来一个hash值添加在原来Bundle的末尾替换了BundleBuildContent.BundleLayout和aa.bundleToAssetGroup中的key 有两个问题,…...

使用GO对PostgreSQL进行有意思的多线程压测
前言 针对PostgreSQL进行压缩,有很多相关的工具。有同学又要问了,为何还要再搞一个?比如,pgbench, sysbench之类的,已经很强大了。是的,它们都很强大。但有时候,在一些特殊的场景,可…...
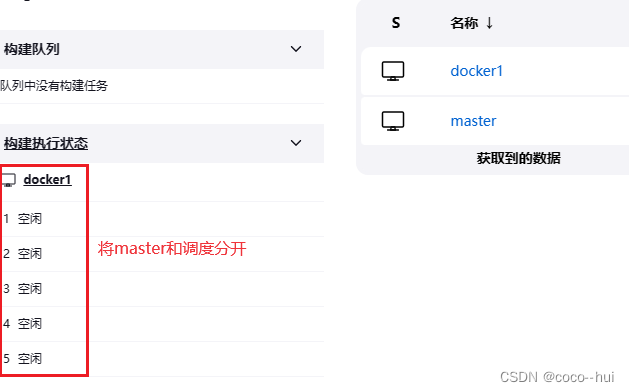
CI/CI实战-jenkis结合gitlab 4
实时触发 安装gitlab插件 配置项目触发器 生成令牌并保存 配置gitlab 测试推送 gitlab的实时触发 添加jenkins节点 在jenkins节点上安装docker-ce 新建节点server3 安装git和jdx 在jenkins配置管理中添加节点并配置从节点 关闭master节点的构建任务数...
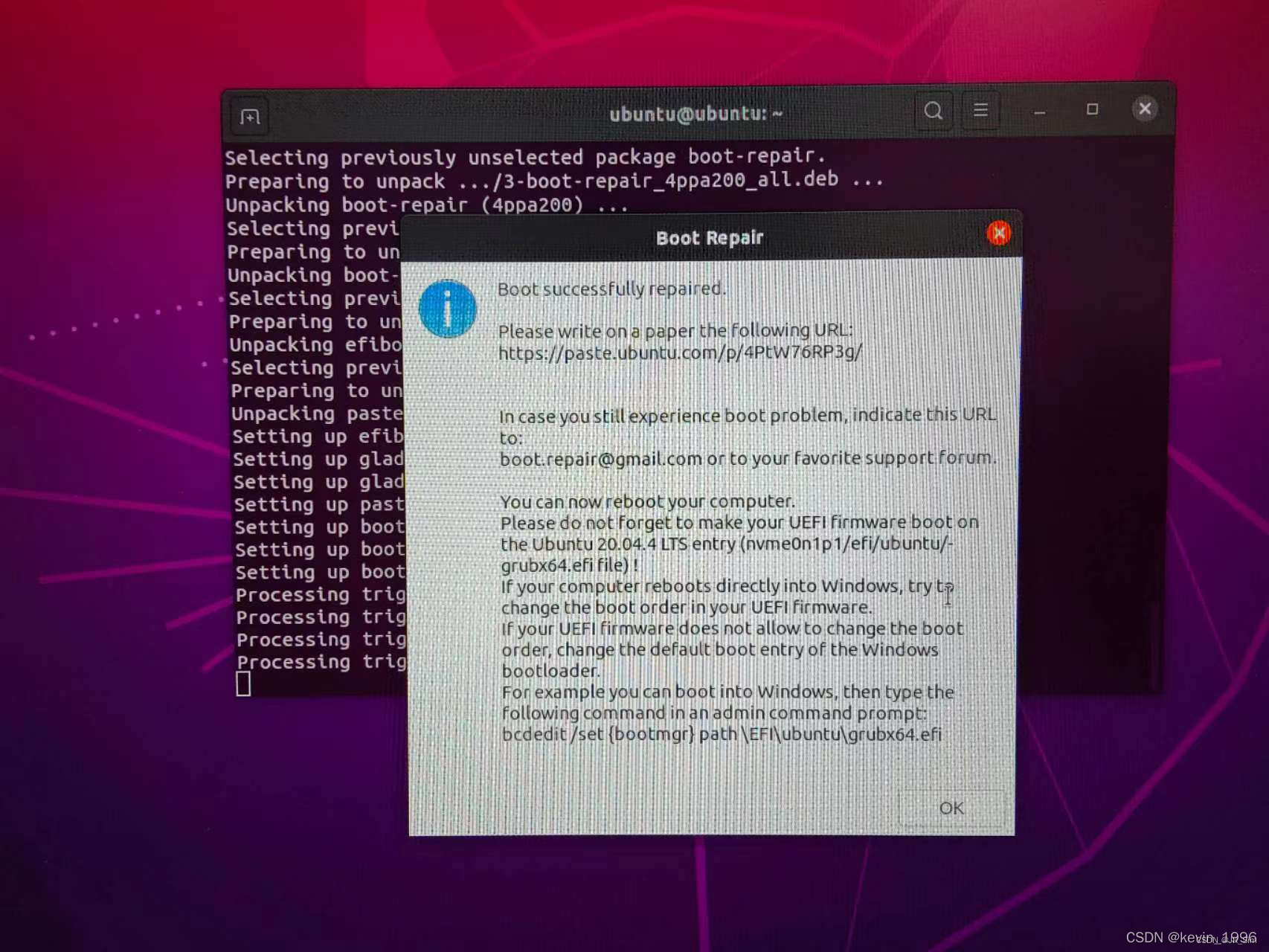
修复ubuntu引导
一、制作ubuntu启动U盘 进入启动盘后,点击Try ubuntu,进入U盘的ubuntu系统。 二、配置和添加源 sudo add-apt-repository ppa:yannubuntu/boot-repair && sudo apt-get update三、运行 Boot Repair重新制作引导 sudo boot-repair注意&#x…...
11.Notepad++
文章目录 一、下载和安装设置练习 以前在记事本上写的代码看上去有点累,因为所有的单词看上去都是黑色的,并且当代码出现问题后,它提示第三行,我们还需要一行一行去数。这些问题都可以由一个高级记事本: Notepad 来解…...

实现阻塞队列
import java.util.concurrent.ArrayBlockingQueue; import java.util.concurrent.BlockingQueue; import java.util.concurrent.LinkedBlockingQueue; public class Main { public static void main(String[] args) throws InterruptedException { BlockingQue…...

MySQL8.X驱动datetime映射问题
MySQL8.X驱动datetime映射问题 背景:项目由SSM项目迁移至SpringBoot,对mysql数据库驱动进行了升级导致出现问题。 原因:mysql驱动的8.X版本对数据库类型datetime映射为LocalDateTime。 解决:暂时不升级mysql驱动,mys…...
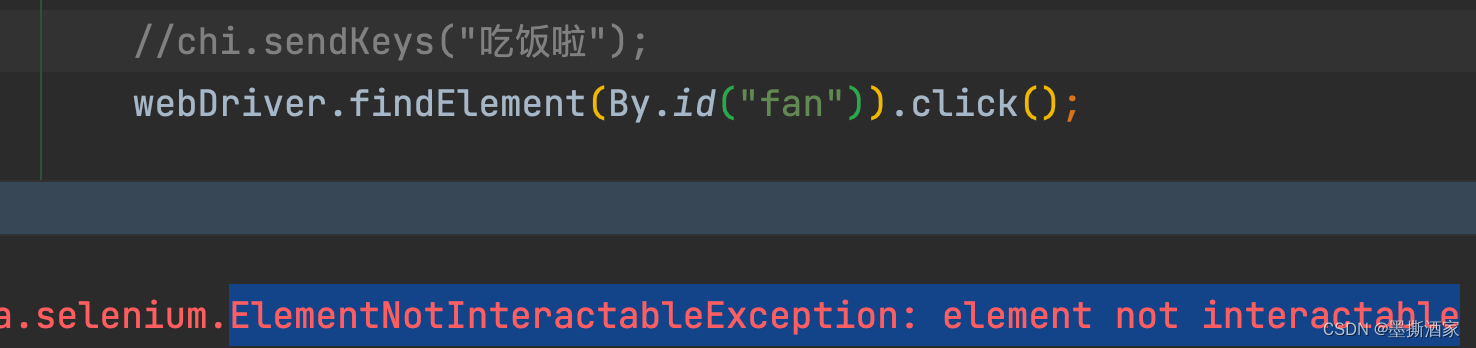
【Selenium】隐藏元素的定位和操作|隐藏与isDisplay方法
一、selenium 中隐藏元素如何定位? 如果单纯的定位的话,隐藏元素和普通不隐藏元素定位没啥区别,用正常定位方法就行了 但是吧~~~能定位到并不意味着能操作元素(如click,clear,send_keys) 二、隐藏元素 如下图有个输入框…...

视图的作用
目录 视图的作用 创建视图 为 scott 分配创建视图的权限 查询视图 复杂视图的创建 视图更新的限制问题 更新视图中数据的部门编号(视图的存在条件) 限制通过视图修改数据表内容 创建只读的视图 复杂视图创建 oracle从入门到总裁:h…...

动态ip白名单频繁更改问题解决方案
1. 使用静态IP地址:可以通过向ISP申请静态IP地址来解决动态IP地址的变化问题,但是这种方法会比较贵。 2. 使用动态DNS:可以使用动态DNS服务,它可以将动态IP地址映射到一个固定的域名,从而使得动态IP地址处理为域名一直…...

什么是物联网监控平台?部署物联网平台有什么作用?
随着物联网技术的飞速发展,越来越多的企业开始关注并投入到这一领域。物联网监控平台作为连接物理世界与数字世界的桥梁,正逐渐成为企业数字化转型的关键组件。今天,我们将深入探讨物联网监控平台的定义、部署物联网平台的作用,以…...
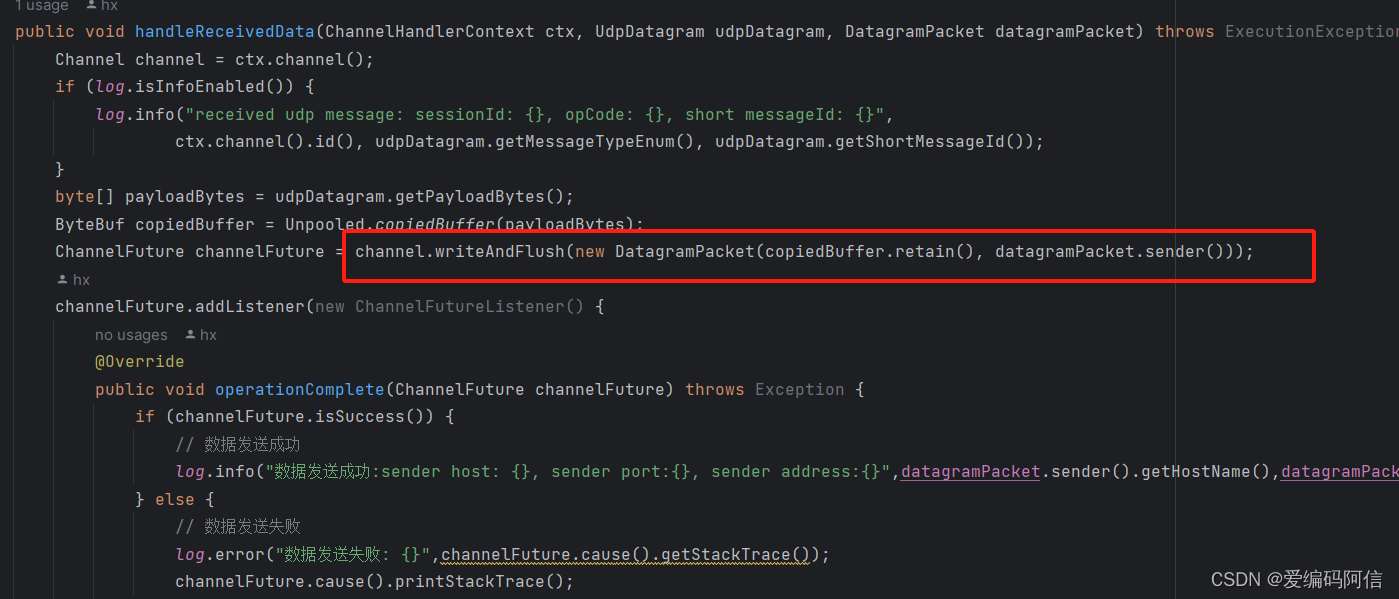
netty构建udp服务器以及发送报文到客户端客户端详细案例
目录 一、基于netty创建udp服务端以及对应通道设置关键 二、发送数据 三、netty中的ChannelOption常用参数说明 1、ChannelOption.SO_BACKLOG 2、ChannelOption.SO_REUSEADDR 3、ChannelOption.SO_KEEPALIVE 4、ChannelOption.SO_SNDBUF和ChannelOption.SO_RCVBUF 5、Ch…...
——软件测试之小结)
Selenium 学习(0.22)——软件测试之小结
Junit 等一系列自动化工具不用啰嗦了,自己就是小白再搞科普就装了。 把后面相关内容看了一下,使用这些测试工具一样编写代码(驱动模块【调用接口的代码片段】,桩模块【响应输出结果的代码片段,也就是被测模块调用的模块…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...
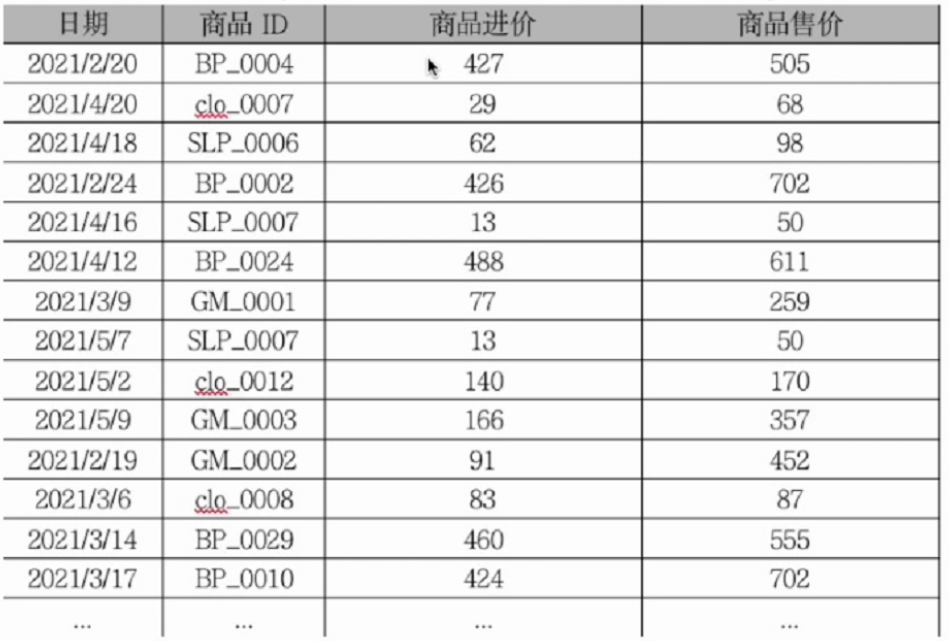
智警杯备赛--excel模块
数据透视与图表制作 创建步骤 创建 1.在Excel的插入或者数据标签页下找到数据透视表的按钮 2.将数据放进“请选择单元格区域“中,点击确定 这是最终结果,但是由于环境启不了,这里用的是自己的excel,真实的环境中的excel根据实训…...
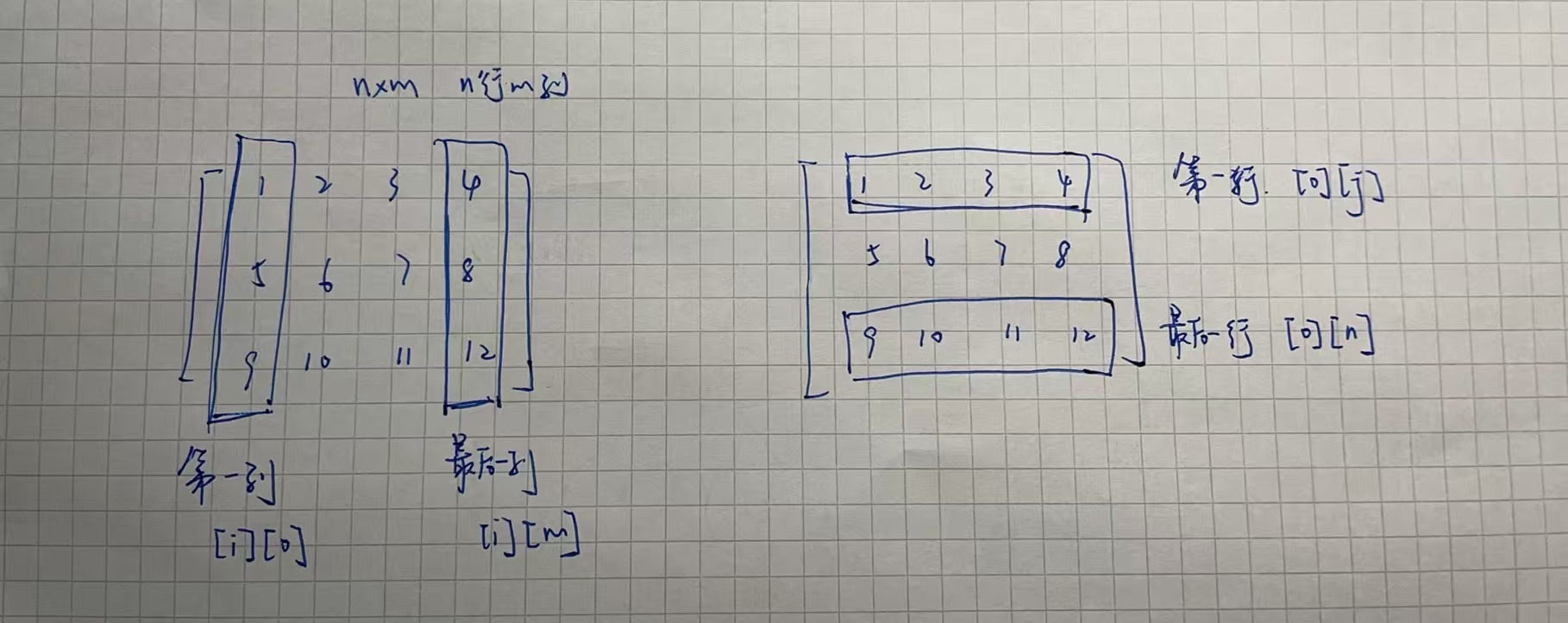
二维数组 行列混淆区分 js
二维数组定义 行 row:是“横着的一整行” 列 column:是“竖着的一整列” 在 JavaScript 里访问二维数组 grid[i][j] 表示 第i行第j列的元素 let grid [[1, 2, 3], // 第0行[4, 5, 6], // 第1行[7, 8, 9] // 第2行 ];// grid[i][j] 表示 第i行第j列的…...