曲线生成 | 图解Reeds-Shepp曲线生成原理(附ROS C++/Python/Matlab仿真)
目录
- 0 专栏介绍
- 1 什么是Reeds-Shepp曲线?
- 2 Reeds-Shepp曲线的运动模式
- 3 Reeds-Shepp曲线算法原理
- 3.1 坐标变换
- 3.2 时间翻转(time-flip)
- 3.3 反射变换(reflect)
- 3.4 后向变换(backwards)
- 4 仿真实现
- 4.1 ROS C++实现
- 4.2 Python实现
- 4.3 Matlab实现
0 专栏介绍
🔥附C++/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备!详细介绍全局规划(图搜索、采样法、智能算法等);局部规划(DWA、APF等);曲线优化(贝塞尔曲线、B样条曲线等)。
🚀详情:图解自动驾驶中的运动规划(Motion Planning),附几十种规划算法
1 什么是Reeds-Shepp曲线?
Reeds-Shepp曲线是一种用于描述在平面上从一个点到另一个点最优路径的数学模型。这种曲线是由美国数学家 J. A. Reeds 和 L. A. Shepp 在1990年提出的,它被广泛应用于路径规划和运动规划问题中。Reeds-Shepp曲线的很多原理和Dubins曲线类似,可以先学习曲线生成 | 图解Dubins曲线生成原理(附ROS C++/Python/Matlab仿真)

Reeds-Shepp曲线具有以下特点:
- 最优性:Reeds-Shepp曲线是连接两个点的最短路径之一,通常是沿着曲线长度最短的路径。相比于Dubins曲线只允许车辆向前运动,RS曲线同时允许车辆前向、后向运动,使得在某些情况下可以得出比 Dubins 曲线更优的解
- 约束性:曲线遵循机器人或车辆的运动学约束,例如最大转角、最大速度等。
- 多样性:存在不同类型的Reeds-Shepp曲线,例如直线-圆弧-直线(L-S-L)、直线-圆弧-反向圆弧-直线(L-S-R-S)等,以适应不同场景下的路径规划需求。
通过计算和生成Reeds-Shepp曲线,可以帮助机器人或车辆高效地规划路径并完成复杂的运动任务。
2 Reeds-Shepp曲线的运动模式
经过证明,RS曲线从起点到终点的最短路径一定是下面的组合之一
{ C ∣ C ∣ C , C C ∣ C , C ∣ C C , C S C , C C β ∣ C β C , C ∣ C β C β ∣ C , C ∣ C π / 2 S C , C S C π / 2 ∣ C , C ∣ C π / 2 S C π / 2 ∣ C } \left\{ \begin{array}{c} C|C|C, CC|C, C|CC, CSC, CC_{\beta}|C_{\beta}C, C|C_{\beta}C_{\beta}|C,\\ C|C_{{{\pi}/{2}}}SC, CSC_{{{\pi}/{2}}}|C, C|C_{{{\pi}/{2}}}SC_{{{\pi}/{2}}}|C\\\end{array} \right\} {C∣C∣C,CC∣C,C∣CC,CSC,CCβ∣CβC,C∣CβCβ∣C,C∣Cπ/2SC,CSCπ/2∣C,C∣Cπ/2SCπ/2∣C}
其中 C C C表示圆弧运动, S S S表示直线运动,|表示车辆运动朝向发生改变。带 π / 2 \pi/2 π/2下标表示该段轨迹弧长对应的角度为 π / 2 \pi/2 π/2,带 β \beta β下标表示相邻两段轨迹弧长对应的角度相等。将上述组合完整展开后对应如表所示的48种运动模式,其中+代表前行,-代表倒车。后续经过证明, ( L − R + L − ) \left( L^-R^+L^- \right) (L−R+L−)与 ( R − L + R − ) \left( R^-L^+R^- \right) (R−L+R−)两种序列是多余的。

RS曲线在实现上的复杂度远远高于只有6种组合的Dubins曲线,考虑到序列间的对称关系,引入下面的变换简化曲线求解过程。
3 Reeds-Shepp曲线算法原理
3.1 坐标变换
类似Dubins曲线的思想进行坐标变换。在全局坐标系 x O y xOy xOy中,设机器人起始位姿 p s \boldsymbol{p}_s ps、终止位姿 p g \boldsymbol{p}_g pg、最小转弯半径分别为 ( x s , y s , α ) \left( x_s,y_s,\alpha \right) (xs,ys,α)、 ( x g , y g , β ) \left( x_g,y_g,\beta \right) (xg,yg,β)与 R R R。以 p s \boldsymbol{p}_s ps为新坐标系原点,位姿角 α \alpha α方向为 x ′ x' x′轴,垂直方向为 y ′ y' y′轴建立新坐标系 ,同样考虑归一化最小转弯半径
p s ′ = [ 0 0 0 ] , p g ′ = [ ( x g cos β + y g sin β ) R ( − x g sin β + y g cos β ) R β − α ] \boldsymbol{p}_{s}^{'}=\left[ \begin{array}{c} 0\\ 0\\ 0\\\end{array} \right] , \boldsymbol{p}_{g}^{'}=\left[ \begin{array}{c} \left( x_g\cos \beta +y_g\sin \beta \right) R\\ \left( -x_g\sin \beta +y_g\cos \beta \right) R\\ \beta -\alpha\\\end{array} \right] ps′= 000 ,pg′= (xgcosβ+ygsinβ)R(−xgsinβ+ygcosβ)Rβ−α
3.2 时间翻转(time-flip)
将计算曲线的运动方向全部取反,得到的新曲线与原曲线具有时间翻转关系。如图所示,以 L − R + S + L + ↔ L + R − S − L − L^-R^+S^+L^+\leftrightarrow L^+R^-S^-L^- L−R+S+L+↔L+R−S−L−为例解释时间翻转:设实现了对 L − R + S + L + L^-R^+S^+L^+ L−R+S+L+的计算 f ( x , y , ϕ ) f\left( x,y,\phi \right) f(x,y,ϕ),若用同样的函数计算 f ( − x , y , − ϕ ) f\left( -x,y,-\phi \right) f(−x,y,−ϕ),并将各段路径取反,则等价于以轨迹 L + R − S − L − L^+R^-S^-L^- L+R−S−L−到达 ( x , y , ϕ ) \left( x,y,\phi \right) (x,y,ϕ)。
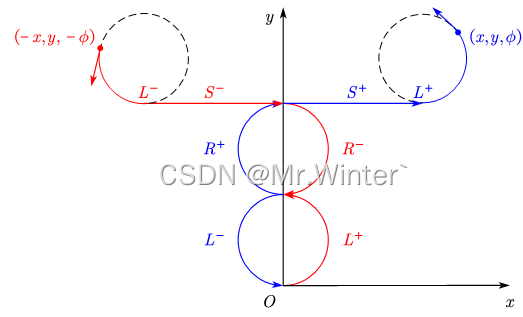
3.3 反射变换(reflect)
将计算曲线的圆周运动类型全部取反,得到的新曲线与原曲线具有反射变换关系。如图所示,以 L − R + S + L + ↔ R − L + S + R + L^-R^+S^+L^+\leftrightarrow R^-L^+S^+R^+ L−R+S+L+↔R−L+S+R+为例解释仿射变换:设实现了对 L − R + S + L + L^-R^+S^+L^+ L−R+S+L+的计算 f ( x , y , ϕ ) f\left( x,y,\phi \right) f(x,y,ϕ),若用同样的函数计算 f ( x , − y , − ϕ ) f\left( x,-y,-\phi \right) f(x,−y,−ϕ),并将圆弧段类型取反,则等价于以轨迹 R − L + S + R + R^-L^+S^+R^+ R−L+S+R+到达 ( x , y , ϕ ) \left( x,y,\phi \right) (x,y,ϕ)。

3.4 后向变换(backwards)
将计算曲线的轨迹段逆序,得到的新曲线与原曲线具有后向变换关系。如图所示,以 L − R + S + L + ↔ L + S + R + L − L^-R^+S^+L^+\leftrightarrow L^+S^+R^+L^- L−R+S+L+↔L+S+R+L−为例解释后向变换:设实现了对 L − R + S + L + L^-R^+S^+L^+ L−R+S+L+的计算 f ( x , y , ϕ ) f\left( x,y,\phi \right) f(x,y,ϕ),若用同样的函数计算 f ( x cos ϕ + y sin ϕ , x sin ϕ − y cos ϕ , ϕ ) f\left( x\cos \phi +y\sin \phi ,x\sin \phi -y\cos \phi ,\phi \right) f(xcosϕ+ysinϕ,xsinϕ−ycosϕ,ϕ),并将计算曲线逆序,则等价于以轨迹 L + S + R + L − L^+S^+R^+L^- L+S+R+L−到达 ( x , y , ϕ ) \left( x,y,\phi \right) (x,y,ϕ)。

4 仿真实现
4.1 ROS C++实现
核心代码如下所示
Points2d ReedsShepp::generation(Pose2d start, Pose2d goal)
{...// coordinate transformation...// select the best motionRSPath best_path({ REEDS_SHEPP_MAX }, { REEDS_SHEPP_NONE });_update(SCS(x, y, dyaw), best_path);_update(CCC(x, y, dyaw), best_path);_update(CSC(x, y, dyaw), best_path);_update(CCCC(x, y, dyaw), best_path);_update(CCSC(x, y, dyaw), best_path);_update(CCSCC(x, y, dyaw), best_path);if (best_path.len() == REEDS_SHEPP_MAX)return path;// interpolationint points_num = int(best_path.len() / step_) + 6;int i = 0;for (size_t j = 0; j < best_path.size(); j++){int m;double seg_length;best_path.get(j, seg_length, m);// path incrementdouble d_l = seg_length > 0.0 ? step_ : -step_;double x = path_x[i];double y = path_y[i];double yaw = path_yaw[i];// current path lengthdouble l = d_l;while (fabs(l) <= fabs(seg_length)){i += 1;std::tie(path_x[i], path_y[i], path_yaw[i]) = interpolate(m, l, { x, y, yaw });l += d_l;}i += 1;std::tie(path_x[i], path_y[i], path_yaw[i]) = interpolate(m, seg_length, { x, y, yaw });}// remove unused data...// coordinate transformation...return path;
}
4.2 Python实现
核心代码如下所示
def generation(self, start_pose: tuple, goal_pose: tuple):sx, sy, syaw = start_posegx, gy, gyaw = goal_pose# coordinate transformation...# select the best motionplanners = [self.SCS, self.CCC, self.CSC, self.CCCC, self.CCSC, self.CCSCC]best_path, best_cost = None, float("inf")for planner in planners:paths = planner(x, y, dyaw)for path in paths:if path.path_length < best_cost:best_path, best_cost = path, path.path_length# interpolationpoints_num = int(best_cost / self.step) + len(best_path.lengths) + 3x_list = [0.0 for _ in range(points_num)]y_list = [0.0 for _ in range(points_num)]yaw_list = [0.0 for _ in range(points_num)]i = 0for mode_, seg_length in zip(best_path.ctypes, best_path.lengths):# path incrementd_length = self.step if seg_length > 0.0 else -self.stepx, y, yaw = x_list[i], y_list[i], yaw_list[i]# current path lengthlength = d_lengthwhile abs(length) <= abs(seg_length):i += 1x_list[i], y_list[i], yaw_list[i] = self.interpolate(mode_, length, (x, y, yaw))length += d_lengthi += 1x_list[i], y_list[i], yaw_list[i] = self.interpolate(mode_, seg_length, (x, y, yaw))# failed...# remove unused data...# coordinate transformation...return best_cost / self.max_curv, best_path.ctypes, x_list_, y_list_, yaw_list_

4.3 Matlab实现
核心代码如下所示
function [x_list, y_list, yaw_list] = generation(start_pose, goal_pose, param) % coordinate transformation...% select the best motionplanners = ["SCS", "CCC", "CSC", "CCCC", "CCSC", "CCSCC"];best_cost = inf;best_path = [];for i=1:length(planners)planner = str2func(planners(i));paths = planner(x, y, dyaw);for j=1:length(paths)if paths(j).len < best_costbest_path = paths(j);best_cost = paths(j).len;endendend% interpolationpoints_num = floor(best_cost / param.step) + length(best_path.segs) + 3;x_list_ = zeros(points_num);y_list_ = zeros(points_num);yaw_list_ = zeros(points_num);i = 1;for j = 1:length(best_path.segs)m = best_path.ctypes(j);seg_length = best_path.segs(j);% path incrementif seg_length > 0.0d_length = param.step;elsed_length = -param.step;endx = x_list_(i); y = y_list_(i); yaw = yaw_list_(i);% current path lengthl = d_length;while abs(l) <= abs(seg_length)i = i + 1;new_pt = interpolate(m, l, [x, y, yaw], param);x_list_(i) = new_pt(1); y_list_(i) = new_pt(2); yaw_list_(i) = new_pt(3);l = l + d_length;endi = i + 1;new_pt = interpolate(m, seg_length, [x, y, yaw], param);x_list_(i) = new_pt(1); y_list_(i) = new_pt(2); yaw_list_(i) = new_pt(3);end% remove unused data...% coordinate transformation...
end

完整工程代码请联系下方博主名片获取
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …
相关文章:

曲线生成 | 图解Reeds-Shepp曲线生成原理(附ROS C++/Python/Matlab仿真)
目录 0 专栏介绍1 什么是Reeds-Shepp曲线?2 Reeds-Shepp曲线的运动模式3 Reeds-Shepp曲线算法原理3.1 坐标变换3.2 时间翻转(time-flip)3.3 反射变换(reflect)3.4 后向变换(backwards) 4 仿真实现4.1 ROS C实现4.2 Python实现4.3 Matlab实现 0 专栏介绍 ǵ…...
深入探讨iOS开发:从创建第一个iOS程序到纯代码实现全面解析
iOS开发作为移动应用开发的重要领域之一,对于开发人员具有重要意义。本文将深入探讨iOS开发的各个方面,从创建第一个iOS程序到纯代码实现iOS开发,带领读者全面了解iOS应用程序的开发流程和技术要点。 📱 第一个iOS程序 在创建第…...

Python学习之-正则表达式
目录 前言:1.re.serach1.1例子: 2.re.match2.1示例1:2.2 示例2: 3.re.findall3.1 示例 4.re.fullmatch4.1 示例1:4.2 示例2: 5.re.split5.1 示例1:5.2 示例2:5.3 示例3: 6.re.sub6.1 示例&#…...
Godot.NET C# 工程化开发(1):通用Nuget 导入+ 模板文件导出,包含随机数生成,日志管理,数据库连接等功能
文章目录 前言Github项目地址,包含模板文件后期思考补充项目设置编写失误环境visual studio 配置详细的配置看我这篇文章 Nuget 推荐NewtonSoft 成功Bogus 成功Github文档地址随机生成构造器生成构造器接口(推荐) 文件夹设置Nlog 成功!Nlog.configNlogHe…...

数据仓库——雪花模式以及层次递归
层次结构 钻取 向下钻取:对某些代表事实的报表中添加维度细节 向上钻取:从某些代表事实的报表中去除维度细节 属性层次 提供了一种自然方法,用于顺序地在不断深入的层次上组织事实。许多维度可以被理解为包含连续主从关系的属性层次。此类…...
Transformer的前世今生 day09(Transformer的框架概述)
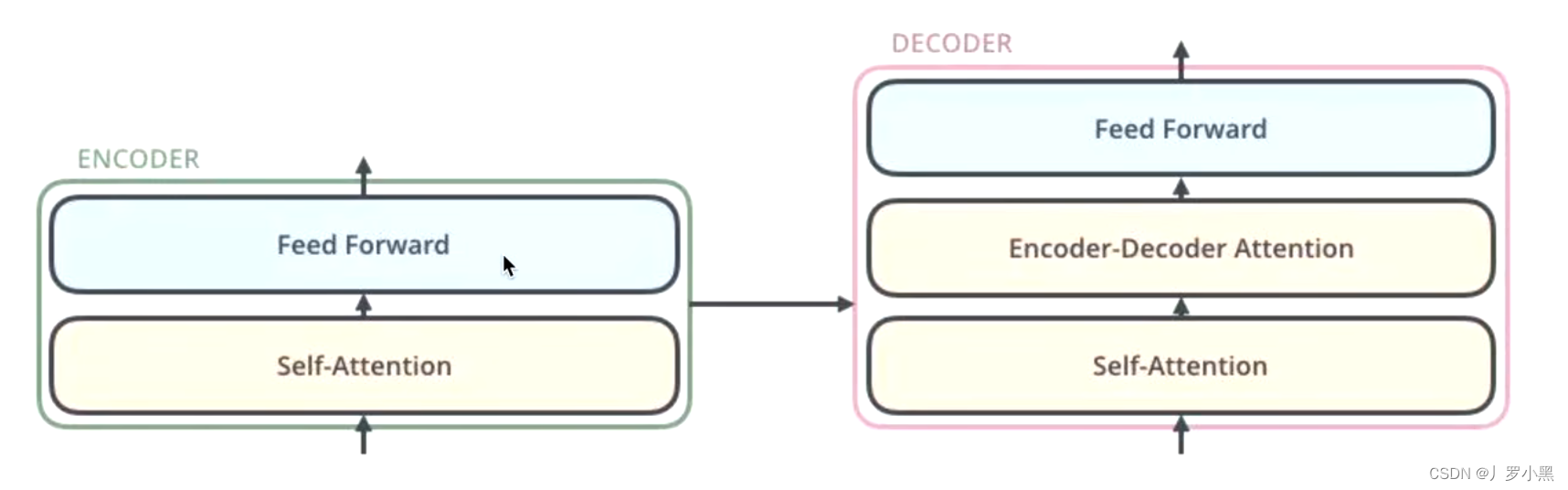
前情提要 编码器-解码器结构 如果将一个模型分为两块:编码器和解码器那么编码器-解码器结构为:编码器负责处理输入,解码器负责生成输出流程:我们先将输入送入编码器层,得到一个中间状态state,并送入解码器…...
Qt 压缩/解压文件
前面讲了很多Qt的文件操作,文件操作自然就包括压缩与解压缩文件了,正好最近项目里要用到压缩以及解压缩文件,所以就研究了一下Qt如何压缩与解压缩文件。 QZipReader/QZipWriter QZipReader 和 QZipWriter 类提供了用于读取和写入 ZIP 格式文…...
——位运算+数学+一维动态规划+多维动态规划)
【leetcode刷题之路】面试经典150题(8)——位运算+数学+一维动态规划+多维动态规划
文章目录 20 位运算20.1 【位运算】二进制求和20.2 【位运算】颠倒二进制位20.3 【位运算】位1的个数20.4 【位运算】只出现一次的数字20.5 【哈希表】【位运算】只出现一次的数字 II20.6 【位运算】数字范围按位与 21 数学21.1 【双指针】回文数21.2 【数学】加一21.3 【数学】…...
JetBrains全家桶激活,分享 WebStorm 2024 激活的方案
大家好,欢迎来到金榜探云手! WebStorm公司简介 JetBrains 是一家专注于开发工具的软件公司,总部位于捷克。他们以提供强大的集成开发环境(IDE)而闻名,如 IntelliJ IDEA、PyCharm、和 WebStorm等。这些工具…...
Sublime 彻底解决中文乱码
1. 按ctrl,打开Console,输入如下代码: import urllib.request,os; pf Package Control.sublime-package; ipp sublime.installed_packages_path(); urllib.request.install_opener( urllib.request.build_opener( urllib.request.ProxyHand…...

复旦大学EMBA校友出席两会建言献策助力中国发展
阳春三月,备受瞩目的全国两会如期召开。期间,复旦大学EMBA多位校友作为第十四届全国人民代表大会代表、第十四届全国政协委员与全国各地代表共商国是。 无论是作为大型央企负责人,还是作为科创企业的中坚力量,复旦大学EM…...
virtualbox导入vdi
新建虚拟机 点击新建 输入新建属性 配置cpu和内存 虚拟硬盘 这里选择已有的vdi文件 摘要 这里点击完成 虚拟机添加成功 点击启动,启动虚拟机 注意 这个时候的ip,还是以前镜像的ip,如果两个镜像一起启动,则需要修 改ip地…...

【信号处理】基于DGGAN的单通道脑电信号增强和情绪检测(tensorflow)
关于 情绪检测,是脑科学研究中的一个常见和热门的方向。在进行情绪检测的分类中,真实数据不足,经常导致情绪检测模型的性能不佳。因此,对数据进行增强,成为了一个提升下游任务的重要的手段。本项目通过DCGAN模型实现脑…...

使用 Docker Compose 部署 Spring Boot 应用
使用 Docker Compose 部署 Spring Boot 应用 第一步:创建 Spring Boot 应用的 Dockerfile 在您的 Spring Boot 项目根目录中创建一个 Dockerfile。 编辑 Dockerfile,添加以下内容: # 基础镜像使用 OpenJDK FROM openjdk:11-jdk-slim# 维护者…...

nginx 正向代理 https
问题背景 因为网络环境受限,应用服务器无法直接访问外网,需要前置机上中转一下,这种情况可在应用服务器修改/etc/hosts文件指向前置机,在前置机上的nginx设置四层代理,从而出站。 方案 根据How to Use NGINX as an …...

vue3从其他页面跳转页面头部组件菜单el-menu菜单高亮
主要代码 import { ref, onMounted, watch } from vue; const activeIndex ref("/"); const route useRoute();onMounted(() > {updateActiveMenu(); });watch(() > route.path, updateActiveMenu);function updateActiveMenu() {// 根据路由更新activeMenu…...

python 条件循环语句
python 条件循环语句 一、条件控制语句1. Python3 条件控制2. if 语句3. if 嵌套4. match...case5. 注意: 二、循环控制语句1. Python3 循环语句2. while 循环3. 无限循环4. while 循环使用 else 语句5. 简单语句组6. for 语句7. for...else8. break 和 continue 语…...
CIM搭建实现发送消息的效果
目录 背景过程1、下载代码2、进行配置3、直接启动项目4、打开管理界面5、启动web客户端实例项目6、发送消息 项目使用总结 背景 公司项目有许多需要发送即时消息的场景,之前一直采用的是传统的websocket连接,它会存在掉线严重,不可重连&…...
C++第十三弹---内存管理(下)
✨个人主页: 熬夜学编程的小林 💗系列专栏: 【C语言详解】 【数据结构详解】【C详解】 目录 1、operator new与operator delete函数 1.1、operator new与operator delete函数 2、new和delete的实现原理 2.1、内置类型 2.2、自定义类型 …...
Python爬虫学习完整版
一、什么是爬虫 网络爬虫,是一种按照一定规则,自动抓取互联网信息的程序或者脚本。由于互联网数据的多样性和资源的有限性,根据用户需求定向抓取相关网页并分析也成为如今主流的爬取策略。 1 爬虫可以做什么 你可以爬取网络上的的图片&#…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...
