机器学习之决策树现成的模型使用
目录
须知
DecisionTreeClassifier
sklearn.tree.plot_tree
cost_complexity_pruning_path(X_train, y_train)
CART分类树算法
基尼指数
分类树的构建思想
对于离散的数据
对于连续值
剪枝策略
剪枝是什么
剪枝的分类
预剪枝
后剪枝
后剪枝策略体现之威斯康辛州乳腺癌数据集
剪枝策略选用
代码
须知
在代码实现之前,我们先要知道,sklearn里面的tree库中的一些关键模块
DecisionTreeClassifier
sklearn.tree.DecisionTreeClassifier它的作用是创建一个决策树分类器模型
源码:
class sklearn.tree.DecisionTreeClassifier(*, criterion='gini', splitter='best', max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None, random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, class_weight=None, presort='deprecated', ccp_alpha=0.0)我们只需要了解关键参数就好
criterion:这个参数是用来选择使用何种方法度量树的切分质量的,也就是一个选择算法的。
当criterion取值为“gini”时采用 基尼不纯度(Gini impurity)算法构造决策树,当criterion取值为 “entropy” 时采用信息增益( information gain)算法构造决策树,默认为“gini”
splitter:此参数决定了在每个节点上拆分策略的选择。
支持的策略是“best” 选择“最佳拆分策略”, “random” 选择“最佳随机拆分策略”,这个先不做解释,只知道我们默认是“best”就好
max_depth:树的最大深度,取值应当是int类型,如果取值为None,则将所有节点展开,直到所有的叶子都是纯净的或者直到所有叶子都包含少于min_samples_split个样本。
min_samples_split:拆分内部节点所需的最少样本数:
· 如果取值 int , 则将min_samples_split视为最小值。
· 如果为float,则min_samples_split是一个分数,而ceil(min_samples_split * n_samples)是每个拆分的最小样本数。
默认为2
min_samples_leaf:在叶节点(就是我们的树最终的类别)处所需的最小样本数。 仅在任何深度的分裂点在左分支和右分支中的每个分支上至少留有min_samples_leaf个训练样本时,才考虑。 这可能具有平滑模型的效果,尤其是在回归中。
· 如果为int,则将min_samples_leaf视为最小值
· 如果为float,则min_samples_leaf是一个分数,而ceil(min_samples_leaf * n_samples)是每个节点的最小样本数。
默认为1
ccp_alpha:用于最小化成本复杂性修剪的复杂性参数。 将选择在成本复杂度小于ccp_alpha的子树中最大的子树。 默认情况下,不执行修剪。 有关详细信息,请参见最小成本复杂性修剪。
默认为0.0
了解以上就好了,剩下的可以自行Sklearn 中文社区了解。
sklearn.tree.plot_tree
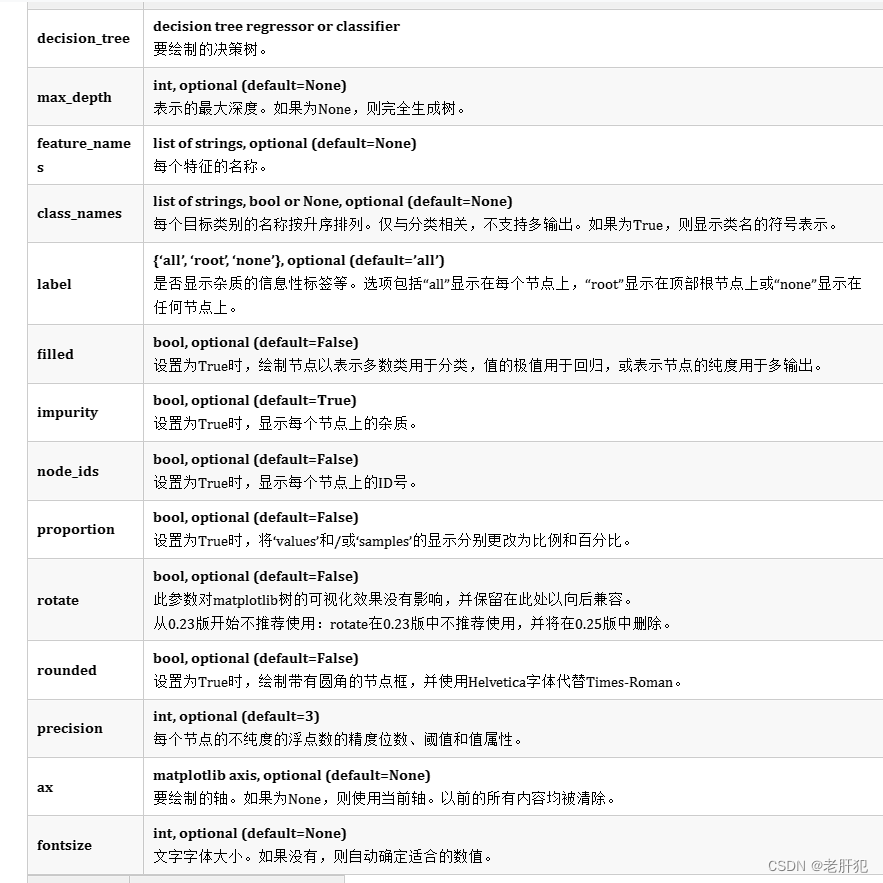
sklearn.tree.plot_tree(decision_tree, *, max_depth=None, feature_names=None, class_names=None, label='all', filled=False, impurity=True, node_ids=False, proportion=False, rotate='deprecated', rounded=False, precision=3, ax=None, fontsize=None)
 (上面图片来自于Sklearn中文社区)
(上面图片来自于Sklearn中文社区)
我们只需要记一下常用的就好,比如
feature_names 特征名称的列表,class_names 分类名称的列表(我用列表尝试的是可以的,但是不知道数组或者元组可以不可以,大家可以尝试一下)
另外我们还需要注意:
cost_complexity_pruning_path(X_train, y_train)
他的使用方法如下:
X, y = load_breast_cancer(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)clf = DecisionTreeClassifier(random_state=0)
path = clf.cost_complexity_pruning_path(X_train, y_train)
ccp_alphas, impurities = path.ccp_alphas, path.impurities官方的解释是:scikit-learn提供了DecisionTreeClassifier.cost_complexity_pruning_path在修剪过程中每一步返回有效的alphas和相应的总叶子不存度。随着alpha的增加,更多的树被修剪,这增加了它的叶子的总不存度。
意思是,cost_complexity_pruning_path(X_train, y_train)是DecisionTreeClassifier(random_state=0)模型里面封装的一个功能模块,我们可以通过这个模型的对象或者说实例化,来调用这个功能,他可以返回在我们这个数据集分类的树,在修剪过程中每一步有效的‘阿尔法’,(没错,alpha就是我们的‘阿尔法’,这是一个参数,用于衡量代价与复杂度之间关系)以及每一步的‘阿尔法’所对应的树的不纯度(用对应不太严谨,应该说每一步最终得到的树的不纯度)。
CART分类树算法
续博客:
决策树算法原理以及ID3、C4.5、CART算法
在上一篇博客中,我们只是提了一下cart分类树的基本算法“基尼算法”,这个算法的核心就是“基尼系数”。
基尼指数
关于基尼系数(基尼指数):

上面是计算样本的基尼指数。

分类树的构建思想
对于离散的数据
我们一开始选择树的根节点的时候,是把基尼指数最小的特征和该特征的最优切分点给选好的。看“西瓜书”里面的样例。
有些糊但是还可以,我们不需要知道原先的数据集,我们只是看一下,找根节点的思想就好了
就是把每个特征的最小的基尼指数的特征值拉出来,然后比较他们的基尼指数找到最小的特征值,那么这个特征值所属的特征就是根节点,而该特征值就是划分点。

分好根节点之后,我们根据划分点,把是该特征值的分为一类,作为叶子节点。(在叶子节点中,哪个种类的样本多,该叶子节点就是哪一类)
其他的分为另一类 ,然后接着按照之前的步骤接着分,循环往复,最后得到的其实是一个二叉树。
对于连续值
有的时候我们的特征值是连续的数据,就比如特征“金钱数额”,它对应的特征值是一个个的数值,所以这时候就需要其他的处理方法。(截图内容来自知乎)

简而言之,就是把连续 转化为离散,然后其他的就和离散的数据的处理方法一样,最后的到一个二叉树。
剪枝策略
剪枝是什么
剪枝顾名思义就是减去树的多余的“枝叶”,在我们的决策树里体现为,把一些子节点的叶节点去掉,让子节点成为叶节点
剪枝的分类
剪枝主要分为,预剪枝,后剪枝。
后剪枝的方法很多,现在说一些我们常用的:错误率降低剪枝REP(Reduced-Error Pruning)、悲观错误剪枝PEP(Pesimistic-Error Pruning)、代价复杂度剪枝CCP(Cost Complexity Pruning)、最小错误剪枝MEP。
预剪枝
预剪枝就是在我们构建树的每个节点前,都要计算样本的准确度有没有提升,没有提升我们就不构建,换一个划分点,提升了就接着划分。
具体原理推荐大家看一下这位网友在知乎的这篇博客:决策树总结(三)剪枝
(我们主要分析后剪枝)
预剪枝实例 思路:先用默认值,让树完整生长,再参考完全生长的决策树的信息,分析树有没有容易过拟合的表现,通过相关参数,对过分生长的节点作出限制,以新参数重新训练决策树。
的确 ,并没有体现出预剪枝的思想,但是没办法,这个方法其实我们真不常用,现成的模型中基本都是后剪枝。
后剪枝
代价复杂度剪枝CCP:同CART剪枝算法(最常用)。
错误率降低剪枝REP:划分训练集-验证集。训练集用于形成决策树;验证集用来评估修剪决策树。大致流程可描述为:对于训练集上构建的过拟合决策树,自底向上遍历所有子树进行剪枝,直到针对交叉验证数据集无法进一步降低错误率为止。
悲观错误剪枝PEP:悲观错误剪枝也是根据剪枝前后的错误率来决定是否剪枝,和REP不同的是,PEP不需要使用验证样本,并且PEP是自上而下剪枝的。
最小错误剪枝MEP:MEP 希望通过剪枝得到一棵相对于独立数据集来说具有最小期望错误率的决策树。所使用的独立数据集是用来简化对未知样本的错分样本率的估计的,并不意味真正使用了独立的剪枝集 ,实际情况是无论早期版本还是改进版本均只利用了训练集的信息。
CCP算法:为子树Tt定义了代价和复杂度,以及一个衡量代价与复杂度之间关系的参数a。其中代价指的是在剪枝过程中因子树T_t被叶节点替代而增加的错分样本;复杂度表示剪枝后子树Tt减少的叶结点数;a则表示剪枝后树的复杂度降低程度与代价间的关系。在树构建完成后,对树进行剪枝简化,使以下损失函数最小化:  损失函数既考虑了代价,又考虑了树的复杂度,所以叫代价复杂度剪枝法,实质就是在树的复杂度与准确性之间取得一个平衡点。 备注:在sklearn中,如果criterion设为gini,Li 则是每个叶子节点的gini系数,如果设为entropy,则是熵。
损失函数既考虑了代价,又考虑了树的复杂度,所以叫代价复杂度剪枝法,实质就是在树的复杂度与准确性之间取得一个平衡点。 备注:在sklearn中,如果criterion设为gini,Li 则是每个叶子节点的gini系数,如果设为entropy,则是熵。
后剪枝策略体现之威斯康辛州乳腺癌数据集
剪枝策略选用
CCP算法
代码
from matplotlib import font_manager
from sklearn import datasets # 导入数据集
from sklearn import tree
from sklearn.model_selection import \train_test_split # 导入数据分离包 用法:X_train,X_test, y_train, y_test = train_test_split(train_data, train_target, test_size, random_state, shuffle)
import numpy
import matplotlib.pyplot as pltdata = datasets.load_breast_cancer()
#print(data)
#key=data.keys()
#print(key) #dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename', 'data_module'])
sample=data['data']
#print(sample)
#print(sample.shape)#(569, 30) 一共569行 每行数据都有30个特征
#print(data['target'])
target=data['target']
#print(target)
# [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
# 1 0 0 0 0 0 0 0 0 1 0 1 1 1 1 1 0 0 1 0 0 1 1 1 1 0 1 0 0 1 1 1 1 0 1 0 0
# 1 0 1 0 0 1 1 1 0 0 1 0 0 0 1 1 1 0 1 1 0 0 1 1 1 0 0 1 1 1 1 0 1 1 0 1 1
# 1 1 1 1 1 1 0 0 0 1 0 0 1 1 1 0 0 1 0 1 0 0 1 0 0 1 1 0 1 1 0 1 1 1 1 0 1
# 1 1 1 1 1 1 1 1 0 1 1 1 1 0 0 1 0 1 1 0 0 1 1 0 0 1 1 1 1 0 1 1 0 0 0 1 0
# 1 0 1 1 1 0 1 1 0 0 1 0 0 0 0 1 0 0 0 1 0 1 0 1 1 0 1 0 0 0 0 1 1 0 0 1 1
# 1 0 1 1 1 1 1 0 0 1 1 0 1 1 0 0 1 0 1 1 1 1 0 1 1 1 1 1 0 1 0 0 0 0 0 0 0
# 0 0 0 0 0 0 0 1 1 1 1 1 1 0 1 0 1 1 0 1 1 0 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1
# 1 0 1 1 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0 1 0 1 1 1 1 0 0 0 1 1
# 1 1 0 1 0 1 0 1 1 1 0 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 1 1 1 0 0 1 0 0
# 0 1 0 0 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 0 1 1 0 0 1 1 1 1 1 1 0 1 1 1 1 1 1
# 1 0 1 1 1 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 0 0 1 0 1 1 1 1 1 0 1 1
# 0 1 0 1 1 0 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 0 1
# 1 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 1 0 0 1 0 1 0 1 1 1 1 1 0 1 1 0 1 0 1 0 0
# 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 0 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
# 1 1 1 1 1 1 1 0 0 0 0 0 0 1]
#print(data['target_names'])#['malignant' 'benign']三种类型分别对应:0,1#b=[0.05,0.1,0.15,0.2,0.25,0.3,0.35,0.4,0.45,0.5,0.55,0.6,0.75]
#b = [0.05,0.06,0.07,0.08, 0.1,0.11,0.12,0.13,0.14, 0.15,0.16,0.17,0.18,0.19,0.2, 0.21, 0.22,0.25,0.27,0.29 ,0.3,0.33, 0.35,0.37, 0.4,0.45,0.5]
# b = [0.01,0.02,0.03,0.05,0.06,0.07,0.08,0.09, 0.1]
# a = []
# for x in b:
# train_data,test_data,train_target,test_target=train_test_split(sample,target,test_size=x,random_state=2020)
# tree_= tree.DecisionTreeClassifier()
# tree_.fit(train_data,train_target)
# print('模型的准确度:',tree_.score(test_data,test_target))
# a.append(tree_.score(test_data,test_target))
# plt.plot(b,a)
# plt.show()
#测试集尺寸选择0.03比较合适
#开始创建模型
train_data, test_data, train_target, test_target = train_test_split(sample, target, test_size=0.03, random_state=2020)
tree_ = tree.DecisionTreeClassifier()
tree_.fit(train_data, train_target)
print('模型准确度:',tree_.score(test_data, test_target))
tree.plot_tree(tree_,filled=True,feature_names=data['feature_names'],class_names=data['target_names'])
plt.show()
print('在叶子节点对应的索引---------------------')
print(tree_.apply(sample))
print( '预测-----------------------')
# [1.799e+01 1.038e+01 1.228e+02 1.001e+03 1.184e-01 2.776e-01 3.001e-01
# 1.471e-01 2.419e-01 7.871e-02 1.095e+00 9.053e-01 8.589e+00 1.534e+02
# 6.399e-03 4.904e-02 5.373e-02 1.587e-02 3.003e-02 6.193e-03 2.538e+01
# 1.733e+01 1.846e+02 2.019e+03 1.622e-01 6.656e-01 7.119e-01 2.654e-01
# 4.601e-01 1.189e-01],0
b = [sample[0]]
b_target = tree_.predict(b)
print(b_target)
# # 优化:
# #优化方式一:从整个树开始处理一些枝节
print('从整个树开始处理一些枝节--------------------------------')
tree_ = tree.DecisionTreeClassifier(min_samples_leaf=15,random_state=0)
tree_.fit(train_data, train_target)
tree.plot_tree(tree_,filled=True,feature_names=data['feature_names'],class_names=data['target_names'])
plt.show()
print('模型准确度:',tree_.score(test_data, test_target))
print('在叶子节点对应的索引---------------------')
print(tree_.apply(sample))
# print( '预测-----------------------')
# [1.799e+01 1.038e+01 1.228e+02 1.001e+03 1.184e-01 2.776e-01 3.001e-01
# 1.471e-01 2.419e-01 7.871e-02 1.095e+00 9.053e-01 8.589e+00 1.534e+02
# 6.399e-03 4.904e-02 5.373e-02 1.587e-02 3.003e-02 6.193e-03 2.538e+01
# 1.733e+01 1.846e+02 2.019e+03 1.622e-01 6.656e-01 7.119e-01 2.654e-01
# 4.601e-01 1.189e-01],0
b = [sample[0]]
b_target = tree_.predict(b)
print(b_target)
# #优化方式二:后剪枝cpp
print('后剪枝cpp------------------')
tree_ = tree.DecisionTreeClassifier(min_samples_leaf=15,random_state=0)
tree_.fit(train_data, train_target)
impuritiesandalphas=tree_.cost_complexity_pruning_path(train_data,train_target)
impurities=impuritiesandalphas.impurities
alphas=impuritiesandalphas.ccp_alphas
print('impurities',impurities)
print('alphas',alphas)
print('开始后剪枝训练------------------')
# test_=[0. , 0.00046032 ,0.000881 , 0.00194334, 0.01499473, 0.0181062,0.04895626 ,0.32369286]
# test_=[0. , 0.00046032 ,0.000881 , 0.00194334, 0.01499473, 0.0181062,0.04895626]
# test_=[0. , 0.00046032 ,0.000881 , 0.00194334, 0.01499473, 0.0181062,0.02]
# scor_=[]
# for x in test_:
# tree_ = tree.DecisionTreeClassifier(min_samples_leaf=5,random_state=0,ccp_alpha=x)
# tree_.fit(train_data, train_target)
# print('模型准确度:',tree_.score(test_data, test_target))
# scor_.append(tree_.score(test_data, test_target))
# font = font_manager.FontProperties(fname="C:\\Users\\ASUS\\Desktop\\Fonts\\STZHONGS.TTF")
# plt.plot(test_, scor_, "r", label='模型精准度')
# plt.title('参数alpha和模型精准度的关系', fontproperties=font, fontsize=18)
# plt.legend(prop=font)
# plt.show()
#alpha=0.02
al=0.02
tree_ = tree.DecisionTreeClassifier(min_samples_leaf=15,random_state=0,ccp_alpha=al)
tree_.fit(train_data, train_target)
tree.plot_tree(tree_,filled=True,feature_names=data['feature_names'],class_names=data['target_names'])
plt.show()
print('模型准确度:',tree_.score(test_data, test_target))
print('在叶子节点对应的索引---------------------')
print(tree_.apply(sample))
print(f'alpha={al}时树的纯度:')
is_leaf =tree_.tree_.children_left ==-1
tree_impurities = (tree_.tree_.impurity[is_leaf]* tree_.tree_.n_node_samples[is_leaf]/len(train_target)).sum()
print(tree_impurities)
print( '预测-----------------------')
# [1.799e+01 1.038e+01 1.228e+02 1.001e+03 1.184e-01 2.776e-01 3.001e-01
# 1.471e-01 2.419e-01 7.871e-02 1.095e+00 9.053e-01 8.589e+00 1.534e+02
# 6.399e-03 4.904e-02 5.373e-02 1.587e-02 3.003e-02 6.193e-03 2.538e+01
# 1.733e+01 1.846e+02 2.019e+03 1.622e-01 6.656e-01 7.119e-01 2.654e-01
# 4.601e-01 1.189e-01],0
b = [sample[0]]
b_target = tree_.predict(b)
print(b_target)
总之我们要根据模型生成的树来进行剪枝判断,从而更改模型参数。
相关文章:

机器学习之决策树现成的模型使用
目录 须知 DecisionTreeClassifier sklearn.tree.plot_tree cost_complexity_pruning_path(X_train, y_train) CART分类树算法 基尼指数 分类树的构建思想 对于离散的数据 对于连续值 剪枝策略 剪枝是什么 剪枝的分类 预剪枝 后剪枝 后剪枝策略体现之威斯康辛州乳…...
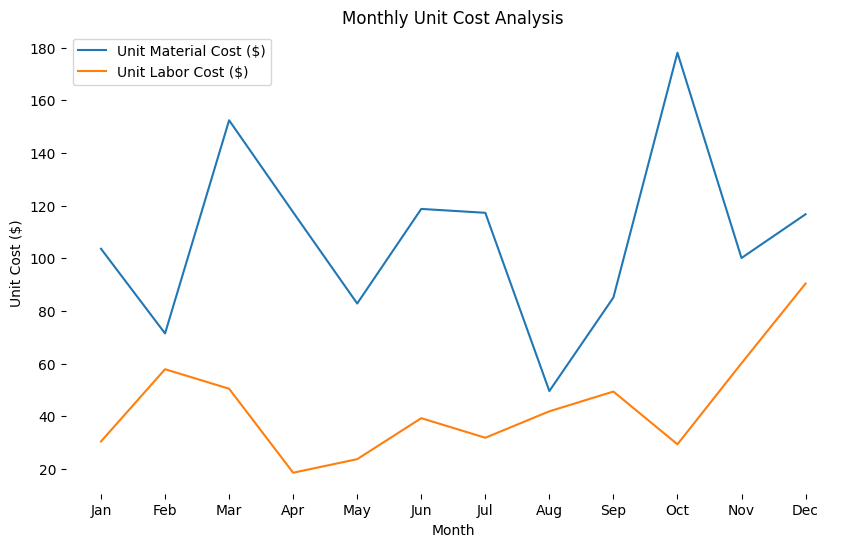
【python分析实战】成本:揭示电商平台月度开支与成本结构占比 - 过于详细 【收藏】
重点关注本文思路,用python分析,方便大家实验复现,代码每次都用全量的,其他工具自行选择。 全文3000字,阅读10min,操作1小时 企业案例实战欢迎关注专栏 每日更新:https://blog.csdn.net/cciehl/…...

新网站收录时间是多久,新建网站多久被百度收录
对于新建的网站而言,被搜索引擎收录是非常重要的一步,它标志着网站的正式上线和对外开放。然而,新网站被搜索引擎收录需要一定的时间,而且时间长短受多种因素影响。本文将探讨新网站收录需要多长时间,以及新建网站多久…...
通过Caliper进行压力测试程序,且汇总压力测试问题解决
环境要求 第一步. 配置基本环境 部署Caliper的计算机需要有外网权限;操作系统版本需要满足以下要求:Ubuntu >= 16.04、CentOS >= 7或MacOS >= 10.14;部署Caliper的计算机需要安装有以下软件:python 2.7、make、g++(gcc-c++)、gcc及git。第二步. 安装NodeJS # …...

LabVIEW比例流量阀自动测试系统
LabVIEW比例流量阀自动测试系统 开发了一套基于LabVIEW编程和PLC控制的比例流量阀自动测试系统。通过引入改进的FCMAC算法至测试回路的压力控制系统,有效提升了压力控制效果,展现了系统的设计理念和实现方法。 项目背景: 比例流量阀在液压…...

安卓U3D逆向从Assembly-CSharp到il2cpp
随着unity技术的发展及厂商对于脚本源码的保护,很大一部分U3D应用的scripting backend已经由mono转为了il2cpp,本文从unity简单应用的制作讲起,介绍U3D应用脚本的Assembly-CSharp.dll的逆向及il2cpp.so的逆向分析。 目录如下: 0…...

计算机网络——30SDN控制平面
SDN控制平面 SDN架构 数据平面交换机 快速、简单,商业化交换设备采用硬件实现通用转发功能流表被控制器计算和安装基于南向API,SDN控制器访问基于流的交换机 定义了哪些可以被控制哪些不能 也定义了和控制器的协议 SDN控制器(网络OS&#…...
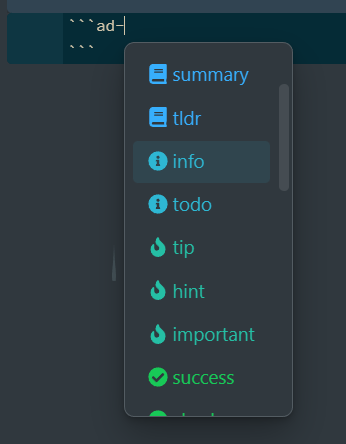
Obsidian插件-高亮块(Admonition)
在插件市场里面搜索Admonition并安装插件,就可以使用高亮块了。 添加高亮块 用法稍微有一些不同。按照下面的格式,输入Markdown就可以创建一个高亮块。 内容内容内容输入*ad-*会出现相应的类型可以选择...

jHipster 之 webflux-前端用EventSource处理sse变成了批量处理而非实时处理
现象: const eventSource new EventSource(API_URL5);eventSource.onmessage streamEvent > {console.log(a message is come in--------->);const content streamEvent.data;console.log(Received content: content);};前端用EventSource 处理webflux的…...
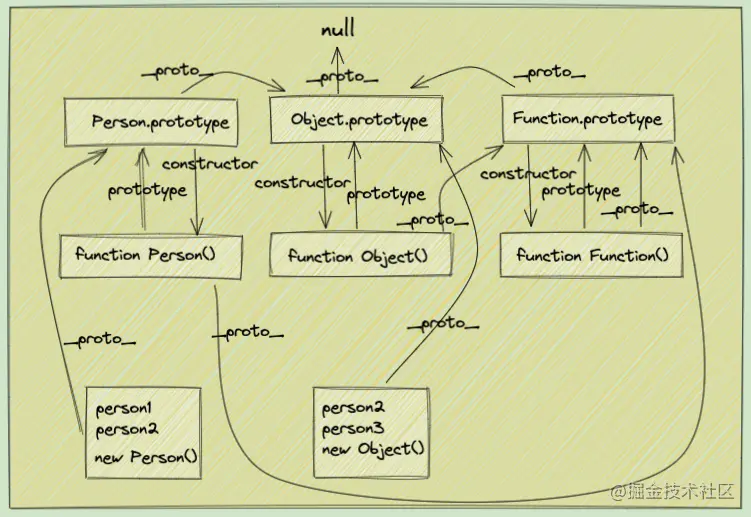
原型链-(前端面试 2024 版)
来讲一讲原型链 原型链只存在于函数之中 四个规则 1、引用类型,都具有对象特性,即可自由扩展属性。 2、引用类型,都有一个隐式原型 __proto__ 属性,属性值是一个普通的对象。 3、引用类型,隐式原型 __proto__ 的属…...

网络套接字补充——UDP网络编程
五、UDP网络编程 1.对于服务器使用智能指针维护生命周期;2.创建UDP套接字;3.绑定端口号,包括设置服务器端口号和IP地址,端口号一般是2字节使用uint16_t,而IP地址用户习惯使用点分十进制格式所以传入的是string类型…...

自动化测试 —— Pytest fixture及conftest详解
前言 fixture是在测试函数运行前后,由pytest执行的外壳函数。fixture中的代码可以定制,满足多变的测试需求,包括定义传入测试中的数据集、配置测试前系统的初始状态、为批量测试提供数据源等等。fixture是pytest的精髓所在,类似u…...
)
Scala第十四章节(隐式转换、隐式参数以及获取列表元素平均值的案例)
章节目标 掌握隐式转换相关内容掌握隐式参数相关内容掌握获取列表元素平均值的案例 1.隐式转换和隐式参数介绍 隐式转换和隐式参数是Scala中非常有特色的功能,也是Java等其他编程语言没有的功能。我们可以很方便地利用 隐式转换来丰富现有类的功能。在后续编写Ak…...
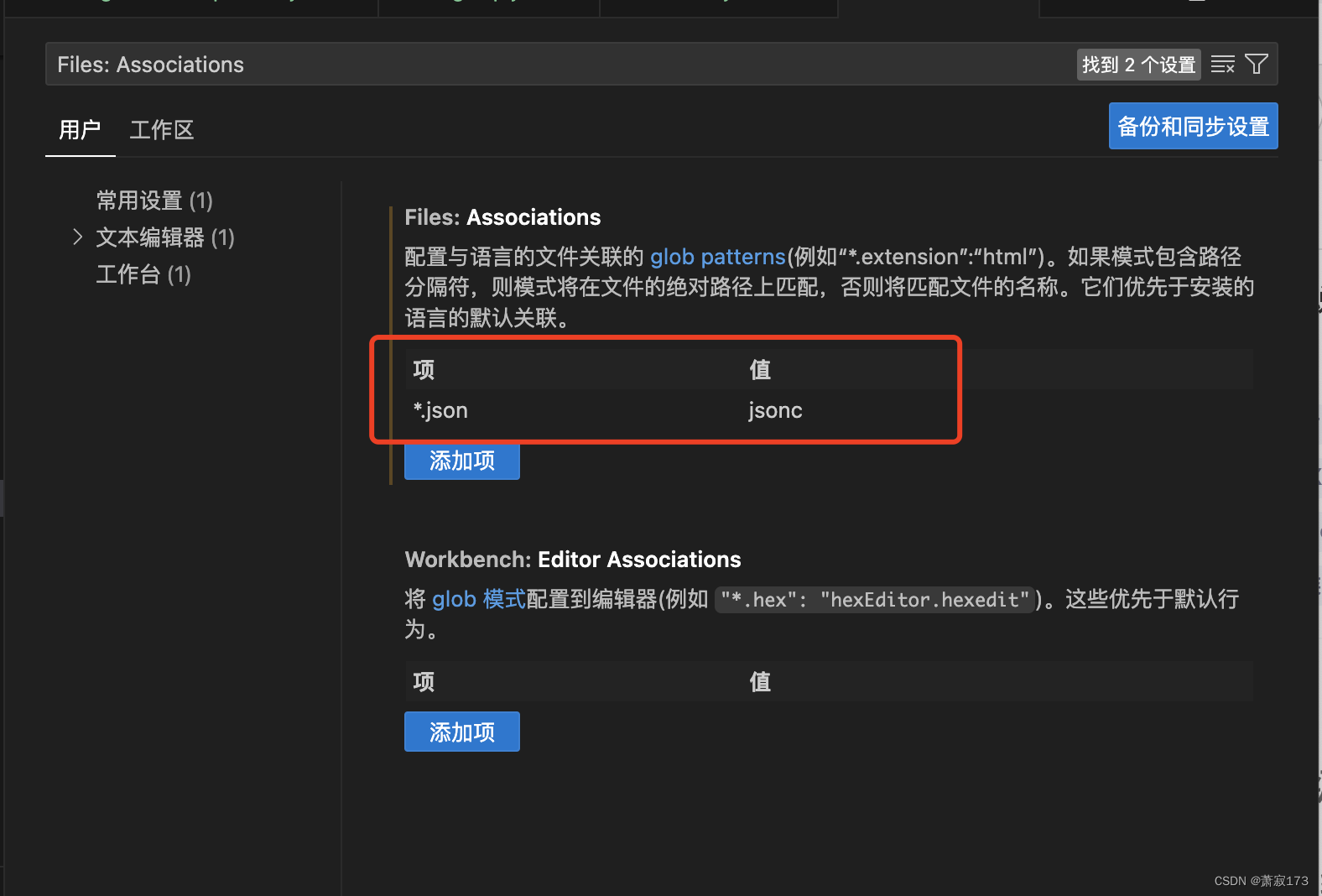
VsCode的json文件不允许注释的解决办法
右下角找到注释点进去 输入Files: Associations搜索出此项 改为项为*.json值为jsonc保存即可 然后会发现VsCode的json文件就允许注释了...

利用图像识别进行疾病诊断
利用图像识别进行疾病诊断是人工智能和机器学习技术在医疗领域的一个重要应用。图像识别技术可以通过分析医学影像(如X光片、CT扫描、MRI、超声波图像等)来辅助医生诊断疾病。以下是图像识别在疾病诊断中的关键步骤和挑战: 数据收集与预处理…...

大数据学习-2024/3/28-excel文件的读写操作
借助第三方模块:inxlrd,xlwt pip 第三方模块包管理工具 –> winr --> cmd --> 打开操作系统 –> python --> 查看默认的解释器版本 --> exit() –> pip list --> 查看第三方模块的列表 pip36 list --> 查看3.6版本安装的第三方模块列表 –> pip[…...

k8s 如何获取加入节点命名
当k8s集群初始化成功的时候,就会出现 加入节点 的命令如下: 但是如果忘记了就需要找回这条命令了。 kubeadm join 的命令格式如下:kubeadm join --token <token> --discovery-token-ca-cert-hash sha256:<hash>--token 令牌--…...
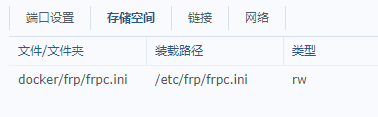
黑群晖基于docker配置frp内网穿透
前言 我的黑群晖需要设置一下内网穿透来外地访问,虽然zerotier的p2p组网已经很不错了,但是这个毕竟有一定的局限性,比如我是ios的国区id就下载不了zerotier的app,组网不了 1.下载镜像 选择第一个镜像 2.映射文件 配置frpc.ini&a…...

多线程基础:线程通信内容补充
多线程基础:线程通信内容补充 文章目录 多线程基础:线程通信内容补充前言一、wait(), notify(), notifyAll()二、join()三、Lock 和 Condition四、并发集合和原子变量1、并发集合2、原子变量 总结 前言 前文内容中讲了线程通信的内容,但是不…...
使用Jenkins打包时执行失败,但手动执行没有问题如ERR_ELECTRON_BUILDER_CANNOT_EXECUTE
具体错误信息如: Error output: Plugin not found, cannot call UAC::_ Error in macro _UAC_MakeLL_Cmp on macroline 2 Error in macro _UAC_IsInnerInstance on macroline 1 Error in macro _If on macroline 9 Error in macro FUNCTION_INSTALL_MODE_PAGE_FUNC…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...
