Java八股文(数据结构)
Java八股文の数据结构
- 数据结构
数据结构
- 请解释以下数据结构的概念:链表、栈、队列和树。
链表是一种线性数据结构,由节点组成,每个节点包含了指向下一个节点的指针;
栈是一种后进先出(LIFO)的数据结构,只能在一端进行插入和删除操作;
队列是一种先进先出(FIFO)的数据结构,一端进行插入操作,在另一端进行删除操作;
树是一种非线性数据结构,由节点和边组成,其中父节点可以有多个子节点。
- 请解释下面时间复杂度符号的含义:O(1)、O(log n)、O(n)和O(n^2)。
O(1)表示算法的执行时间不随输入规模变化;
O(log n)表示算法的执行时间随输入规模的增加而增加,但增加速度较慢;
O(n)表示算法的执行时间与输入规模成正比;
O(n^2)表示算法的执行时间与输入规模的平方成正比。
- 请解释什么是二分查找,并提供一个二分查找的实现。
二分查找是一种在有序数组中查找元素的算法,每次都将区间缩小为原来的一半,直到找到目标元素或无法再缩小。
以下是一个二分查找的实现(Java):
public int binarySearch(int[] arr, int target) {int left = 0;int right = arr.length - 1;while (left <= right) {int mid = left + (right - left) / 2;if (arr[mid] == target) {return mid;} else if (arr[mid] < target) {left = mid + 1;} else {right = mid - 1;}}return -1;
}
- 请解释什么是哈希表,并提供一个哈希函数的示例。
哈希表是一种基于哈希函数的数据结构,用于存储和查找键值对。
哈希函数将键映射为一个固定大小的数组索引,使得在查找或插入时可以快速定位。
以下是一个哈希函数的示例(Java):
public int hashFunction(String key) {int hash = 0;for (int i = 0; i < key.length(); i++) {hash = (hash + key.charAt(i) - 'a') % tableSize;}return hash;
}
在此示例中,假设我们将英文字母映射为整数,'a’对应0,'b’对应1,以此类推。
- 请解释什么是二叉树,并提供一个二叉树的遍历实现(前序、中序和后序)。
二叉树是一种特殊的树结构,每个节点最多有两个子节点,称为左子节点和右子节点。
以下是二叉树的前序、中序和后序遍历的实现(Java):
// 前序遍历(根-左-右)
public void preOrderTraversal(TreeNode root) {if (root == null) {return;}System.out.println(root.val);preOrderTraversal(root.left);preOrderTraversal(root.right);
}// 中序遍历(左-根-右)
public void inOrderTraversal(TreeNode root) {if (root == null) {return;}inOrderTraversal(root.left);System.out.println(root.val);inOrderTraversal(root.right);
}// 后序遍历(左-右-根)
public void postOrderTraversal(TreeNode root) {if (root == null) {return;}postOrderTraversal(root.left);postOrderTraversal(root.right);System.out.println(root.val);
}
这里的TreeNode是二叉树的节点类,包含一个值val和左右子节点的引用。
- 请解释什么是图,并提供一种图的表示方法。
图是一种非线性数据结构,由节点(顶点)和边组成,表示顶点之间的关系。
常用的图的表示方法有邻接矩阵和邻接表。
邻接矩阵使用二维数组表示节点之间的连接关系,而邻接表则使用链表数组表示每个节点的邻居。
- 请解释什么是堆,并提供一个堆的实现。
堆是一种完全二叉树,分为最大堆和最小堆。
最大堆中,每个父节点的值都大于或等于其子节点的值;
最小堆中,每个父节点的值都小于或等于其子节点的值。
以下是一个最大堆的实现(Java):
class MaxHeap {private int[] heap;private int size;public MaxHeap(int capacity) {heap = new int[capacity];size = 0;}public void insert(int value) {if (size == heap.length) {throw new IllegalStateException("Heap is full");}heap[size] = value;siftUp(size);size++;}private void siftUp(int index) {while (index > 0 && heap[index] > heap[parentIndex(index)]) {swap(index, parentIndex(index));index = parentIndex(index);}}public int removeMax() {if (size == 0) {throw new IllegalStateException("Heap is empty");}int max = heap[0];heap[0] = heap[size - 1];size--;siftDown(0);return max;}private void siftDown(int index) {while (leftChildIndex(index) < size) {int maxIndex = leftChildIndex(index);if (rightChildIndex(index) < size && heap[rightChildIndex(index)] > heap[leftChildIndex(index)]) {maxIndex = rightChildIndex(index);}if (heap[index] >= heap[maxIndex]) {break;}swap(index, maxIndex);index = maxIndex;}}// Helper methods for calculating parent and child indicesprivate int parentIndex(int index) {return (index - 1) / 2;}private int leftChildIndex(int index) {return 2 * index + 1;}private int rightChildIndex(int index) {return 2 * index + 2;}private void swap(int index1, int index2) {int temp = heap[index1];heap[index1] = heap[index2];heap[index2] = temp;}
}
该堆类提供了插入和删除最大值的操作,并保持了堆的性质。
- 请解释什么是哈夫曼树,并提供一个哈夫曼编码的实现。
哈夫曼树是一种用于数据编码的树结构,用于将频率较高的字符编码为较短的二进制码,以实现更高的压缩比。
哈夫曼编码的实现需要构建哈夫曼树,并通过DFS遍历树来生成每个字符的编码。
以下是一个哈夫曼编码的实现(Java):
class HuffmanNode implements Comparable<HuffmanNode> {char value;int frequency;HuffmanNode left;HuffmanNode right;public HuffmanNode(char value, int frequency) {this.value = value;this.frequency = frequency;}@Overridepublic int compareTo(HuffmanNode other) {return this.frequency - other.frequency;}
}public String huffmanEncode(String text) {if (text.isEmpty()) {return "";}// Calculate character frequenciesMap<Character, Integer> frequencies = new HashMap<>();for (char c : text.toCharArray()) {frequencies.put(c, frequencies.getOrDefault(c, 0) + 1);}// Build Huffman treePriorityQueue<HuffmanNode> pq = new PriorityQueue<>();for (Map.Entry<Character, Integer> entry : frequencies.entrySet()) {pq.offer(new HuffmanNode(entry.getKey(), entry.getValue()));}while (pq.size() > 1) {HuffmanNode left = pq.poll();HuffmanNode right = pq.poll();HuffmanNode merged = new HuffmanNode('-', left.frequency + right.frequency);merged.left = left;merged.right = right;pq.offer(merged);}// Generate Huffman codesMap<Character, String> codes = new HashMap<>();generateCodes(pq.peek(), "", codes);// Encode the textStringBuilder encodedText = new StringBuilder();for (char c : text.toCharArray()) {encodedText.append(codes.get(c));}return encodedText.toString();
}private void generateCodes(HuffmanNode node, String code, Map<Character, String> codes) {if (node == null) {return;}if (node.left == null && node.right == null) {codes.put(node.value, code);}generateCodes(node.left, code + "0", codes);generateCodes(node.right, code + "1", codes);
}
该示例中,huffmanEncode方法接受一个字符串,并返回其哈夫曼编码后的结果。
- 请解释深度优先搜索(DFS)和广度优先搜索(BFS)的区别。
DFS和BFS是两种图遍历的算法。
DFS以深度为优先,从起始节点开始,尽可能深入地访问其邻居节点,直到无法再深入为止,然后回溯到上一个节点。
BFS以广度为优先,从起始节点开始,依次访问同一层级的节点,再逐层向下一层级访问。
DFS适用于查找目标在树或图中的路径,而BFS适用于查找最短路径或查找目标在特定距离内的节点。
- 请解释什么是红黑树,并说明其性质。
红黑树是一种自平衡的二叉搜索树,具有以下性质:
● 每个节点是红色或黑色。
● 根节点是黑色。
● 每个叶子节点(NIL节点)是黑色。
● 如果一个节点是红色,则其子节点必须是黑色(不能有两个相邻的红色节点)。
● 从任一节点到其每个叶子的所有路径都包含相同数量的黑色节点。
- 请解释什么是AVL树,并说明其性质。
AVL树是一种自平衡的二叉搜索树,具有以下性质:
● 对于每个节点,其左子树和右子树的高度差(平衡因子)最多为1。
● 任意节点的左子树和右子树都是AVL树。
- 请解释什么是B树,并说明其特点。
B树是一种自平衡的多路搜索树,具有以下特点:
● 每个节点最多有M个子节点(M>=2)。
● 除根节点和叶子节点外,每个节点至少有M/2个子节点。
● 所有叶子节点都在同一层级上。
- 请解释什么是缓存淘汰策略,并提供两个常见的缓存淘汰策略。
缓存淘汰策略用于在缓存容量不足时确定哪些项目应从缓存中淘汰。
常见的缓存淘汰策略有:● 最近最少使用(Least Recently Used, LRU):淘汰最近最少使用的项目,即最长时间未被访问的项目。
● 最不常用(Least Frequently Used, LFU):淘汰使用频率最低的项目,即被访问次数最少的项目。
- 请解释什么是拓扑排序,并提供一个拓扑排序的实现。
拓扑排序是一种对有向无环图进行排序的算法,使得所有边的方向均从前向后。
以下是一个拓扑排序的实现(Java):
public List<Integer> topologicalSort(int numCourses, int[][] prerequisites) {List<Integer> sortedOrder = new ArrayList<>();if (numCourses <= 0) {return sortedOrder;}// 1. 构建图和入度数组Map<Integer, List<Integer>> graph = new HashMap<>();int[] inDegree = new int[numCourses];for (int i = 0; i < numCourses; i++) {graph.put(i, new ArrayList<>());}for (int[] prerequisite : prerequisites) {int parent = prerequisite[1];int child = prerequisite[0];graph.get(parent).add(child);inDegree[child]++;}// 2. 将入度为0的节点加入队列Queue<Integer> queue = new LinkedList<>();for (int i = 0; i < numCourses; i++) {if (inDegree[i] == 0) {queue.offer(i);}}// 3. 逐个从队列取出节点,减少相关节点的入度并判断是否入队while (!queue.isEmpty()) {int node = queue.poll();sortedOrder.add(node);List<Integer> children = graph.get(node);for (int child : children) {inDegree[child]--;if (inDegree[child] == 0) {queue.offer(child);}}}// 4. 判断是否存在环if (sortedOrder.size() != numCourses) {return new ArrayList<>();}return sortedOrder;
}
该方法接受课程数量和先修关系的二维数组,并返回一个拓扑有序的课程列表。
- 请解释什么是并查集,并提供一个并查集的实现。
并查集是一种用于解决集合合并和查询的数据结构,支持以下两种操作:
● 查找(Find):确定元素所属的集合。
● 合并(Union):将两个集合合并为一个集合。
以下是一个并查集的实现(Java):
class UnionFind {private int[] parent;private int[] rank;public UnionFind(int size) {parent = new int[size];rank = new int[size];for (int i = 0; i < size; i++) {parent[i] = i;rank[i] = 0;}}public int find(int x) {if (parent[x] != x) {parent[x] = find(parent[x]);}return parent[x];}public void union(int x, int y) {int rootX = find(x);int rootY = find(y);if (rootX != rootY) {if (rank[rootX] < rank[rootY]) {parent[rootX] = rootY;} else if (rank[rootX] > rank[rootY]) {parent[rootY] = rootX;} else {parent[rootY] = rootX;rank[rootX]++;}}}
}
该并查集类提供了查找和合并操作,并使用路径压缩和按秩合并的优化策略。
- 请解释什么是动态规划,并提供一个使用动态规划解决的问题示例。
动态规划(Dynamic Programming,简称DP)是一种解决多阶段决策最优化问题的方法。
它将问题划分为若干个子问题,并保存子问题的解来避免重复计算。
通过递推求解各个子问题,最终得到原问题的解。
一个典型的动态规划问题是求解最长公共子序列(Longest Common Subsequence,简称LCS)。
给定两个字符串s1和s2,求它们的最长公共子序列的长度。
示例:
public class LongestCommonSubsequence {public int longestCommonSubsequence(String text1, String text2) {int m = text1.length();int n = text2.length();int[][] dp = new int[m + 1][n + 1]; // dp[i][j]表示text1前i个字符和text2前j个字符的最长公共子序列长度for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {if (text1.charAt(i - 1) == text2.charAt(j - 1)) {dp[i][j] = dp[i - 1][j - 1] + 1; // 当前字符相等,最长公共子序列长度加1} else {dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]); // 当前字符不相等,取前一步的最优解}}}return dp[m][n];}
}
在这个示例中,使用动态规划求解了最长公共子序列的长度。
通过定义一个二维数组dp,其中dp[i][j]表示text1前i个字符和text2前j个字符的最长公共子序列长度。
在遍历字符串text1和text2时,根据字符是否相等来更新dp数组的值。
最终返回dp[m][n]即为最长公共子序列的长度。
动态规划的思想可以帮助我们高效地解决很多复杂的问题,包括字符串匹配、最短路径、背包问题等。
- 实现一个二叉树的前序遍历算法。
class TreeNode {int val;TreeNode left;TreeNode right;public TreeNode(int val) {this.val = val;}
}public class PreorderTraversal {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();if (root == null) {return result;}Stack<TreeNode> stack = new Stack<>();stack.push(root);while (!stack.isEmpty()) {TreeNode node = stack.pop();result.add(node.val);if (node.right != null) {stack.push(node.right);}if (node.left != null) {stack.push(node.left);}}return result;}
}
- 实现一个队列,并实现基本的操作:入队、出队、获取队首元素。
class MyQueue {private Stack<Integer> inStack;private Stack<Integer> outStack;public MyQueue() {inStack = new Stack<>();outStack = new Stack<>();}public void push(int x) {inStack.push(x);}public int pop() {if (outStack.isEmpty()) {while (!inStack.isEmpty()) {outStack.push(inStack.pop());}}return outStack.pop();}public int peek() {if (outStack.isEmpty()) {while (!inStack.isEmpty()) {outStack.push(inStack.pop());}}return outStack.peek();}public boolean empty() {return inStack.isEmpty() && outStack.isEmpty();}
}
- 实现一个栈,并实现基本的操作:入栈、出栈、获取栈顶元素、判断栈是否为空。
class MyStack {private Deque<Integer> stack;public MyStack() {stack = new LinkedList<>();}public void push(int x) {stack.push(x);}public int pop() {return stack.pop();}public int top() {return stack.peek();}public boolean empty() {return stack.isEmpty();}
}
- 实现一个链表的反转。
class ListNode {int val;ListNode next;public ListNode(int val) {this.val = val;}
}public class ReverseLinkedList {public ListNode reverseList(ListNode head) {ListNode prev = null;ListNode curr = head;while (curr != null) {ListNode next = curr.next;curr.next = prev;prev = curr;curr = next;}return prev;}
}
- 实现一个图的深度优先搜索(DFS)算法。
import java.util.ArrayList;
import java.util.List;class Graph {private int V;private List<List<Integer>> adj;public Graph(int V) {this.V = V;adj = new ArrayList<>(V);for (int i = 0; i < V; i++) {adj.add(new ArrayList<>());}}public void addEdge(int u, int v) {adj.get(u).add(v);}public void DFS(int v) {boolean[] visited = new boolean[V];DFSUtil(v, visited);}private void DFSUtil(int v, boolean[] visited) {visited[v] = true;System.out.print(v + " ");for (int i : adj.get(v)) {if (!visited[i]) {DFSUtil(i, visited);}}}
}
- 实现一个图的广度优先搜索(BFS)算法。
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;class Graph {private int V;private List<List<Integer>> adj;public Graph(int V) {this.V = V;adj = new ArrayList<>(V);for (int i = 0; i < V; i++) {adj.add(new ArrayList<>());}}public void addEdge(int u, int v) {adj.get(u).add(v);}public void BFS(int v) {boolean[] visited = new boolean[V];Queue<Integer> queue = new LinkedList<>();visited[v] = true;queue.offer(v);while (!queue.isEmpty()) {int curr = queue.poll();System.out.print(curr + " ");for (int i : adj.get(curr)) {if (!visited[i]) {visited[i] = true;queue.offer(i);}}}}
}
- 实现一个最小堆。
class MinHeap {private int[] heap;private int size;public MinHeap(int capacity) {heap = new int[capacity];size = 0;}public void insert(int key) {if (size == heap.length) {// 堆已满return;}size++;int i = size - 1;heap[i] = key;while (i > 0 && heap[parent(i)] > heap[i]) {// 交换节点值swap(i, parent(i));i = parent(i);}}public void delete(int key) {int index = -1;for (int i = 0; i < size; i++) {if (heap[i] == key) {index = i;break;}}if (index == -1) {// 不存在该元素return;}decreaseKey(index, Integer.MIN_VALUE);extractMin();}public int extractMin() {if (size == 0) {return Integer.MIN_VALUE;}if (size == 1) {size--;return heap[0];}int root = heap[0];heap[0] = heap[size - 1];size--;minHeapify(0);return root;}private void decreaseKey(int i, int newValue) {heap[i] = newValue;while (i != 0 && heap[parent(i)] > heap[i]) {swap(i, parent(i));i = parent(i);}}private void minHeapify(int i) {int smallest = i;int left = leftChild(i);int right = rightChild(i);if (left < size && heap[left] < heap[smallest]) {smallest = left;}if (right < size && heap[right] < heap[smallest]) {smallest = right;}if (smallest != i) {swap(i, smallest);minHeapify(smallest);}}private int parent(int i) {return (i - 1) / 2;}private int leftChild(int i) {return 2 * i + 1;}private int rightChild(int i) {return 2 * i + 2;}private void swap(int i, int j) {int temp = heap[i];heap[i] = heap[j];heap[j] = temp;}
}
- 实现一个哈希表。
class MyHashMap {private final int SIZE = 10000;private ListNode[] table;class ListNode {int key;int value;ListNode next;public ListNode(int key, int value) {this.key = key;this.value = value;this.next = null;}}public MyHashMap() {table = new ListNode[SIZE];}public void put(int key, int value) {int index = getIndex(key);if (table[index] == null) {table[index] = new ListNode(-1, -1);}ListNode prev = findElement(table[index], key);if (prev.next == null) {prev.next = new ListNode(key, value);} else {prev.next.value = value;}}public int get(int key) {int index = getIndex(key);if (table[index] == null) {return -1;}ListNode prev = findElement(table[index], key);if (prev.next == null) {return -1;}return prev.next.value;}public void remove(int key) {int index = getIndex(key);if (table[index] == null) {return;}ListNode prev = findElement(table[index], key);if (prev.next == null) {return;}prev.next = prev.next.next;}private int getIndex(int key) {return Integer.hashCode(key) % SIZE;}private ListNode findElement(ListNode bucket, int key) {ListNode prev = null;ListNode curr = bucket;while (curr != null && curr.key != key) {prev = curr;curr = curr.next;}return prev;}
}
- 实现一个动态数组。
class DynamicArray {private int[] array;private int size;private int capacity;public DynamicArray() {array = new int[10];size = 0;capacity = 10;}public void add(int value) {if (size == capacity) {expandCapacity();}array[size] = value;size++;}public int get(int index) {if (index < 0 || index >= size) {throw new IndexOutOfBoundsException();}return array[index];}public void set(int index, int value) {if (index < 0 || index >= size) {throw new IndexOutOfBoundsException();}array[index] = value;}public int size() {return size;}public void remove(int index) {if (index < 0 || index >= size) {throw new IndexOutOfBoundsException();}for (int i = index; i < size - 1; i++) {array[i] = array[i + 1];}size--;}private void expandCapacity() {int newCapacity = capacity * 2;int[] newArray = new int[newCapacity];for (int i = 0; i < capacity; i++) {newArray[i] = array[i];}capacity = newCapacity;array = newArray;}
}
- 实现一个有序数组的二分查找。
class BinarySearch {public int search(int[] nums, int target) {int left = 0;int right = nums.length - 1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] == target) {return mid;} else if (nums[mid] < target) {left = mid + 1;} else {right = mid - 1;}}return -1;}
}
- 实现一个字符串的反转。
class StringReverse {public String reverse(String s) {char[] chars = s.toCharArray();int left = 0;int right = chars.length - 1;while (left < right) {char temp = chars[left];chars[left] = chars[right];chars[right] = temp;left++;right--;}return new String(chars);}
}
- 实现一个队列的使用两个栈来模拟。
class MyQueue {private Stack<Integer> inStack;private Stack<Integer> outStack;public MyQueue() {inStack = new Stack<>();outStack = new Stack<>();}public void push(int x) {inStack.push(x);}public int pop() {if (outStack.isEmpty()) {while (!inStack.isEmpty()) {outStack.push(inStack.pop());}}return outStack.pop();}public int peek() {if (outStack.isEmpty()) {while (!inStack.isEmpty()) {outStack.push(inStack.pop());}}return outStack.peek();}public boolean empty() {return inStack.isEmpty() && outStack.isEmpty();}
}
- 实现一个栈的使用两个队列来模拟。
class MyStack {private Queue<Integer> inQueue;private Queue<Integer> outQueue;public MyStack() {inQueue = new LinkedList<>();outQueue = new LinkedList<>();}public void push(int x) {inQueue.offer(x);while (!outQueue.isEmpty()) {inQueue.offer(outQueue.poll());}Queue<Integer> temp = inQueue;inQueue = outQueue;outQueue = temp;}public int pop() {return outQueue.poll();}public int top() {return outQueue.peek();}public boolean empty() {return outQueue.isEmpty();}
}
- 实现一个判断链表中是否有环的算法。
class ListNode {int val;ListNode next;public ListNode(int val) {this.val = val;this.next = null;}
}class LinkedListCycle {public boolean hasCycle(ListNode head) {ListNode slow = head;ListNode fast = head;while (fast != null && fast.next != null) {slow = slow.next;fast = fast.next.next;if (slow == fast) {return true;}}return false;}
}
内容来自

相关文章:

Java八股文(数据结构)
Java八股文の数据结构 数据结构 数据结构 请解释以下数据结构的概念:链表、栈、队列和树。 链表是一种线性数据结构,由节点组成,每个节点包含了指向下一个节点的指针; 栈是一种后进先出(LIFO)的数据结构&a…...
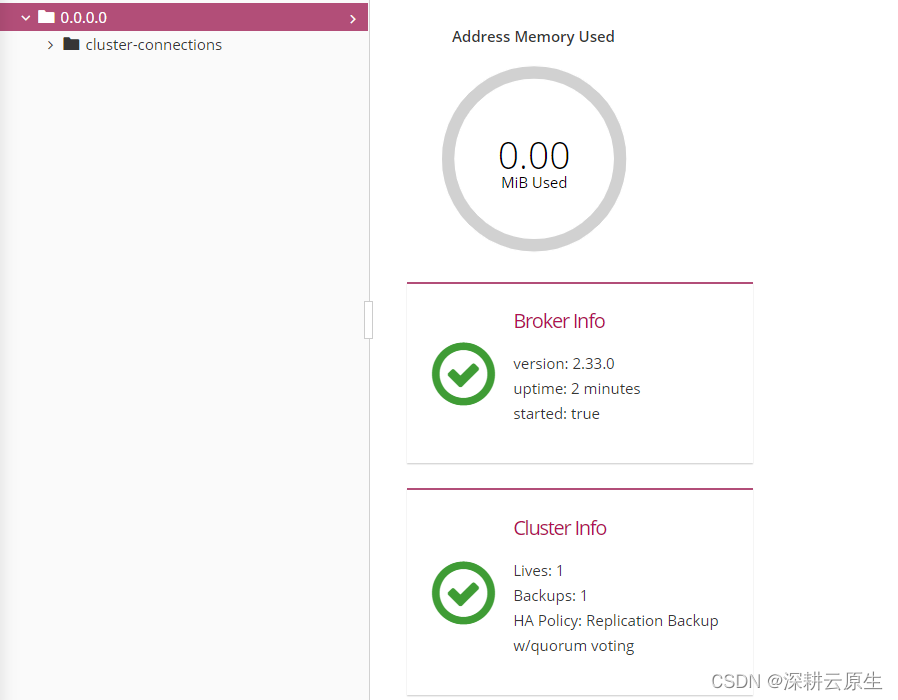
ActiveMQ Artemis 系列| High Availability 主备模式(消息复制) 版本2.19.1
一、ActiveMQ Artemis 介绍 Apache ActiveMQ Artemis 是一个高性能的开源消息代理,它完全符合 Java Message Service (JMS) 2.0 规范,并支持多种通信协议,包括 AMQP、MQTT、STOMP 和 OpenWire 等。ActiveMQ Artemis 由 Apache Software Foun…...

QGIS插件系列--WhiteBox Tools
WhiteBox Tools(官网机翻): WhiteboxTools是由圭尔夫大学地貌测量和水文地理信息学研究小组(GHRG)开发的高级地理空间软件包和数据分析平台。该项目始于2017年<>月,并在分析能力方面迅速发展。WhiteboxTools的一…...
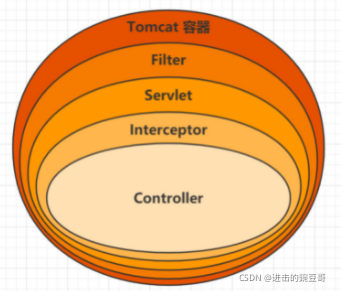
SpringMVC设置全局异常处理器
文章目录 背景分析使用ControllerAdvice(RestControllerAdvice)ExceptionHandler实现全局异常全局异常处理-多个处理器匹配顺序存在一个类中存在不同的类中 对于过滤器和拦截器中的异常,有两种思路可以考虑 背景 在项目中我们有需求做一个全…...

Acwing_795前缀和 【一维前缀和】+【模板】二维前缀和
Acwing_795前缀和 【一维前缀和】 题目: 代码: #include <bits/stdc.h> #define int long long #define INF 0X3f3f3f3f #define endl \n using namespace std; const int N 100010; int arr[N];int n,m; int l,r; signed main(){std::ios::s…...

docker 部署 gitlab-ce 16.9.1
文章目录 [toc]拉取 gitlab-ce 镜像创建 gitlab-ce 持久化目录启停脚本配置配置 gitlab-ce编辑 gitlab-ce 配置文件重启 gitlab-ce配置 root 密码 设置中文 gitlab/gitlab-ce(需要科学上网) 拉取 gitlab-ce 镜像 docker pull gitlab/gitlab-ce:16.9.1-ce.0查看镜像是不是有 Vo…...

29.Python从入门到精通—Python3 面向对象继承 多继承 方法重写 类属性与方法
29.从入门到精通:Python3 面向对象继承 多继承 方法重写 类属性与方法 继承多继承方法重写类属性与方法 继承 在面向对象编程中,继承是指通过继承现有类的属性和方法来创建新类的过程。新类称为子类(或派生类),现有类…...

jQuery如何获取元素宽高?
在jQuery中,获取元素的宽和高有多种方法,取决于你是否需要包括边框、内边距或其他额外空间。以下是几种常用的方式: 获取元素内容区域的宽和高(不包括边框和内边距): var width $(#yourElement).width(); …...
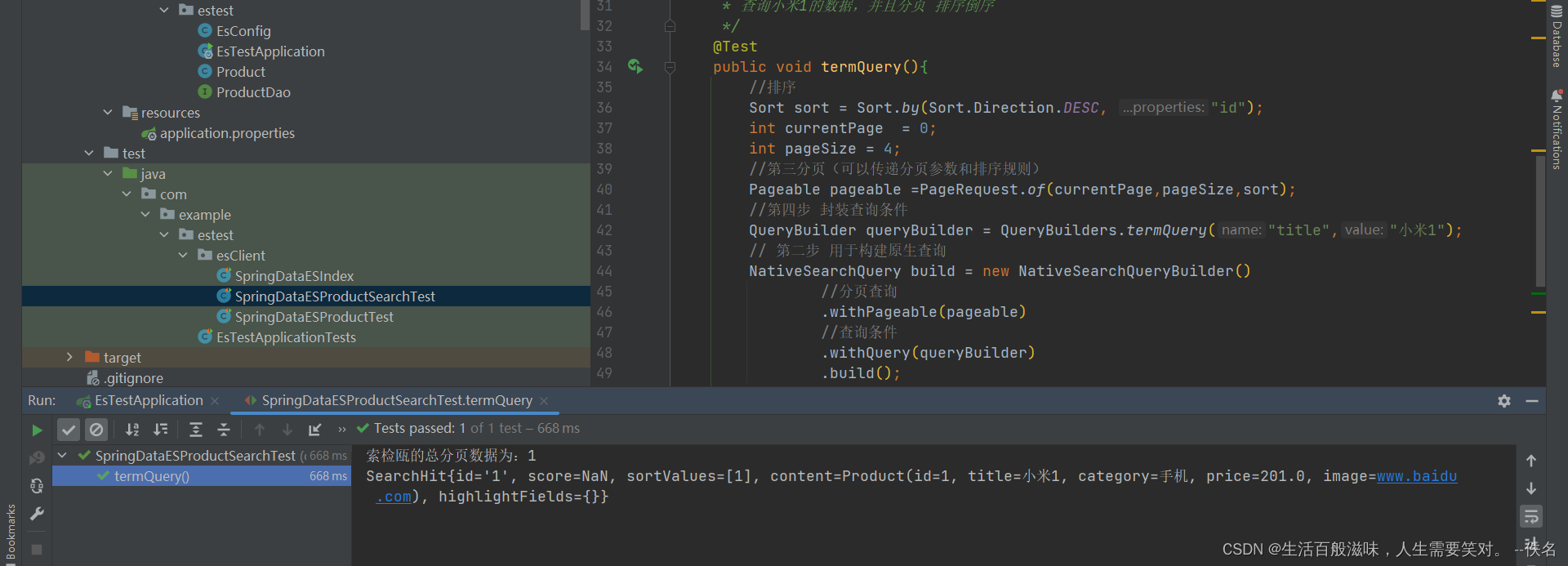
springdata框架对es集成
什么是spring data框架 Spring Data是一个用于简化数据库、非关系型数据库、索引库访问,并支持云服务的开源框架。其主要目标是使得对数据的访问变得方便快捷,并支持 map-reduce框架和云计算数据服务。Spring Data可以极大的简化JPA(Elasticsearch…)的…...
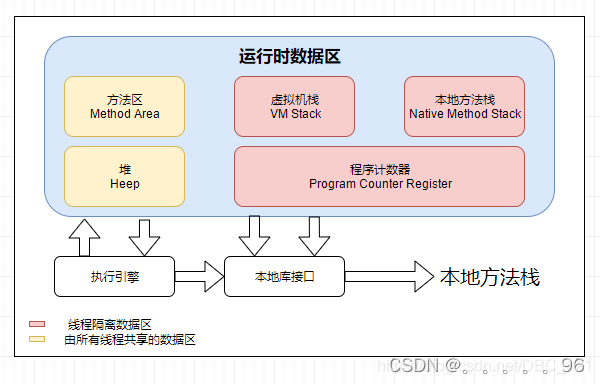
jvm(虚拟机)运行时数据区域介绍
Java虚拟机(JVM)运行时数据区域是Java程序在运行过程中使用的内存区域,它主要包括以下几个部分: 程序计数器(Program Counter Register): 程序计数器是一块较小的内存区域,是线程私有…...
)
C++ MFC 只启动一个程序实例 唤醒之前的实例(完整源码)
初级代码游戏的专栏介绍与文章目录-CSDN博客 很多时候我们希望只允许启动一个程序实例,如果再次运行,就唤醒之前的实例。 目录 1 概述 2 相关技术介绍 2.1 互斥对象 2.2 查找窗口 2.3 唤醒窗口 1 概述 技术上并不难,涉及到以下几个技术…...

2024多云管理平台CMP排名看这里!
随着云计算技术的迅猛发展,多云管理平台CMP应运而生。多云管理平台CMP仅能够简化对多个云环境的统一管理,还能提高资源利用效率和降低成本。因此了解多云管理平台CMP品牌是必要的。2024多云管理平台CMP排名看这里!仅供参考哈! 20…...

MySQL 数据库的日志管理、备份与恢复
一. 数据库备份 1.数据备份的重要性 备份的主要目的是灾难恢复。 在生产环境中,数据的安全性至关重要。 任何数据的丢失都可能产生严重的后果。 造成数据丢失的原因: 程序错误人为,操作错误,运算错误,磁盘故障灾难(如火灾、地震࿰…...
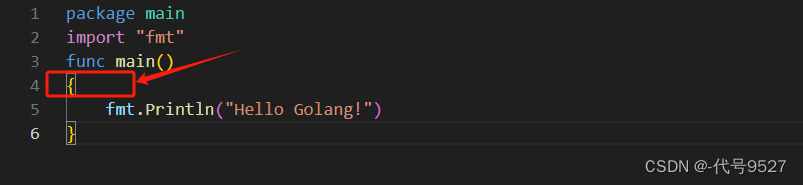
一、Go开发环境搭建
文章目录 1、开发工具2、开发环境配置3、Hello World4、语法 1、开发工具 https://code.visualstudio.com/download 2、开发环境配置 类比Java的JDK,go的SDK下载:https://studygolang.com/dl 解压: 配置环境变量path,将命令&quo…...
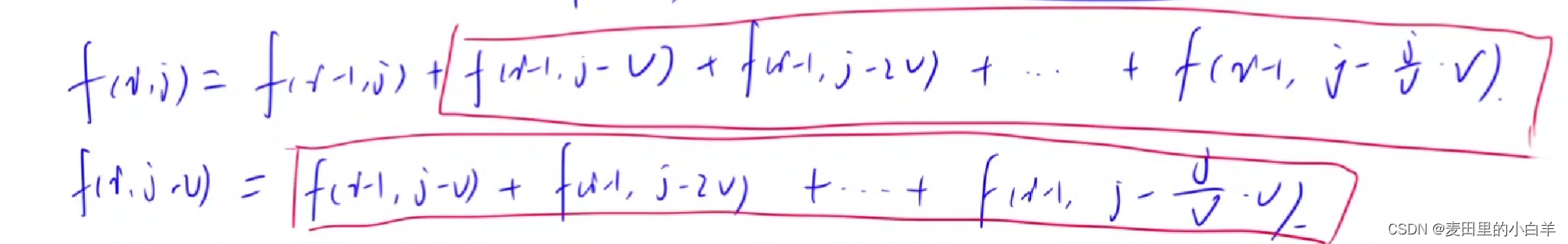
包子凑数(蓝桥杯,闫氏DP分析法)
题目描述: 小明几乎每天早晨都会在一家包子铺吃早餐。 他发现这家包子铺有 N 种蒸笼,其中第 i 种蒸笼恰好能放 Ai 个包子。 每种蒸笼都有非常多笼,可以认为是无限笼。 每当有顾客想买 X 个包子,卖包子的大叔就会迅速选出若干笼…...

Java八股文(JVM)
Java八股文のJVM JVM JVM 什么是Java虚拟机(JVM)? Java虚拟机是一个运行Java字节码的虚拟机。 它负责将Java程序翻译成机器代码并执行。 JVM的主要组成部分是什么? JVM包括以下组件: ● 类加载器(ClassLoa…...

云硬盘扩容后将空间增加到原有分区的解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的…...
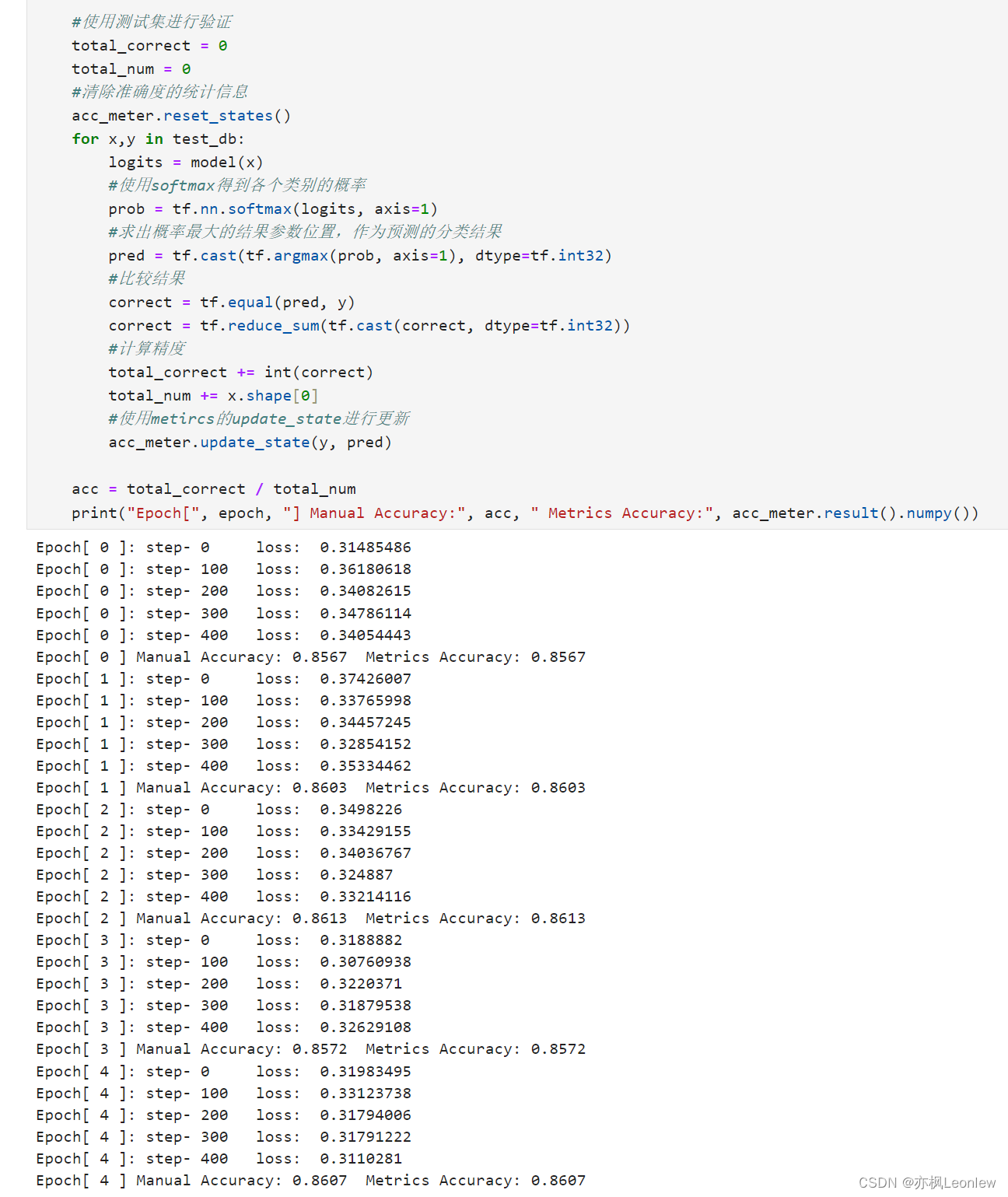
Tensorflow2.0笔记 - metrics做损失和准确度信息度量
本笔记主要记录metrics相关的内容,详细内容请参考代码注释,代码本身只使用了Accuracy和Mean。本节的代码基于上篇笔记FashionMnist的代码经过简单修改而来,上篇笔记链接如下: Tensorflow2.0笔记 - FashionMnist数据集训练-CSDN博…...

LeetCode 面试经典150题 290.单词规律
题目: 给定一种规律 pattern 和一个字符串 s ,判断 s 是否遵循相同的规律。 这里的 遵循 指完全匹配,例如, pattern 里的每个字母和字符串 s 中的每个非空单词之间存在着双向连接的对应规律。 思路:一一映射需要用到…...
)
【CASS精品教程】CASS中计算四参数和七参数(以RTK数据为例)
文章目录 一、四参数介绍二、四参数计算三、七参数介绍四、四参数、七参数的区别一、四参数介绍 两个不同的二维平面直角坐标系之间转换通常使用四参数模型,四参数适合小范围测区的空间坐标转换,相对于七参数转换的优势在于只需要2个公共已知点就能进行转换,操作简单。 在…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
