【每日力扣】343. 整数拆分与63. 不同路径 II

🔥 个人主页: 黑洞晓威
😀你不必等到非常厉害,才敢开始,你需要开始,才会变的非常厉害
343. 整数拆分
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
解题思路
这个问题可以使用动态规划来解决。我们定义一个数组 dp,其中 dp[i] 表示将正整数 i 拆分后可以获得的最大乘积。
首先,我们初始化 dp[1] = 1,因为任何数拆分成两个数的乘积最小值为 1 * 1 = 1。
然后,我们从正整数 2 开始,依次计算 dp 数组的值。对于每个正整数 i,我们通过迭代 j(j 的范围是从 1 到 i - 1)来计算 dp[i]。对于每个 j,我们计算两种情况下的最大值:
- j * (i - j):将 i 拆分成 j 和 i - j 两个数相乘的结果。
- j * dp[i - j]:将 i 拆分成 j 和 dp[i - j] 两个数相乘的结果。
代码实现
class Solution {public int integerBreak(int n) {int[] dp = new int[n + 1];dp[1] = 1; // 初始化 dp[1]for (int i = 2; i <= n; i++) {for (int j = 1; j < i; j++) {dp[i] = Math.max(dp[i], Math.max(j * (i - j), j * dp[i - j]));}}return dp[n];}
}63. 不同路径 II
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示
解题思路
我们可以定义一个二维数组 dp,其中 dp[i][j] 表示从起始点到达网格的位置 (i, j) 的不同路径数。根据题目要求,如果某个位置有障碍物,那么该位置的路径数为 0。
接下来,我们可以根据动态规划的状态转移方程来计算 dp 数组。状态转移方程如下:
- 如果当前位置 (i, j) 是障碍物(obstacleGrid[i][j] == 1),那么 dp[i][j] = 0;
- 否则,dp[i][j] = dp[i-1][j] + dp[i][j-1],即当前位置的路径数等于上方和左方位置的路径数之和。
最终,dp[m-1][n-1] 即为从起始点到达右下角的不同路径数。
代码实现
class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int m = obstacleGrid.length;int n = obstacleGrid[0].length;int[][] dp = new int[m][n];// 初始化起始点dp[0][0] = obstacleGrid[0][0] == 1 ? 0 : 1;// 初始化第一列for (int i = 1; i < m; i++) {dp[i][0] = obstacleGrid[i][0] == 1 ? 0 : dp[i-1][0];}// 初始化第一行for (int j = 1; j < n; j++) {dp[0][j] = obstacleGrid[0][j] == 1 ? 0 : dp[0][j-1];}// 计算其余位置的路径数for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = obstacleGrid[i][j] == 1 ? 0 : dp[i-1][j] + dp[i][j-1];}}return dp[m-1][n-1];}
}相关文章:

【每日力扣】343. 整数拆分与63. 不同路径 II
🔥 个人主页: 黑洞晓威 😀你不必等到非常厉害,才敢开始,你需要开始,才会变的非常厉害 343. 整数拆分 给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k > 2 ),并使…...

洛谷 Cut Ribbon
思路:我们可以看出,这是一道完全背包问题,但是呢,有一点需要注意:那就是我们在装背包的时候并不能保证一定能装满背包,但是这里的背包要求是让我们装满的,所以我们需要判断这个背包装满才行&…...

#AS,idea,maven,gradle
Jdk,sdk。提前都是需要下好的。 Maven与gradle的思考: 用AS开发app时,gradle本就有,自己也可以指定,AGP同样。要注意gradle,AGP,jdk版本的事情。还有依赖库。 用idea开发网络程序时,也有内置的maven&…...
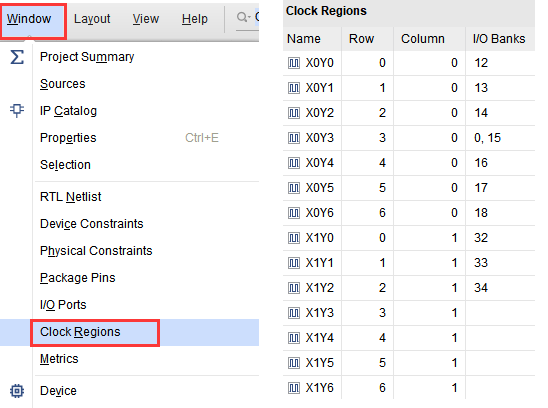
FPGA结构与片上资源
文章目录 0.总览1.可配置逻辑块CLB1.1 6输入查找表(LUT6)1.2 选择器(MUX)1.3 进位链(Carry Chain)1.4 触发器(Flip-Flop) 2.可编程I/O单元2.1 I/O物理级2.2 I/O逻辑级 3.布线资源4.其…...

【分布式】——分布式事务
分布式事务 ⭐⭐⭐⭐⭐⭐ Github主页👉https://github.com/A-BigTree 笔记链接👉https://github.com/A-BigTree/tree-learning-notes ⭐⭐⭐⭐⭐⭐ Spring专栏👉https://blog.csdn.net/weixin_53580595/category_12279588.html SpringMVC专…...

第6章:“让我们思考这个”的提示
“让我们思考这个”这一提示词,是深度对话的钥匙,鼓励ChatGPT生成反思性、沉思性的文本。 对于论文写作、诗歌创作或创意任务的完成,非常实用。 当你想要深究某主题时,只需向ChatGPT提问。 它会基于提示,结合算法和…...

安卓Activity上滑关闭效果实现
最近在做一个屏保功能,需要支持如图的上滑关闭功能。 因为屏保是可以左右滑动切换的,内部是一个viewpager 做这个效果的时候,关键就是要注意外层拦截触摸事件时,需要有条件的拦截,不能影响到内部viewpager的滑动处理…...

使用conda管理python环境
为什么需要管理环境? 每个python程序依赖的库版本可能不同,因此我们需要隔离不同的环境。 创建环境: conda create --name myenv python3.8这将创建一个名为myenv的新环境,并在其中安装Python 3.8版本。 列出所有环境…...

MR混合现实情景实训教学系统在军事演练课堂中的教学应用
MR混合现实情景实训教学系统在军事演练课堂中的教学应用具有以下优势: 1. 增强现实感:通过MR技术,学生可以在军事演练中更真实地感受到战场环境,增强他们的实战经验。 2. 提高训练效率:通过MR技术,可以模…...

vant checkbox 复选框 样式改写
修改前 修改后 基于 vant: 4.8.3 unocss: 0.53.4 <van-checkbox-group v-model"query.zczb" shape"square" class"text-16 w-100% flex flex-wrap"><template v-for"item in registerCapitalOption"><v…...
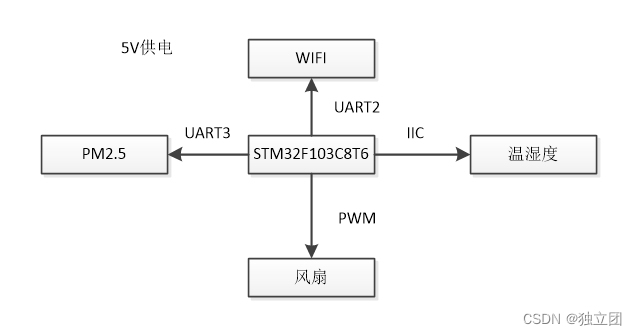
物联网实战--入门篇之(一)物联网概述
目录 一、前言 二、知识梳理 三、项目体验 四、项目分解 一、前言 近几年很多学校开设了物联网专业,但是确却地讲,物联网属于一个领域,包含了很多的专业或者说技能树,例如计算机、电子设计、传感器、单片机、网…...

将yolov5s部署到安卓上实战经验总结
最近需要在手机端实现一个目标检测的功能,于是选择了小巧又在目标检测方面表现很好的yolov5s,官网下载yolov5代码,用自己做的数据集进行了训练,然后把模型转换成torchscript格式,这些过程网上都有很多讲解,…...
)
算法日记————对顶堆(4道题)
对顶堆的作用主要在于动态维护第k大的数字,考虑使用两个优先队列,一个大9999999999根堆一个小根堆,小根堆维护大于等于第k大的数字的数,它的堆顶就是堆内最小,第k大的数字,另外一个大根堆维护小于等于k的数…...
【I.MX6ULL移植】Ubuntu-base根文件系统移植
1.下载Ubuntu16.04根文件系统 http://cdimage.ubuntu.com/ 1 2 3 4 5 2.解压ubuntu base 根文件系统 为了存放 ubuntu base 根文件系统,先在 PC 的 Ubuntu 系统中的 nfs 目录下创建一个名为 ubuntu_rootfs 的目录,命令如下: 【注意&…...

unity3d for web
时光噶然 一晃好多年过去了(干了5年的u3d游戏),记得最后一次使用的版本好像是 unity 2017。 那个是 unity3d for webgl 还需要装个插件。用起来很蛋疼。 最近做一个小项目 在选择是用 Layabox 还是 cocosCreate 的时候 我想起了老战友 Uni…...
关于消费者研究的流程)
大宋咨询(深圳问卷调研)关于消费者研究的流程
消费者研究是一项至关重要的任务,它有助于企业了解目标市场的需求、偏好和行为,从而制定更加精准的营销策略。在执行消费者研究时,需要遵循一定的步骤和方法,以确保研究的准确性和有效性。开展消费者研究需要一系列的步骤和方法。…...

STM32看似无法唤醒的一种异常现象分析
1. 引言 STM32 G0 系列产品具有丰富的外设和强大的处理性能以及良好的低功耗特性,被广泛用于各类工业产品中,包括一些需要低功耗需求的应用。 2. 问题描述 用户使用 STM32G0B1 作为汽车多媒体音响控制器的控制芯片,用来作为收音机频道存贮…...
iOS - Runtime-isa详解(位域、union(共用体)、位运算)
文章目录 iOS - Runtime-isa详解(位域、union(共用体)、位运算)前言1. 位域介绍1.1 思路1.2 示例 - 结构体1.3 示例 - union(共用体)1.3.1 说明 1.4 结构体 对比 union(共用体) 2. a…...

使用VSCode搭建Vue 3开发环境
使用VSCode搭建Vue 3开发环境 Vue 3是一种流行的前端JavaScript框架,它提供了响应式的数据绑定和组合式的API。Visual Studio Code(VSCode)是一个轻量级但功能强大的源代码编辑器,支持多种语言开发。本文将引导您完成使用VSCode搭建Vue 3开发环境的步骤。 1. 下载和安装V…...
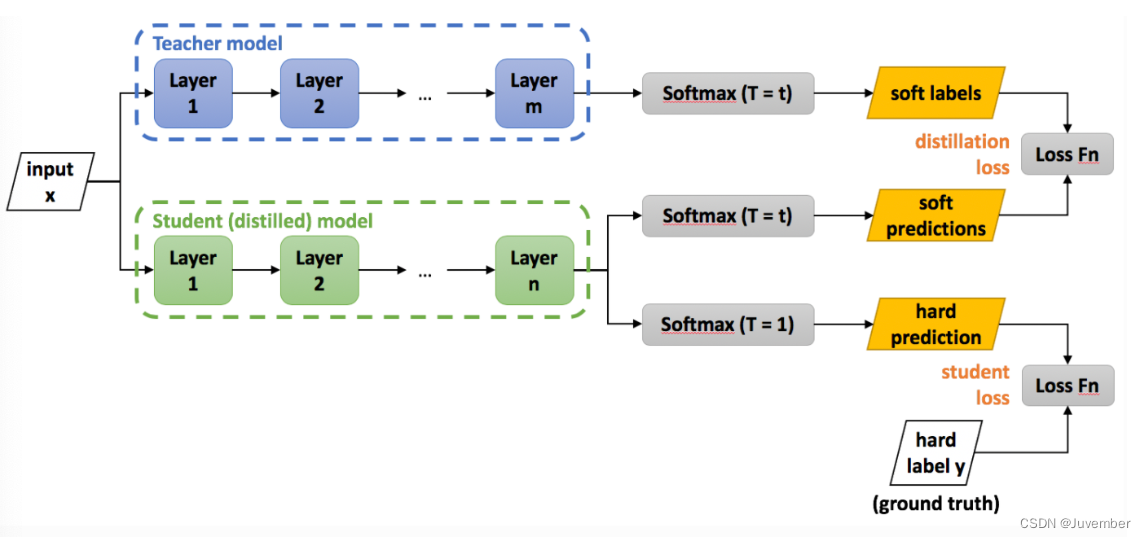
深度学习中的模型蒸馏技术:实现流程、作用及实践案例
在深度学习领域,模型压缩与部署是一项重要的研究课题,而模型蒸馏便是其中一种有效的方法。 模型蒸馏(Model Distillation)最初由Hinton等人在2015年提出,其核心思想是通过知识迁移的方式,将一个复杂的大模型…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...
